基于UDEC节理岩体抗压强度的数值研究
鲁皓琰,栗东平*,钟江城,李 冲
(1.河北工程大学 土木工程学院,河北 邯郸 056038;2.河北工程大学 计算力学与工程应用研究中心,河北 邯郸 056038;3.中国矿业大学(北京) 力学与建筑工程学院,北京 100083)
岩体失稳、煤矿塌方、瓦斯突出等事故均受岩体节理面特征的影响[1]。确定节理岩体的表征单元体,研究其各向异性一直是岩石力学领域研究的重点问题[2]。节理岩体强度原位试验具有难度大、周期长、费用高、结果离散性大等特点。近年来,国内外学者从理论分析、实验研究、数值模拟等方面对岩体的各向异性进行了研究[3-22]。在节理岩体网络反演、岩体力学参数的尺寸效应、节理对岩体力学参数的影响等多个方面取得了一定的成果。目前,通过现场实测还难以生成岩体节理网络,只能通过量测岩体表面节理网络统计得到其平面或三维的节理网络,即使统计生成的等效三维节理网络也不能完全反映实际的节理岩体,又鉴于节理分布的复杂性和节理岩体三维网络图反演的不确定性、节理网络提取的复杂性及实验手段的局限性等诸多因素,因此本文采用节理岩体平面裂隙网络图开展研究。研究表明节理分布、长度、间距等几何参数均符合分形特征,可基于分形理论反演岩体的节理网络,即通过可测的、小范围的岩体节理去推求不可测的、更大范围的各向异性节理岩体网络。本文基于分形理论,结合Monte Carlo方法生成节理岩体网络图,以网络图中心为基点,选取节理岩体模拟试件,通过岩石力学试验和Hoek-Brown准则获取岩体的力学参数。在此基础上,利用UDEC开展不同围压、不同尺寸、不同取样角度节理岩体的抗压强度数值实验,研究节理岩体的各向异性。
1 试验过程
1.1 试件制备
试验岩石试样取自江西某矿区,根据《工程岩体试验方法规程》要求,先采用ZS-100型岩石钻孔机进行岩石的钻心取样,再加工成尺寸为50 mm×100 mm的标准圆柱体试件,如图1所示。

图1 岩石试件
1.2 试验操作
利用TAW-2000型微机控制电液伺服岩石三轴试验机进行试验,获取岩石试件的单轴抗压强度、轴向压缩应变、径向压缩应变及其三轴抗压强度。根据《工程岩体试验方法规程》整理试验数据,得到岩石试件的物理力学参数,包括天然密度,单轴抗压强度,围压为5、10、15、20 MPa时的抗压强度等。
1.3 试验结果
1.3.1 密度试验结果
岩石密度采用量积法,试验结果如表1所示。
1.3.2 岩石单轴压缩试验结果
计算岩石的弹性模量与泊松比[23]。弹性模量E计算如式(1)所示。
E=σc(50)/εh(50)
(1)
式中,σc(50)为试件单轴抗压强度的50%(MPa);εh(50)为σc(50)处对应的轴向压缩应变;E为试件弹性模量(GPa)。
泊松比μ计算如式(2)所示。
μ=εd(50)/εh(50)
(2)
式中,εd(50)为σc(50)处对应的径向压缩应变;εh(50)为σc(50)处对应的轴向压缩应变;μ为泊松比。
弹性模量E及泊松比μ计算结果如表2所示。
1.3.3 岩石三轴压缩变形试验结果
试验初始阶段,以0.05 MPa/s速率同时将围压和轴向荷载增加至预定值,将此时试件的轴向压缩变形值作为初始值,稳定后将轴向荷载速率提升至0.08 MPa/s,直至试件破坏。利用莫尔-库伦强度准则计算抗剪强度参数(内摩擦角φ、粘聚力c)。结果如表3所示。

表1 岩石天然密度试验

表2 岩石单轴压缩变形

表3 岩石三轴试验结果
2 Hoek-Brown法确定岩体力学参数
上世纪末Hoek和Brown等修正了地质强度指标GSI,并对大量的岩体现场实验结果进行研究,总结出狭义Hoek-Brown强度准则。之后,Hoek等[3-4]引入岩体扰动系数D(根据扰动程度取值范围为0~1),并通过对三轴试验数据以及岩体内部构造的综合分析,提出了广义Hoek-Brown强度准则。
(3)
(4)
(5)
(6)
式中,σ1′—岩石破坏时最大有效主应力(MPa);σ3′—岩石破坏时最小有效主应力(MPa);σci—岩石单轴抗压强度(MPa);mb,s,a—Hoek-Brown常数。mi为岩石材料常数,可以通过三轴实验获得。令X=σ3,Y=(σ1-σ3)2,mi计算公式如式(7)所示。
(7)
岩体的摩擦角φ、等效粘聚力c值可通过式(8)、式(9)求出。
(8)
(9)

岩体变形模量Em采用式(10)计算。式中,Ei为实验室完整岩块弹性模量(GPa)。
(10)
由式(11)、(12)可计算得到用于数值模拟的岩体剪切模量G与体积模量K。
(11)
(12)
3 数值模型的建立
基于分形理论,采用C++Builder语言编写岩体节理网络程序,输入节理中点聚集维数Dc、节理长度维数DL、节理平均长度、最大节理数、最长节理数、节理倾角及变化幅值、分盒次数等参数,生成节理岩体网络图。以生成的节理岩体中心为基点选取数值实验试件,高宽之比为2,试件尺寸由大到小依次取:4.8 m×9.6 m、2.4 m×4.8 m、1.2 m×2.4 m、0.6 m×1.2 m、0.3 m×0.6 m,取样角度为30°、60°、90°、120°、150°。取样角度为30°时,各尺寸数值实验试件选取如图2所示。

图2 数值实验试件选取(取样角度为30°)
在数值模拟之前,需对数值实验试件进行一定程度的调整,以保证软件的运算速度。如:若节理大部分与岩体边界接近,则将其移至边界;若节理长度过小,则将其删除;若两条节理十分接近且长度、方向大体一致,则将其合为一条。
离散元软件UDEC要求不连续结构面必须贯通岩体上下或左右边界,否则将自动删除结构面。而删除大量的非贯通节理面无疑会降低模拟结果的准确度。因此,常采用人为搭接的方式,使这些结构面得以贯通,搭接的原则是尽可能的精简。人为搭接部分称为虚拟节理面,虚拟节理面参数的选取应尽量与岩体自身力学参数近似,具体选取方法参考文献[2]。
4 数值试验
4.1 参数选取
基于室内岩石力学试验结果,根据公式(3)—(12),利用Hoek-Brown准则估算岩体力学参数,结果如表4所示,数值实验岩体力学参数设置时采用该估算值。选取节理面力学参数[24],如表5所示。
4.2 数值实验
通过UDEC离散元程序,建立不同取样角度、不同尺寸的25个数值计算模型,岩体力学参数和节理面力学参数如表4、表5所示。围压σ3分别取0、2、4、6、8 MPa,采用速率加载方式实现荷载施加,得到各个试块的抗压强度值。图3为典型的抗压强度曲线及应力云图。

表5 节理计算参数
5 数值试验结果分析
根据数值实验得到不同尺寸、不同围压、不同取样角度下岩体的抗压强度值,如表6所示。

表6 节理岩体强度的数值模拟结果

表4 岩体力学参数估算结果

图3 典型的抗压强度曲线及应力云图
5.1 取样角度对岩体抗压强度的影响
岩体抗压强度随取样角度变化关系如图4所示。由表6、图4(a)不难看出,尺寸为0.3 m×0.6 m的试件当取样角度介于30°到150°时,岩体的抗压强度呈现较为明显的波动,其波动规律为先上升后下降最后再上升,在取样角度为60°左右时抗压强度达到峰值,在60°~120°段有一个明显的下降过程,并且在120°之后会有进一步的提高。其规律不同于单组节理的“U”趋势,这也说明节理分布是引起抗压强度各向异性的重要原因。
其他几组尺寸的节理岩体抗压强度随取样角度的变化规律基本一致,随着尺寸的增大,试件的抗压强度趋近于岩体的抗压强度,当取样角度介于30°到150°时,岩体的抗压强度呈现较为微弱的波动,波动规律为先上升后下降最后再上升。同样,当取样角度位于60°左右时岩体的抗压强度达到最高值,与尺寸为0.3 m×0.6 m的小体积岩体类似,与文献[22]岩体各向异性数值试验结论大体一致。这是由于随着尺寸的增大,节理数目、节理倾角和长度等分形特征愈加明显,造成了抗压强度随取样角度变化规律的波动性减缓。抗压强度随取样角度的典型变化关系如图4(b)所示。

图4 岩体抗压强度随取样角度的变化关系
图5为2、4 MPa围压下,不同尺寸岩体峰值应力σ1与第三主应力σ3比值随岩体取样角度变化规律。可以看出在岩体尺寸为0.3 m×0.6 m时,岩体抗压强度较大,曲线波动变化明显,σ1/σ3值随节理岩体取样角度增大,呈先增大、后减小、最后趋于平缓的趋势,在接近于60°时达到最高。随着岩体尺寸的增大,σ1/σ3值逐级减小,且σ1/σ3值随取样角度变化的波动幅度趋于平缓,各向异性趋于不明显。其余围压下不同尺寸岩体σ1/σ3值随岩体取样角度变化走势与图5类似。再次验证了图4得到的岩体抗压强度随取样角度的变化规律。
5.2 节理岩体抗压强度随围压的变化规律
由表6可观察到,随着围压的增大,节理岩体抗压强度也随之增大。图6是典型的岩体抗压强度随围压变化拟合曲线。显然,随着围压的增大,岩体抗压强度呈线性增长,且线性关系明显,如式(13)所示。
σ1=a+bσ3
(13)
式中,σ1为抗压强度,单位为MPa;σ3为围压,单位为MPa;a、b为拟合系数。
当试件尺寸为0.3 m×0.6 m时,抗压强度随围压线性变化斜率较高,各取样角度岩体斜率在5.0以上,并且随着选取角度的增大,节理岩体抗压强度随围压增大的增幅呈明显减小趋势;当试件尺寸较大时,抗压强度随围压线性变化斜率较低,各尺寸各取样角度岩体斜率在2.0~3.0之间,并且随着选取角度的增大,节理岩体抗压强度随围压增大的增幅呈波动变化,但波动幅度不大,这与试件尺寸较大时,节理分布分形特征明显有关。各尺寸岩体抗压强度随围压拟合式在60°取样时斜率最大,围压效应最为明显。选取角度一定,随着节理岩体尺寸的增大,岩体抗压强度随围压增大的增幅减小,这也说明随着岩体尺寸的增大,围压效应减弱,节理岩体的各向异性趋于不明显。

图6 岩体抗压强度随围压的变化关系
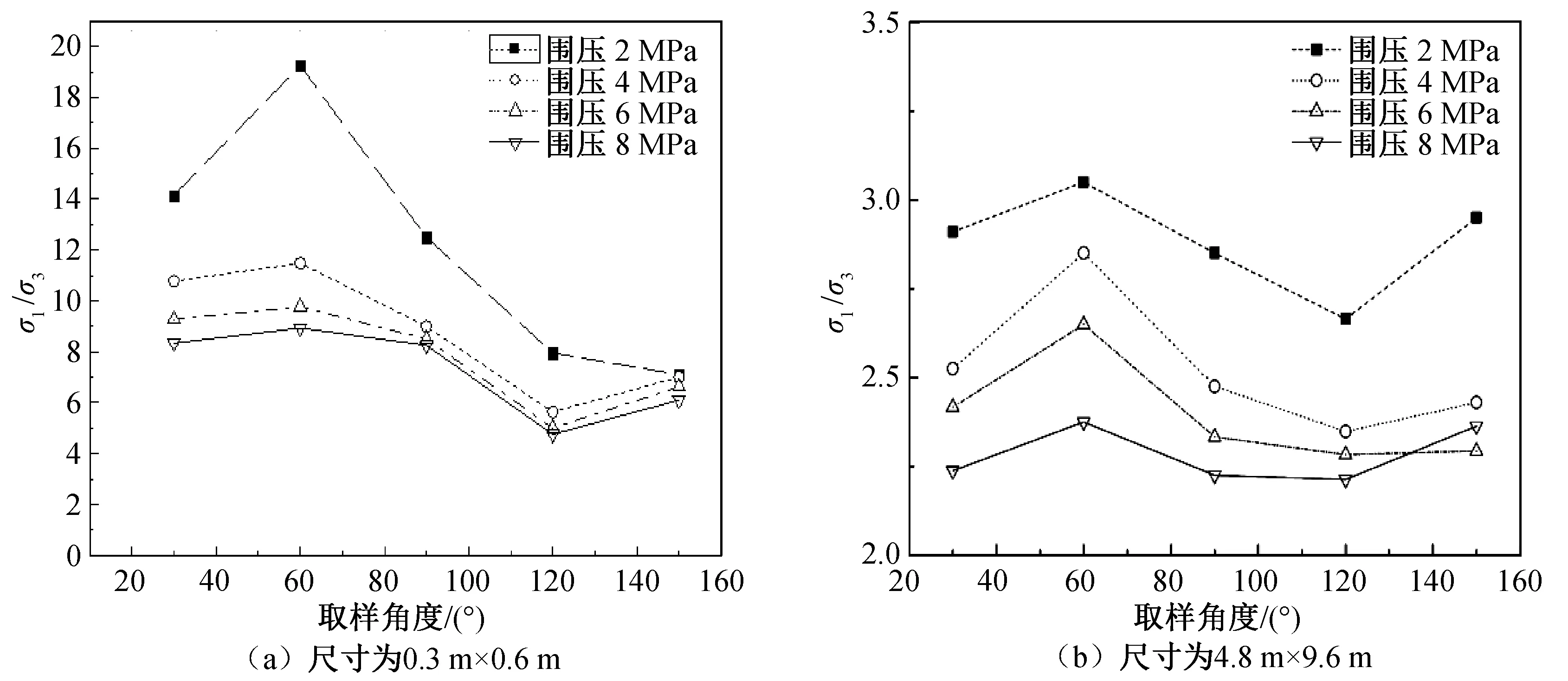
图7 各尺寸岩体不同围压下σ1/σ3随岩体取样角度的变化曲线
图7为不同围压下峰值应力σ1与第三主应力σ3随取样角度的典型变化关系。显然,节理岩体尺寸为0.3 m×0.6 m且围压一定时,σ1/σ3的值在30°~60°段呈现明显的上升,在60°~90°段呈明显的下降,90°~150°段呈波动趋势。不同围压下,取样角度为60°时σ1/σ3的值最大,且随着围压的增大,σ1/σ3值逐渐减小,说明围压的增大使得岩体的各向异性趋于不明显。随着岩体尺寸的增大,当围压一定时,σ1/σ3的值随节理岩体取样角度的波动趋势与图7基本一致,但由于岩体尺寸的增加,抗压强度值变小,波动趋势趋于平缓。
5.3 节理岩体抗压强度随尺寸的变化规律
相同选取角度、相同围压下,随着岩体尺度的增大,试件的抗压强度逐渐减小,当试件长度增大至1.2 m时抗压强度下降幅度最大,之后逐渐趋于稳定。图8为典型的岩体抗压强度随尺寸变化的拟合关系,负指数关系明显,如式(14)所示。
σ1=σ0+αe-β(L-γ)
(14)
式中,σ1为节理岩体抗压强度,单位为MPa;L为试件尺寸,单位为m;σ0、α、β、γ为拟合系数。γ代表岩石表征尺度,对比各个取样角度的岩体不难发现,岩体的表征单元体受取样角度影响不大,各个方向的表征单元体尺度基本上都趋于某个定值,随着尺度的增大,可忽略其对岩体强度的影响。α代表岩石抗压强度与岩体抗压强度差值,随围压的增大而增大,这也充分说明了岩石强度不可等价于岩体强度。β可以看作是抗压强度的一个重要影响因子,为无量纲力学变量,与施加的围压、节理分布等要素有关。不同取样角度的岩体尺寸效应拟合系数如表7所示。

图8 不同取样角度岩体抗压强度随岩体尺寸的变化关系

表7 岩体抗压强度尺寸效应的拟合系数
6 结论
1)围压、尺寸相同时,随着选取角度的增大,节理岩体抗压强度呈微幅波动变化趋势,波动规律为先上升后下降最后再上升,取样角度为60°时强度值略高,且抗压强度的尺寸效应与围压效应较为明显,这应与节理分布的分形特性有关。
2)选取角度、尺寸相同时,随着围压的增大,节理岩体抗压强度呈线性增大趋势,随着岩体尺寸的增大,各选取角度间的σ1/σ3波动幅度会降低,围压对其抗压强度的影响减弱,节理岩体的各向异性也趋于不明显。
3)选取角度、围压相同时,随着岩体尺寸的增大,节理岩体抗压强度呈非线性减小趋势,并趋向于某一定值,可拟合为负指数变化关系,揭示了节理岩体的各向异性。

