基于随机蛙跳和支持向量机的冬小麦叶面积指数估算

孙晶京，杨武德，冯美臣，肖璐洁

（1.山西农业大学 农学院，山西 太谷030801；2.山西农业大学 文理学院，山西 太谷030801）

叶面积指数（LAI）不仅是表征植被光合面积和冠层结构的重要参数，而且与植被的许多生物和物理过程密切相关［1］，了解农作物的LAI 及其动态变化对于作物水肥调节、长势监测和作物产量估算等具有一定意义［2，3］。传统测量LAI 的方法费时费力成本偏高，且仅限于实验田实地测量。高光谱遥感由于具有波段的连续性，光谱信息量大以及快速、无损和大范围监测的特点，被认为是估算LAI 的有力工具［4～9］。

近年来，利用高光谱遥感数据进行LAI 估算的方法被广泛使用。Wang 等［10］表明，红边波段和短波近红外波段（766 nm 和830 nm）的组合以及长波近红外波段（1 114 nm 和1 190 nm）的组合对于产生窄带NDVI 是最佳的。Feng 等［11］利用728 nm和798 nm 处的反射率构造了一种新的优化非线性植被指数，并证明该指数在冬小麦LAI 预测方面表 现 出 优 异 的 性 能。Xie 等［12］利 用735 nm 和736 nm 处的反射率对土壤调整植被指数进行改进，结果表明，当使用地面光谱时，改进后指数可以得到最佳的LAI 估算。梁栋等［13］利用光谱小波变换系数与LAI 做相关分析，得出利用变换后的小波系数能更好地筛选出对LAI 敏感的波段。但利用植被指数构建的LAI 预测模型没有充分利用高光谱的光谱信息，且不足以进行非线性解释。基于LAI 和原始或转换后的高光谱数据之间的相关系数的方法虽已被证明能够提取更多敏感波段并提高LAI 模型预测精度，但仍不能有效地消除已提取特征波段之间的冗余。而基于加权系数回归的波段选择方法［14，15］，不仅能有效地剔除与研究对象属性不相关的光谱波段，而且能改善模型预测能力和增强模型的鲁棒性。随机蛙跳算法就是其中一种优秀的变量选择算法，它借鉴了可逆跳马尔可夫链蒙特卡洛（RJMCMC）技术的优点，可以在不同模型之间以固定维或跨维方式转移，实现了对模型空间的搜索。由于随机蛙跳算法具有强大的模型搜索能力，本文旨在探讨其在冬小麦高光谱特征提取中的最佳应用模式。

1 材料和方法

1.1 研究区域

试验于2016 年10 月-2017 年6 月在山西省闻喜 县（110°59′33″～111°37′29E，35°9′38″～35°34′11″N）进行，该区域属于温带大陆性季风气候，海拔400～800 m，年平均气温在10～14 ℃之间，年平均降水量为500～650 mm，无霜期为160～220 d。在全县范围内选择17 个冬小麦采样点，其中7 个为旱地，其它为水浇地。在不同生育期对每个采样点进行数据采集，包括冠层光谱反射率和收集小麦叶片。

1.2 数据采集

冠层光谱使用ASD Fieldspec3 高光谱辐射仪（美国ASD 公司）测量。选择在晴朗无风的条件下进行，时间：10：00am～14：00pm（北京时区）。测量时探头垂直向下，并位于小麦冠层上方约0.5 m处。测量前后，用40 cm×40 cm BaSO4标准板校正。每个采样点重复10 次，取其平均值作为该采样点的光谱测量值。为避免大气水对吸收波段的影响，将位于1 350～1 480 nm、1 780～1 990 nm 和2 400～2 500 nm 的波段删掉，剩余的光谱波段用于进一步研究。在冠层光谱测量之后，就地进行冬小麦采样，采样面积为0.2 m2，随后立即将样品放入塑封袋中，密封并带回实验室。在实验室中，小麦绿叶面积使用Li-3000C 便携式叶面积仪（LI⁃COR，Inc.，林肯，内布拉斯加州，美国）进行测量。

1.3 光谱预处理

导数处理可以消除背景噪声的干扰，分离重叠峰，提高光谱分辨率和灵敏度［16］。在本项研究中，使用光谱反射率的一阶导数（FDR）和光谱反射率的二阶导数（SDR）对原始光谱做预处理。

1.4 特征波长选择方法

1.4.1 随机蛙跳算法

随机蛙跳思想来源于可逆跳的马尔可夫链蒙特卡洛（RJMCMC）框架［17］。由于它不需要严格的数学推导，也不需要像RJMCMC 方法那样指定先验分布，所以实现起来更简单。其算法主要包括3个步骤：（1）随机初始化包含Q 个变量的变量子集V0；（2）基于V0生成一个包含Q*个变量的变量子集V*，以一定概率接受V*，记做V1，令V0= V1，重复这一步骤直到达到预设的迭代次数；（3）计算每个变量的选择概率，作为变量重要性指标。其详细算法见文献［18］。

1.4.2 竞争自适应重加权采样（CARS）

CARS 以迭代方式通过N 次随机采样生成N个变量子集并进而构建N 个PLS 子模型，最后选择具有最低交叉验证均方根误差的波段子集作为特征波段。在每次采样过程中，通过指数递减函数（EDF）和自适应重加权采样（ARS）保留具有较大绝对回归系数的波段。其详细算法见文献［19］。

1.4.3 基于相关系数的选择

相关系数是反映变量之间线性相关程度的统计指标。在光谱分析中，相关系数越高，表明该波段对于待测目标属性越重要。在本项研究中，采用的是Pearson 相关系数。

1.5 建模方法

1.5.1 PLSR

PLSR 是集主成分分析、典型相关分析和多元线性回归分析3 种分析方法的优点于一身的一种技术。它是一种功能强大的建模工具，可以将大量光谱变量减少为几个不相关的潜变量［20］。通过比较采用不同数目的潜变量构建的预测模型的均方根误差（RMSE）的大小，可以确定用于回归的潜变量的最佳个数。PLSR 方法的详细说明见文献［20～22］。

1.5.2 LS−SVR

支持向量机（SVM）是基于统计学习理论和结构风险最小化理论的一种机器学习方法。而最小二乘支持向量机（LS-SVM）是对标准SVM 的改进版本，可以解决线性KKT（Karush-Kuhn-Tuck⁃er）系统［23］。当LS-SVM 用于回归预测，称之为最小二乘支持向量回归（LS-SVR）。其详细的理论介绍参见文献［24］。

1.6 模型评估

本文根据校正集和验证集的均方根误差（RMSE）以及校正集和验证集的决定系数（R2）评估回归模型的性能。根据校正集的交叉验证均方根误差（RMSECV）和交叉验证决定系数（R2CV）进行特征波长的选择。通常，一个好的模型应具有较高的R2和较低的RMSE 值。

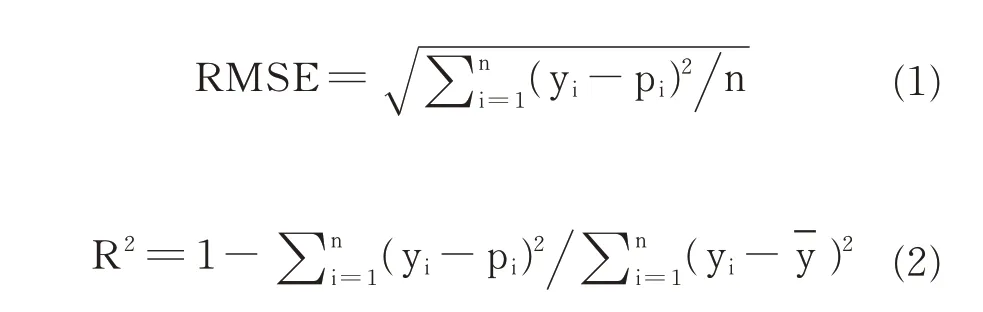
其中，yi，pi分别代表量测值和预测值；代表量测值的平均值；n 是校正集或验证集样品总数。

由于冬小麦采样点的地理位置，天气或小麦作物本身的原因，某些采样点无法正常进行采样工作，最终收集了81 个样本，其中4 个样本因光谱异常而被剔除，剩余的77 个样本用于研究。根据LAI 的大小对样本进行排序，将每连续四个样本中的最后一个作为验证集样本，其余样本作为校正集样本。因此，校正集有58 个样本，验证集有19个样本。

1.7 软件

所有程序均在Matlab 2015a（MathWorks，USA）中实现。

2 结果与分析

表1 为冬小麦LAI 的统计值分析，从表中可以看出，LAI 值的变化范围在1.32 ～9.03，且其平均值为4.26。由于旱地小麦没有灌溉，LAI 相对较低，其变化范围为1.32 ～8.06 之间，平均值为3.63。另外，水地小麦的LAI 相对较高，平均为4.63。图1 是冬小麦LAI 随生育期的动态变化。从图中可以看到，旱地和水地冬小麦的LAI 随时间变化趋势比较相似。在返青期，田间冬小麦的覆盖率很低，冬小麦的LAI 也很低。随着冬小麦的生长发育，其LAI 持续增加。进入孕穗期，冬小麦的LAI 处于峰值。而后进入开花和灌浆期，由于冬小麦的叶片为麦穗提供养分，下层叶子开始衰老并脱落，导致田间冬小麦覆盖率的降低，随之其LAI 也下降。

表1 冬小麦LAI 的统计值分析Table 1 Descriptive statistics of the winter wheat LAI values

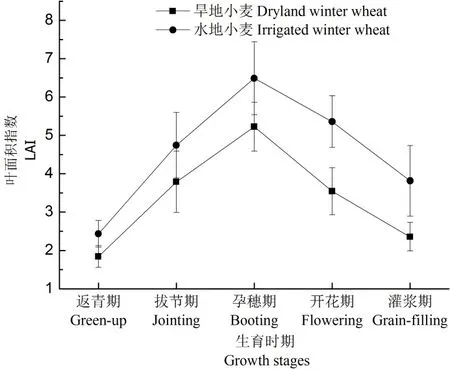
图1 冬小麦LAI 随生育期的动态变化Fig.1 Dynamic change of LAI with respect to growth stages of winter wheat

2.1 LAI 与光谱反射率之间的关系

图2 为LAI 与原始光谱、一阶导数光谱、二阶导数光谱的Pearson 相关系数。对于原始光谱而言，其与L A I 的相关系数在可见光区域（350～740 nm）和长波近红外区域（1 320～1 350nm，1 480～1 780nm 和1 990～2 400 nm）呈负相关，而在近红外区域（740～1 320 nm）呈正相关，相关性比较强的波段位于500～720nm、1 480～1 510nm 和1 996～2 025 nm 区域。其中500～720nm区域主要是由叶片的各种色素引起的，而1 480～1 510nm 和1 996～2 025 nm 位于水吸收带附近。从图上可以看到其相关系数的绝对值不大于0.6，且其相关系数的变化曲线比较光滑。相比之下，一阶导数处理后的光谱与LAI 之间的相关系数在正负值之间来回波动（图2b）。但其相关系数得到了增强，即有更多的波段得到了强化，在754 nm 处其相关系数高达0.648。二阶导数与LAI 的相关系数仅在720～780 nm 范围内显示强相关性，在725 nm 处其相关系数高达0.662（图2c）。值得注意的是具有较高相关系数的波段，在三种不同的光谱预处理中分布在不同的位置。这可能是因为在田间进行光谱测量时，由于外部因素（例如背景土壤亮度，大气影响，叶片角度分布和叶片光学特性等）的影响造成测量的冠层光谱中引入了更多的噪声，从而掩盖了与LAI 相关的光谱信息［25］。另外，对原始光谱进行导数预处理，可以抑制背景噪声的影响，从而使在原始光谱中不明显的那些光谱特征被突显出来［26～28］，这一点在本文中得到进一步证实。此外，Demetriades-Shah 等人［29］提出对冠层光谱使用二阶导数预处理可以消除土壤背景的影响，而一阶导数光谱却不能。

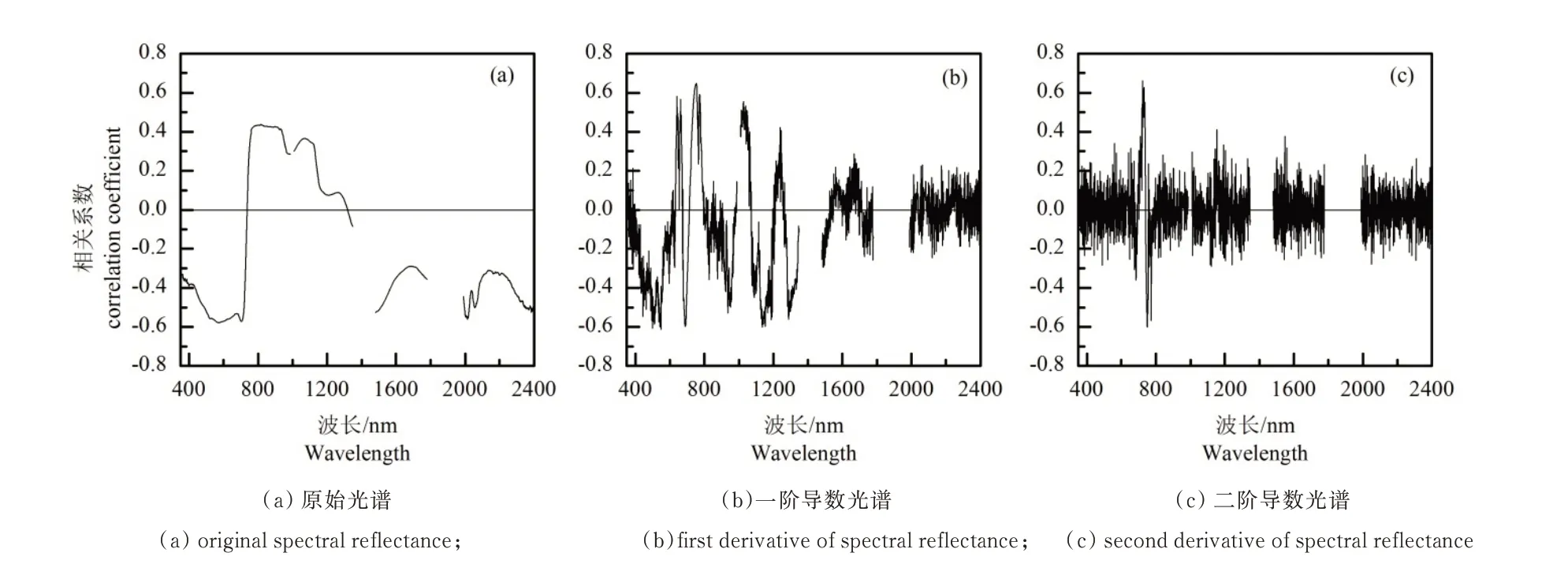
图2 LAI 与不同类型光谱的相关系数Fig.2 The correlation coefficients between LAI and three different spectral expressions

2.2 随机蛙跳变量选择结果

由于随机蛙跳算法是基于蒙特卡洛采样，因此每次运行的结果略有不同。为了减少随机因素的影响，将其重复执行100 次并取平均值作为最终的变量选择概率。图3 为原始光谱、一阶和二阶导数光谱所对应的每个波长的选择概率。从图上可以看出，原始光谱中每个波段的选择概率均低于0.13（图3a），一阶导数光谱中许多波段的选择概率有所提高，最大的选择概率高于0.4（图3b），二阶导数光谱中的许多波段被抑制，敏感波段清晰可见（图3c）。总体而言，绝大多数波段的选择概率都比较低，只有一小部分波段表现出较高的选择概率，而且具有较高选择概率的波段在三种不同光谱中的分布存在着显著差异。这表明与LAI有关的重要波段并不多，在对冬小麦LAI 建模时，对冠层光谱进行特征选择是非常有必要的，而且与LAI 相关的敏感波段不仅存在于红边区域，而且存在于长波近红外区域。与光谱的其他部分相比，红边区域（670～760 nm）被认为包含更多有关LAI 的 光 谱 信 息［30，31］。相 比 原 始 光 谱 和 一 阶 导 数光谱，二阶导数光谱中具有较高选择概率的波段正好位于红边区域内，比如在732 nm 处，其波段的选择概率为0.688，在725 nm 处，其波段的选择概率 为0.572。这一结果与Wang 等［32］（723 nm）和Thenkabail 等［33］（735 nm）的结果非常接近。对于一阶导数光谱而言，具有较高选择概率的前20 个波段中的一半位于800～1300 nm 之间，这些波段主要与叶片内叶肉细胞排列以及冠层结构有关，尤其是垂直叶层数，该区域波段已被证明对LAI估算有效［26］。与图2 比较，可以发现只有在二阶导数光谱中，具有较高相关系数的波段区域与具有较高选择概率的波段区域大致保持一致。这也可能暗示二阶导数预处理可以增强与LAI 有关的重要光谱信号，削弱与其无关的信号或干扰信号［29］。

图3 不同形式光谱下的波段选择概率Fig.3 The selection probabilities of each wavelength of different spectral expressions using random frog method.

2.3 特征波长选择

随机蛙跳算法仅给出了光谱波段的选择概率，但未给出最终选择多少个波段作为特征波段。因此为了剔除冗余的光谱波段，以减小光谱的共线性并增强模型的稳定性，在这里选择前向变量选择程序对波长进行选择。首先对波段按选择概率从大到小进行排序，然后以迭代累加的方式，使用排名靠前的波段构建PLS 模型，并对其进行留一交叉验证评估。在每次迭代结束时，记录模型的RMSECV 和R2CV 以及对应潜在变量的最佳个数。最终具有较少波段数，较小RMSECV 和较大R2CV 的模型即为LAI 预测模型，其所用波段为LAI 预测的特征波段。

图4 为在原始光谱、一阶和二阶导数光谱下，模型RMSECV 和R2CV 随波段选择个数增加的变化。整体来看，采用原始光谱所建模型性能较差，具有最低的R2CV 或最高的RMSECV。相比之下，采用导数处理后光谱所构建的模型，其性能有了很大改善。对于原始光谱而言，当所选波段的个数大于32，模型RMSECV 不再减小，而R2CV不再增大。当选择的波段数为22 时，出现一个小峰值（图4a）。对于一阶和二阶导数光谱而言，当选定的波段数目小于80 时，模型R2CV 随波段数的增加而增加，而RMSECV 随波段数的增加而减小，并且二阶导数的结果要优于一阶导数。但是，当一阶导数所选择的波段数大于27，二阶导数选择的波段数大于22 时，模型R2CV 的增加和RM⁃SECV 的减少变得非常缓慢。当所选波段数超过80 时，模型R2CV 和RMSECV 开始变得不稳定，其值时高时低。此外，当所选波段数超过200 时，R2CV 开始减小，而RMSECV 开始增加。总之，无论使用原始光谱还是一阶或二阶导数，RMSECV都先降低然后增加，相应地R2CV 先增加然后降低。这表明变量的连续添加可能并不总能改善LAI 模型的预测能力，并且某些光谱波段可能并不重要甚至不相关。不太重要或无关的光谱信号可能会对模型预测能力产生负面影响［34］。

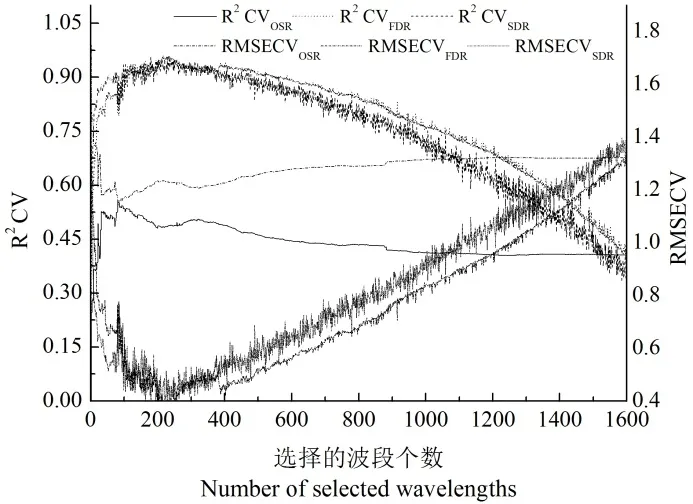
图4 模型RMSECV 和R2CV 随选择波段个数的变化Fig.4 Changes of the RMSECV and R2 CV for the models with different numbers of feature spectra selected from random leapfrog.

2.4 模型建立

为了构建冬小麦LAI 的最佳预测模型，比较了使用3 组光谱（原始光谱，一阶导数光谱和二阶导数光谱），3 种特征波段选择方法（随机蛙跳，基于相关系数的方法和CARS）和2 种建模方法（PLSR 和LS-SVR）所建模型的性能。表2 为不同模型性能的比较，从表2 可以看出，无论采用哪种波长选择方法和建模方法，使用原始光谱建模都不是一个好的选择，其中采用基于相关系数的选择方法和LS-SVR 建模方法所建模型性能相对较好，对校正集而言，其模型R2达到0.623，对验证集而言，其模型R2达到0.322。当对光谱进行导数预处理后，模型性能有了很大的提高，其模型R2增加约20%～30%。这表明建模前对光谱进行预处理是非常有必要的，它能消除背景噪声的干扰，提高光谱分辨率和灵敏度。从所使用的特征波段选择方法角度来看，采用随机蛙跳所建模型的确比基于相关系数和CARS 方法所建模型具有更好的预测能力。相比之下，随机蛙跳算法更适合于冬小麦LAI 预测模型的建立。从建模方法的选择角度来看LS-SVR 的结果要好于PLSR。因此，在本实验中，采用二阶导数预处理结合随机蛙跳和LSSVR 所建模型预测性能最佳，其模型预测R2为0.902，模型预测RMSE 为0.601，并且所选特征波段分别位于438、537、548、559、674、725、728、729、731、732、733、736、751、773、786、825、1 115、1 141、1 142、1 194、1 502、1 546、1 549、1 595、2 002、2 004、2 078、2 050、2 103、2 118 nm。其中，9 个波段位于红边区域（670～760 nm）。

表2 不同预测模型性能对比Table 2 Performance comparison of different prediction models in predicting LAI

尽管在不同学者的研究中，选择的最佳波段组合有所不同，但红边区域波段，短波近红外波段的重要性已得到广泛证明［10～12，26，32，35～37］。将本研究中选择的30 个波段与先前研究中选择的波段进行比较，发现处在红边区域和短波近红外区域的波段与先前报道的一致。但在本研究中，还选择了长波近红外区域的波段作为估算LAI 的重要波段。该区域的波段与冬小麦LAI 之间的关系还有待于下一步的探讨。在利用遥感数据监测农作物LAI 的研究中，已有学者证明，利用SVR 构建的模型性能优于PLSR 模型性能［35，38，39］。本项研究的结果与其结果一致，表明在利用高光谱数据估算冬小麦LAI 时，LS-SVR 是一种非常有力的建模工具。图5 显示了冬小麦LAI 预测值与实测值的对比。

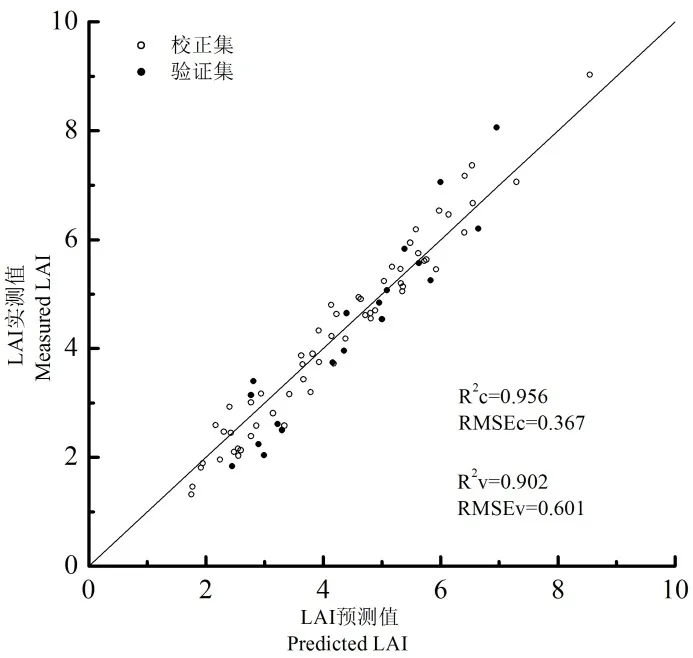
图5 冬小麦LAI 预测值和实测值的对比Fig.5 Scatter plots of predicted LAI against mea⁃sured LAI

3 结论

为了获得一个稳定、高精度、易于实现的冬小麦LAI 估计模型，对原始光谱、一阶和二阶导数光谱，不同的波段选择方法和两种回归模型进行了讨论。在本研究中，二阶导数预处理，随机蛙跳波段选择算法和LS-SVR 的组合被证明可以更好地预测冬小麦LAI。与原始光谱和一阶导数光谱相比，二阶导数光谱变换能更好地消除光谱中的背景噪声。对二阶导数光谱而言，具有较高相关系数的波段和具有较大选择概率的波段位于相同的红边区域（图2c 和图3c）。同时随机蛙跳是一种有效的特征选择方法，它可以从整个光谱中提取少量的重要信息波段，从而简化模型。与PLSR 相比，LS-SVR 可以揭示光谱数据与LAI 之间的非线性关系，提高LAI 的预测精度。