基于SEM、分形理论分析谷子籽粒内部裂纹产生与扩展机理

孙静鑫，郭玉明，崔清亮，许宝卉

（1.运城学院 机电工程系，山西 运城044000；2.山西农业大学 工学院，山西 太谷030801）

谷子籽粒在收获、贮藏及加工过程中由于内力或外力会产生裂纹，籽粒内部裂纹严重影响其贮藏期、降低发芽率［1，2］，内部裂纹的形成主要由热湿内应力和机械作用引起［3～5］。国内外学者对稻谷、玉米等籽粒内部裂纹的检测和形成机理进行了研究分析，Perez 等［6］利用三维有限元分析方法，探究了稻谷籽粒在浸泡过程中因水分梯度引起的拉伸和压缩应力是裂纹形成主要因素；Francis 等［7］提出利用图像扫描技术可以对大米应力裂纹进行评估和量化；Wei 等［8］建立了一种基于多组分非均质性的玉米籽粒水分—热传递和应力模型，利用该模型可预测玉米在干燥时应力裂纹的产生；Ghasemi 等［9］基于应力裂纹指数、回火指数研究了不同品种稻谷多级间歇干燥工艺，确定了应力裂纹最少时的干燥工艺；张新伟［10］研究了玉米籽粒产生裂纹的8 种分形扩展模型，并对模型进行了动力学分析；闫彬应用了机器视觉技术对玉米籽粒内部的机械损伤裂纹进行了检测，裂纹检测平均准 确 率 达90% 以 上［11］；陈 树 人、徐 李 等［12，13］利 用Micro-CT 扫描技术、数字图像处理方法，得到了定量表征谷物内部损伤新模型和不同加载方式下的裂纹扩展规律；崔帆［14］研究了不同含水率和不同压缩方式下糙米应力裂纹的生成和扩展时分形模型；李耀明、侯俊铭等［15，16］基于断裂力学中能量平衡原理得出：水稻籽粒与脱粒元件碰撞时，籽粒内部损伤时断裂面的自由表面能；吴中华等［17］针对稻谷应力裂纹无损检测难的问题，提出可以利用声发射法研究稻谷在干燥过程中产生的应力裂纹；严平宇［18］研究了水稻籽粒在干燥过程中的热质传递模型，得出控制干燥初期的温度，将会减少种子的裂纹；魏硕［19］利用Pro/E 图像处理技术、米塞斯屈服准则揭示了热风干燥过程中玉米籽粒的应力裂纹形成机理；黄小丽［5］基于弹性力学建立了引起稻米过热蒸汽干燥过程中裂纹产生的湿应力方程；张泽璞［20］研究了裸燕麦籽粒沿不同方位压缩时裂纹生成规律。以上研究并未结合扫描电镜等微观技术手段来分析，并且对谷子籽粒内部裂纹产生与扩展机理未见报道，本文采用扫描电子显微镜对裂纹拍照后，结合相关理论对静载压缩试验时裂纹的产生、碰撞时内部机械裂纹产生与扩展的微观机理等进行研究。

1 材料和方法

1.1 试验材料

谷子样本选自山西农业大学试验田，品种为晋谷21，试验时籽粒的含水率为11.1%。

1.2 试验仪器与设备

物性分析仪TA. XT plus（英国Stable Micro System 生 产，测 试 速 度 范 围0.01～40 mm·s-1）；108auto 全自动喷金仪（英国CRESSINGTON）；日立SU5000 扫描电子显微镜（日本日立公司生产）。

1.3 试验方法

挑选完好无损的籽粒在物性分析仪上进行压缩试验，试验时，测前速度为0.5 mm·s-1，压缩速度为0.01 mm·s-1，测后速度为1.0 mm·s-1，触发力为0.049 N，压缩至屈服点时停止，然后利用扫描电子显微镜观察该籽粒剖面及表面微观结构时，将样品按顺序用导电胶粘到样品台上，使用108auto全自动喷金仪对样品喷金镀膜，将样品台放入SU5000 扫描电子显微镜中，抽真空后选择合适的放大倍数进行观察，并拍照保存。

2 籽粒内部裂纹产生机理

根据Griffith 能量平衡理论，可以得到：

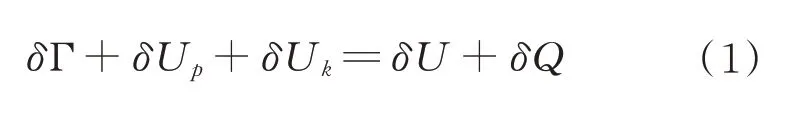
式中，δΓ 为产生新的表面所需要的能量，J；δUp 为弹性变形能（可逆），J；δUk 为动能，J；δU 为输入能量，J；δQ为外界提供给籽粒的热量，J，假设籽粒产生裂纹的过程是绝热过程，δQ=0［21］。则（1）式简化为：

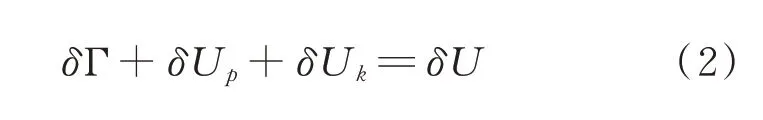
当裂纹沿某一方位δX 产生能量变化时，则（2）式可表达为：

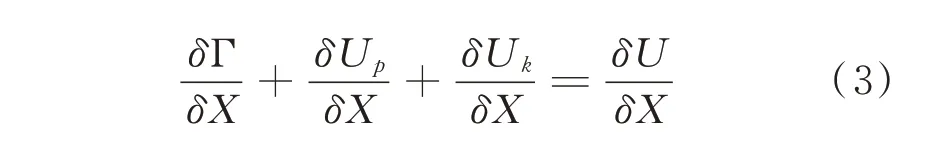
当裂纹沿某一面积δA 产生能量变化时，则（2）式可表达为：

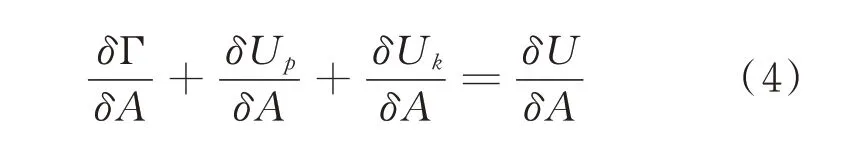
（4）式是符合能量守恒定律的，无论在何种加载方式下都成立。

设籽粒在压缩时产生的裂纹断裂面积为S，在整个裂纹面上对（4）式两端积分得：

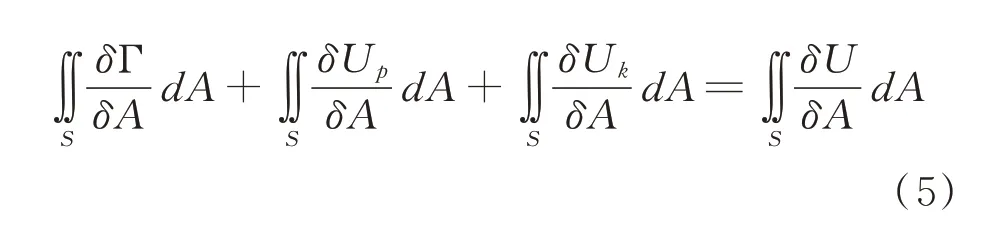
图1 谷子压缩力-位移曲线Fig.1 Compressive force-distance curve of the millet grain

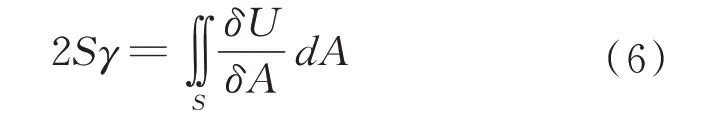
式中，γ 为单位面积的表面自由能，从（6）式可看出，籽粒形成新的表面积的大小与输入能量的大小有关。

谷子籽粒中有微裂纹和空隙，受力后，这些微裂纹和和空隙扩展、延伸形成宏观裂纹。谷子籽粒中微裂纹和空隙的形成过程包含淀粉颗粒之间原子键的断裂，不论局部凝聚力减小到何值，能使淀粉颗粒之间的原子键断裂的应力仍远大于外界作用应力。所以，在谷子籽粒内部的微裂纹形成时存在一个局部增大的应力［3］。Zener 提出，位错塞积处的裂纹形成核［22］，所以在位错塞积前端，局部应力集中，超过籽粒的强度极限就可能形成微裂纹。应用Cottrell 位错反应理论分析谷子籽粒内部微裂纹的产生机理（图2）。

由于位错反应是降低能量的，所以新形成的位错a［001］是不易滑动的，随着位错的不断反应，新形成的位错合并，形成裂纹胚芽。当局部应力σf满足（8）式时，籽粒内部形成微裂纹，即：

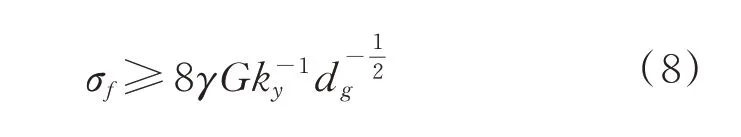
图2 Cottrell 位错塞积模型Fig.2 Model of Cottrell piling up of dislocation

式中，σf为内部局部应力，γ 为单位面积的表面自由能，G 为剪切模量，ky为屈服常数；dg为谷子籽粒淀粉颗粒直径。

3 微观裂纹扩展的fractal 模型

谷子内部的淀粉颗粒为多角体和椭球体［23，24］（图3）：蛋白质主要以蛋白体形式存在于淀粉颗粒的空隙间［25］，与崔婷、郭莲东等人的研究结果一致。为了方便计算，将淀粉颗粒简化为球体，将单个淀粉颗粒与其周围的蛋白体看作是一个圆与其外切正六边形组合的单元［14］。通过分析谷子裂纹的扫描电镜图发现，谷子籽粒微观断裂主要有：沿淀粉颗粒断裂，穿淀粉颗粒断裂，二者的耦合形式断裂。基于3 种断裂形式建立了3 种应力裂纹扩展的fractal 模型：沿淀粉颗粒扩展模型、穿淀粉颗粒扩展模型以及二者的耦合扩展模型。

图3 谷子籽粒内部淀粉粒形态扫描电镜图像Fig.3 Scanning electron microscopic image of starch granules inside millet grain

图4 谷子籽粒内部裂纹扫描电镜图像Fig.4 Scanning electron microscopic image of crack inside the millet grain

利用分形几何原理可以定量描述谷子裂纹，分形维数可通过下式计算：

式 中，D 为 分 形 维 数；N 为 生 成 元 数；r 为 相 似比；Li为 微 观 裂 纹 长 度，εi为 尺 码，LOi为 宏 观 直 线长度。

3.1 沿淀粉颗粒扩展模型

沿淀粉颗粒断裂时，裂纹沿边界扩展，其模型如图5a 所示。

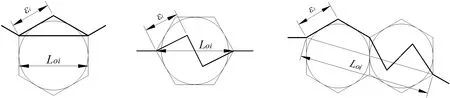
图5 谷子籽粒内部裂纹扩展模型Fig.5 Crack propagation models inside the millet grain

分形维数为：

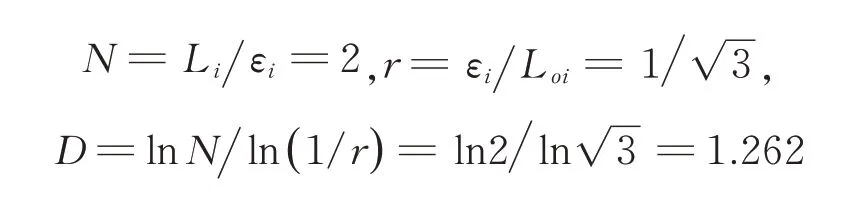
3.2 穿淀粉颗粒扩展模型

通过扫描电镜观察谷子籽粒形成裂纹的显微图像发现，穿淀粉颗粒断裂的情况很少发生，其模型如图5b 所示，主要特征是在一个淀粉颗粒内形成解理“台阶”［26］，其分形维数为：

3.3 沿淀粉颗粒与穿淀粉颗粒耦合扩展模型

观察裂纹的扫描电镜显微图像发现，形成穿淀粉颗粒断裂的单元周围有大量的沿淀粉颗粒断裂单元，因此其模型如图5c 所示，分形维数为：

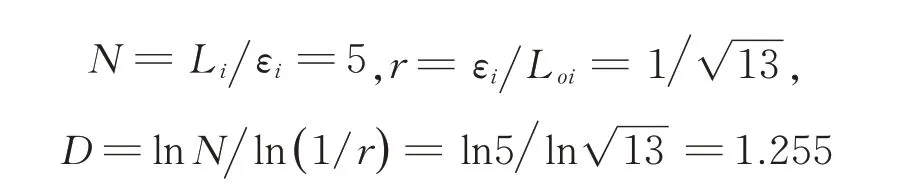
3.4 微观裂纹的分叉模型

分叉现象在谷子内部裂纹形成过程中普遍存在，无论是何种形态的裂纹，在扫描电镜和显微镜适当的放大倍数下，都能观察到微观裂纹的分叉现象（图6a、图6b）。

分叉很大程度上增大裂纹的不规则性，且裂纹的分叉会增大材料的断裂韧性值［14］。微观裂纹分叉系统的生成过程如图6c 所示，假设谷子籽粒内部第（i+1）次的微观裂纹分叉是在前一次，即第i 次裂纹分叉群基础上连续生成的子群，于是形成了一个自相似的分叉系统。以统计角度看，可以近似认为它们具有统计上的自相似性，因此，可以用分形几何理论来模拟这种不规则现象，由此建立的谷子籽粒内部微裂纹分叉扩展模型（图6d）。由几何关系可得分形维数为：

图6 谷子籽粒内部裂纹分叉图像及扩展模型Fig.6 Internal crack bifurcation image and propagation models of the millet grain

式中ψ 为分叉模型中的分叉角，（°）。由上式可看出，分形维数与分叉角呈正相关，分形维数与分叉角的对应关系（表1）。

表1 分形维数与分叉角的对应关系Table1 The corresponding relationship between fractal dimension and bifurcation angles

4 微观裂纹扩展的动力学分析

4.1 微观裂纹的临界扩展力

裂纹生成扩展路径总是曲折的，微观裂纹大多按照“Z”型扩展，并且每一次扩展的方向不同，裂纹的长度、宽窄也不同，小的“Z”型裂纹嵌套在大的“Z”型裂纹上，不同层次的嵌套结构具有自相似性，因此在一定程度上符合分形的自相似性，认为其具有分形结构［14］。

由（9）式可推导出：

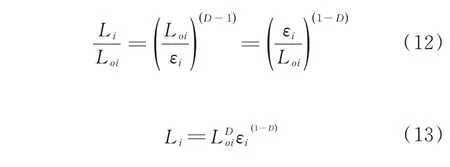
从（13）式可看出，微观裂纹长度Li随着尺码εi的减小而增大，当εi→0 时，Li→∞。但谷子籽粒内部微观裂纹的扩展过程是自然分形过程，尺码εi的大小是有限的，存在一个最大值和最小值，即εmin≤εi≤εmax，在此范围内，微观裂纹的扩展具有自相似的特点，尺码的最小值εmin是断裂表面的最小颗粒尺寸，取决于谷子籽粒的微观结构。由图5 可见，微观裂纹的不规则性主要是由于淀粉颗粒之间的蛋白质间质断裂导致的，因此可以近似地将淀粉颗粒的直径当作最小尺码εmin，即εi=εmin=dg，代入（13）式中，得：

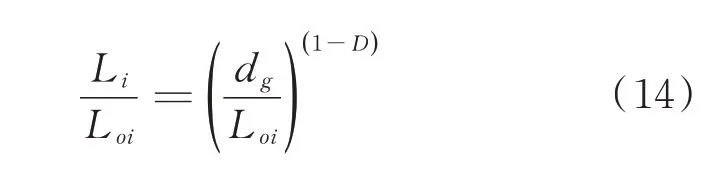
根据Griffth 提出的脆性断裂中，裂纹的临界扩展力［21］计算公式为：

式中γ 为单位面积的表面自由能，但从放大的显微图像观察，裂纹是沿“Z”型弯折扩展的，裂纹微观断裂面积S1大于裂纹宏观断裂面积S2，因此对于S1、S2，有：

式中，L（ε）为微观裂纹的实际长度；L0（ε）为宏观裂纹的实际长度。根据（15）和（16）式可将裂纹的临界扩展力为：

假设L0（ε）为1mm，则：

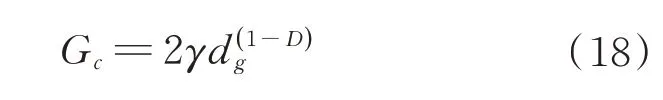
经测量，谷子籽粒内部淀粉颗粒的平均直径为（8×10-3mm），根据本文第3 节计算出不同裂纹扩展模型的分形维数，通过（18）式可计算出裂纹的临界扩展力（表2）。

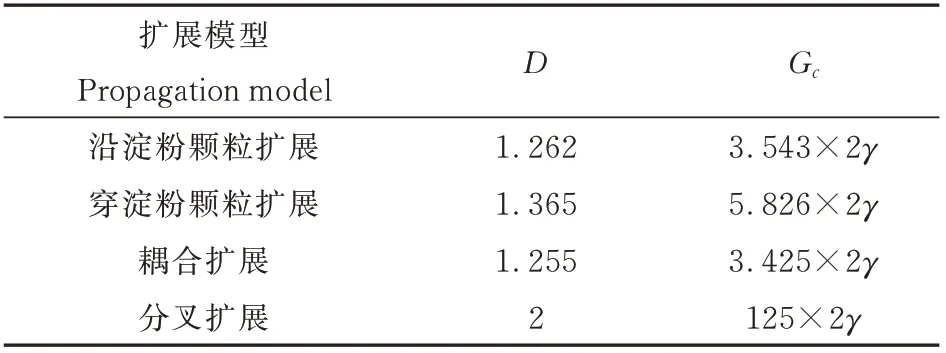
表2 不同裂纹扩展模型的临界扩展力Table 2 Critical propagation force of different crack propa⁃gation models

由表2 可见：同一γ 值，不同裂纹扩展模型的临界扩展力不同，沿淀粉颗粒与穿淀粉颗粒耦合扩展的临界扩展力最小，为6.85γ，分叉扩展的临界扩展力最大，为250γ。所以，沿淀粉颗粒与穿淀粉颗粒耦合扩展的微观裂纹最容易发生，穿淀粉颗粒和分叉扩展的微观裂纹较难发生。

4.2 微观裂纹的的扩展速率

假设谷子籽粒内部有实际长度为L（ε）的微观裂纹，谷子籽粒内部处于能量平衡状态（ΔL（ε）=0），则有：

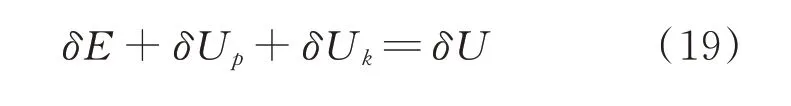
式中，δE 为撞击损伤消耗的能量，J；δUp为弹性变形能（可逆），J；δUk为动能，J；δU 为输入能量，J。

当谷子籽粒内部裂纹开始扩展时，新的能量平衡为：

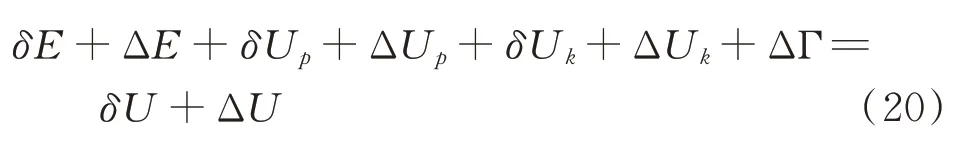
式中，ΔE 为谷子籽粒消耗能量增量，J；ΔUp为弹性变形能增量，J；ΔUk为动能增量，J；ΔΓ 为产生新的表面所需要的能量，J；ΔU 为输入能量增量，J。

新平衡式减去旧平衡式得：

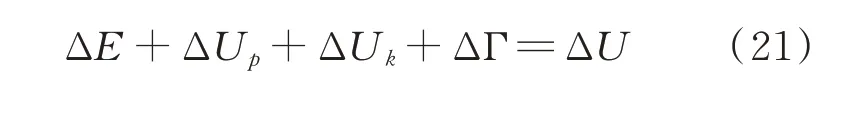
对上式求导得：

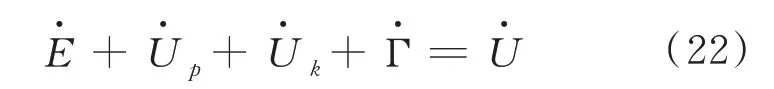
所以，由上式可推导出谷子籽粒内部微观裂纹扩展速率为［3］：

式中，h 为籽粒的高；L（ε）为微观裂纹的实际长度；γ 为单位面积的表面自由能。

上式表明，谷子籽粒受到的外载荷作用将会增大宏观裂纹扩展速率，而微观裂纹的不规则扩展将会减小宏观裂纹扩展速率。假设L0（ε）为1mm，则有：

代入（23）式得：

由表3 可见，对于同一种扩展模型，谷子籽粒内部淀粉颗粒的直径越大，微观裂纹的扩展速率越快；对于同一直径的谷子淀粉颗粒，耦合扩展的速率最快，分叉扩展的速率最小。

表3 扩展模型和淀粉颗粒直径对谷子籽粒裂纹扩展速率的影响Table 3 Effects of crack expansion rate model and starch particle diameter on crack expansion rate in millet grain

3 讨论与结论

通过分析谷子籽粒内部裂纹产生与扩展机理，得到结论如下：

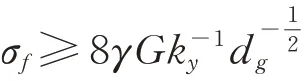
（2）谷子籽粒微观断裂主要有沿淀粉颗粒断裂、穿淀粉颗粒断裂以及二者的耦合形式断裂，3种断裂形式的分形维数分别为：1.262、1.365、1.255，而分叉扩展的分形维数与分叉角呈正相关。对于同一γ 值，不同裂纹扩展模型的临界扩展力差别很大，沿淀粉颗粒与穿淀粉颗粒耦合扩展的Gc<沿淀粉颗粒扩展的Gc<穿淀粉颗粒扩展的Gc<分叉扩展的Gc。所以，耦合扩展的微观裂纹最容易发生，穿淀粉颗粒和分叉扩展的微观裂纹较难发生。

（3）同一种扩展模型，谷子籽粒内部淀粉颗粒的直径越大，微观裂纹的扩展速率越快；同一直径的淀粉颗粒，耦合扩展的速率最快，沿淀粉颗粒扩展的速率次之，分叉扩展的速率最小。

本文研究了静态压缩和单一含水率下谷子籽粒内部裂纹产生与扩展机理，但含水率对谷物籽粒内部裂纹产生、扩展也有一定的影响。不同含水率的糙米断裂面形态不同，微观裂纹的最宽处的宽度随含水率降低而增大［14］；在给仓储环境下稻谷籽粒增湿过程中发现，单裂、双裂及龟裂3 种应力裂纹均有增长，且单裂的增长速率最快、增长幅度也最大，龟裂最小［27］；含水率在21%～25%时，机械脱粒后玉米籽粒单裂、双裂及龟裂裂纹数量最多，而含水率在16%～20% 时，裂纹数量最少［28］。因此压缩速度和籽粒含水率对谷子籽粒内部裂纹产生、扩展的影响还需进一步深入研究。