流花16-2油田钻井返排岩屑堆积参数预测方法*
张伟国 金 颢 李 波 王志远 王 泽 仉 志
(1.中海石油(中国)有限公司深圳分公司 广东深圳 518067; 2.中国石油大学(华东)石油工程学院 山东青岛 266580)
海洋油气开发具有高风险、高技术、高投入等特点[1],因此保证水下管线的正常工作对于海洋油气安全开发具有重要意义。在海洋钻井工程中,返排的钻屑在可行的情况下大多选择排放到海床上以降低钻井运营成本[2],但同时会在钻井现场附近的海床上形成返排岩屑堆积体,可能导致海床不平从而使得生产管汇水下安装[3-7]不能满足工程安全要求。
近年来,国内外相关学者针对石油钻井中水平井、定向井岩屑运移规律做了大量研究[8-10]。刘承婷等[11]通过数值模拟研究了岩屑在不同流动参数下的运移规律,得出了流体黏度对岩屑运移影响最大。闫雪峰[12]通过室内试验和数值模拟相结合的方法,揭示了岩屑颗粒的沉降规律与环空钻井液流速、岩屑颗粒粒径之间的关系。汪海阁、刘希圣[13]进行了大量室内实验,从岩屑颗粒受力分析角度得到了水平井段岩屑运移规律。但海洋钻井返排岩屑在海水中的运移不同于其在井筒内的运移,岩屑在洋流作用下会沿其方向运动,并在垂向上受到重力、浮力、粘滞阻力等作用,同时岩屑性质(粒度分布,密度和球度)和海水性质(密度和黏度)也都会对其运移规律产生影响[14],而对于这种岩屑在非井筒环境中的运移规律研究相对较少。
准确预测不同工况下岩屑堆积体的位置和几何参数是水下生产管线设计的基础,同时也关系到钻井运营成本。本文综合考虑岩屑性质、洋流速度、钻井液排量等对岩屑运移的影响,建立了定量预测海床岩屑堆积体位置和几何参数的岩屑堆积模型,并将预测结果同实际测量结果进行了对比验证,结果表明本文所建的岩屑堆积模型较为合理,可为海上钻井返排岩屑堆积研究提供参考。
1 返排岩屑堆积参数预测模型的建立
在海水中运移的返排岩屑,沿洋流方向,岩屑颗粒受到流动海水的拖曳力而沿其方向运动,沿铅垂方向,在重力、浮力、粘滞阻力作用下做沉降运动,如图1所示。基于岩屑颗粒受力情况,利用牛顿第二定律建立岩屑颗粒运移的动力学模型,综合考虑岩屑上返高度、洋流速度、岩屑性质(粒度分布,密度和球度)和海水性质(密度和黏度)对岩屑运移的影响[2],建立了岩屑运移模型及岩屑堆积模型,并通过迭代法对模型求解。

图1 岩屑颗粒受力示意图Fig.1 Force on cuttings on seabed
1.1 模型假设
本文模型建立过程进行如下假设:
1)岩屑颗粒在洋流方向和重力方向构成二维平面内运动(图2);
2)不考虑湍流对岩屑颗粒运移的影响;
3)不考虑岩屑颗粒之间的相互作用力;
4)岩屑堆积体是由不同粒径岩屑堆积形成的抛物线切片单元组成(图3,岩屑堆积体切片单元i的高是h,底是a,厚度为T)。

图2 岩屑堆积体示意图Fig.2 Schematic diagram of cuttings pile
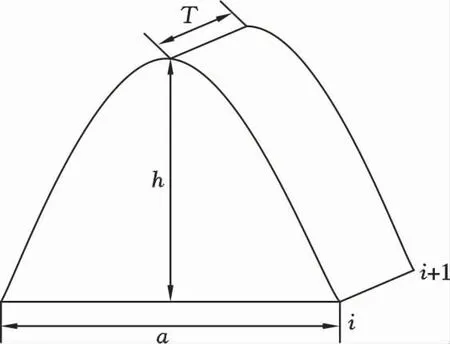
图3 抛物线岩屑堆积单元示意图Fig.3 A sketch of the parabola-slice model
1.2 岩屑运移模型
返排岩屑在钻井液作用下返排出井口具有一定的初速度,在其运移出井口后,在垂直方向受粘滞阻力、重力、浮力等作用下岩屑垂向速度降低为0后到达最大上返高度H(距离井口)。随后岩屑受力如图1所示,垂向上在重力、浮力、粘滞阻力等作用下将会形成垂直向下的加速度,洋流方向受到粘滞阻力形成沿洋流速度方向的加速度,则岩屑的运移过程可简化为颗粒的抛物线运动,即当颗粒处于上升阶段时在x、y方向有[2]:

当颗粒处于下降阶段时在x、y方向有[15]:

式(1)~(4)中:B为浮力,N;D x为水平方向粘滞阻力,N;D y为铅直方向粘滞阻力,N;v x为颗粒在洋流方向的速度分量,m/s;v y为颗粒在重力方向的速度分量,m/s;gc为重力加速度,m/s2;mp为岩屑质量,kg;W为重力,N。
设δ为岩屑初始速度与垂直方向的夹角,则初始条件岩屑颗粒返出井口时v y=v0cosδ=v y0,v x=v0sinδ=v x0,对式(1)、(2)积分得到颗粒处于上升阶段时沿洋流速度方向岩屑运移速度v x,垂直于洋流速度方向运移速度v y:

其中

式(5)~(8)中:vf为洋流速度,m/s;f为粘滞阻力系数[16],无量纲;A为岩屑的横截面积,m2;ρf为岩屑密度,kg/m3;v x0为水平方向初始速度,m/s;v y0为铅直方向初始速度,m/s;Cx、Cy、α、β为积分变量。
对式(1)、(2)积分,得到岩屑上升阶段运移距离x,垂直于洋流速度方向运移距离y:
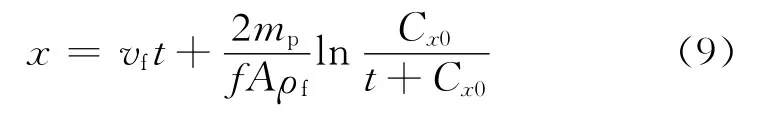
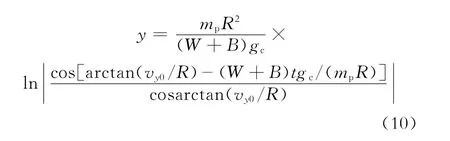
当岩屑颗粒垂直方向粘滞阻力、重力、浮力作用下v y降低为0时意味着运移过程上升阶段的结束,取v y=0可得上升阶段结束后对应的岩屑颗粒沿洋流速度方向速度v x=v x1,此时的时间记为t1,Cx1是关于v x1的函数关系式,以此作为颗粒运移过程下降阶段初始条件,积分式(3)、(4)得颗粒处于下降阶段时沿洋流速度方向岩屑运移速度v x,垂直于洋流速度方向运移速度v y:

岩屑运移距离x,垂直于洋流速度方向运移距离y:
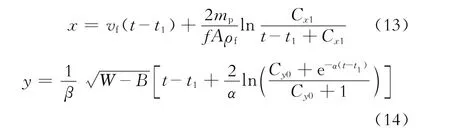
其中
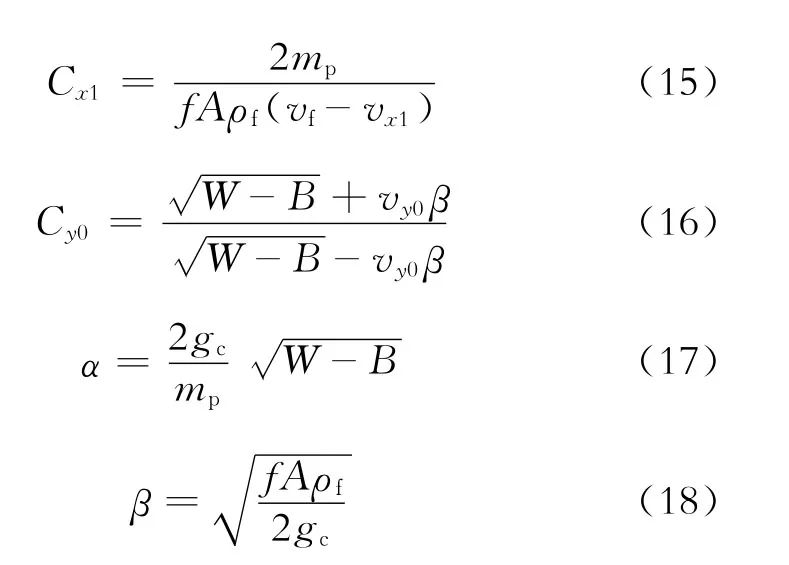
式(11)~(18)中:Cx、Cy、α、β为积分变量。
关于f的求解,根据Bourgoyne等[17]测量了不同粒径、球度颗粒在流场不同雷诺数下的摩擦系数所得的图表,本文将图表拟合为:

其中

式(19)、(20)中:Ψ为岩屑球度,无量纲;Re为雷诺数,无量纲,在x方向表达式为

在y方向表达式为

式(21)、(22)中:μ为海水黏度,mPa·s;dp为岩屑直径,m。
1.3 岩屑堆积模型
由于岩屑的重量和尺寸不同,其水平漂移距离也不同,依据前文假设,在已知返出岩屑总体积的条件下,不同粒径岩屑所形成的抛物线切面堆积单元(图3)可由其所占比例来计算。假设岩屑有N种不同的粒径,则每种粒径岩屑所占比例可表示为

式(23)中:fvi为每种粒径岩屑所占比例,%;dpi为岩屑直径,m;
设岩屑总体积为V,则每种岩屑所占体积为

根据式(9)、(13)可分别得到岩屑颗粒上升阶段和下降阶段的水平运移距离,记x i和x i+1分别是颗粒i和i+1的水平漂移距离,堆积单元i的间距可表示为:

根据图3所示岩屑堆积体单元,则堆积单元宽度和高度表示为:
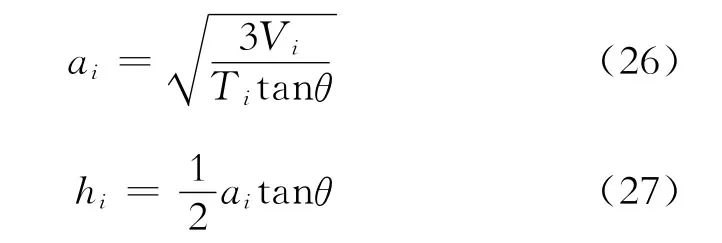
式(26)、(27)中:ai为堆积单元的宽度,m;h i为堆积单元的高度,m;θ为堆积角,(°),取值为32.5°[2]。
1.4 模型求解方法
综合考虑返排岩屑初速度、洋流速度、岩屑性质(粒度分布、密度和球度)和海水性质(密度和黏度)对岩屑运移的影响,建立了岩屑运移模型;考虑不同颗粒岩屑所占体积、运移间距及抛物线切片单元的堆积角建立了岩屑堆积模型。记岩屑为标准球形,通过引入球度概念来定量表征岩屑颗粒形状对运移及堆积过程的影响,提高模型的精确性。
模型计算:岩屑颗粒的运动过程分为上升和下降两个阶段,两个阶段的模型计算过程是一样的。由给定岩屑上返速度v x0、v y0代入式(5)~(10),求得岩屑上返高度y以及上升阶段运移时间t1,将岩屑上返高度y以及上升阶段运移时间t1代入式(14),结合式(17)、(18)求得岩屑运移过程所经历的时间t。其中求解摩擦系数f需要计算雷诺数Re,而Re的计算则需要求解洋流速度方向速度v x,铅垂方向速度v y。又v x、v y是需要求解的中间参数,所以模型的求解必须使用迭代法。对于大尺寸岩屑和高洋流速度时,摩擦系数对颗粒雷诺数和颗粒球度不敏感。在这些条件下,摩擦系数可以认为是常数值。由式(19)求得f,将f、t、t1、Cx1代入式(13),结合式(15)、(19)求得水平方向运移距离x,以颗粒i和颗粒i+1为例,由式(25)确定不同粒径岩屑形成三角形堆积单元所占间距T i,通过给定返排岩屑总体积V,由式(24)求得颗粒i所占体积V i,最后由式(26)、(27)确定岩屑堆积体各几何参数ai、hi,具体流程如图4所示。
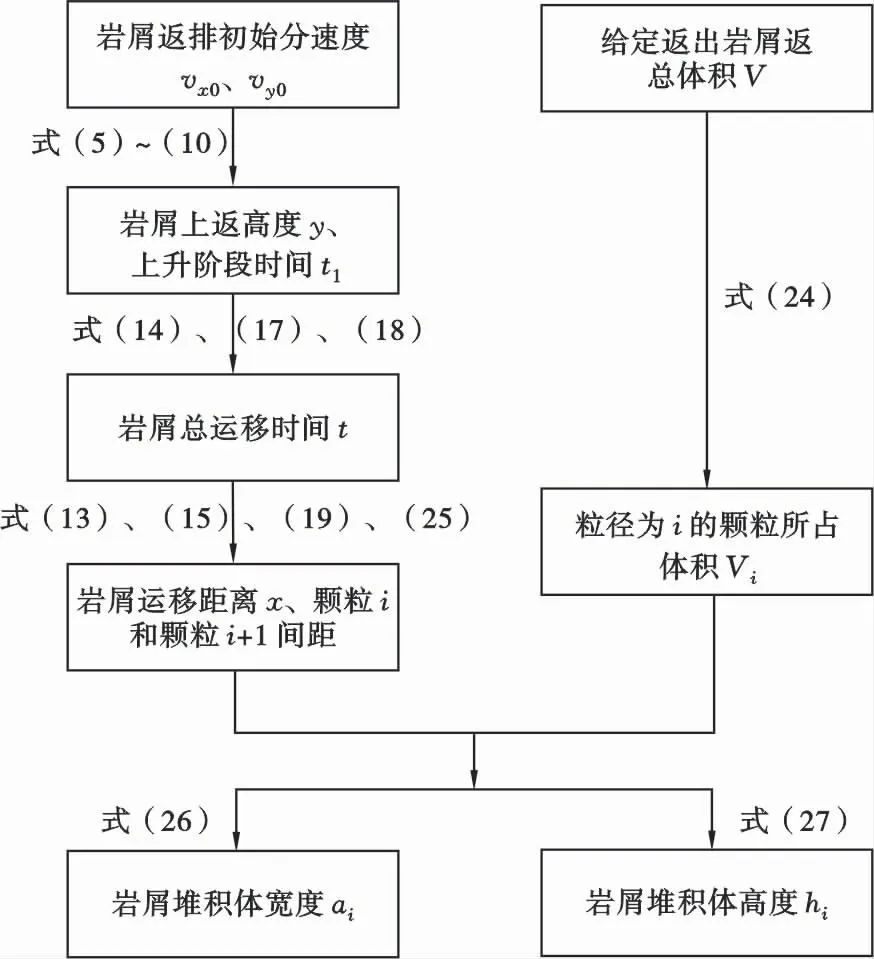
图4 岩屑堆积几何参数预测模型计算流程图Fig.4 Calculation flow chart of prediction model for geometric parameters of cutting piles
2 现场应用分析
以位于我国南海流花16-2油田LH16-2-A1井为例,该井因忽略海床岩屑堆积体的影响导致水下生产管汇安装不满足安全标准,油田基本参数见表1,该井钻进参数见表2。

表1 流花16-2油田基本参数Table1 Basic data of LH16-2 oilfield

表2 LH16-2-A1井钻进参数Table2 Well drilling parameters of Well LH16-2-A1
由于表层钻进时未安装井口与隔水管,岩屑直接排放于海床上,无法通过固控系统分析岩屑粒径分布,该井通过地层钻探取样方法获取堆积体岩屑样本,过滤掉钻井液与海水,在现场用清水对岩屑颗粒中的泥和黏土进行简单冲洗、烘干后获得粒径分布见表3。

表3 岩屑粒径分布及各自所占比例Table3 Cuttings size distribution and proportion
2.1 模型计算结果及误差分析
堆积体几何参数实测值与模型计算值见表4,由表4可知,洋流方向堆积范围相对误差不超过14.66%,相对误差来源于模型假设,洋流运动的涡旋、脉动速度,岩屑颗粒之间的相互作用。堆积体最大宽度、最大高度相对误差不超过14.19%,相对误差来源与堆积角的实验测定无法完全模拟还原海床环境。综上,模型预测结果相对误差在15%以内,证明模型预测结果合理。

表4 LH16-2-A1井堆积体几何参数Table4 Geometric parameters of the accumulation body of Well LH16-2-A1
2.2 岩屑运移规律分析
2.2.1 粒径-球度对岩屑运移距离的影响
岩屑运移距离随粒径-球度的变化关系如图5所示,由图5可以看出:
1)在岩屑球度一定的情况下,运移距离随粒径的增大而减小,分析其原因在于,随粒径的增大,岩屑所受重力的增大幅度大于浮力加粘滞阻力的增大幅度(图6),使得岩屑在垂向加速度增大,运移时间缩短,从而运移距离变短。2)在岩屑粒径一定的情况下,运移距离随球度的增大而减小,分析其原因在于,当考虑球度[14]对沉降的影响时,颗粒直径应用体积当量直径dv表示,此时颗粒截面积A,体积V表示为:


式(28)、(29)中:dv为当量直径,mm。

图5 岩屑运移距离随粒径-球度变化曲线Fig.5 Cuttings migration distance with particle sizesphericity curve

图6 岩屑受力随粒径变化关系(球度0.5,时间0)Fig.6 Curve between cuttings force and particle size(sphericity is 0.5,time is 0)
则上升阶段垂直方向受力表达式为[18]:
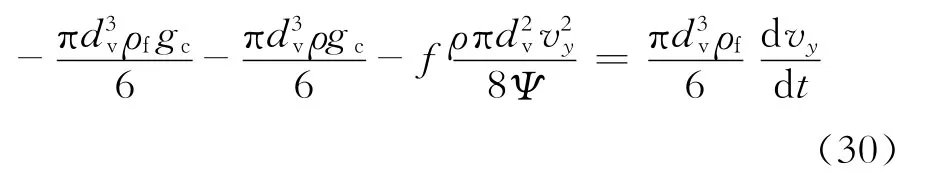
下降阶段垂直方向受力表达式为:

通过式(30)、(31)可以看出,因为0<Ψ≤1,导致当颗粒为非球形时粘滞阻力项大于其为球形颗粒时的粘滞阻力,使得当颗粒为非球形时上升阶段垂向加速度增大,具有减小运移时间的趋势;下降阶段垂向加速度变小,具有增大沉降时间的趋势。图7反映了运移时间随球度的变化关系,可以看出随着球度的减小,下降阶段运移时间的增大幅度大于上升阶段运移时间的减小幅度,运移距离随球度的减小而增大。

图7 岩屑运移时间随球度变化关系(粒径3 mm)Fig.7 Curve between cuttings migration time and sphericity(particle size is 3 mm)
2.2.2 粒径-洋流速度对岩屑运移距离的影响
岩屑运移距离随岩屑粒径-洋流速度变化关系如图8所示,由图8可以看出,岩屑运移距离随洋流速度的增大而增大,其原因在于增大的洋流速度导致水平方向粘滞阻力增大,使得水平方向加速度增大;垂直方向受力没有变化,所以运移时间不变;岩屑颗粒粒径大于1 mm、洋流速度小于0.1 m/s时,岩屑主要堆积在井口附近。

图8 岩屑运移距离随岩屑粒径-洋流速度变化图(球度0.5)Fig.8 Curves of cuttings migration distance with cuttings particle size-ocean current velocity(sphericity is 0.5)
2.2.3 粒径-钻井液排量对岩屑运移距离的影响
岩屑运移距离随岩屑粒径-排量变化关系如图9所示,由图9可以看出,岩屑运移距离随钻井液排量的增大而增大,分析其原因在于一方面一开钻进钻井液排量大于表层钻进,使得岩屑上返高度增大,运移时间变长;另一方面,钻井液排量的增大使得射流冲击力增大,岩屑破碎将更不规则,球度变小。对于流花16-2油田丛式井生产,当排量小于4 200 L/min,岩屑颗粒粒径大于1 mm时,形成岩屑堆积体距井口不足50 m,存在堆积体堵塞临井井口的隐患;当排量大于4 200 L/min,形成岩屑堆积体距井口大于50 m,较为安全。流花16-2油田一开钻进岩屑运移距离大于表层钻进岩屑运移距离(图10),且变化趋势同模型计算具有较高的一致性,证明粒径和钻井液排量两者综合作用共同导致岩屑堆积体现状(图11)。

图9 岩屑运移距离随岩屑粒径-钻井液排量变化图Fig.9 Cuttings migration distance with cuttings particle size-drilling fluid displacement

图10 一开表层岩屑运移距离随粒径变化图Fig.10 Variation of the cuttings migration distance with particle size in surface and opening drilling
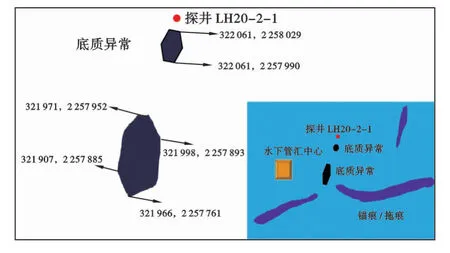
图11 流花16-2油田岩屑堆积体示意图Fig.11 Cuttings pile of LH16-2 oilfield
3 结论与建议
1)综合考虑钻井液性质,岩屑性质等对运移的影响,建立了岩屑堆积几何参数预测模型,该模型由岩屑颗粒运移模型和岩屑堆积模型组成,实例验证结果表明,所建立的岩屑堆积几何参数预测模型具有较高的精确度,可满足现场需要。
2)根据流花16-2油田丛式井LH16-2-A1井生产岩屑运移规律分析结果,当排量小于4 200 L/min,洋流速度小于0.1 m/s时,形成岩屑堆积体距井口不足50 m,存在堆积体堵塞临井井口的隐患,建议增大钻井液排量以增加岩屑运移距离,从而保障邻井井口安全,同时建议生产管汇设计综合考虑钻井返排岩屑堆积对海床起伏影响。

