高含沙水流作用下水垫塘底板上举力特性试验

刘 昉，李晓娜，周世佳

(天津大学水利工程仿真与安全国家重点实验室，天津 300350)

近年来我国高坝建设进入了快速发展的阶段，截至2016年，我国200 m以上已建、在建的大坝达到20座，有的甚至已经超过300 m[1]。这些水利枢纽大多建于狭窄河谷，泄流量大加上水头高，往往泄洪功率极大，如二滩、小湾、构皮滩和溪洛渡等高坝工程，下泄水流速度达到50 m/s左右，泄洪流量超过2×104m3/s[2-4]。为了能安全经济地宣泄洪水，一般通过建二道坝、尾坎或利用下游围堰形成水垫塘来进行消能。水垫塘内水流流态复杂、紊动剧烈，混凝土底板作为水垫塘内的衬砌防护结构，需要抵抗水流产生的冲击荷载，尤其在底板缝隙间止水破坏后，动水压强沿缝隙传至底板下部，从而形成巨大的上举力，当上举力大于底板本身自重与锚固力之和后，板块就会发生浮升失稳，严重威胁大坝安全。因此确定水垫塘底板在高速射流冲击作用下的上举力是保证消能防冲安全的关键所在[5]。

近些年来关于底板上举力的成因机理及其特性的研究已经有了比较丰硕的成果。普遍认为，高坝下游基岩缝隙内脉动压力是底板掘起或翻转出穴的重要条件。基于这一理论，赵耀南等[6]提出了岩块缝隙中压强传播的水流振荡模型；刘沛清等[7]利用瞬变流模型，导出了岩块上可能出现的最大脉动上举力的计算公式；李爱华等[8]对底板缝隙中脉动压强传播的3种模型进行了算例分析，总结了各模型的适用情况。杨敏等[9]基于模型试验研究了水垫塘透水底板的水动力特性，指出适当的透水孔能够有效地减小底板上举力；马斌等[10]通过建立有限元分析模型，研究了键槽设置方式对消力塘底板稳定性的影响，结果表明设置键槽可以有效地减小底板动力响应，增加底板稳定性。上述研究多是针对清水条件下上举力的特性，而水流含沙后对水垫塘底板上举力的影响却很少被研究。

我国河流大多挟带泥沙，北方河流以含沙量高著称，尤其是黄河某些支流的最大含沙量可达1 700 kg/m3。在利用水垫塘消能防冲时，难以保证塘内无泥沙、卵石等杂质，一旦水流携带推移质，必定会对底板产生不同程度的磨损，而水流携带悬移质，势必影响挑跌流水舌在水垫塘底部的脉动程度[11]，因此正确估算含沙水流作用下水垫塘底板的上举力，对高坝下游消能防冲结构的合理设计具有十分重要的工程实际意义。本文通过物理模型试验，分析水流含沙量对上举力的影响。

1 模型试验概况

模型试验装置如图1所示，主要由上游试验水槽、下游蓄水池、管道泥浆泵、电磁流量计和输水管道组成。试验中通过控制泥浆泵的转速来改变射流速度，由流量计测量管道内流量。输水管道为内径0.20 m的铁管，管道末端的喷嘴内径为0.07 m。上游试验水槽长2.0 m，宽和高均1.0 m，在试验水槽底部铺设一层尺寸为20 cm×20 cm×6 cm(长×宽×高)的板块来模拟水垫塘底板，底板布置如图2所示。由于在所有缝隙均贯通的状态下，底板会瞬间失稳，因此在板块之间及板块与水槽底板之间留有一定宽度的缝隙。杨敏等[12]从缝隙流属于层流这一观点出发，通过建立模型与原型缝隙流速度间的比例关系，认为模型与原型的缝隙间距为同量级，故考虑到工程实际情况，本试验缝隙宽度均取2 mm。在与泄流中心线对应的一列板块下布置了9个上举力传感器，分别用来测量图2中1～9号板块的上举力，每个板块通过4个螺栓与其对应的传感器连接组成一个测力系统，传感器使用的是S形拉压力式称重传感器，上举力测量系统如图3所示。信号的采集使用的是INV306U-6260数据采集仪以及配套的DASP软件，采样频率为200 Hz，采样时长为60 s。

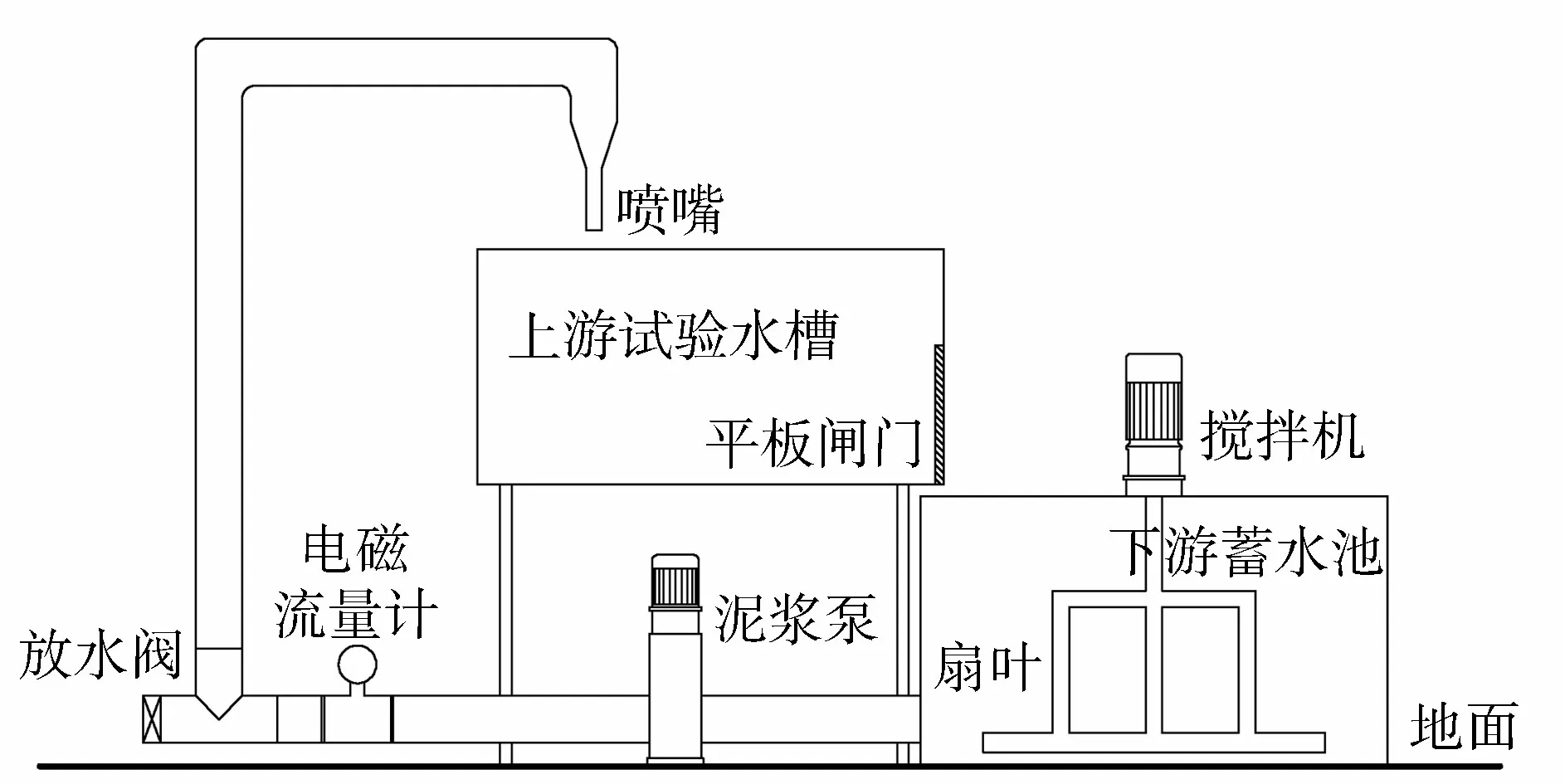
图1 试验装置

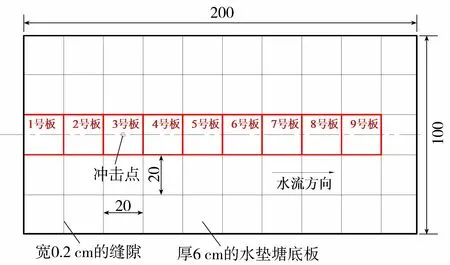
图2 试验底板布置(单位：cm)

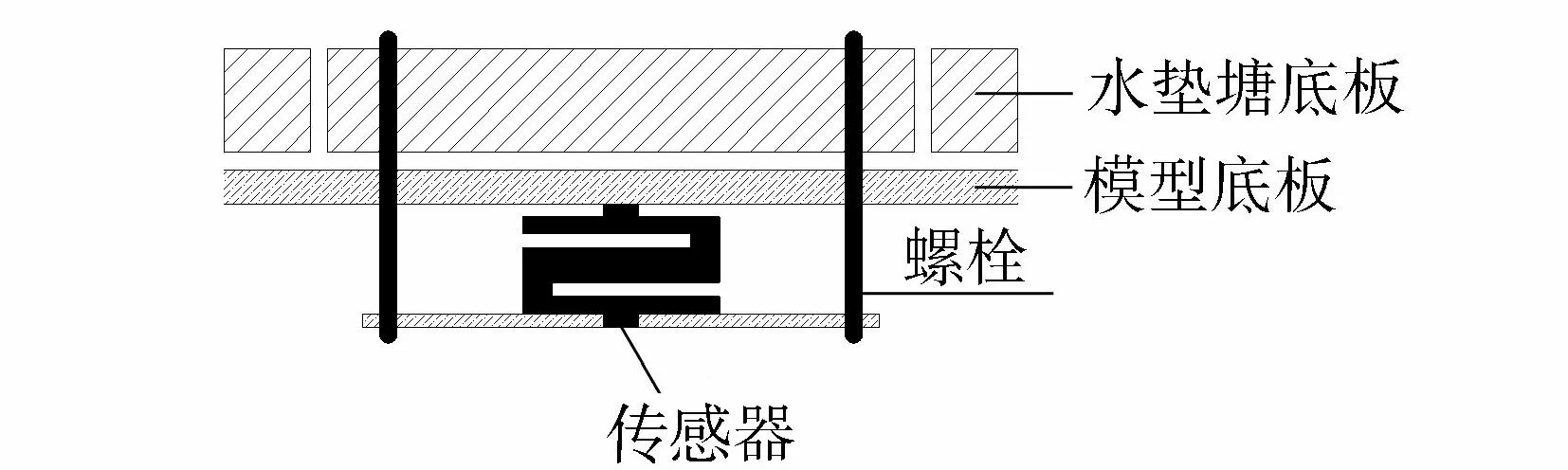
图3 上举力测量装置

试验所用沙的堆积密度为1 207 kg/m3，颗粒级配曲线如图4所示，中值粒径约为0.05 mm。试验分别在0 kg/m3(清水)、52 kg/m3、92 kg/m3、183 kg/m3、244 kg/m3、349 kg/m3共6种含沙量s条件下进行，每种含沙量下设置4种不同的射流速度u，分别为8.44 m/s、10.54 m/s、11.55 m/s、13.50 m/s，共计24个试验工况。水舌从圆管喷嘴流出并垂直入水，试验中保证水垫深度为0.6 m，入水前的水舌长度为0.45 m。

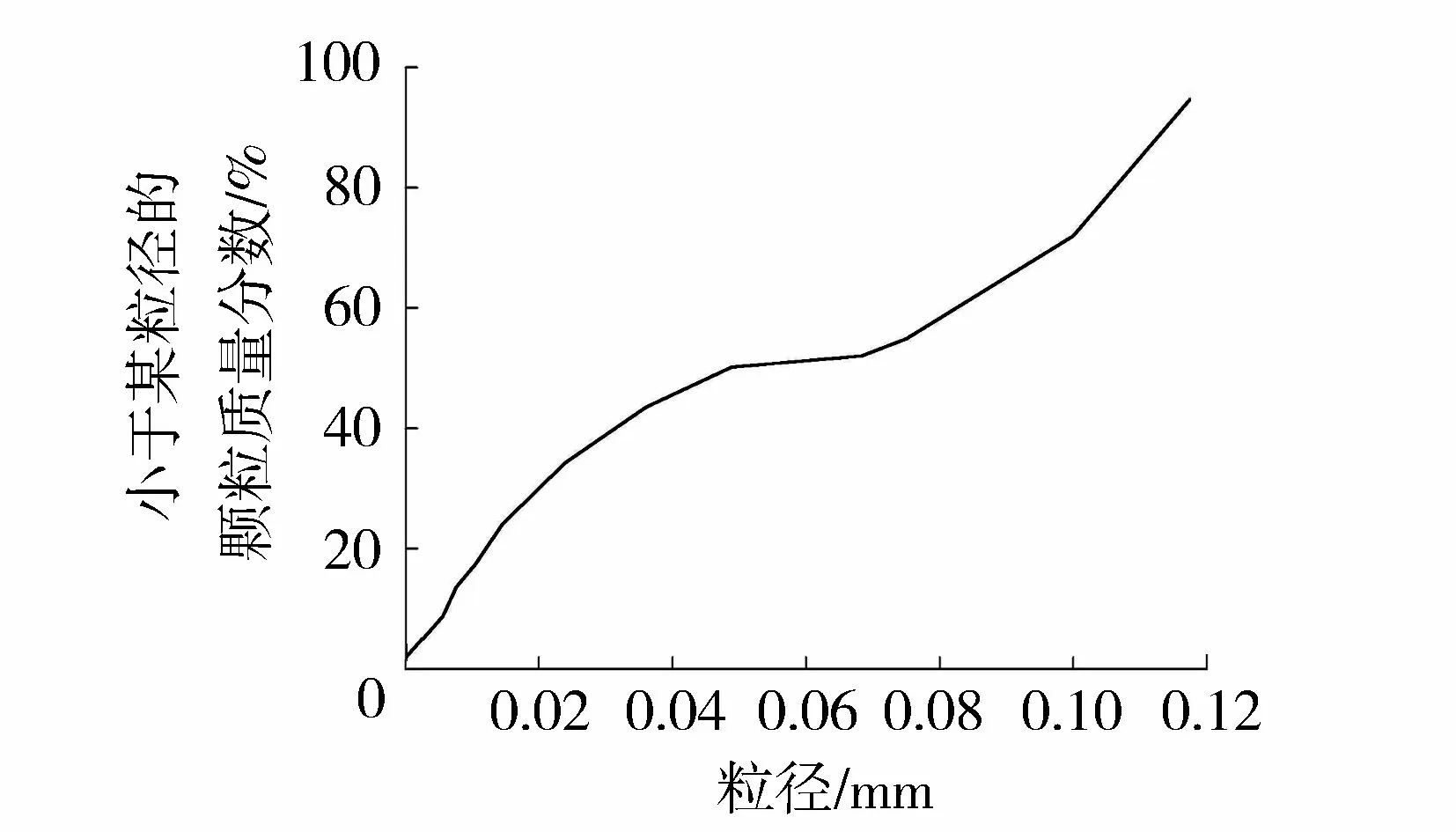
图4 试验用沙颗粒级配曲线

2 试验结果与分析

2.1 上举力沿程分布规律

为了研究底板上举力随底板位置的变化规律，图5给出射流速度为8.44 m/s时，不同含沙量下顺水流方向的板块所受的上举力时均值、标准差及最大值。

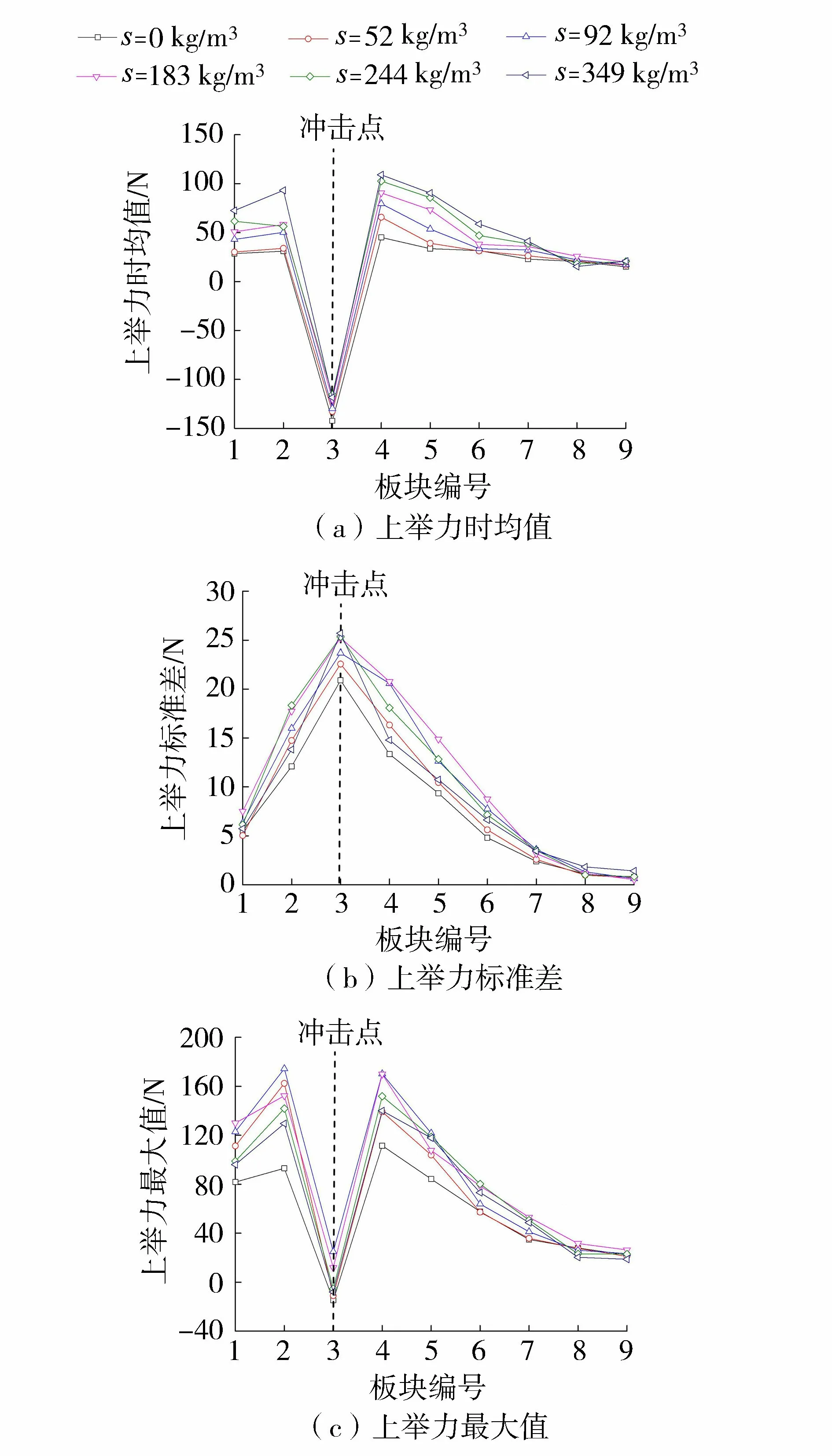
图5 u=8.44 m/s时板块上举力沿程分布

由图5可以看出，在不同浓度的含沙水流下，上举力时均值、标准差、最大值的分布规律均与清水条件下的分布规律相似。由图5(a) (b)可知，射流直接冲击的3号板块所受的上举力时均值为负值，2号与4号板块的上举力时均值迅速增大为正值，随着与冲击点距离的增加，板块的上举力时均值逐渐减小；上举力标准差在3号板块处取得最大值，随后向上下游两侧逐渐下降，并在9号板块处达到零值附近。由图5(c)可得，上举力最大值与上举力时均值的沿程分布趋势基本相同，在3号板块处取得最小值，并在其左右两侧迅速增大，随后沿程逐渐减小，但随着距离的增加，上举力最大值减小的速率比上举力时均值减小的速率快，其原因可能是由于最大上举力是由上举力时均值与上举力脉动值共同决定的，上举力标准差随着距离的增大而减小，使上举力值更加集中，即上举力脉动的程度减弱，从而最大上举力出现的概率也相应减小。

由图5(a) (b)可知，虽然直接作用于3号板块的上举力脉动比较剧烈，但其时均上举力为负值，因此对于时均上举力而言，该板块并不会发生失稳。在除3号板块外的其他区域，动水压力差的方向向上，板块均有可能发生失稳，尤其4号板块处的上举力时均值、标准差、最大值均相对较大，是试验范围内最容易失稳的板块，这与文献[13]得出的结论一致。另外由图5可以看出，含沙量的变化会对上举力幅值有所影响。

2.2 上举力幅值特性

含沙量对上举力的影响可以从时均值与标准差两个方面进行分析。图6给出了射流速度不同时4号板块上举力时均值与含沙量的关系。由图6可知，当流速一定时，在试验含沙量范围内，上举力时均值随含沙量的增大而增大，流速为8.44 m/s时，水流含沙量从0 kg/m3增大到349 kg/m3，上举力时均值增大了64 N，流速为10.54 m/s、11.55 m/s、13.50 m/s时，时均值分别增加了77 N、75 N、60 N，不同流速下上举力时均值随含沙量的变化均基本呈线性函数关系，且斜率大致相同，均在0.17～0.22之间。时均上举力随含沙量的增大而增大的原因可能是：上举力是由底板上下表面的压力波幅值及相位不同引起的，产生4号板块上举力的能量是由射流冲击区的能量以压力波的形式传递的，因此上举力大小随含沙量的变化主要取决于射流冲击区水流能量随含沙量的变化。在相同流速条件下，随着含沙水流浓度增加，水体密度也增大，其所蕴含的动能增加，由射流冲击区的动能转化的4号板块向上的压能也随之增加，从而作用于底板的上举力时均值随含沙量的增大而增大。

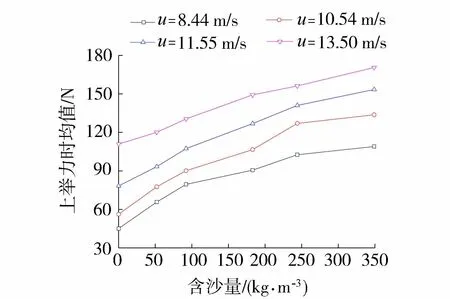
图6 4号板块上举力时均值与含沙量的关系

上举力标准差在一定程度上反映的是作用于底板的上举力的脉动程度。图7为不同流速下，4号板块上举力标准差与含沙量的关系。从图7可以看出，各流速条件下，上举力标准差在含沙量为183 kg/m3时出现峰值，含沙量小于183 kg/m3时，上举力标准差随着含沙量的增大逐渐增大，含沙量超过183 kg/m3后上举力标准差随含沙量的增大逐渐减小，且减小的速率随着流速的增大而变缓，其中，射流流速为8.44 m/s时，上举力标准差的峰值较相同条件下的清水时增加了约7.4 N，流速为10.54 m/s、11.55 m/s、13.50 m/s时，上举力标准差的峰值相比清水时分别增加了8.2 N、6.9 N、4.4 N。

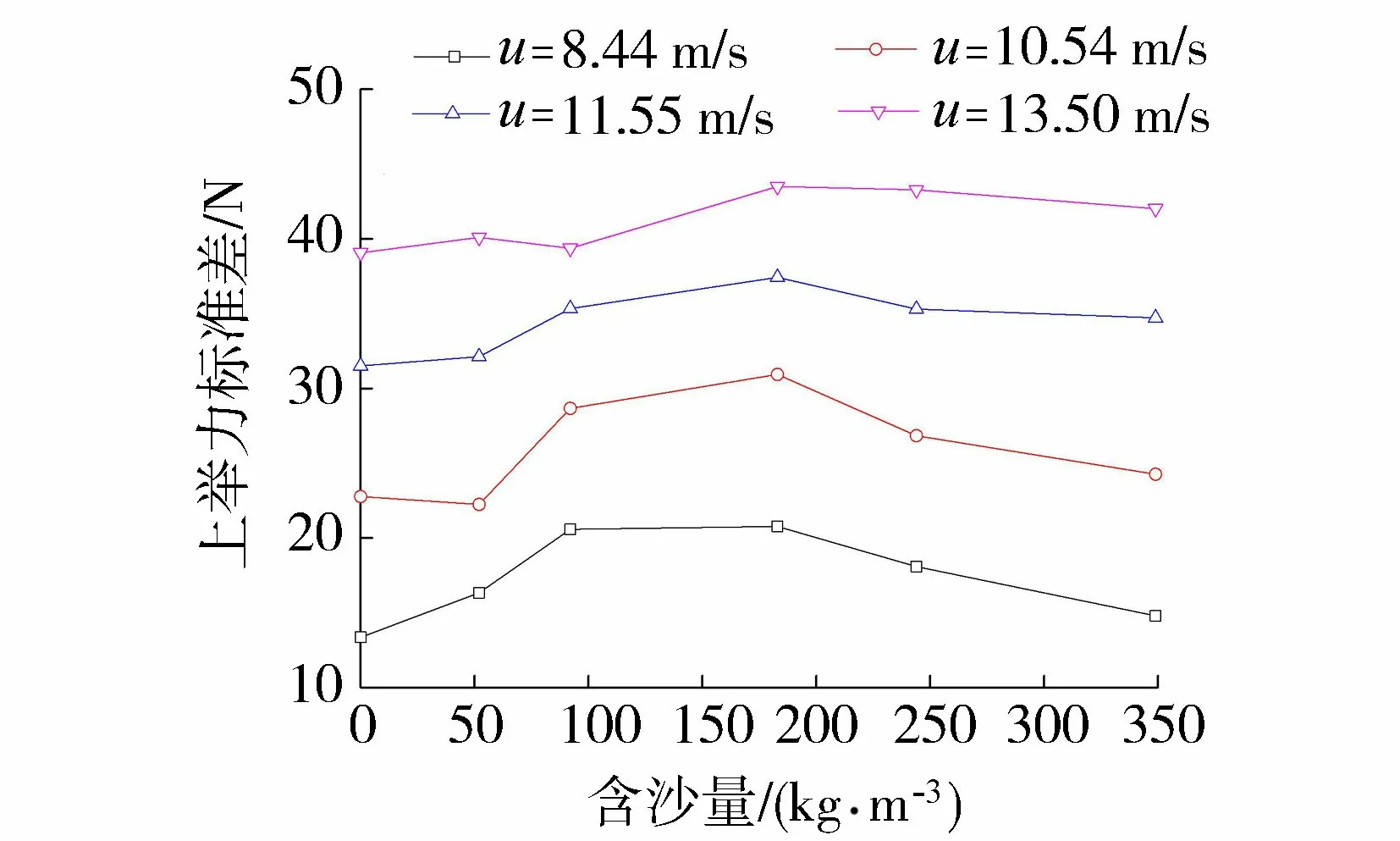
图7 4号板块上举力标准差与含沙量的关系

上举力标准差随含沙量变化出现峰值的原因可能是：在含沙量较低时，由于粗细泥沙颗粒在水中的悬浮指标不同，水流下层的粗颗粒较多，粗颗粒泥沙落在底板缝隙之间，在水流的作用下发生推移质运动，使脉动压力在传递过程中受到阻尼作用，从而脉动能量更多地转化为紊动能，使底板紊动加剧，继续增加含沙量，紊动能的转化率越高，底板脉动程度越大，反映在4号板块所受的上举力结果上，表现为上举力标准差随含沙量的增加而增加，但是当含沙量超过一定值后，水流的黏性作用加强，细颗粒相互黏结形成絮团结构，水流的紊动能被絮团结构消耗，从而抑制了水体的紊动，降低了板块的波动性，导致上举力标准差逐渐减小。由文献[14]可知，在脉动压力随含沙量变化过程中，存在一个含沙量临界值，当含沙量小于或大于该临界值时，水流脉动压强均减小。考虑到上举力是由脉动压力传到底板底部而产生的[15]，因此本试验中上举力标准差随含沙量的变化规律与文献[14]中水流的脉动压力随含沙量的变化规律是相通的。

实际上，泥沙对水流紊动的影响因素中，使紊动增加与使紊动减小的因素同时存在。一般来说，以推移质形式存在的泥沙颗粒，会有更多的机会与边壁碰撞摩擦，降低了水流稳定性，使紊动增强；以絮网结构存在的泥沙，会给水流中涡体的产生与混掺造成困难，使紊动减弱。在不同含沙量条件下，水流紊动强度取决于两种作用的对比消长结果，在本试验中，含沙量小于183 kg/m3时，使紊动增强的因素占主导地位，含沙量大于183 kg/m3时，使紊动减弱的因素占主导地位。以往与水流含沙量有关的试验，如文献[16]中孔板泄洪洞内的脉动壁压及文献[17]砂粒对空化空蚀的影响研究中，都发现了存在临界含沙量这一现象，但因泥沙问题较为复杂，不同试验中临界含沙量值可能存在较大差异，目前的研究水平仍难以完全做到定量表达，因此这里主要从定性上分析了泥沙含量影响水流紊动时存在临界含沙量的原因。

2.3 最大上举力与水力条件的关系

工程上一般从结构角度出发，评估瞬时最大脉动上举力对底板稳定性的影响，即考虑在某一瞬时，作用在底板上表面的动水压强最小而下表面的动水压强最大的情况，这一瞬间的上举力大小可以作为底板稳定性研究的控制标准，因此有必要对不同水力条件下的最大上举力进行分析。由上举力的形成机理可知，影响最大上举力Fmax的物理量主要有射流速度u、水垫塘水深h、水体密度ρ、底板块宽度l、射流入射角度θ、水体含沙颗粒的中值粒径d等。由于本试验所用泥沙为同种中值粒径，且射流水舌基本垂直入水，这里暂不计d、θ的影响，因此，最大上举力可以表示为

Fmax=f(u,h,ρ,g,l)

(1)

根据本文的模型试验，对式(1)进行无量纲分析得：

(2)

式(2)等号左边表示底板块单位面积所受的最大上举力Fmax/l2与浮托力ρgh的比值，等号右边表示水垫塘内与水力条件有关的佛劳德数Fr。图8显示了4号板块Fmax/(ρghl2)与Fr的关系。

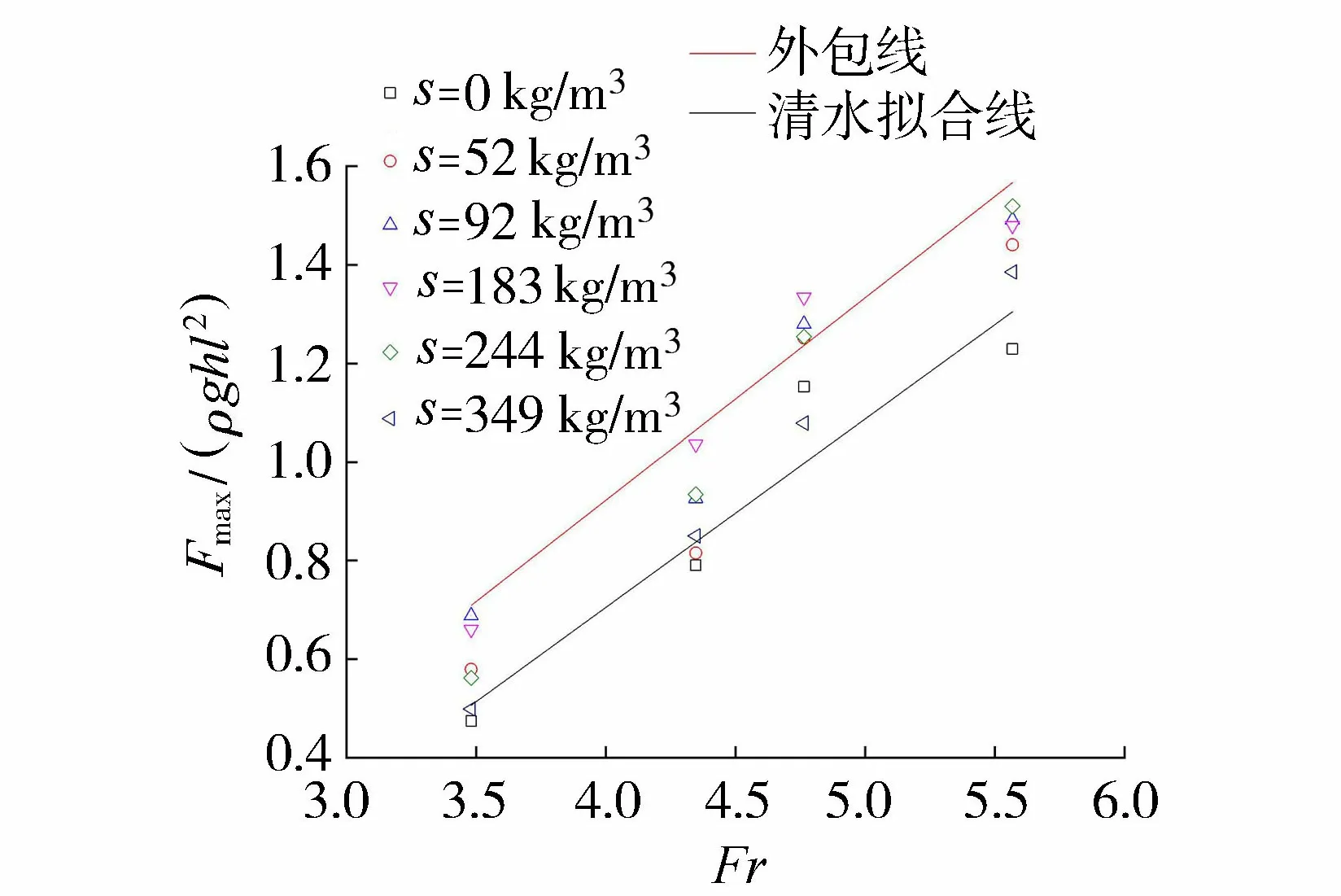
图8 Fmax/(ρghl2)与Fr的关系

出于安全考虑，图8中给出了各工况下最大上举力的外包线，其方程为

(3)

为了与清水条件下的最大上举力进行对比，图8中还作出了清水(含沙量为0 kg/m3)时各水力条件下数据的拟合线，其方程为

(4)

由式(3)(4)可以估算在本试验范围内的其他水力条件下，水流含沙后引起最大上举力与清水相比增加的幅度，当Fr=3.5时，增幅为40%，当Fr=5.6时，增幅为20%。这可以为进一步深化研究提供一定的参考作用。

图9给出了Fr不同时无量纲化的最大上举力与含沙量之间的关系，可知，同一Fr条件下，随含沙量的增大，无量纲化的最大上举力呈先增大后减小的趋势，这与上举力标准差随含沙量变化的趋势相似。

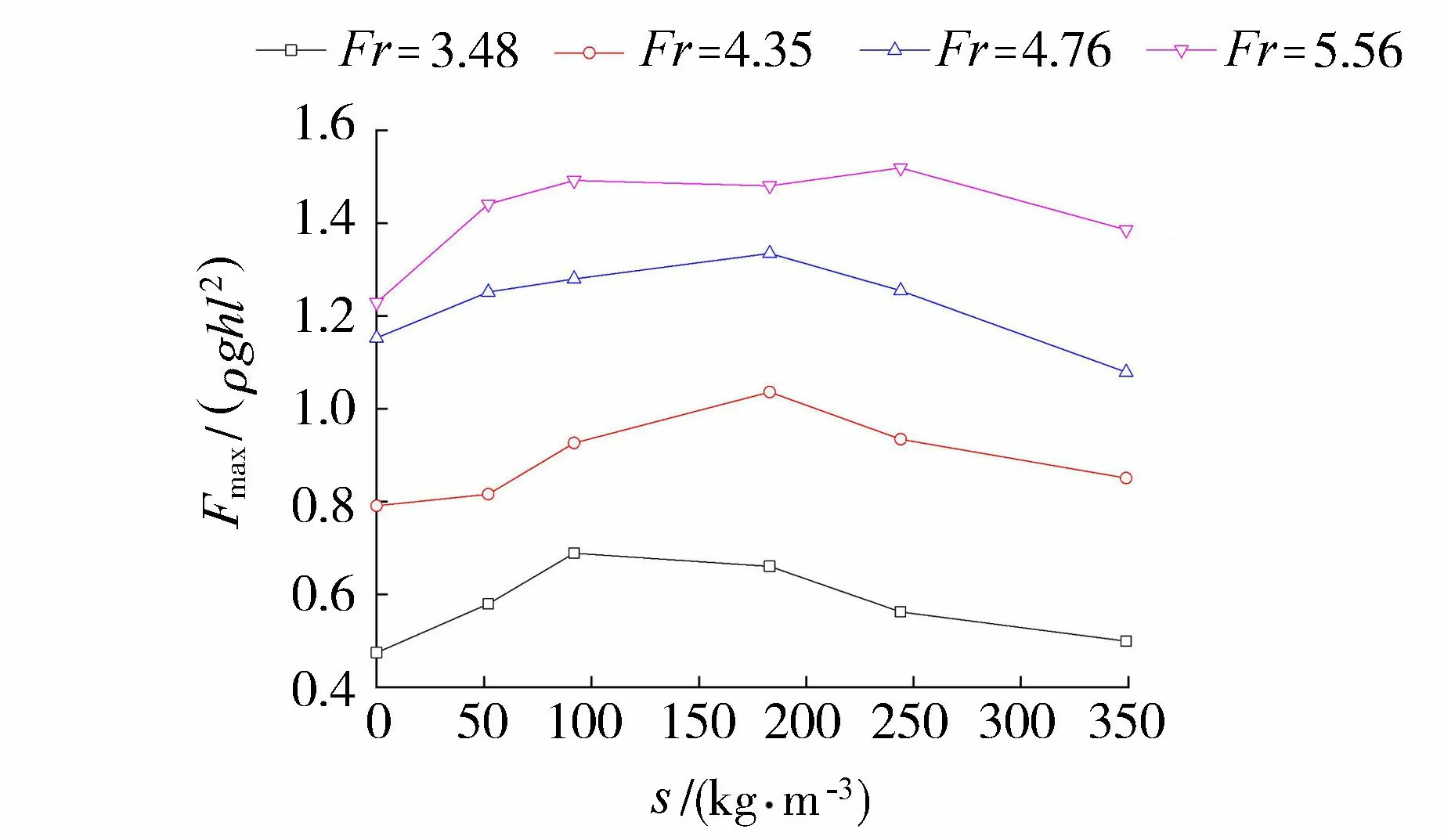
图9 Fmax/(ρghl2)与s的关系

2.4 上举力频谱特性及时间相关特性

采用功率谱密度函数分析上举力在频域内的特性。在射流速度为13.50 m/s条件下，4号板块在不同含沙量情况下的归一化功率谱如图10所示。由图10可知，板块所受上举力主频在0～3 Hz范围内，功率谱密度在6 Hz以内基本衰减至零点附近，低频域内的脉动能量占主要部分，说明水垫塘中底板上举力的脉动属于低频大幅脉动；增加泥沙后，底板上举力脉动过程仍然以低频为主，但随着含沙量的增加，频带宽度逐渐增大，高频域内的功率谱密度值也有所增加，说明水流含沙后引起底板上举力脉动的涡旋尺度的变化更加复杂，存在较高频率脉动能量的作用，使底板产生高频小尺度的振动，持续作用下可能引起底板松动，在一定程度上为底板的出穴提供了条件，降低了底板稳定性。

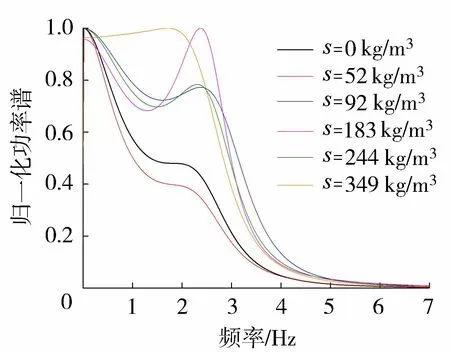
图10 u=13.50 m/s时4号板块归一化功率谱

为了分析涡旋尺度随含沙量的变化情况，采用由脉动荷载的自相关函数得到的时间积分尺度来表示涡旋尺度[18]。图11给出了4号板块时间积分尺度与含沙量的关系。由图11可知，4号板块时间积分尺度随着含沙量的增大呈先增大后减小的趋势，且在临界含沙量183 kg/m3处取得最大值。可以认为，水流含沙后，尤其是含沙量超过183 kg/m3后，会出现更多小尺度的涡旋结构，使时间积分尺度较清水时更小。

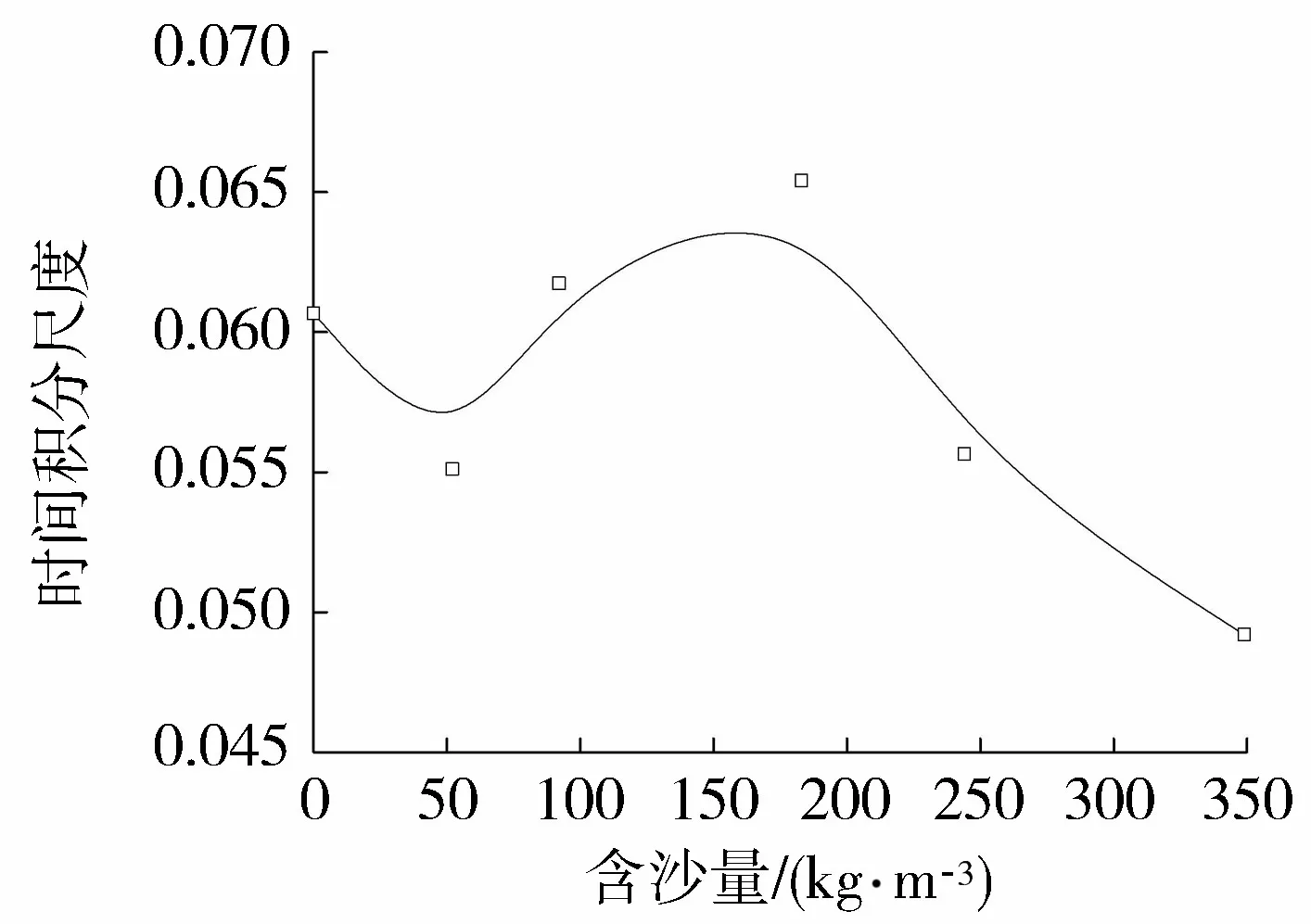
图11 4号板块时间积分尺度与含沙量关系

3 结 论

a. 在不同含沙量水流下，水垫塘底板上举力时均值、标准差、最大值的分布规律均与清水条件下的分布规律相似。上举力时均值与上举力最大值在射流直接冲击的板块处取得沿程最小值，在与冲击点相邻的板块处取得最大值；上举力标准差在射流冲击的板块处取得最大值，随后向上下游两侧逐渐下降至零值附近。

b. 随着含沙量的增加，水垫塘内各板块所受的上举力时均值均有不同程度的增加，而上举力标准差先增大后减小，在临界含沙量183 kg/m3处取得最大值。

c. 不同含沙量下水垫塘底板上举力的脉动都在低频范围内，但与清水对比，水流含沙后的频带宽度有所增加，高频域内的功率谱密度值有所增加；水流的时间积分尺度随着含沙量的增大呈先增大后减小的趋势。