基于时间线段树的城市可达区域搜索
孙鹤立,张优优,杨 洲,何 亮,贾晓琳
(西安交通大学计算机科学与技术学院,西安 710049)
(*通信作者电子邮箱xlinjia@xjtu.edu.cn)
0 引言
近年来,随着智慧城市的快速发展,城市计算的概念被提出并很快受到了极大的关注。城市可达区域搜索是城市计算中基于位置的最重要的服务之一,可在用户指定的空间位置和时间间隔等条件下,根据大量的轨迹数据[1]挖掘出特定路段。它对于许多城市应用具有重要的意义,如基于位置的推荐、基于位置的广告、商业覆盖分析等。
Jeung 等[2]于2010 年提出了基于预测线路的方法来进行城市区域查询。同年,Zhang 等[3]提出了基于闵科夫斯基和与k最近邻(k-Nearest Neighbor,kNN)算法进行区域查询。2015 年,Li 等[4]提出了一种基于采样的方法获取用户指定区域的轨迹数目。Li 等[5]和Alarabi[6]提出了在大量轨迹中的高效管理查询方法。除此之外,针对可达性查询问题也开展了一些相关工作。可达性查询是指查询在图中的两个节点之间是否存在一条通路,这是其他许多应用的基本问题。Chen等[7-8]和van Schaik 等[9]提出了多种高效的方法来解决图可达查询问题。此外,Bramandia 等[10]和Cai 等[11]还引入了两跳标记模式来解决查询问题,并提出了一些启发式方法来减小标签的大小。Du 等[12]引入了k跳改进了两跳标记模式方法。Seufert 等[13]和Veloso 等[14]提出构造一个小索引,以较小的构造成本来解决可达性查询。以上这些传统的图可达性查询方法主要集中在静态图结构上[15-16],而不是像轨迹这样与图结构相关联的动态数据。与这些查询不同,Anastasiou等[17]提出了数据驱动的可达性分析方法。Wu 等[18]提出了单点上下界限区域可达查询(Single-location reachability Query Maximum/minimum Bounding region search,SQMB)方法,时空可达性查询结果依赖于查询时间且查询速度较快,但是在实际大规模应用中,该方法仍会存在查询效率和查询准确率低下的问题。
针对以上问题,本文提出一种基于时间线段树的城市可达区域搜索tst_search(urban reachable region search based on time segment tree)算法,主要包括:道路的概率时间权重生成、层级跳跃表的生成与存储、构建时间线段树索引结构和道路网络迭代搜索4 个步骤。实验结果表明,与现有方法相比,本文提出的可达区域搜索方法具有更高的效率与准确率。
本文的主要工作如下:
1)提出了基于道路速度分布模型的概率时间权重计算方法;
2)设计了存储局部可达区的层级跳跃表和时间线段树,提高了算法搜索效率;
3)提出了动态自适应的可达区域搜索算法,提高了搜索准确率。
1 城市可达区域搜索框架
1.1 基本概念
定义1道路网络。道路网络RN可以被视为有向图G=(V,R),其中V={v1,v2,…,vm}是交叉口的集合,R={r1,r2,…,rn}是路段的集合。
定义2轨迹。轨迹Tr是时间有序的序列Tr={p1,p2,…,pn},其中每个点pi=(lati,lngi,ti),1 ≤i≤n,pi是包含经度lngi、纬度lati和时间戳ti的全球定位系统(Global Positioning System,GPS)记录。
定义3可达性。给定起始位置S,起始时间T,行程时间L,道路网络中的路段ri,如果由历史轨迹生成的带时间权重的道路网络中存在一条通路,在给定的行程时间L之内从起始位置穿过给定路段,则可达,否则不可达。可达性具体表示为:
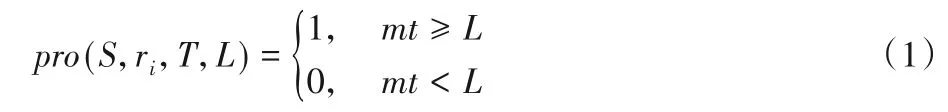
其中:mt为S在T时刻的到ri的最小时间间隔。
定义4可达区域。给定起始位置S,起始时间T,行程时间L,可达区域是一组包含所有从S开始的可达路段。可达区域的具体表示为:
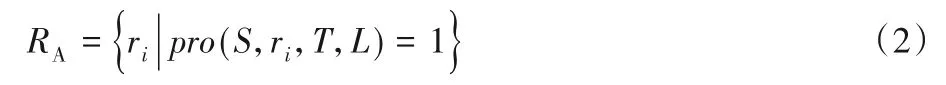
定义5概率速度vp。给定道路网络中某条路段的历史速度分布函数f(v),累积分布函数F(v),概率p,那么概率速度vp是指使P(v>vlim)=1-F(v)=p的速度vlim。具体表示为:

定义6概率可达区域。概率可达区域是可达区域更一般的描述,可达概率描述了历史轨迹数据集中支持在给定行程时间内从S可达路段ri这一事实的概率速度对应的置信度。
1.2 问题定义
给定道路网络G(V,R),起始位置S,起始时间T,行程时间L,置信度P,轨迹数据库Tr,查询某路段集合作为G中的概率可达区域,使得区域中的路段都至少能在给定的行程时间内从起始位置S到达。
1.3 整体框架
本文方法使用了高效的数据结构和动态的自适应搜索算法,使得城市可达区域的查询既快速又准确。整体方案框架如图1 所示,主要包括4 个环节:1)进行轨迹与道路的地图匹配,根据道路速度分布模型生成道路段的概率时间权重;2)利用层级跳跃表算法生成多时间粒度的局部可达区域集合,并进行短时间可达区域存储;3)利用时间线段树对层级跳跃表所存储的多时间粒度可达区域建立高效的层次树状索引结构;4)使用时间线段树索引在道路网络中进行迭代搜索,最终输出可达区域集合。
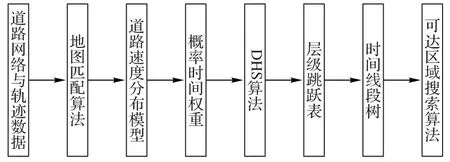
图1 可达区域搜索框架Fig.1 Framework of reachable region search
2 城市可达区域搜索算法
2.1 道路概率时间权重生成
首先使用地图匹配算法将轨迹数据映射到道路网络中[19],得到各条城市道路段对应的历史轨迹。然后将历史轨迹在时间维度上进行分箱,这里以10 min为间隔,根据历史轨迹计算短时间间隔内道路的平均速度和速度方差,如图2所示。
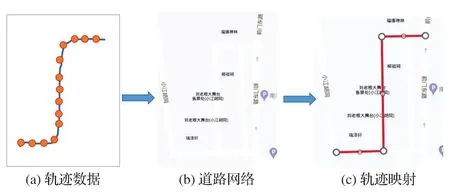
图2 地图匹配Fig.2 Map matching
通过卡方检验等数据检验方法发现,道路的速度分布满足对数正态分布[20-21]。概率密度函数为:

其中:μ与σ分别是变量对数的平均值与标准差。根据平均速度E(v)与方差D(v),可以通过以下两式求得μ与σ的值:
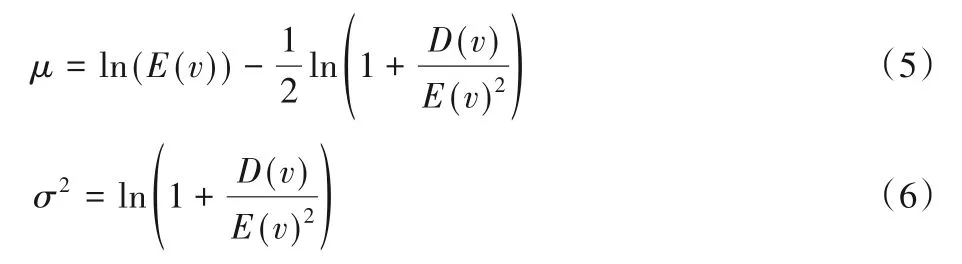
得到了道路段的速度分布模型后,根据概率速度的定义即可生成不同置信度对应的速度,进而生成道路的概率时间权重。
2.2 层级跳跃表生成算法
由于城市道路网络的规模较大,在道路网络中直接使用贪心搜索算法会导致搜索效率低下,因此,本文提出了层级跳跃表(Hierarchical Skip List,HSL)生成算法,该算法通过生成多时间粒度而非单一时间粒度的局部可达区域集合,并进行短时间可达区域信息的存储来提升长时间查询的效率与准确率。具体来说,本文设计的HSL 算法引入了层级跳跃表中的时间粒度约束。在算法迭代的过程中,当道路网络中从某路段起始的可达路径的时间间隔超过附加的时间约束时,如果继续执行网络扩张算法,可达时间超过行程时间间隔的可达路段会在存储时丢弃,属于冗余信息,因此算法会提前终止。算法1展示了层级跳跃表生成的具体过程。

层级跳跃表如图3 所示,记录了任意一条路段在连续时间间隔T1-T2、T2-T3、T3-T4 内可以到达的路段。当所有的层级跳跃表都计算并存储完毕时,对于用户输入的某行程时间L,在搜索的开始阶段可以利用层级跳跃表快速地进行粗粒度时间的路网扩张搜索,在搜索过程接近尾声时,层级跳跃表可以适应细粒度时间的搜索要求,使搜索结果更加准确。
2.3 时间线段树索引构建
若直接在层级跳跃表上进行可达区域搜索,在高频次搜索情况下,可达区域搜索仍然存在低效的问题。因此,在获得了道路的层级跳跃表之后,在其基础上构建时间线段树索引来进一步提升查询效率。
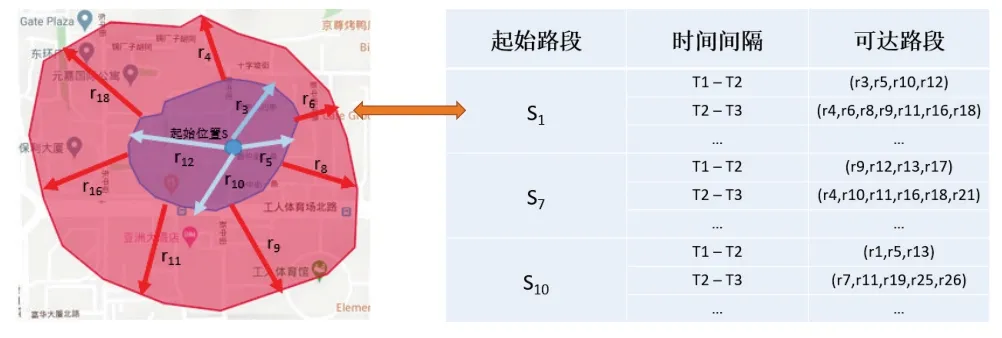
图3 层级跳跃表Fig.3 Hierarchical skip list
如图4 所示,时间线段树的基本结构是一棵二叉搜索树,它存储的是不同时间间隔的可达区域信息,每个节点包含以下信息:时间间隔的起始时刻和终止时刻;每个时间间隔内可达区域集合。以节点1 为例,1∶0-1 的含义是时间线段树索引为1 的节点存储了时间间隔索引0 到1 的可达区域信息,该区域信息可由节点1 的左孩子节点3 和右孩子节点4 得到,其中节点3 维护的时间间隔索引0 的可达区域信息,同理,节点4维护的时间间隔索引1 的可达区域信息。由于时间线段树存储了多时间间隔的可达区域信息,在可达区域搜索的过程中,本文算法会根据行程时间自动调整当前搜索的时间间隔,以适应不同的搜索条件。
时间线段树索引的操作主要有两个:构建与查询。时间线段树索引的构建过程如下:1)对于每一个树节点,确定其起始与终止时间索引的范围;2)若节点为叶子节点,保存该节点时间索引所维护的区域信息,否则递归建立以左右孩子为根节点的时间线段树;3)递归返回时合并各个孩子节点所保存的区域信息,从而完成整棵树的建立。
当时间线段树构建完成后,线段树中的各个节点分别存储了不同长短时间间隔对应的可达区域(道路段)信息。以图4 为例,假设层级跳跃表中存储了以下信息:从某起始路段r0出发在0~1,1~2,…,3~4 min 内到达的区域分别为A1、A2、A3、A4,那么时间线段树构建完成后,叶子节点3、4、5、6存储的可达区域分别为A1、A2、A3、A4,节点1、2 存储的可达区域分别为A1∪A2,A3∪A4,根节点0存储的可达区域为A1∪A2∪A3∪A4。
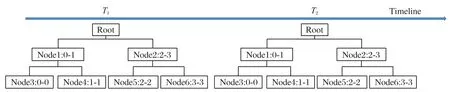
图4 时间线段树Fig.4 Time segment tree
2.4 可达区域搜索算法
可达区域搜索算法以时间线段树索引为基础,根据搜索输入的概率P,起始位置S,起始时刻T,行程时间L来输出可达区域的路段集合。首先,介绍时间线段树索引查询过程:1)若查询时间区间与根节点时间区间相等,直接返回根节点维护的区域信息即可,否则根据查询区间与左右孩子节点的关系递归在左子树或者右子树中搜索;2)递归返回过程中对两个孩子节点的区域信息进行合并并返回。
然后,对于城市可达区域搜索的整个过程,具体步骤如下:首先初始化可达区域,然后根据时间线段树索引查询当前时刻T可达区域中所有路段扩展的区域,并动态更新区域内所有路段的剩余权重,之后,更新可达区域,迭代上述过程直到所有路段的剩余权重为零时算法终止。算法2 展示了可达区域搜索的具体过程。

具体流程如下:
1)初始化可达区域。使用起始位置S对可达区域进行初始化,并将S的剩余时间remainder初始化为L;
2)扩增可达区域。根据时间线段树和路段ri的剩余时间remainderi查询当前可达区域中所有路段ri的局部可达区域,扩增当前可达区域并根据ri与其局部可达区域之间的行程时间ti更新所有可达路段的剩余时间remainderi,具体地,若某路段ri的剩余时间remainderi,根据时间线段树查询其局部可达区域中某路段rj距离ri的行程时间为ti,那么将rj扩增为当前可达区域后,rj的剩余时间更新为remainderi-ti;
3)循环步骤2)直至所有可达路段的剩余时间为零,输出可达区域。
3 实验与结果分析
3.1 实验环境与数据集
在本研究过程中,实验环境为64 位Windows 10,Intel Core i5-4590,3.30 GHz 四核CPU,8 GB 内存。主要使用了两类数据集[22-24]:地图网络数据和轨迹数据。地图网络数据使用了北京市的路网数据,包括196 307 条道路和148 110 个路口;轨迹数据是由北京市上万辆出租车从2013 年9 月1 日—10 月31 号2 个月内所产生的,包括673 469 757 个GPS 点,总长度达到26 218 407 km。
3.2 评价指标
为验证算法在城市可达区域搜索中的性能,使用运行时间和准确率来评价算法。设穷举算法的可达区域集合为Se,其他算法搜索所得的可达区域集合为Sa,那么,本文定义两者的Jaccard系数为该算法的准确率:

从式(7)可看出,被评价算法的可达区域集合与穷举算法的可达区域集合交集数量与并集数量之比即为被评价算法的准确率。
3.3 层级跳跃表生成的效率比较
图5 展示了在层级跳跃表的生成过程中使用了时间粒度约束后,本文的HSL 算法相较于基准的贪心算法DH(Dijkstra with Heap)的运行效率。
由图5 可知,相较于DH 算法,本文提出的HSL 算法在p=0.6,0.7,0.8 等不同查询概率下,本文算法的运行时间均小于DH 算法。分析其原因,DH 算法在网络扩张过程中只有单一的网络大小条件约束,而HSL 算法加入了新的时间维度的约束,使得算法避免在全局网络中进行搜索,而仅仅在包含结果的局部网络中迭代扩增,因此,本文算法效率大幅提升。
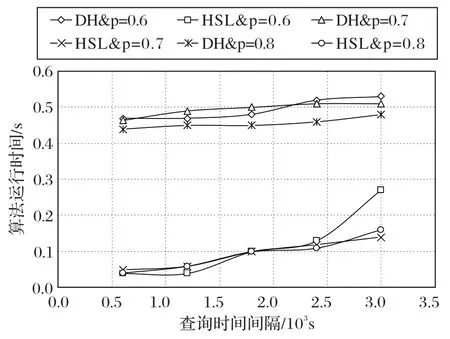
图5 层级跳跃表生成的效率比较Fig.5 Efficiency comparison of generation of hierarchical skip list
3.4 可达区域搜索的效率比较
与最新的研究一致,将基准方法设置为穷举搜索es_search(exhaustive search),该算法通过在道路网络中不断搜索相邻路段来获取可达区域[18]。除此之外,还对比了目前最新的连接表搜索(search based on connection table,con_table_search)算法[18]和tst_search,以验证本文算法的高效性和准确性。
图6 展示了不同行程时间对算法运行时间的影响。其中,图6(a)表示的是Δt=400,p=0.6 条件下各种算法效率对比,由实验结果可知es_search 算法的运行时间稳定在34 s 左右,con_table_seach 与tst_search 算法的运行时间随着行程时间的增加而增加,但是即使在行程时间长达1 h 的条件下,这两个算法的运行时间依然远小于es_search,且本文的tst_search 算法运行时间总低于con_table_seach。此外,为了验证不同参数对实验结果的影响,本文针对不同的线段树时间间隔和查询概率进行了大量实验。图6(b)~(f)分别表示了在其他5 种不同条件下,3 种算法运行时间的对比。不难发现,本文tst_search 算法效率依然高于其他两种算法。分析其原因,tst_search 使用了线段树在时间区间上存储的局部可达区域信息,可以快速地查找某时间间隔内可达区域的集合。相较于直接查找,线段树的查找时间复杂度为O(logN),在数据量较大的情况下,查询效率远高于时间复杂度为O(N)的直接查找。除此之外,多层跳跃表的设计也扩增了跳跃搜索的最大时间间隔,允许算法在更大范围上进行快速迭代,减少算法的运行时间。
3.5 可达区域搜索的准确率比较
不同算法的准确率如图7 所示。由实验结果可知,本文提出的tst_search 算法的准确率在不同行程时间不同查询概率的情况下均远高于con_table_search 算法,分析其原因,con_table_search 算法在地图网络中迭代搜索时,不管起始位置到中间路段的具体时间值,均在下次迭代时将查询时间削减一个定值,即连接表的最大时间间隔。而本文提出的tst_search 动态地记录了每条路段的时间权重,能较准确地查询出可达区域结果。此外,本文线段树的层级设计结构在算法即将终止时能在细粒度时间上搜索,也对可达区域的准确性有益。
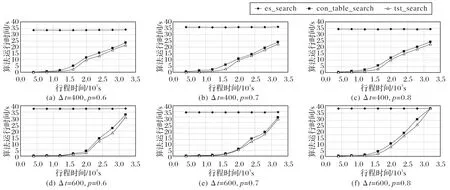
图6 不同行程时间的效率比较Fig.6 Efficiency comparison of different travel times
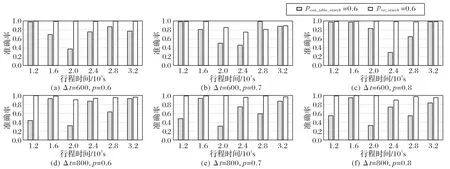
图7 不同行程时间的准确率比较Fig.7 Accuracy comparison of different travel times
4 结语
本文提出了一种根据用户指定的条件在城市中搜索可达区域的方法。该方法通过道路的概率时间权重生成、层级跳跃表的生成与存储、构建时间线段树索引结构、道路网络迭代搜索等四个环节,完成城市可达区域搜索过程。本文方法使用了时间线段树索引,将局部可达信息提前存储起来,并且使用了动态自适应的迭代搜索策略,在保证高效的前提下尽可能减小搜索结果的错误。实验结果表明,本文方法与现有方法相比,城市可达区域的搜索既高效又准确。在接下来的工作中,将研究多个起始位置情况下的可达区域搜索问题,以便为复杂场景下的应用提供思路。

