负载影响下纯电动汽车配送路径规划及充电策略

刘育良，陈淮莉

（上海海事大学物流科学与工程研究院，上海 201306）

（*通信作者电子邮箱1487630534@qq.com）

0 引言

随着城市化进程的加快，人们对城市生活的质量也提出了高要求，城市配送物流作为城市生活的重要组成部分之一，配送方式的完善将会有助于城市生活质量的改进。电动汽车在城市配送物流中的应用越来越受到关注，其中以深圳作为首要的代表，连续三年成为纯电动物流汽车保有量最大的城市，为绿色的城市物流作出了贡献。

城市物流配送的问题，就是传统的车辆路径规划问题，但由于电动汽车需要在充电站进行充电，而且充电时间是一个不容忽略的因素，所以纯电动汽车应用在城市物流配送中具有其特殊的性质。对于纯电动汽车在城市物流配送中的应用研究，Keskin 等［1］将其描述为一个带时间窗的路径规划问题，建立了混合整数线性规划模型，考虑排队充电问题和偏离时间窗的惩罚成本，运用数学优化技术CPLEX（WebSphere ILOG CPLEX）来求解小实例。Madankumar等［2］把它作为一种绿色物流，研究了配送及集货的路径规划问题。van Heeswijk等［3］将其描述为带时间窗的配送问题，建立了配送模型。Schneider 等［4］将其描述为带有时间窗和充电站的问题，考虑了有限的车辆货运能力以及客户时间窗，提出了一种混合启发式算法，它结合了变量邻域搜索算法和禁忌搜索启发式算法，进行了相关问题的实例测试。Barth 等［5］建立了车辆负载与能耗影响的函数关系，Kancharla 等［6］则在此基础上考虑了负载对纯电动汽车路径的影响，建立了距离最小化的模型，建立了考虑负载消耗的功率估计函数，并提出了一种具有特殊算子的自适应大邻域搜索算法。苏粟等［7］也考虑了实时动态能耗的影响，研究了纯电动汽车充电路径规划，发现考虑实时动态能耗，能够制定更合理的充电策略。

对纯电动汽车在城市物流配送中的研究，设置不同的目标会使计算的结果有所差异。Schiffer等［8］则提出了一个不同的目标函数，不仅最小化了行驶距离，还最小化了所需的车辆、设置的充电站数量以及总成本。他认为如果可以将充电桩选址与车辆的路径规划相结合，会得到更优的结果，该目标函数的设置相对来说更符合企业的需求。贾永基等［9］针对多目标独占性电动汽车路径问题，提出了基于时间敏感系数的客户满意度评价函数，时间敏感系数体现了客户对未能在指定的时间窗口内得到服务的容忍程度。该研究把客户的满意程度量化，以实现客户的最大满意度为目标。Schneider 等［10］在考虑交换服务需求不确定性和电能价格不确定性的情况下，计算单站和交换站网络的最优设备配置，提出了一个针对小问题的最优解算法和一个基于动态规划和蒙特卡罗采样的近似算法，为充电作业进行了合理的安排设置。Zhang 等［11］建立了能量消耗最小化的目标函数，并验证了以能量消耗最低的优越性。

考虑纯电动汽车中途充电的问题，可以根据设定的路线安排充电任务，但是对于何时充电，充多少电，也是本领域内研究的一个问题。传统的研究是考虑在电池的电量低于某个设定值时再充电，这就需要车辆停留一段较长的时间来进行充电任务。但Keskin 等［12］放宽了完全充电限制，允许车辆部分充电，由于充电时间较短，在现实生活中更为实用。Sweda［13］也建立了纯电动车辆在充电策略的模型，但是在现有电池技术的情况下，允许部分充电对电池的损耗程度较大，这项研究没有考虑电池的损耗成本。郭放等［14］指出，当电池进行深度放电之后，对电池的损耗程度会加深，降低电池的使用寿命。目前，在我国市面上的纯电动汽车多采用三元锂电池，这种电池的特性决定了潜在的充电成本。所以，物流企业在安排配送路线以及充电策略时要考虑部分充电对电池带来的损耗成本。

在配送模型的求解上，梁承姬等［15］采用改进遗传算法（Genetic Algorithm，GA）求解，提高了求解速度，快速获得一个较优的解。Zhang 等［16］设计了蚁群（Ant Colony Optimization，ACO）算法进行求解，发现蚁群算法在求解此类问题时具有良好的特性。冯杰等［17］也采用蚁群算法求解了生鲜品的配送问题，并与遗传算法和粒子群算法进行比较，验证了蚁群算法在求解路径规划问题时的优越性。

以上文献对于该问题的研究，并未针对城市物流中的多批次、更细化的时间窗进行解决，并且，单个车辆一般都是在一天中出车一次，并未研究循环多次出车中充电任务的安排。另外，这些研究大都把车辆的电量消耗设定为一个稳定的值，其实负载对车辆电量的消耗有着密切的联系。本文考虑实时负载对电池输出功率的影响，更准确地计算电量的损耗，并针对细化的时间窗，考虑多次循环出车的路径规划和充电策略。

1 问题描述

城市物流配送是一个很常见的问题，随着城市化进行的加快发展，城市物流的合理化运营，有助于缓解城市交通压力。近些年，纯电动汽车在技术上的发展取得了一定的成果，这为纯电动汽车实现商用奠定了基础。例如城市公交车，大多都采用了纯电动汽车实现了运营，这不仅减少了城市污染气体的排放，更降低了城市的噪声污染，为城市生活品质的提升作出了贡献。如果城市物流配送任务可以大规模使用纯电动汽车来进行运营，这对城市生活的改进将会是很明显的

一般对城市物流配送的研究都是采用燃油车进行配送，由于燃油车当燃料用尽时，很快就能进行补充，对配送任务的时间影响程度很小。但由于纯电动汽车的电量是有限的，进行电量补充需要较长的时间，这就对后续的配送任务有较大的影响，尤其是在满足顾客需求时间窗这一方面更加需要合理的调度。在纯电动汽车配送领域内，普遍的研究并没有考虑货载重量对车辆耗电的影响。在车辆负载不同时，传统的内燃机油耗变化范围较小，而纯电动货车电池耗电情况变化相对较大，由于在配送过程中，车辆的负载在经过每一客户点时都发生变化，所以纯电动车辆的负载影响不能忽略。本文参考了文献［6］中提到的货载对车辆实时耗电的影响，公式如下：

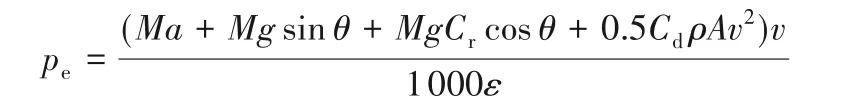
本文假定车辆保持匀速在平直的道路上行驶，公式如下：

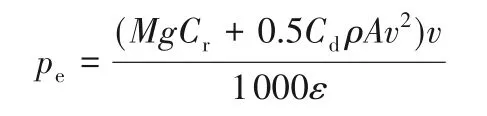
简化后为：

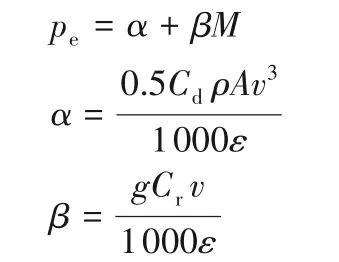
其中：M为车的整体质量，包含车重m（单位：kg）和车上的货物重量μ；v表示车辆行驶的速度（单位：km/h）；a表示车辆的加速度；g表示重力常量；θ为道路坡度角（单位：度）；ρ为空气密度（单位：kg/m3）；A为迎面面积（单位：m2）；Cd为空气动力阻力系数；Cr为滚动阻力系数；ε为车辆传动系效率；pe是连续的发动机功率输出（单位：kW）。具体的参数设置如表1所示。

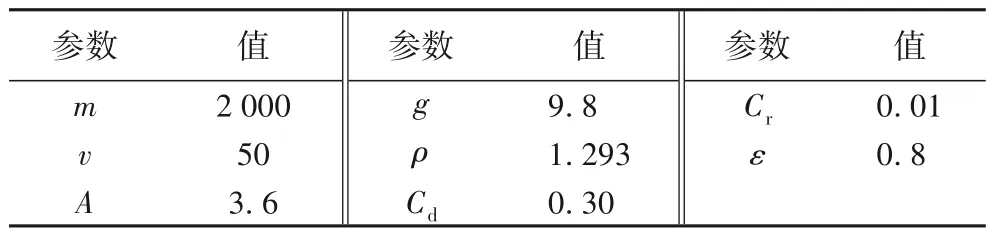
表1 能耗公式参数Tab.1 Energy consumption formula parameters

另外，对纯电动汽车配送的研究中，很少有安排车辆多次循环出车的情况。由于城市面积有一定的限制，纯电动汽车的行驶里程最多大约可以达到220 km，单次出车大多时候可以在配送任务完成之后进行充电，这同时就会加大纯电动汽车的运营成本。本文考虑了多个客户在一天内的需求由少量的纯电动汽车循环进行配送，当车辆完成一次配送之后，返回配送中心装载下一次配送的货物，同时要考虑中途可能在某一点进行充电，尽可能避免与客户的需求时间窗冲突，提高配送的时间准确性。考虑负载对能耗的影响，可以更加准确地安排运营计划。为满足充电的需求，文中假设有10 个充电站分布在该区域内，采用快速充电的方式为纯电动汽车提供充电服务。

2 模型建立

2.1 参数定义

模型中各个参数的含义如下：

m表示车重；

μj表示到达客户j时车的负载量；

xijk表示车辆从i到j且由车辆k来完成任务；

K表示车辆的集合；

τi表示车辆到达i点的时刻；

tij表示车辆从i到j的时间；

si表示车辆在i点的服务时间（卸货时间）；

yi表示站点i的货物需求量；

τj表示车辆到j点的时刻；

η表示充电时间关于充电量的比率系数；

N表示充电的次数；

Q表示电池的总电量；

qi表示在i点时的剩余电量；

ej表示到达j的最早时刻；

lj表示到达j的最晚时刻；

Z表示车辆的最大负载量；

Δit表示表示客户i的货物的运输时间；

Δid表示表示客户i的货物的运输距离；

χ表示运输时间的比例系数；

ω表示运输距离的比例系数。

2.2 模型建立

式（1）为目标函数，表示企业当天的运营成本最小。

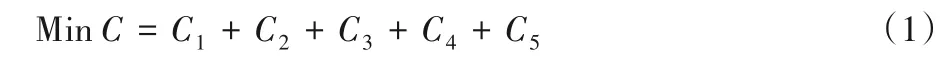
当天的运营成本分为五个部分：

C1表示一个车辆当天配备司机的人工成本，Ck1为一个常量，取值为200。计算公式如下：

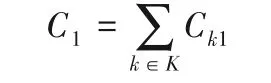
C2表示一个车辆的变动运输成本系数，Ck2是一个常量，取值0.3。该成本包括车辆的维修、变动的保养费用等。这些费用是与车辆的行驶里程成正比关系的，随着车辆行驶里程的增加而增加。计算公式如下：

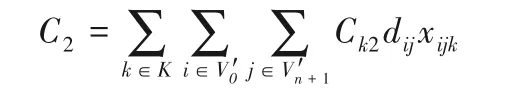
C3表示每单位电量的价格，Ck3是一个常量，取值为1。该成本包括汽车中途的充电成本以及返回配送中心之后充满的成本。计算公式如下：

C4表示货损成本，货损是指在货物在运输过程中产生的损耗，由于货物的种类不同，货损的程度也不一样。对于易碎品、生鲜品等，货损量会较普通货物多一些。本文参考文献［3］，设定随着运输时间和运输距离的增加，货损成本随之增加，Ck4是一个常量，取0.1；χ和ω取值分别为0.4 和0.6。计算公式如下：

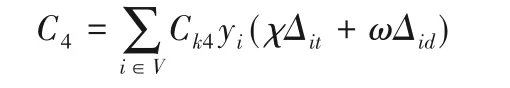
C5表示车辆的惩罚成本。由于现实中临时突发状况的影响，如堵车、道路维护、调度失误等情况的发生，加入惩罚成本。当车辆在客户最早服务时间之前到达时，产生等待成本，惩罚因子ch设为12 元/小时。超出最迟服务时间时，设惩罚成本Mp为无限大，保证必须满足客户的服务要求。计算公式如下：

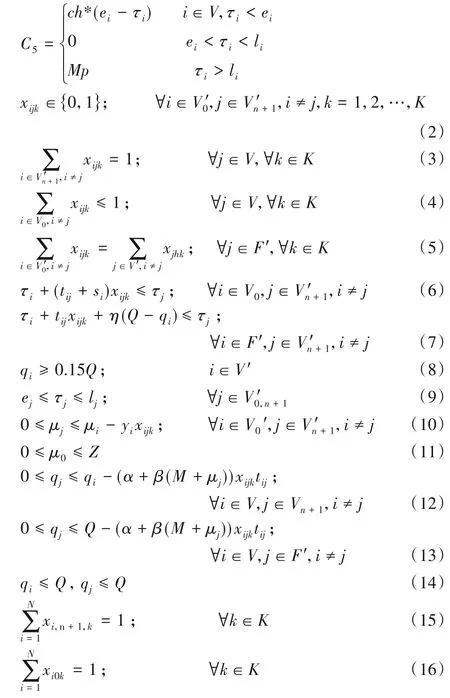
式（2）表示xijk为一个0-1 变量，若车辆k从i到j则为1，否则为0；

式（3）表示每一个客户的订单任务都要完成；

式（4）表示充电站最多被访问一次；

式（5）表示每个节点进入的车辆和离开的车辆数量相等；

式（6）和（7）表示车辆到达i的时刻要小于到达j的时刻；

式（8）表示车辆在每个客户点时，车辆剩余电量不能低于总电量的15%；

式（9）表示车辆要在客户需求时间窗内完成配送任务；

式（10）表示车辆在j点时的负载量小于在i点时的负载量；

式（11）表示车辆的负载量在零和最大负载量之间；

式（12）至（14）是对到达j时的剩余电量的约束，不能大于在i的剩余电量，并且都不能大于总电量；

式（15）表示车辆k在完成单次任务之后返回配送中心，装载下一次配送的货物；

式（16）表示车辆k在完成一天的任务之后返回配送中心，结束当天配送任务。

3 算法设计

本文所研究的问题是传统的路径规划问题的延伸，由于电动汽车需要充电且充电时长不可忽略的特点，在有时间窗约束情况下的路径规划就会比较复杂。再者，纯电动汽车在不同负载情况下的能量消耗较燃油车更为明显。所以，对纯电动汽车的负载与能耗关系的考虑，可以更加准确地计算车辆的能耗情况，合理安排下一阶段的任务分配情况。蚁群算法在求解路径规划问题时采用正向反馈、启发式搜索的特性，大幅提高了求解的效率。

本文设计的蚁群算法考虑了时间窗的约束，加入了时间紧迫因子，最大限度地保证车辆满足客户服务时间窗。在进行下一客户点的选择时，车上已载货物与下一站点客户需求之和不能大于车辆最大负载，到达下一站点的电量不能低于总电量的15%，以此来限制蚂蚁的选择范围。在蚂蚁的单次旅行中，负载量由配送中心开始为最大，每访问一个客户，负载减小，到达后一站点的负载量始终小于在前一站点的负载量。在当天配送任务开始时，蚂蚁在配送中心处的电量为100%，车辆的电量在到达充电站之前，电量逐渐减少，在每一客户站点比前一站点电量低。蚂蚁在完成单次配送任务返回配送中心后，负载量由0 变为下次配送任务的总货量，进行下一次配送任务。

蚁群算法中两个重要的因素为转移概率和信息素更新，转移概率用来设定蚂蚁选择下一站点的选择规则，信息素更新机制决定蚂蚁选择路线的概率，以下结合实际问题作出相应设置，并给出了算法的具体流程。

3.1 转移概率

转移概率函数的设置是路径规划的重要因素，对客户点的选择起着重要的作用。首先将蚂蚁放置在配送中心0 处，依次进行下一个站点的选择。在进行下一个站点的选择时，要考虑路径上的信息素浓度τij(t)，它表示在t次迭代时，路径i到j上的信息素量，初始时刻均设置为0。当路径上经过的蚂蚁越多，留下的信息素量则越多，下一只蚂蚁则优先选择该路线，以此形成正反馈机制。另外，还要考虑距离的因素，当进行下一站点选择时，在满足其他条件的同时，优先选择距离较近的站点。设立启发函数ηij(t)=1/dij，表示随路径的加长，选择该站点的期望则越低。最后，考虑到本文中的是时间窗约束情况，加入时间紧迫因子，其中Ej表示时间窗的最早到达时间，Lj表示时间窗的最晚到达时间。同时考虑三种因素，参考文献［15-17］，设定第k只蚂蚁从i到j的转移概率函数如下：

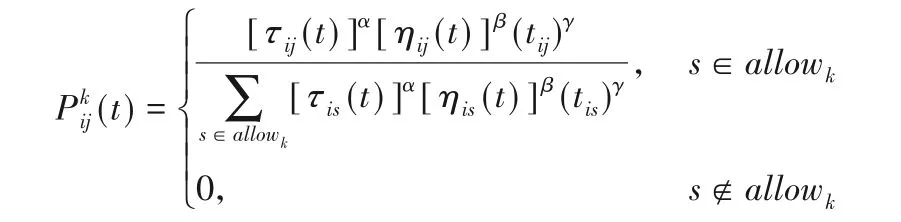
其中：allowk表示待访问站点的集合；α表示信息素的重要程度；β表示距离因子的重要程度；γ表示时间紧迫因子的重要程度。

3.2 信息素更新

每只蚂蚁在产生一条路径之后，在路径上释放信息素，原路径上的信息素随之逐渐消失。当所有蚂蚁完成一次循环后，各个客户点之间的信息素浓度需要随之更新。设定ρ为信息素的消逝程度，0 ＜ρ＜1，信息素更新的公式为：

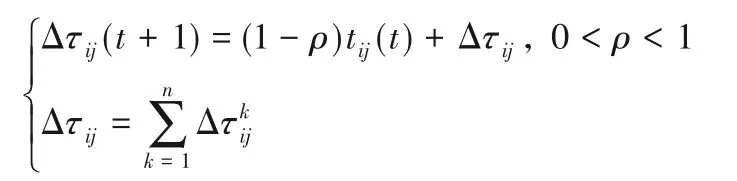
由公式可知，当路径距离越短时，该路径上各处的信息素浓度越高，下一只蚂蚁选择该路径的可能性越大。

3.3 算法步骤

步骤1 设置各代的蚂蚁数量和最大的迭代次数，初始化禁忌表，初始化各点之间的信息素浓度，初始化参数，计算各点之间的距离和车辆穿越两点之间的时间。

步骤2 把所有的蚂蚁都放置在配送中心0点处，禁忌表的第一列均设置为配送中心0处。

步骤3 依照禁忌表，根据残留的信息素量和启发式信息，受到转移概率函数的约束，独立选择下一位置。

步骤4 判断车辆电量到达下一站点时电量是否仍大于电池总量的15%，是则继续下一步；否则，前往最近的充电站进行充电，返回步骤3，重新选择下一站点。

步骤5 判断下一点的需求与已载货物之和是否超过车辆最大负载，若超过，在禁忌表上填入配送中心0 处，车辆返回配送中心装载货物，进行下一次配送任务的规划；否则填入选择的位置点。

步骤6 返回步骤3，直到单只蚂蚁把所有的客户点都加入到禁忌表中，再开始下一只蚂蚁的旅行。

步骤7 直到所有的蚂蚁都遍历了所有的客户点，找到所有可行解中的最优解，更新信息素，更新禁忌表，进行下一代的迭代，返回步骤1。

步骤8 迭代到最大次数，在各代中的最优解中挑选出一个最优的解。

4 算例分析

4.1 算例设置

本文以城市A 为例，采用Solomon 算例中的30 个客户的基本数据，按照现有的城市物流配送模式完成配送任务。各客户点的订单需求及服务时间如表2所示。

各个客户的位置坐标如图1 所示。图1 中：“0”表示配送中心的位置；“220 km，最大负载量为2 000 kg。按照我国现有的快速充电站”表示客户的位置坐标，共30个客户；“”表示充电站的位置，共10个充电站。由图1可知，客户均匀地分布在城市区域内，以配送中心为中心大致呈一个扇形。在表2中具体指出了各个客户的货物需求量以及服务时间窗，时间窗的范围为一个小时。为完成配送任务，需尽可能地在客户要求的服务时间内送达，且要保证车辆的路线距离更短，成本相对最低。在配送过程中，允许车辆当天多次配送，配送途中需要进行充电，车辆的充电时间需要考虑在内。

根据负载的不同，纯电动汽车的行驶里程为180 km～的特点，设定充电时间关于充电量的比率系数η为2，表示当充电量为1 kWh时，充电时间为2 min。该区域内设有10个充电站，编号为C1 到C10。车辆在配送中心的装货时间设定为30 min，在每一站点的停留卸货时间为10 min。

采用Matlab2016 编程语言对该案例进行求解，运行环境为64 位Windows 10 操作系统，运行内存为4 GB，CPU 频率为1.60 GHz。运行10次，选取最优的一次运行结果。

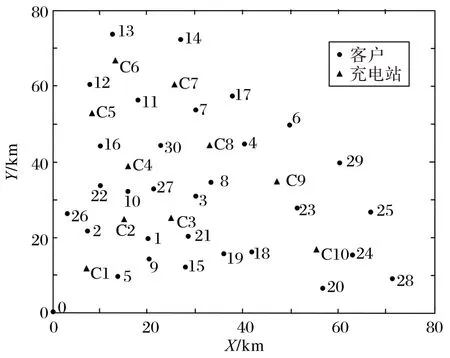
图1 客户位置坐标Fig.1 Customer location coordinates

4.2 结果及分析

4.2.1 路径规划及充电策略分析

蚁群算法是一种仿生学的智能算法，模拟蚂蚁的先天觅食行为，在求解路径规划问题时有着较好的优势。在模型求解中，转移概率函数中的相关参数对求解的结果及求解的速度有着较大的影响。其中，信息素的重要程度α过大时，蚂蚁随机选择路径的概率较小，过小时又会产生局部最优的结果。距离因子β过大或过小时，容易导致路径局部最优［13］；时间紧迫因子γ越小时，蚂蚁会自动选择更近的时间窗［15］。根据本文的模型特点，设置α=1，β=5，γ=2，结合4.1 节设置的案例，求解得到路径规划如图2所示。

各个车辆的路径、起始时间、充电次数及行驶里程如表3所示。

由图2和表3可知，该天的配送任务由三辆纯电动汽车完成，车辆1、2、3 的行驶里程分别为275.79 km、266.31 km、278.53 km。三辆车均在中途充电一次，车辆1 在C3 充电站充电，车辆2 在C6 充电站充电，车辆3 在C1 充电站充电。每辆车当天均执行两次配送任务，提高了车辆的利用率，减少对车辆的使用，同时也降低了配备的司机的人工成本。

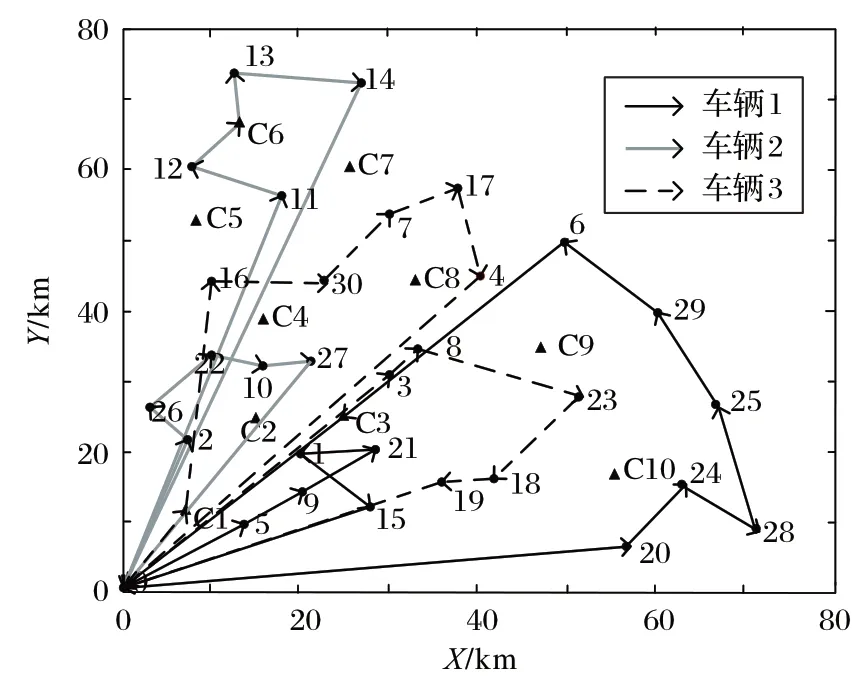
图2 路径规划Fig.2 Path planning

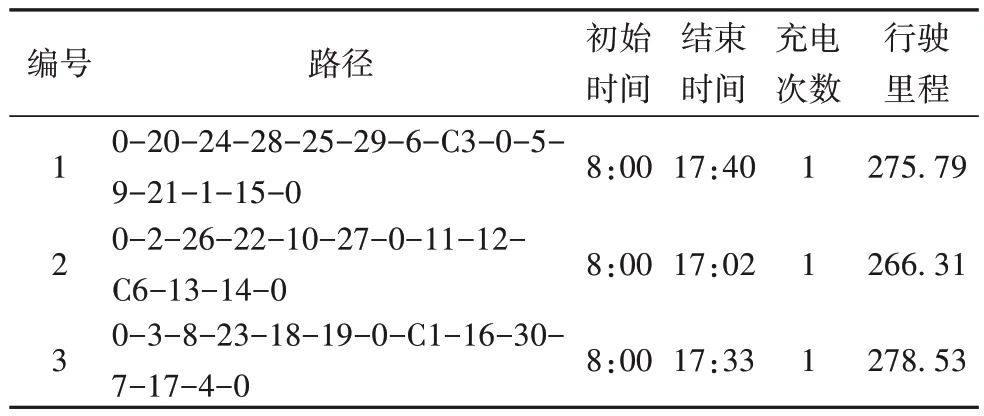
表3 各车辆行驶记录Tab.3 Driving records of vehicles

4.2.2 考虑负载对路径的影响分析

本文考虑了负载对车辆实时能耗的影响，通过建立功率关于负载重量的能耗函数，计算车辆的实时能耗情况，来为路径规划和充电策略提供依据。传统的能耗计算方法是设定一个稳定值，根据目前我国纯电动货车的实际参数，设定车辆在速度为50 km/h、匀速行驶的情况下，每小时的耗电功率为12.5 kW，结合本文的案例，对是否考虑负载情况下的路径规划及充电策略进行比较分析。表4 为两种情况下的参数比较。

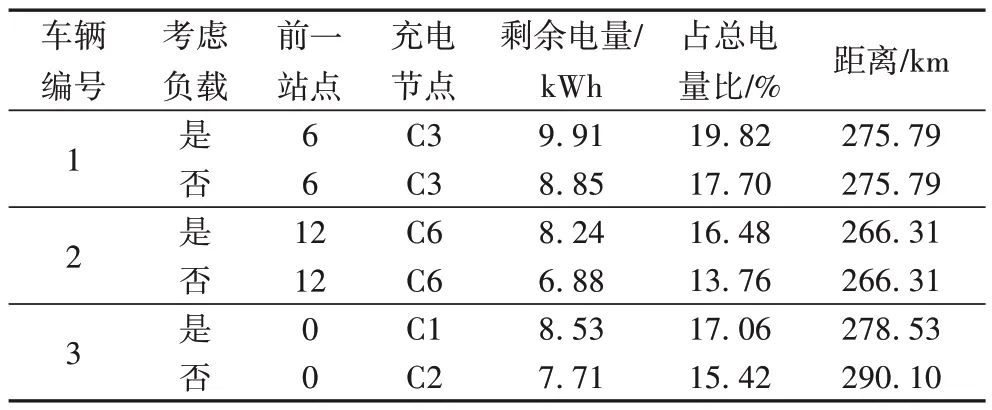
表4 是否考虑负载影响对比Tab.4 Comparison of considering or not considering load impact

由表4 可知，车辆1 和车辆2 在路径规划和充电站点的选择上没有区别，但车辆2在不考虑负载的影响下，完成客户12的配送任务之后，去最近的充电站C6 时，剩余电量只剩13.76%，这会导致车辆过度消耗电量，甚至可能引起剩余电量不足的后果。车辆3 在不考虑负载影响时，选择的是充电站C2，电量正常，但是总路径却增加了11.57 km。所以，考虑负载对能耗的实时影响，便于安排合适的充电计划，在路径规划上也能有所优化。

4.2.3 运营成本比较分析

该次配送情况下，各车辆成本结果如表5所示。

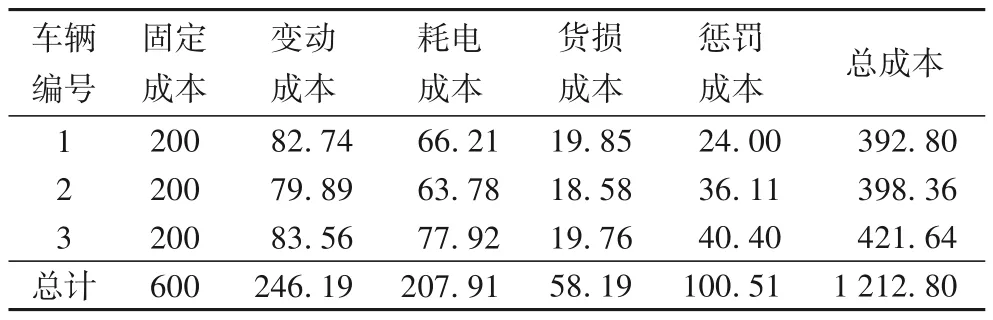
表5 各车辆各项成本统计 单位：元Tab.5 Cost statistics of vehicles unit：Yuan

表6 为电动车辆与燃油车辆在同种情况下的运营成本对比。

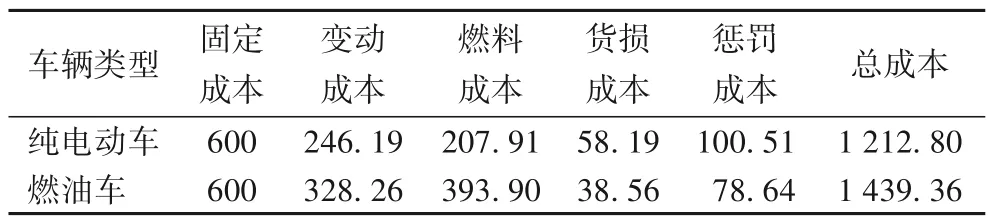
表6 不同车型成本比较 单位：元Tab.6 Cost comparison of different vehicle types unit：Yuan

由表6 可知，在不考虑纯电动车辆的购置成本情况下，纯电动车辆的运营成本比传统燃油车辆低。一方面是因为纯电动货车定期保养的成本较低，另一方面是因为燃油的成本比耗电的成本要高得多。目前用纯电动汽车进行物流配送不能普及的主要原因之一就是纯电动汽车的车辆购置成本和更换电池的费用较高。但是随着纯电动汽车和电池的成本的下降，纯电动汽车在城市物流配送中的应用，不仅可以节约成本，更能降低对城市的空气污染及噪声污染。另外，随着充电基础设施的大力建设，纯电动车辆在路径规划和充电策略上也能进一步优化。

4.3 不同规模算例分析

以上的算例包含30 个客户、10 个快速充电站，是一个较小的数据规模。随着数据规模的增加，为研究是否考虑负载情况对车辆路径规划及充电策略的影响，再选取不同规模的样本数据进行分析。以C表示客户数量，R表示充电站的数量。每组实验进行10 次，选取最优的一个结果，对比情况如表7所示。

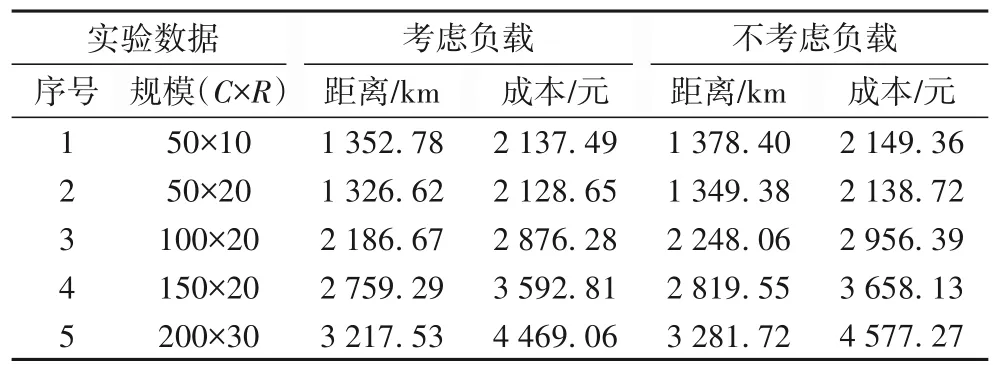
表7 不同规模算例比较分析Tab.7 Comparative analysis of different scale examples

由表7 可知，在考虑负载情况下，车辆的当天总行驶距离要比不考虑负载时更优，配送路径平均减少2%。另外，配送成本也相对有所降低，从而验证了考虑负载影响对配送路径规划优化作用。另一方面，在实验中，不考虑负载对实时影响时，车辆实际电量存在低于总电量15%的情况，这对配送任务的完成会有一定的干扰。

4.4 算法比较

本文研究的问题属于路径规划问题的范畴，解决此类问题较多采用遗传算法（GA）。而在文中，设计了蚁群（ACO）算法进行求解。蚁群算法在处理路径规划问题时，采用正反馈机制，能高效地寻找最优结果。针对4.3节中实验的5组样本数据，采用GA 和ACO 算法进行实验对比，每组数据均实验10次，采取最优的一次结果。遗传算法的种群规模为100，最大迭代次数为500，交叉概率为0.8，变异概率为0.2。结果对比如表8所示。

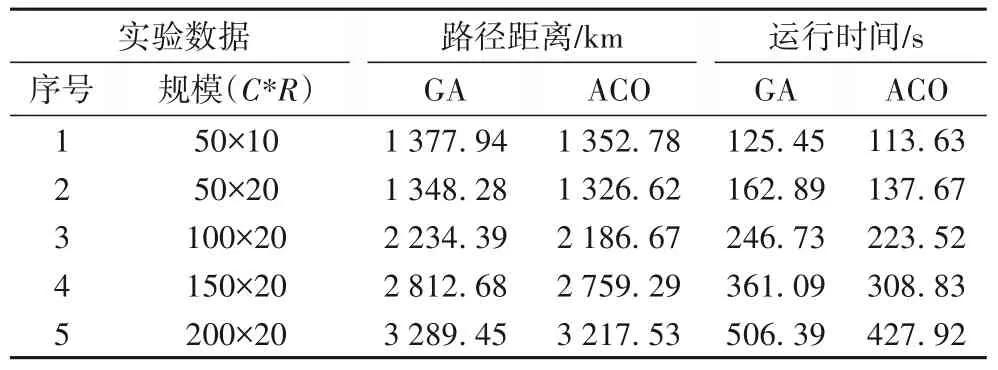
表8 GA与ACO实验结果对比Tab.8 Comparison of experimental results of GA and ACO

由实验结果对比可知，对于5组样本数据，ACO 在求解这一问题时，能够得到一个更优的结果；在运行时间上，ACO 比GA也是有着更快的求解速度。由此可知，蚁群算法在求解这一问题时具有较好的特性。

5 结语

本文考虑新能源汽车的发展趋势，建立了以纯电动汽车为基础的城市物流配送模型，优化配送路径，降低企业的物流配送成本。由于纯电动汽车在一整天的配送过程中需要进行充电，并且充电时间较长不可忽略，故本文结合客户的时间窗约束以及负载对车辆实时耗电的影响，合理制定电动汽车的充电计划，避免超出客户的服务时间，提高服务的时效性。目前，由于纯电动汽车的购买成本较高，电池的技术尚未成熟，相较于燃油车来说，在固定成本这一环节仍存在一定的劣势。但随着环保力度的加大以及电池技术的进步，用纯电动汽车来进行城市物流的配送将会得到普及。