林果业修剪机械手的设计与试验

潘志勇,闫 岩

(1.长春理工大学,长春 130000;2.长春大学,长春 130022)

0 引言

在以往林果业修剪工作中,通常采用由绿化工作人员,通过手持油锯或是刀具修剪树枝的方式,实现对林果业树木的修理和修剪,但其工作效率低且质量差。随着科学技术的发展,已经有专门针对林果业树木修剪的机器,常见的有林业修剪机器人和车载式绿篱修剪机[1]。林业修剪机器人在应用中,修剪具有竖直性,其功能相对单一。此外,有学者在研究中,针对林果业树木开发了车载式绿篱修剪机[2]。此种修剪机具有竖直修剪性和水平性,对于日后丰富林果业修剪机械手的研究,奠定了坚实的基础。自进入信息化时代后,林果业修剪机械的设计水平日益提升,林果业修剪机械手产品日益呈现出人性化、环保化、自动化与智能化趋势。为此,本文展开对林果业修剪机械手的设计与试验。

1 总体设计

通常情况下,总体设计可以分为总体构思及基本方案。在总体构思中,要明确修剪机械手的类型,并对不同的类型进行合理选择[4]。由于林果业的树木尺寸相对较大,所以在采用修剪机械手对其进行修剪时,需要遵循工业机械手应用的基本原则,也要注意林果业修剪的特殊性。一般来说,林果业修剪机械手可以分为4类。①直角坐标型机械手;②极坐标型机械手;③圆柱坐标型机械手;④关节坐标型机械手。在直角坐标型机械手中,主要涵盖了3个运动方向,3个方向是相互垂直、可移动的关节,优势体现为控制操作方法简单、精度较高;缺陷体现为占地面积大且工作空间小。在极坐标型机械手中,主要涵盖了两个旋转关节和一个移动关节,优势体现为灵活性较高、能够在较大的空间范围内活动;缺陷体现为无论是精度还是刚度均相对较弱。在圆柱坐标型机械手中,主要涵盖了两个移动关节和一个旋转关节,应用优势体现为控制操作方法相对简单快捷,且占用的活动空间较小[5];缺陷较少。在关节坐标型机械手中,主要涵盖了3个旋转关节,应用优势体现为能够活动的空间范围较大,且灵活度较高;缺陷体现为对机械手控制系统的实时性要求相对较高,精度性相对不足。

为了能够使修剪机械手的设计符合林果业的修剪要求,需要林果业修剪机械手具有较好的修剪适应能力。在此基础上,林果业修剪机械手的具体要求可以概括为以下几点:一是规避障碍。林果业中的树木形态较高,苗木中央也可能设置电线杆或是路牌,且修剪机械手需要深入到绿化带中进行作业,应能够规避障碍。二是活动范围大。林业或是果业种植范围较广,修剪作业内容多、范围广。在此情况下,修剪机械手要能够在较为广泛的空间内实现对树木的修剪,机械手活动范围要大。三是要有过载保护措施[6]。

针对本研究中选择的林果业,采用具有直角坐标和关节坐标为一体的六自由度的绿篱苗木修剪机械手。林果业修剪机械人员在操作前,要深入分析修剪机械手的主要结构,明确各结构的构成,对应用此种修剪机械手的结构和关节串联结构的选择原因进行综合性分析。在此基础上,探讨林果业修剪机械手的运动特性,主要以修剪机械手的坐标的建立步骤加以阐述,明确如何有效地构建合理修剪机械手坐标系。同时,探讨林果业修剪机械手运动的正解和逆解情况,根据相应的参数计算,针对林果业修剪机械手设计仿真轨迹求取方法和仿真效果,展开综合的叙述。

2 主要结构及运动学分析

2.1 林果业修剪机械手的主要结构

通常情况下,修剪机械手采用的结构为关节串联式空间开链型结构[7]。分析应用此种结构的原因,主要是在修剪绿篱苗木过程中,修剪机械手需要自由、任意带动刀具进行旋转运动,使其能够在比较充足的空间范围内活动。林果业修剪机械手的空间开链结构共有6个连杆和6个转动关节,包括旋转机构、大臂、中臂、小臂和转盘,如图1所示。在小臂前端,安装了修剪的刀具。在修剪苗木时,通过对大臂、中臂和小臂的调节,实现对苗木长短和形状的修剪。该苗木修剪机械手的关节,均属于转动关节,能够通过旋转的方式,实现对苗木的自由修剪。转动关节包括有肩关节、腰关节、小臂转动关节、腕部回转关节和肘关节等。

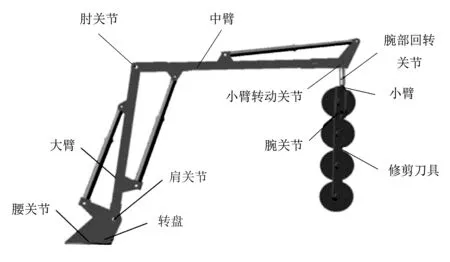
图1 绿篱苗木修剪机械手三维实体模型示意图

2.2 林果业修剪机械手运动学分析

图2为绿篱苗木修剪机械手结构简易示意图。根据图2能够进行机械手的基本构成部分和各关节的分析,比较全面地对修剪机械手的具体结构展开综合研究。

在建立苗木修剪机械手的坐标时,主要采用的是D-H参数法,对修剪机械手运动学方程进行建立[8]。在所建立的坐标中,第0连杆,作为坐标的旋转底盘。通常来说,大臂会与旋转底盘进行连接,而与旋转底盘最先连接的大臂,将其看作为第1连杆;根据此种类推方式,将最后一个与旋转底盘连接的大臂,作为第5连杆,且将该连杆与腕关节相连,也将其称之为修剪刀头。按照D-H参数法所建立的坐标系,将绿篱苗木修剪机械手的各杆件坐标系,建立到该坐标轴上,如图3所示。

图2 绿篱苗木修剪机械手结构简易示意图

图3 绿篱苗木修剪机械手各连杆坐标系示意图

根据图3所展示的信息能够了解到:ai-1为在Xi-1轴方向上两个轴之间的距离,分别是Zi-1轴到Zi轴之间距离;αi-1为旋转角度,主要代表两个轴围着Xi-1轴旋转的角度,分别是Zi-1轴到Zi轴的围绕角度。di-1为在Zi-1轴方向上两个轴之间的距离,分别是Xi-1轴到Xi轴之间距离;θi为旋转角度,主要代表两个轴围着这Zi轴旋转的角度,分别是Xi-1轴到Xi轴的围绕角度[9]。

根据D-H参数法所建立的坐标系,进一步对绿篱苗木修剪机械手各个连杆的D-H参数和关节变量进行综合确定,如表1所示。由表1可知:当关节为1时,连杆夹角为θ1,扭转角为π/2,杆长为α1,偏置和cosα值均为0,此时sinθ值为1;当关节为2时,连杆夹角为θ2,扭转角为0,杆长为α2,偏置sinα值为0,此时cosα值为1;当关节为6时,连杆夹角为θ6,扭转角、杆长、偏置、sinα值均为0,cosα值为1。

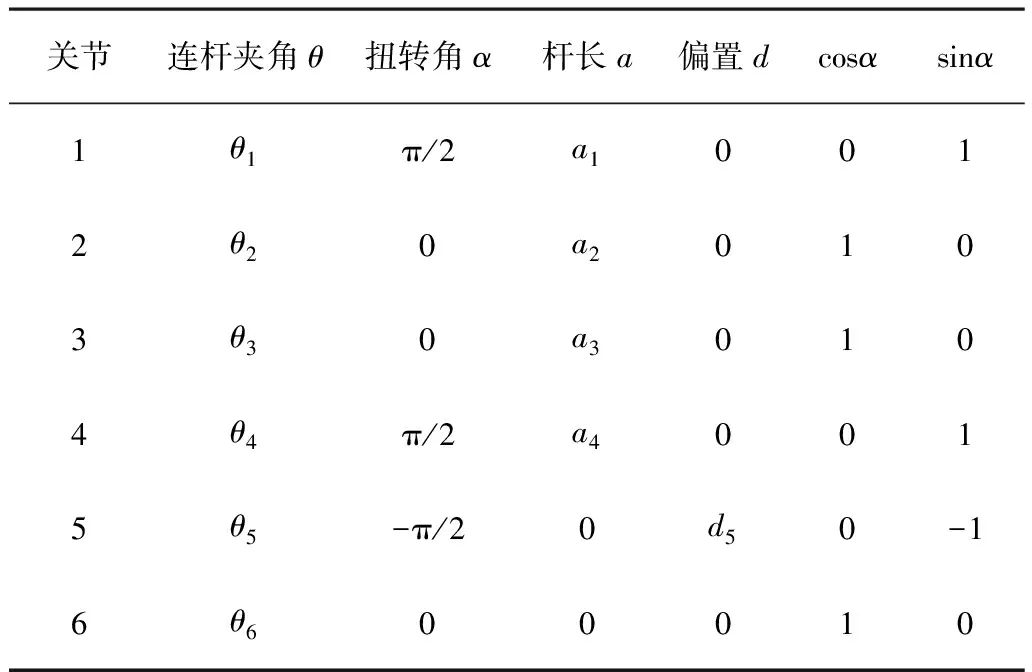
表1 绿篱苗木修剪机械手的D-H参数表

在林果业修剪机械手运动学中,通常将运动学分为正解和逆解[10]。运动学正解,主要是在已知的条件下,求解苗木修剪机械手末端执行器的位置和姿态。一般来说,在建立起连杆的坐标系,确定各个连杆的结构参数以后,可以通过式(1),完成对苗木修剪机械手各个连杆之间的位置、姿态的变换,即

(1)

其中,ci=cosθi,si=sinθi,cαi=cosαi,sα=sinαi。根据该公式,对苗木修剪机械手的正解进行假设,设cij=cos(θi+θj),sij=sin(θi+θj),cijk=cos(θi+θj+θk),sijk=sin(θi+θj+θk)。在此基础上,将表1中所示的D-H各项参数,分别代入到式(1)中,则能够求得苗木修剪机械手相邻各连杆之间的位置、姿态矩阵,即

根据上述6个公式,将各个相邻的连杆变换矩阵相乘,彼此相乘后能够得到苗木修剪机械手末端的位置、姿态矩阵公式,即

(2)

运动学逆解[11],主要是指掌握苗木修剪机械手的综合信息下,以修剪机械手各个连杆参数为主,针对苗木修剪机械手的末端执行器,确定苗木修剪机械刀具相对应参考坐标系的位置与姿态。因此,反过来求解得出使苗木修剪机械刀具达到预期修剪目的和要求的修剪机械手各个关节变量情况。通常来说,可以采用反变换方法,对苗木修剪机械手的变量采用逆运动方程完成求解。换句话而言,就是采用位置矩阵的逆变换方法,依次的左乘式(2)方程,并使两边对应元素相等。

逆解的方程为

(3)

根据林果业修剪机械手运动学的逆解求取方法,为了使式(3)中等号左右两侧的元素相等,能够得出以下公式:θ1=αtan2(Py,Px)。根据该公式,能够求出θ1在特定区间[-180°,180°]内的解,由此了解林果业修剪机械手运动学的具体逆解方法。

同理,根据上述公式的计算方式,可以进一步实现对其余关节变量的计算。具体计算方式为

在上述公式的基础上,能够有效求得苗木修剪机械手关节变量相对应的关节转角,具体计算方式为

θ4=αtan2(Pzs23-α2c3-α1c23-α3+Pys1c23+c1Pxc23,

-α1s3-α1c23+Pys1s23+c1Pxs23)

θ5=αtan2[nxs1-nyc1,-c6(αxs1-αyc1)]

θ6=αtan2(-oxs1+oyc1,nxs1-nyc1)

通过对上述公式的分析,可以进一步计算得出A、B、C、D、E的结果,其结果为

A=Pxc1-α1+Pys1-d5αz/s5

B=Pz+d5(αxc1+αys1)/s5

C=2×(A2+B2+α22-α32)/α2

D=Pzs2-α1c2-α2+Pxc1c2+Pys1c2+Pzc2+α1s2-

Pxc1s2-Pys1s2;E=d5(αzs2+αxc1c2+αys1c2-αzc2+αxc1s2+αys1s2)/s5

3 林果业修剪机械手设计仿真效果

3.1 林果业修剪机械手设计仿真轨迹的求取分析

图4为修剪机械手圆球螺旋轨迹分析示意图。根据图4信息能够看出,圆球表面上的点主要以中心轴为主,做螺旋旋转运动。

图4 修剪机械手圆球螺旋轨迹分析示意图

在运动过程中,圆球的轨迹表现为圆球螺旋线[12-13]。苗木修剪机械手在对绿篱树木作圆球造型时,通常是以修剪机械手的末端作为主要的运动点,围绕中心点的竖直旋转中线, 做圆球螺旋运动, 从而达到圆球造型修剪目的。图4中,环形树木的母线表现为圆弧线,苗木修剪刀盘中心的法线与旋转轴线之间的夹角主要用η表示,与之对应的弧角用φ表示,苗木修剪刀盘修剪时围绕旋转轴转过的角度用λ表示。

所以,φ数值一般会在π/2～2π/3之间。在设置坐标系相关坐标值时,通常将圆球顶相对应的坐标值设置为x0、y0、z0,具体的坐标数值是根据修剪机械手的初始位置和姿态进行确定的。其中,x、y、z是苗木修剪机械手末端的坐标值。在此基础上,在对苗木做圆球造型时,具体的公式为

z0-z=R-Rcosη

(4)

为了使修剪的树木保持圆球形态,在树枝不会露切的前提下,修剪机械手的圆球螺旋需要满足公式(5)的条件,即

λ/η=2Nπ/φ

(5)

其中,N为在树木修剪期间,树枝恰好不会发生露切的现象。当η逐渐增加到φ时,苗木修剪机械刀盘将围绕旋转轴转动的圈数为

N=φ/[2αrcsin(d/2R)]

(6)

其中,d所代表的含义是苗木修剪机械手刀盘的直径,R所代表的含义是所修剪的绿篱树木的半径。在此基础上,将式(5)和式(6)相结合,则有

λ=πη/αrcsin(d/2R)

(7)

此外,根据图4,也能够明确苗木修剪机械手的坐标,具体的坐标公式为

(8)

根据式(8),将z作为自变量时,可以结合式(4)、式(7)和式(8),进一步实现对苗木圆球造型时以序列轨迹位置、姿势的求取。同时,将其代入到逆解方程中后,能够快速实现对苗木修剪机械手各个关节变量转角的求取。设置:α1为140mm,α2和α3为1 400mm,α4为0mm,d5为450mm。在此数据设置下,将机械手刀盘的直径d设置为200mm,圆球半径R设置为500mm,且取增量Δz为-1,求取600组数据。由于设置和要求取的点数较多,在此每间隔100组的基础上抽取一组数据进行计算。通过计算所得的苗木修剪机械手末端坐标数据、各关节变量转角数据,如表2所示。

表2 苗木检修机械手末端数据及各关节变量转角数据分析

3.2 林果业修剪机械手运动学的逆解仿真效果

在对林果业修剪机械手运动学逆解仿真效果进行分析时,对修剪机械手仿真过程进行综合的了解与分析,是尤为必要的[14-15]。从某种角度而言,苗木修剪机械手的结构相对复杂,以往常用的ADAMS实体建模功能,存在一定的薄弱现象。因此,在林果业修剪机械手运动学中,Pro/E三维模型逐渐被广泛应用于林果业修剪机械手中。本文中,由于阐述的内容主要以苗木修剪机械手的运动为主,所以在装配过程中,会将与机械手运动结果无关的相关配件删除,保留下来的,包括大臂、中臂、小臂、旋转机构、转盘和修建刀具。图5为苗木修剪机械手的仿真过程示意图,根据该图中信息,能够明确修剪机械手运动学逆解仿真的具体步骤。在Pro/E三维模型与ADAMS的辅助下,利用MECHANISM/Pro接口软件,设置Pro/E环境,对苗木修剪机械手各个关节进行定义,包括肩关节、肘关节和腰关节等。在此基础上,将模型导入到ADAMS中,在苗木修剪机械手各个关节部位分别建立不同的旋转驱动。根据模型,所建立的旋转驱动分别为Motion1-6。

图5 苗木修剪机械手的仿真过程示意图

将通过计算求得的θ1～6相关数据,导入到ADAMS模型中,由该模型生成与之相对应的6条SPLINE曲线;将所形成的曲线分别设置为SPLINE1-6,并对6个关节的SPLINE曲线进行调节与定义。通常情况下,用来调节和定义的工具为AKISPL,如在对苗木修剪机械手的腰关节驱动函数Motion1进行定义时,定义为AKISPL(time,0,SPLINE1,0);与此同时,运行仿真模型,对苗木修剪机械手的动力学进行求解。在模型运行后,可以采用“Review”和“Create Ttace Spline”命令,完成对苗木修剪机械手末端相对地面轨迹曲线的综合建立。图6为侧向投影仪示意图,图7为竖直方向投影仪示意图。根据图6和图7相关信息,能够从比较全面的角度上掌握圆球螺旋的轨迹。根据观察发现曲线具有光滑性和整齐性,从侧向和竖直方向的投影观察,轨迹的包络线均呈现出圆形态,由此可证明在苗木修剪机械手运行中螺旋轨迹的正确性。

图6 侧向投影仪示意图

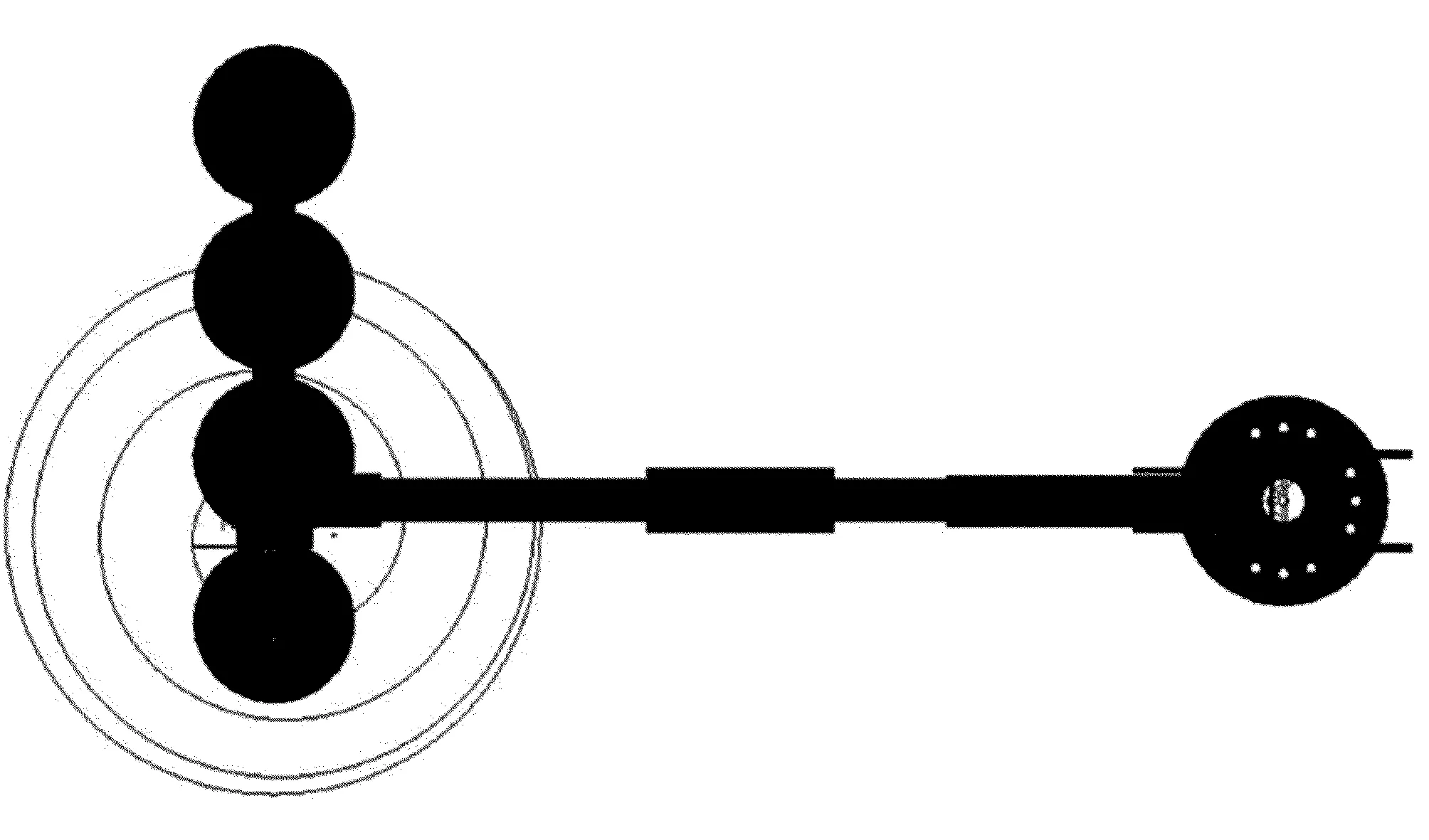
图7 竖直方向投影仪示意图

图8为修剪机械手Marker点在三方向位移的变化曲线示意图。由图8可知:在0、10、20、30s等时刻,可得出了x、y和z的数值,标注的总时间为60s,间隔为10s。根据对不同时刻不同方向数据的分析,发现x从小到大依次为:0、-245.0、-129.8、331.3、-397.2、405.4、-397.2;y从小到大依次的数值为:1 540.0、1 366.8、1 918.3、1 223.4、1 826.7、1 247.3、1 826.7;z从小到大依次的数值为950、850、750、650、550、450、350。根据3个不同方向的数值,结合表2中圆球轨迹的x、y、z3组理论值,发现该数值与表2中相关数据重合,由此证明所建立的运动学方程正解与逆解的正确性。

图8 修剪机械手Marker点在三方向位移的变化曲线示意图

在明确苗木修剪机械手运动学方程及其相关数据的前提下,对机械手各个关节的角加速度曲线展开了综合性的分析与探讨。图9为苗木修剪机械手各关节角加速度曲线示意图。在分析机械手各关节角加速度曲线示意图时,主要分析的是肩关节、腰关节、小臂转动关节、肘关节及腕部回转关节及腕关节6个关节。其中,肩关节的最大角加速度为7.2、3.8、6.7、2.3、10.4、3.7(°)/s2。由图9可知:修剪机械手角加速度的曲线,表现为平缓光滑,且数值相对较小;机械手运动相对平稳,效果较好。

图9 修剪机械手角加速度曲线示意图

经研究证实:光滑和平缓曲线的关节包括肩关节、腰关节、小臂转动关节、肘关节、腕部回转关节及腕关节6个关节[16-17],各个关节在不同60s内的不同时间段内,其角加速度数值变化较小,证实了苗木修剪机械手在造型修剪期间,能够实现对圆球造型的平稳修剪。将图8中的仿真数据与表2中的圆球轨迹x、y、z3方向理论数值进行对比分析发现:图和表中的相关数据重合,能够充分证明修剪机械手运动学解的正确性和准确性;也从设计的角度上,证实了借助D-H理论对林果业修剪机械化手六自由度运动学解是可行性的。通过分析发现,与其他相关理论和方法相比较,D-H的模型理论方法在林果业修剪机械手中的应用,具有突出性的优势:①D-H的操作方法相对便捷[18-19]。在应用该理论方法时,操作人员按照相应的操作流程和标准,即可完成设计和研究。②D-H的计算准确性较高。该理论方法在应用中,能够从科学的角度上,对数值进行求取,从而提高计算结果的准确性。③D-H方法下,所求取的运动学逆解,能够更加方便地实现对林果业修剪机械手的实时控制。借助运动学逆解,能够快速掌握修剪机械手的正解情况、计算步骤等,并通过反运算的方式实现对机械手的控制[20]。此外,在D-H方法的基础上,对Pro/E和ADAMS模型进行联合,结果发现:Pro/E和ADAMS模型联合仿真技术的应用,具有简单便捷、直观性强的优势,在林果业修剪机械手运动学仿真校验中,具有突出价值。

3.3 试验及结果

3.3.1 试验流程

具体的试验流程为:①对本次试验的基本原理、试验方案、试验装置及相关参数进行简介;②对试验中选择的机械手、拖拉机加以介绍;③阐述试验过程,说明试验的具体操作步骤;④根据试验所得相关信息,归纳和总结试验结果,并附加本次试验用到的相关表格和图示。

3.3.2 试验准备及实施

在林果业修剪机械手试验前,要对各关节进行检修,确保各环节的运行。在关节点运行试验中,对修剪机械手的旋转机构、大臂、中臂、小臂和转盘、肩关节、腰关节、小臂转动关节、腕部回转关节和肘关节等,进行调整,使旋转机构能够完成360°的旋转。图10为雷沃M254-E型号的拖拉机示意图,已将修剪机械手安装到该拖拉机上。

图10 雷沃M254-E型号的拖拉机示意图

经过试验中对修剪机械手样机活动的空间范围测量,具体参数如表3所示。

表3 林果业木苗修剪机械手样机活动的空间范围

3.3.3 试验过程与结果分析

在圆球修剪试验中,将修剪机械手的承载车移至需要修剪的绿篱旁,将刀具正对树木中心的上方,设置参数:连杆夹角(θ)为θ1,扭转角(α)为π/2,杆长(α)为α1,偏置(d)为0,cos(α)为0,sin(α)为1;设定机械手刀盘的直径d为200mm,圆球半径R为500mm;旋转机械手,能够得到x、y、z的相关数据,通过数据的分析证实在该设计下,树木圆球修剪相对平整。在平面修剪过程中,匀速的移动修建刀盘,分别在0、10、20、30、40、50、60s的时刻,对不同方向的数据进行分析,结果表明:X在0s时刻的数值是0,在60s时刻的数值是-397.2;y在0s时刻的数值是1 540.0,在60s时刻的数值是1 826.7;z在0s时刻的数值是950,在60s时刻的数值是350。试验结果表明:依据设计的相应数据能够实现对圆球的修剪,且在实际修剪中可以加快修剪速度。

4 结论

针对当前林果业修剪机械手的应用情况,重点阐述了林果业修剪机械手的设计,提出了绿篱苗木修剪机械手,该机械手具有六自由度的优势。同时,采用D-H理论,对修剪机械手运动学的模型参数进行了分析,结合相应的模型参数和理论,对修剪机械手运动学的正解和逆解进行了分析和推导。在此基础上,将Pro/E和ADAMS两种模型加以联合,通过对模型的联合性应用,形成联合仿真技术,实现对修剪机械手运动学三维建模及圆球造型的仿真。通过仿真测量的方式,对测量数据结果进行整理、归纳和分析,从直接角度上证实了修剪机械手运动学模型的正确性和数据的准确性。该修剪机械手各关节加速度曲线的平缓、数值变化幅度小,间接性证实了修剪机械手在工作中的运行相对平稳。