飞行载具扇叶驱动展开机构的扭矩与气动仿真研究

刘 杰， 卞新宇， 倪寿勇, 王志鹏

(1.南京工业职业技术大学 机械工程学院， 江苏 南京 210023；2.桂林电子科技大学 机电工程学院, 广西 桂林 541004)

引言

针对投送小尺寸紧急物品的任务，已具有多种比较成熟的现代化途径，例如各种航空器托运、无人机飞行器运送、地面输送以及抛射推进等方式[1-5]，但运送成本和时效性难以兼得。目前空中投送尚存在航程限制、投送距离限制以及投送落点精度偏差较大等不足，而且，常用降落投物伞使得载具降落速度慢，目标明显且易受到横向风场影响，从而导致实际降落点偏离预定位置距离较大，同时，减速装置一般为柔性重量轻、弹性好材料所制，易受高建筑物、线网绳索、野外树枝等突兀位置钩挂。

因此，为较好克服上述载具部分缺点[6-9]，本研究设计了一种被动式小尺寸扇叶驱动变连杆展开机构的载具，结构如图1a所示，由被动式扇叶驱动、联轴器、扭矩倍增器、连杆和承载叶片以及具有防止回转作用的棘轮机构组成；图1b为载具完全展开的飞行姿态，其张开过程可通过如下传动链完成：接收到指令风帽自动脱落，空气来流推动扇叶旋转，通过联轴器以及减速层的扭矩倍增器将扇叶产生的扭矩放大并传递到丝杠，丝杠两端进行全向固定支承，将旋转运动转化为丝杠螺母移动，然后推动连杆将承载叶片展开，即可完成由图1a所示状态至图1b所示状态的转变。

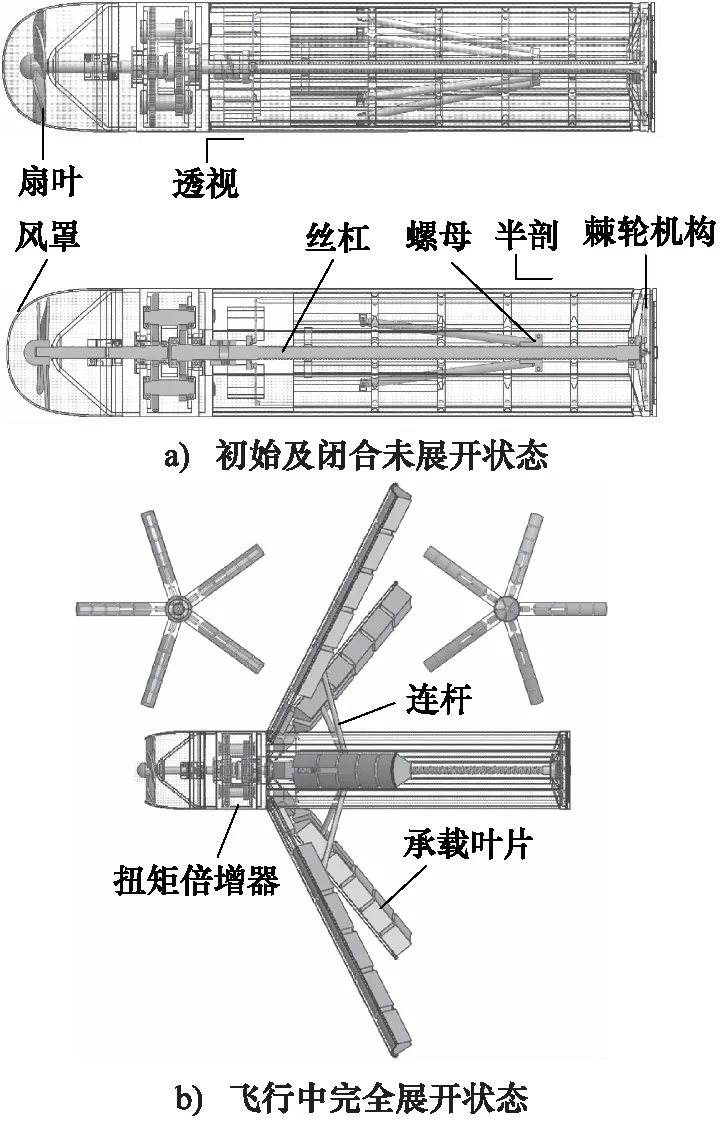
图1 载具机构

对于可展开机构的驱动问题，一直是航天与气动等方面研究热点，有研究开展了驱动分布式桁架天线展开的方法研究和数值模拟[10]，对可展开机构连杆存在的加工误差进行了研究分析，来降低多环闭链可展机构的装配和加工难度[11-12]，还有提到构建多环耦合的伞状可展机构和一种仅含转动副的直线可展单元并求解得到机构所需的驱动力矩[13-14]，针对大范围运动与大变形耦合等复杂动力学问题。

本研究针对丝杠螺母直线驱动与连杆可展开机构合并串联，连杆不存在大变形，利用小尺寸气动扇叶产生扭矩传递至驱动机构并带动连杆机构展开， 展开过程仅利用被动式扇叶接收风能提供的驱动力矩，需克服扇叶风阻、载荷重力以及滑动摩擦阻力等[15-17]。为此，研究内容中计算了风能提供的扭矩数值及气动仿真扇叶风阻，给出并校核丝杠转速、来流速度及丝杠扭矩之间的关联，可为后续开展载具的连杆长度、扇叶强度、空间载荷分布以及不同来流风速下风阻计算提供一定的理论参考。

1 扇叶扭矩计算推导

将具有一定速度的载具扇叶扭矩计算，转变为利用风能驱动叶片旋转模型[18-20]，采用叶素理论，将每个叶片分割成N等份，即叶素，如图2a所示，保证叶素在叶片上的位置不同而形状不变。由于每个叶素的旋转速度、弦长和结构扭角不同，因此叶片在径向各处的气动特性存在差异，需得到各个叶素的气动特征，然后沿径向进行积分，才可得到整个叶片的对应值。

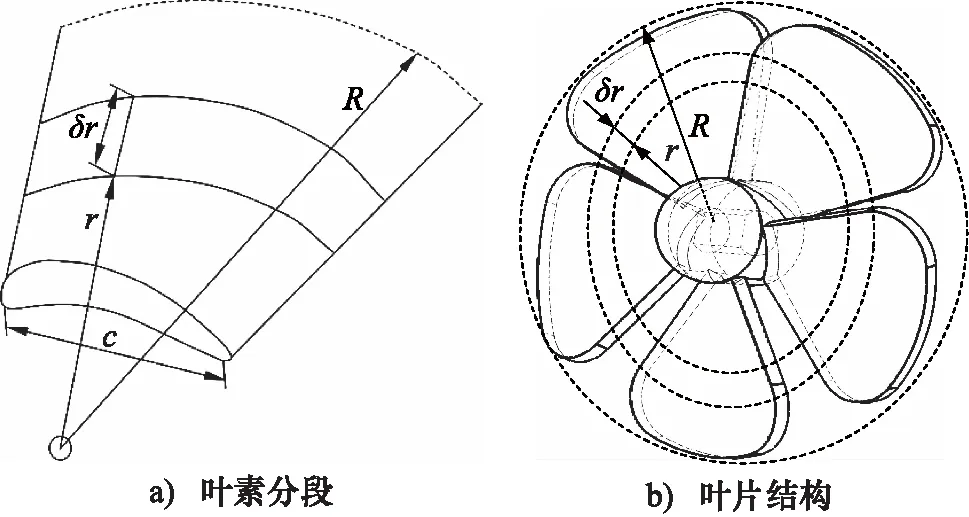
图2 扇叶结构示意图

所采用的扇叶结构如图2所示，其中扇叶半径为R，弦长为c，扇叶中心到任意截面的半径为r。定义扇叶旋转角速度为ω，来流风速为v，计算叶素上的速度组成关系，分析各个叶素所受到的力和力矩。由于载具在闭合发射时为弹体形状，扇叶径向尺寸被限制在发射机构的管径范围内，为利用小迎风面提供足够的驱动扭矩，故将扇叶数目B选定为5片，可具有高效率、低噪声以及较高的最大风能利用系数，该扭矩需要克服传动链摩擦力、叶片展开风阻以及重力矩的作用。下面利用叶素理论进行分析计算。

如图3所示，设定一个叶片数B=5的扇叶，半径为R，旋转速度为ω，来流风速为v，根据图4中的速度矢量，则距离转轴r处的叶素轴向风速为：

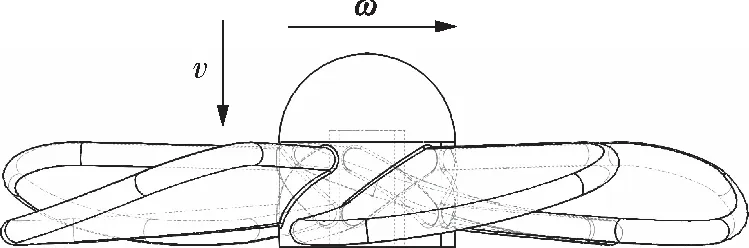
图3 旋转速度及来流风向

vaxi=v(1-a)

(1)

则此叶素的线速度，即平行于风轮旋转平面的切向气流速度分量：

vrot=ωr(1+a′)

(2)

半径r处的叶素相对合速度为：

(3)

式中，a——轴向诱导因子

a′——切向诱导因子

攻角α为入流角φ与叶素结构扭角β之差:

α=φ-β

(4)

式中，β——叶片弦线与扇叶旋转平面的夹角，即叶素的结构扭角

φ——入流角，即叶素相对速度与扇叶旋转平面之间的夹角

由结构测量得到攻角和入流角，根据攻角α查表[13]得到叶素叶片的升阻力系数Cl和Cd，部分已知参数如表1所示。

表1 已知参数

其入流角计算公式如下:

(5)

叶片升力垂直于合成速度W，阻力平行于合成速度W，根据已知的升力系数Cl和阻力系数Cd，如图4所示，则叶素单位长度的上升力L和阻力D，其升力L的计算公式为:

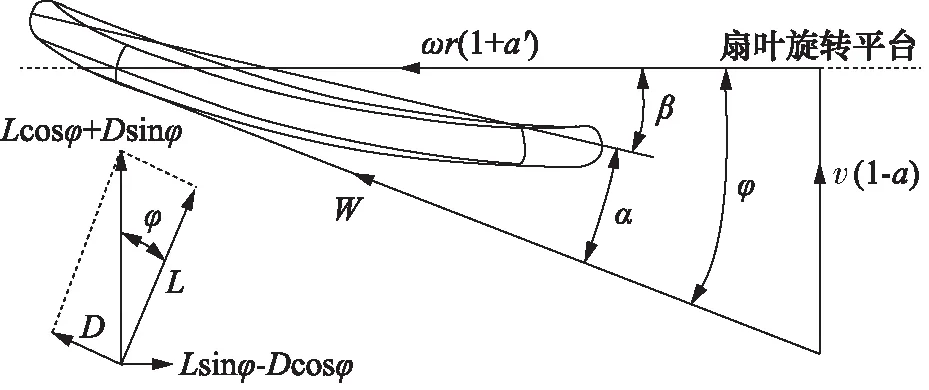
图4 半径r处叶素叶片平面内速度分量

(6)

阻力D计算公式为:

(7)

当扇叶在旋转状态下时，叶素气动力只考虑与扇叶旋转平面上的牵引力pt和扇叶旋转面上的推力pn，所以升力和阻力在这2个方向的投影为:

(8)

(9)

根据动量-叶素理论(BEM)假设作用于叶素上的力仅与通过叶素扫描的圆环中的气体动量有关。则在半径为r的扇叶上的法向推力和扭矩为:

dT=Bpndr

(10)

dM=rBptdr

(11)

对式(8)和式(9)进行转换，可得切向系数与法向力系数：

(12)

(13)

再根据图4中各个速度分量之间的关系，可以得出：

Wsinφ=v(1-a)

(14)

Wcosφ=ωr(1+a′)

(15)

将式(13)与式(14)代入式(10)可得：

(16)

将式(12)与(15)代入式(11)可得：

(17)

弦长实度σr为给定半径下的总叶片弦长与此半径上的周长之比，即:

(18)

在理想动量理论中轴向推力的微分型式方程为:

dT=4πρv2a(1-a)rdr

(19)

由式(16)和式(19)相等，则可以推算出轴向诱导因子a为:

(20)

在理想动量理论中推力转矩的微分型式方程为:

dM=4πρvωa′(1-a)r3dr

(21)

由式(17)和式(21)相等，推算出周向诱导因子a′为:

(22)

利用上述推导公式可以得到针对扇叶所产生的扭矩数值。在已知来流密度1.17 kg/m3、扇叶半径R为40 mm以及表1中的条件下。根据上述理想动量中的推理转矩的微分方程(17)可得出扇叶的扭矩和丝杠转速之间的关系，如图5所示，为快速的非线性增长，当来流风速v为100 m/s，随着丝杠转速ωc的增加，丝杠扭矩Tc相应增加。

图5 来流风速下的扭矩随转速之间的关系

2 载具完全展开的气动仿真

上述通过叶素理论，计算了一定来流风速下的丝杠所获得的扭矩，下面通过采用Flow Simulation专业流体模块进行建模[18]，计算完全展开机构的流体状况及扇叶与丝杠平衡时的扭矩，进行理论和仿真计算的相互验证与对比。Flow Simulation通过迭代求解非稳态Navies-Stokes方程来计算结果，首先设置收敛目标，可用来控制流体计算时的收敛性情况，并可在计算完成后提取相应的数据。

此次流体分析中，流体介质为常温情况下的空气，其密度取1.17 kg/m3，环境条件为温度298.15 K，大气压约为0.1 MPa，边界条件定义来流风速v为100 m/s，同时确定重力场方向。此次分析中使用了全局网格与局部网格相结合，载具完全展开瞬间的网格划分如图6所示。

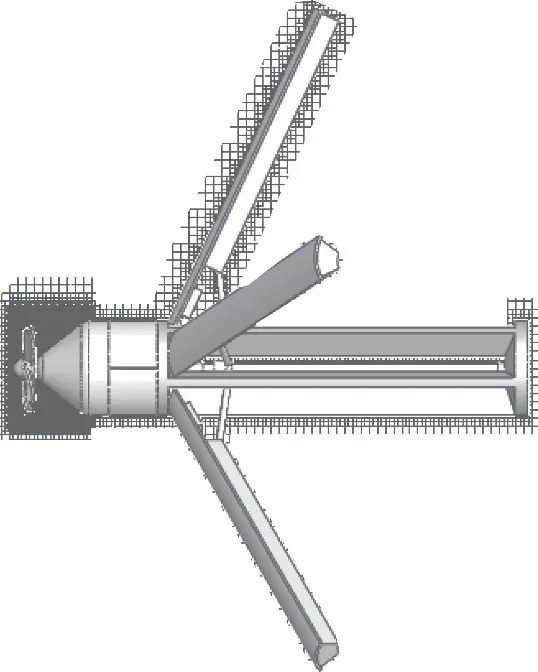
图6 载具完全打开模型与网格分布

在速度100 m/s情况下前端扇叶所产生的扭矩变化趋势，如图7所示。可见在迭代计算初期，扭矩出现峰值后骤然下降，随着迭代次数ξ增加至50次，整个叶片与丝杠的平衡扭矩逐渐趋于一个平稳值1.097 N·m。即载具在100 m/s的飞行情况下展开机构打开，整个叶片可为载荷承载叶展开提供稳定的扭矩Tf，数值大小约为1.1 N·m。

图7 扇叶与丝杠的平衡扭矩

同时针对气动仿真所获得的数据，提取在设定条件下的丝杠扭矩数据点。即保持来流风速v为100 m/s 不变，叶片通过联轴器、扭矩倍增器与丝杠及展开机构风阻力矩达到平衡，为防止载具在风阻作用下其水平速度减小而导致叶片所产生扭矩不足，此时棘轮锁紧机构可提供防回转扭矩。通过迭代收敛计算后，稳定的平衡扭矩即为气动仿真提取点所对应的数值，如图8所示， 其中三维曲面为理论推导所获取的数据网状面，气动仿真提取点较好地显示在网状表面上接近的位置，从而验证了扭矩计算和气动仿真的结果较为吻合。

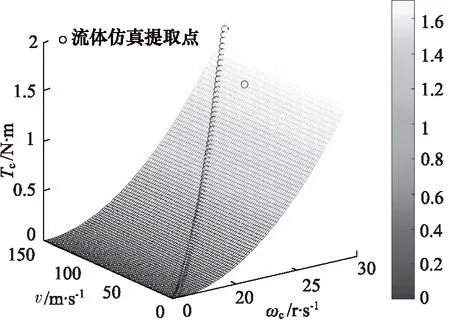
图8 来流风速与丝杠扭矩、丝杠转速之间关系

3 结论

对于风能推动小尺寸叶片经过扭矩放大器，驱动丝杠的扭矩，计算采用叶素理论，经过简化模型与公式推导，给出了扭矩及丝杠转速之间的对应关系，丝杠转速、来流风速增加，丝杠扭矩相应快速非线性增加，验证了计算数据在可行性设计的范围内。载具在100 m/s的飞行条件下，通过Flow Simulation专业流体模块进行气动仿真，可为叶片与丝杠平衡提供稳定的扭矩，为1.097 N·m。通过对比叶素理论与气动仿真计算所得的平衡扭矩，二者较好吻合，从而相互验证了载具在被动式小尺寸扇叶驱动条件下的可行性。