偏导射流伺服阀工作压力形成机理研究

毛麒源， 延 皓， 左哲清， 刘金鑫

(1.北京交通大学 机械与电子控制工程学院， 北京 100044;2.北京精密机电控制设备研究所， 北京 100076)

引言

偏导射流伺服阀也称为偏转板射流阀，由于其转动惯量小，动态响应更迅速，现已被广泛应用于航空、航天领域各类舵机操作系统中[1]。

早期对射流类伺服阀的相关研究大多针对射流管伺服阀。在早期对射流管阀的工作机理研究和建模基础上[2-4]，赵开宇等[5]结合CATIA，ANSYS Fluent，MATLAB等多种数值模拟方式对射流管阀的动态伺服特性进行了仿真分析； 张颖[6]简化了射流过程， 建立了射流管管口与接收器间的伯努利方程，利用流速分布计算了接受孔平面的动压能，通过节流公式计算了工作压力。参考射流管阀的研究方式，訚耀保等[7]改变了偏导射流阀的内部参数和外部条件，对前置级内部流场进行了仿真分析，确定了伺服阀稳态工作压力的主要波动因素。为探究接受腔工作压力形成机理，何文凯等[8]建立了质量-流量方程，基于节流原理研究了气动式伺服阀容腔压力的变化规律。任玉凯等[9]对偏转板不同位移量下的偏导阀前置级流场进行了仿真分析，提出了计算前置级液动力的方法，量化了影响伺服阀工作压力稳定性的因素。LI[10]将接受腔内流体视为运动活塞，把射流模型简化为射流流体与活塞的撞击，通过数值模拟验证了该活塞模型的正确性并计算了腔内压力。SAHA等[11]同样采用活塞模型，对偏转板前置级流场流速分布进行了更细致的描述，验证了在层流和紊流共存的流场下该模型也适用于计算接收腔工作压力。YAN等[12]则将接受腔口平面固化，研究了射流的冲击力分布，基于动量损失原理建立了工作压力方程。

纵观国内外的相关研究，大部分都是基于对偏导射流阀内部流场特性的数值模拟分析，对其工作压力形成机理的研究较少且大多基于节流理论。基于大量的数值模拟工作，本研究将射流对接收腔的作用简化为一种反射机制，推导接收腔压力及压力增益的理论模型，并通过实验方法进行了验证。

1 偏导射流阀

1.1 结构组成

偏导射流伺服阀作为一种两级放大、端口封闭的四通液压伺服阀，在动态响应及控制精度方面表现较为突出，压力和流量的增益线性度也优于其他射流阀。偏导阀的主要组成部分有力矩马达组件、偏导射流放大器件(包括偏转板、射流盘)和滑阀[13]，其整体结构如图1所示。

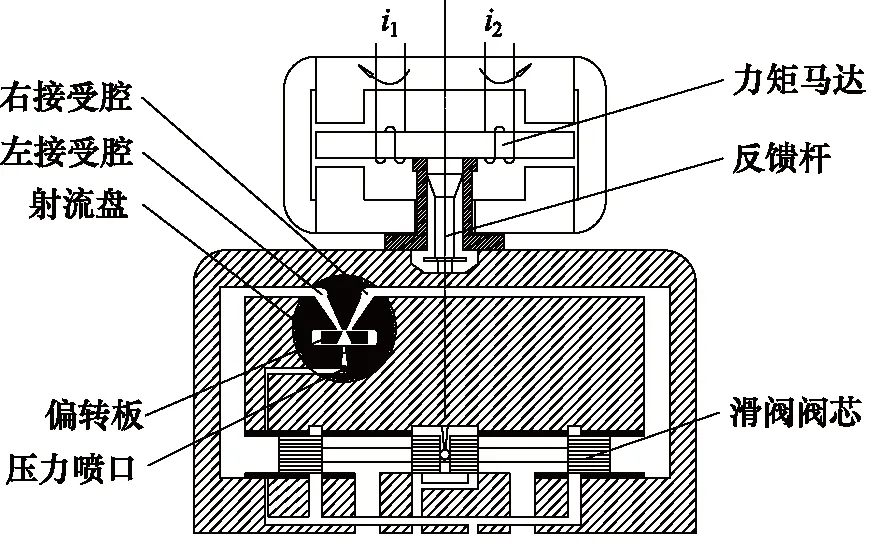
图1 偏导射流阀结构原理图

1.2 工作过程

油路连通时，若控制电流为0，衔铁不偏转，偏转板处于中位，油流从压力喷口进入，流经偏转板均匀地射入2个接收腔内，形成相等的压力，因此滑阀阀芯不产生位移。当有控制电流输入时，衔铁在电流的磁效应下被磁化并发生偏转，带动与之相连的偏转板发生偏转，导致流经偏转板射入左、右接收腔的油液存在差异，在两腔内形成不同的压力，迫使滑阀阀芯运动，从而实现微弱的电信号到液压信号的放大效果。阀芯的位移作用在反馈杆上，产生反馈转矩，当该转矩与输入电流的电磁转矩相等时，阀芯维持在该位置不再运动，使得输出流量稳定。不同大小的控制电流输入会导致不同的阀芯位移量，进而实现对输出流量的比例控制[14-15]。

1.3 2次射流过程

根据YAN[16]偏导射流阀前置级的流动可以划分为2次射流，即由外部直接引入的初始射流，及流经偏转板后的偏转板射流，如图2所示。

图2 偏导射流阀前置级射流过程示意图

在初始射流阶段，高速油液射入偏转板区域，可以视作受限的平面紊动射流，并在偏转板内部形成高压区，完成压力恢复使命。而无论偏转板如何运动，其内部的压力恢复基本不受影响，因此偏转板射流的流速基本稳定。然而，随着偏转板的偏移，2个接收腔之间的分流机构对射流产生影响，引发接收腔压力的区别，从而产生工作压差驱动主阀芯运动。

2 偏转板射流分析

目前，数值模拟依然是研究偏导射流阀的主要手段。考虑到冲击射流存在低雷诺数流动，采用标准k-ε湍流模型是一个较好的选择。随着偏转板的偏移，射流的变化规律见图3。

数值模拟显示， 偏转板射流在分流机构上形成冲击射流，部分流体的流动方向由射流方向转换为平行于冲击平面的方向；当此部分流体流出分流机构，与其他射流方向的流体汇合形成新的衍生射流。该射流以一定的角度射入接收腔，并以近似相同的角度流出接收腔，因此可以看作射流发生反射。从图3中还可看出，当偏转板偏移，射入2个接收腔的衍生射流的方向也发生变化。当偏转板移向一侧，该侧衍生射流垂直于冲击平面的速度分量增大，将对该侧的接收腔产生更大的冲击，另一侧正好相反，2个接收腔的压力由此发生不同的变化(图4)。

图3 不同偏转板偏移量下的速度云图

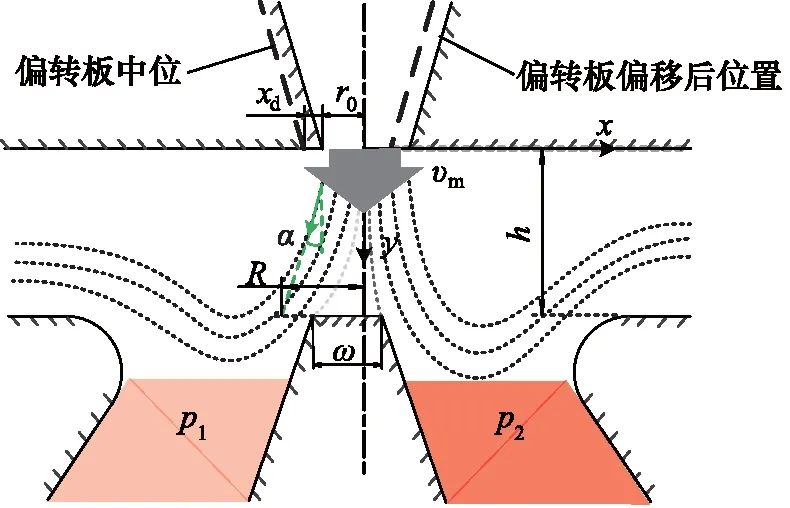
图4 偏转板射流区流场分布示意图

为了解上述过程，首先要作以下假设：

(1) 射流的流速符合高斯分布；

(2) 作用于分流机构冲击平面的流体动量在射流方向上全部消耗。

因此，如果没有分流机构作用，射流的特征半宽将以扩张角α随射流距离向外扩张，在分流机构处的特征半宽是R，即：

R=r0+tanα

(1)

式中，h——射流口距离冲击平台平面距离

r0——射流口半宽

由于符合高斯分布，则射流速度可以表示为：

(2)

式中,υ——射流断面上距离射流中心O距离为x处的流体流速

υm——射流中心最高流速

那么，未撞击分流机构的而直接进入接收腔的部分流体的动量为:

(3)

(4)

式中,M1y,M2y——分别为直接进入左、右接收腔的流体动量

xd——偏转板偏移

ω——冲击平台宽度

与分流机构作用消耗掉的射流方向总动量：

(5)

然而，在分流机构作用下，流体紧贴冲击平面向两侧流动。伴随能量转换和摩擦损失，当流出分流机构时，其水平动量分别为M1x,M2x。

那么进入左、右两腔的总动量为:

(6)

(7)

如图5所示,冲击前后动量变化示意图。

图5 冲击前后动量变化示意图

如果忽略能量损失，并假设流体进入接收腔后发生完全的反射，即流出接收腔的流体动量射流方向分量发生反向，而水平分量不变，见图6。

则流体进出接收腔的动量变化量为:

(8)

(9)

ΔM1=2M1y

(10)

ΔM2=2M2y

(11)

那么根据动量定理:

p1L0=2M1y

(12)

p2L0=2M2y

(13)

式中,p1和p2分别为2个接收腔内压力；L0为接收腔的有效作用长度，其定义和尺寸见图6。

图6 接收腔内的射流反射

则2个接收腔的压力差可以表示为：

(14)

按照式(3)、式(4)和式(14)进行偏导射流阀的压力计算，实际的结构参数见表1。此外，在前期数值模拟中，射流中心最高速度为υm=173.07 m/s，扩张角α=5.64°，液压油密度ρ=849 kg/m3。计算结果见表2，线性拟合后计算的压力增益为207.05 MPa/mm。

表1 偏导阀前置级实际结构参数 m

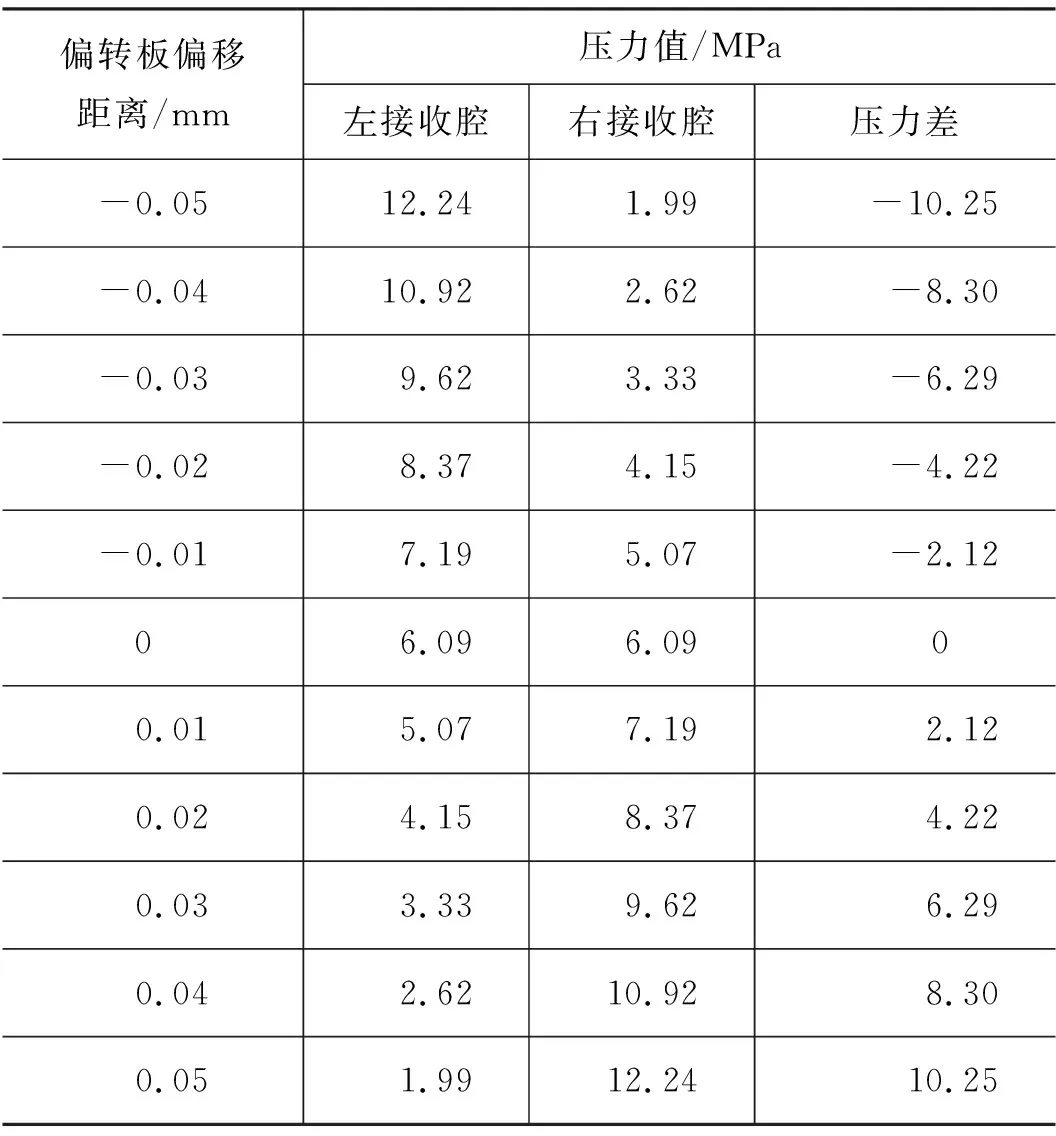
表2 理论模型计算结果

3 模型的实验验证

为验证理论模型的准确性，测量偏转板不同位移量下的两腔实际压力值，实验原理如图7所示。由于偏转板处于射流机构内部，其位移量无法直接测量，但考虑到衔铁组件中的反馈杆与偏转板是直接相连的，因此可以利用位移传感器直接测量衔铁的位移量， 再通过几何关系计算偏转板的位移， 进而建立偏转板位移与两腔压力的特性曲线。通过实验，可以获得偏转板位置变化时左、右接收腔的实际压力值及两腔压力差，如表3所示。

表3 实验结果

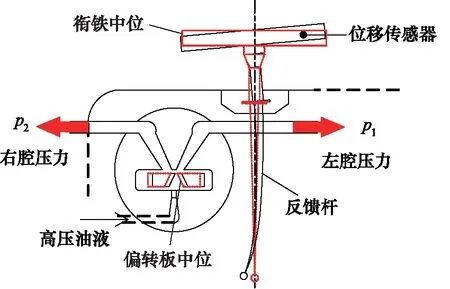
图7 射流盘接收腔压力测量原理简图

对比计算模型与实验中的压差，如图8所示，发现当偏转板位移在±0.03 mm以内时，理论模型的计算结果与实验数据几乎重合；在此范围之外，实验压差的斜率出现轻微的下降。这种现象可以解释为，当偏转板位移较大时，衍生射流的反射过程受到另一侧边界的作用越来越明显，理论模型将出现一定的计算误差。然而，该误差并不大，且更多的情况下伺服阀工作在小开口状态，因此理论模型可以用来进行一般的压差计算。

图8 理论计算与实验数据压差对比分析曲线

此外，通过线性拟合可知在零点附近实际压力增益为203.62 MPa/mm，与理论计算相比偏差约为1.68%。受到机械加工精度的影响，实际结构的尺寸会存在一定的误差，尤其是分流平台的实际尺寸对最终的压力增益有一定的影响。

4 结论

偏导射流伺服阀的射流接收端结构复杂，导致2次射流区流动形态多变。可以认为，2次射流在扩散角的作用下，在到达下方接收腔时，一部分流体的动量保持射流方向不变，另一部分的流体动量在撞击分流平台后转变为水平方向动量，而进入接收腔的流体总动量由这2个分量结合而成。由于接收腔可以看作是具有一定刚性的封闭容腔，对射向其表面的流体具有较为理想的反射作用，而反射所需冲量即接收腔压力的直接成因。基于该原理的数学模型可以用来进行接收腔压力的简化计算，为偏导射流阀的前置级设计提供理论依据。