基于FCM和贝叶斯神经网络的风电功率短期预测研究

文 | 范晓旭，付果，张艳峰，杨锡运

随着环境问题的日益突出，风能作为一种绿色可再生能源已经在世界各国得到广泛应用。但风能的随机性和不稳定性导致风电功率具有波动性和间歇性的特点，使得大规模风电接入给电网安全稳定运行带来一定挑战。准确有效的风电功率预测有助于及时调整调度计划，降低风电并网风险，减少系统备用容量，降低电力系统运行成本。

目前，已有众多国内外学者对风电功率预测做了大量研究工作，主要包括物理预测法和统计预测法。物理预测法利用数值天气预报信息以及风电机组附近的地貌等物理信息建立预测模型，计算过程较为繁琐。统计预测法是指采用数学统计方法建立历史数据与风电功率之间的某种映射关系，以此来进行风电功率预测，现有的统计预测法可分为时间序列法、人工智能法。常用的时间序列法有卡尔曼滤波法和自回归滑动平均（ARMA）法，此类预测方法运算简单，但针对严重非平稳性数据的适应性较弱。人工智能法是指利用智能算法的自学习、自组织、自适应能力实现预测。人工神经网络作为一种具有较强鲁棒性与容错性的智能算法，在风电功率预测领域得到了广泛应用。人工神经网络的泛化能力会受到网络结构（隐含层数、隐含层节点数、隐含层函数）的影响，导致训练结果往往不稳定且易产生过拟合现象，贝叶斯定理能有效克服模型过拟合问题，贝叶斯神经网络BNN（Bayesian neural network，BNN）已在光伏阵列功率短期预测中获得较好的应用效果。此外，训练数据对于人工神经网络的泛化能力有关键影响。由于训练数据间存在较大的差异，通过聚类思想，对聚类后不同性质的训练数据分别建立神经网络模型，能够有效提高建模精度。

本文考虑到风电功率数据存在的时空特性，采用模糊C均值聚类FCM（fuzzy c-means，FCM）来分析风电功率数据，针对经FCM处理后的聚类数据分别建立适应不同功率特性的贝叶斯神经网络预测模型得到风电功率预测值，并对风电功率的预测误差进行分析，采用核密度估计法得出风电功率可能波动范围等更多的预测结果。

理论基础

一、模糊C均值聚类

聚类其实是将一个数据集遵从某种策略分为多个不同的类，达到这样的效果：聚在同一类的样本相似度尽可能高，没有聚在一类的样本相似度尽可能低。1969年，Ruspini首先提出了模糊聚类算法。1974年，Dunn在模糊聚类算法的基础上提出了模糊C均值聚类算法，并得到广泛应用。随后，Bezdek对这种算法进行了推广。

该算法的基本思想为对于一个样本集X＝｛x1,x2,x3,…,xn｝，其中，xi＝｛xi1,xi2,xi3,…,xil｝，i=1,2,…,n（n 为待聚类数据维数），采取聚类算法的规则将其分为规定的c个子集，即Z＝｛z1,z2,z3,…,zc｝，zk（k＝ 1,2,…,c）是c个子集的中心点。模糊聚类算法的目标函数为：

m表示模糊指数，其满足，该值对模糊聚类算法的性能影响很大。dik为点xi到聚类中心zk的距离，这里选择欧几里得距离；uik为点xi到中心点zk的隶属度，满足。隶属度矩阵为：

若要使目标函数达到最小，则隶属度函数与聚类中心点需要满足以下条件：

该算法流程为：

（2）根据公式（3）计算出各数据到各中心点的隶属度值uik，进而得到隶属度矩阵U。

（3）由公式（4）更新聚类中心点zk（k＝1,2,…,c）。

（4）若|J(t+1)-J(t)|<ε或者t>T，则停止迭代，否则t＝t+1，转入流程（2）。

二、贝叶斯神经网络

BP神经网络是一种多层网络的误差反向传播算法。常见的BP神经网络一般有3层：输入层、隐含层和输出层。其算法包括正向传播过程和反向传播过程。

贝叶斯神经网络对BP神经网络的反向传播过程进行了改进，利用贝叶斯定理来计算BP神经网络的参数，其能够处理信息的不确定性，然后对数据信息进行分析并作出推理，同时对部分未知的信息可以采用概率估计表达，然后利用贝叶斯公式对已经发生的概率进行修正，最后再根据期望值和修正概率做出最优决策。其基本思想是：

（1）根据历史数据的已知信息对类条件概率密度参数进行计算，得出其参数表达式和先验概率。

（2）利用贝叶斯公式把步骤（1）所得公式转化成后验概率表达式。

（3）分析处理后验概率后作出判断并进行决策。

设D1,D2,…,Dn为样本空间域S的一个划分，P(Di)为一个样本发生的概率，则对于任一事件x，P(x)>0有：

已知给定的历史数据D，可以利用贝叶斯正则化算法通过最大化后验概率来估计未知参数。即：

为方便计算，对后验概率取对数，得到：

假设其先验概率满足高斯分布，即：

由此可得：

三、非参数核密度估计

在对风力进行预测和误差分析之后，使用非参数估计方法来建立风力预测误差分布模型。非参数估计方法可以在不考虑外部干扰因素的情况下对特定条件执行统计分析，并且可以得到更好的结果。非参数核密度估计（nonparametric kernel density estimation，NKDE）方法是一种非参数估计，它很好地描述了连续密度函数。该方法不会对数据分布添加任何假设，只从数据本身的特征中研究其分布特征。

假设x1,x2,…,xn是由FCM-BNN模型输出的预测值与其所对应的风电功率实际值相减后得到的预测误差序列，则利用核密度估计此误差序列的概率密度函数为：

式中，xi为给定的样本；K(x,h)为核函数；n为样本总数；h为带宽。选择高斯函数作为核函数，其公式如下：

将公式（11）的核函数带入公式（10）后的预测误差概率密度函数可表示为：

模型建立

该模型为双层预测模型：内层模型首先以模糊C均值聚类对风电功率历史数据进行分类，然后用分类好的风电数据来训练贝叶斯神经网络模型，得到各个训练好的贝叶斯神经网络；外层模型将FCM-BNN模型输出的预测功率与实际功率相减，得到功率预测误差序列，再通过非参数核密度估计对功率预测误差序列进行拟合，得到误差序列概率密度函数，在预测误差概率密度函数上选取满足置信度要求的上下分位点，结合FCM-BNN所得预测功率，从而得到预测功率区间，此区间即为最终得出的基于模糊C均值聚类的BNN-NKDE预测功率区间。

采用如图1所示的模型结构进行预测，具体步骤如下：

（1）对风电数据进行预处理，包括补全缺失数据、剔除坏点等。

（2）初始化BNN神经网络模型的参数以及模糊C均值聚类算法的模糊指数、阈值、迭代次数等参数。

（3）根据模糊C均值聚类算法的目标函数公式（1），计算出每次迭代中的目标函数的值，判断是否满足模糊C均值聚类算法迭代条件。

（4）达到终止条件后停止迭代，得到聚类中心C和隶属度矩阵U。

（5）根据聚类中心C和隶属度矩阵U对风电数据进行分类。

（6）将分类好的风电数据带入贝叶斯神经网络模型中，训练得到贝叶斯神经网络模型。

算例验证

以西北某总装机容量为199.5MW的风电场为例，取该风电场的标杆机组2014年8月6日到2014年9月23日的风电数据，时间分辨率为15min，将2014年8月6日到2014年9月6日的数据作为训练集，利用2014年9月7日到2014年9月23日的数据对本文模型进行测试。

一、模糊C均值聚类结果

选取实际风速、预测风速、实际功率作为模糊C均值聚类的聚类中心，即z＝｛z1,z2,z3｝，划定样本子集c＝4，根据公式（2）计算隶属度矩阵值，并根据图1中的FCM算法流程得出聚类结果（如图2和图3所示，蓝、红、黑和黄分别代表某一分类结果）。

二、贝叶斯神经网络点预测结果

把经过模糊C均值聚类分析后的分类风电数据分别作为训练数据带入贝叶斯神经网络，建立不同的贝叶斯神经网络模型。把预测风速Vt+1和Pt（t时刻功率）作为贝叶斯神经网络的输入，待预测时刻的功率Pt+1作为贝叶斯神经网络的输出，带入测试数据对BNN模型和FCM-BNN模型进行检验，其预测结果如图4所示。

表1显示了在相同数据下FCM-BNN模型和BNN模型

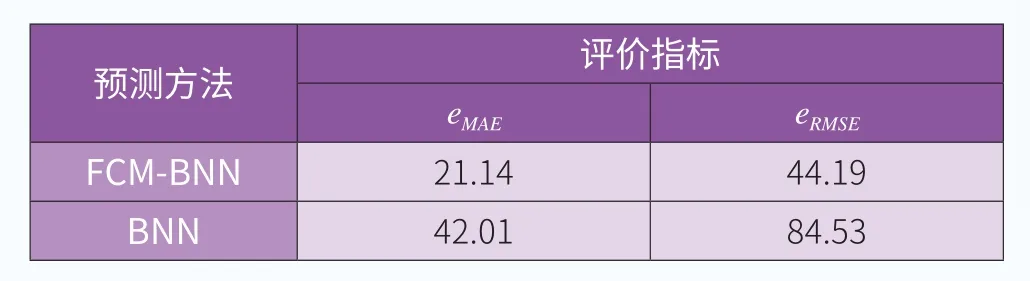
表1 不同点预测方法的误差指标

图4 BNN模型和FCM-BNN模型预测结果所得预测风电功率的平均绝对误差eMAE、均方根误差eRMSE。从误差指标对比来看，FCM-BNN方法的预测精度高于BNN神经网络法。

结合图4分析可知，由于在FCM-BNN神经网络训练过程中对数据进行了分类，使其通过每个分类数据所建立的BNN模型更加贴近实际情况，预测功率的误差更小，预测曲线也能更加贴合实际功率曲线的变化情况。

三、基于NKDE法的功率区间求取

通过上述步骤，将FCM-BNN所得出的点预测功率与实际功率值相减，得到预测误差序列，通过非参数核密度估计该误差序列的概率密度曲线，如图5所示。由图可知，采用非参数核密度估计风功率预测误差所得的概率密度曲线并非呈现出特定的分布曲线，如正态分布等，因此，其相对于参数法能够更好拟合预测误差的实际概率特性，具有更高的建模精度。

为了验证基于FCM-BNN-NKDE区间预测模型的有效性和普适性，将本文提出方法与利用正态分布拟合预测误差的概率分布得出的预测区间进行对比，分别在80%和90%置信度下进行功率预测，结果如图6和图7所示。

表2显示了利用核密度估计法和正态分布预测风电功率区间的覆盖率和平均带宽。由表可知，在80%和90%置信度、核密度估计法和正态分布得出的预测区间的区间覆盖率相接近的前提下，核密度估计法的区间平均带宽指标比正态分布分别降低54.58和23.38，说明核密度估计法得出的预测区间更加准确。从图6和图7可以看出，采用核密度估计法所得的预测区间能够在满足置信度的前提下更准确地包含实际功率，同时随着置信水平的提高，预测区间的范围也相应变宽，这也与理论相符合。

结论

本文考虑到风电在不同功率段下的特性差异，提出了基于聚类分析的贝叶斯神经网络和核密度估计相结合的风电功率区间预测模型。仿真算例表明本文提出的经过聚类分析的点预测方法优于未经过聚类分析的预测方法，针对聚类后的风电数据，贝叶斯神经网络具有更好的泛化能力，从而使得预测精度更高。同时，本文中应用核密度估计法得出风电预测区间的准确性明显高于正态分布法得出的预测区间，说明核密度估计出的预测误差概率分布更加符合真实情况，从而使得预测区间更好地包含了实际功率曲线。