一种多目标引导成像参数和偏流角一体化计算方法

崔本杰 范凯 邓武东 仲惟超 钱丰

(上海卫星工程研究所，上海 200240)

近年来卫星应用的协同化与自主化成为研究的热点，协同化主要体现在多载荷的在轨协同配合[1-2]，如携带电磁探测的载荷可在轨广域搜索实时发现地表目标，实时引导星上成像载荷对目标成像，获取电磁和图像多维目标信息[3]；自主化主要体现在自主成像任务规划[4-5]，卫星需根据多目标信息在轨实时计算成像载荷指向、成像时刻等成像参数，由于星地链路无法做到全时互通，传统地面规划算法多为依赖于地面强大的计算能力[6-7]，受限于有限的星上计算资源，无法应对实时引导成像的参数快速计算需求。在轨自主引导成像任务一般携带小型化的延时积分电荷耦合器件(TDICCD)相机，并可通过摆镜快速调整相机指向目标[8-9]，成像时需要进行偏流角补偿以保证线阵推扫方向与目标像移速度方向保持一致[10-11]。传统的偏流角补偿一般研究依靠卫星姿态机动调整相机指向目标的偏流角补偿问题[12-14]，对于含摆镜相机的偏流角补偿方法研究并不多见[15]。与此同时，携带广域搜索载荷的卫星在执行多目标实时引导成像任务时，视线指向的变化会带来偏流角的变化，星上对成像参数的求解与偏流角的补偿存在耦合[16-17]，短时间内频繁指向改变，可能会导致卫星姿态的频繁抖动，进而影响指向和偏流角修正精度。文献[15]给出了一种基于四元数控制量的摆镜相机偏流角补偿算法，文献[18]提出了一种面向在轨实时引导成像的多星自主任务规划方法，文献[19]论述了侦察卫星引导式协同任务规划模型与算法，但以上研究未给出成像参数求解与偏流角修正的耦合问题的解决方法。

针对上述多目标引导成像参数星上实时计算与偏流角控制的耦合问题，本文首先进行多目标引导成像任务特点分析，提出了一种成像参数计算及偏流角控制一体化方法，然后给出在轨验证情况和后续发展建议。

1 多目标引导成像任务特点

对于同时携带广域目标搜索载荷和光学成像载荷的一类卫星，执行自主成像任务规划，广域目标搜索载荷可实时进行多目标搜索定位，生成目标引导队列，并结合卫星当前轨道、姿态、载荷安装等信息，在轨计算目标指向及成像时刻，对于携带TDICCD推扫相机并依靠摆镜绕滚动轴摆动实现对地视场横向扩展的卫星，目标指向需转换为摆镜角度，如图1所示。

图1 广域搜索引导成像示意图Fig.1 Schematic diagram of wide-area search guided imaging

多目标引导成像过程中，须完成对轨道内所能观测到的多个目标进行成像，随着卫星向前飞行，卫星沿航迹向前推扫，在将要遇到目标之前，通过摆镜调整视场对准目标方向，同时依靠姿态绕视轴实时修正偏流角，单次成像完成后，可继续对多个地面目标进行成像，如图2所示。

图2 多目标连续成像示意图Fig.2 Multi-target continuous imaging

2 成像参数计算与偏流角补偿方法

考虑到目标经纬度通常在地球固联坐标系(一般为WGS84系)描述，传统的计算方法多应用J2000轨道参数[6,12]，坐标系转换过程存在精度损失，因此采用星载导航接收机易于获取的WGS84系轨道信息，选择真赤道面为参考基准建立瞬时惯性系，统一描述下的成像参数和偏流角计算模型，与目标地理经纬度统一了参考框架，计算复杂度低；建立统一的成像参数计算与偏流角控制公共变量，进行基准姿态角和偏流角偏差的迭代计算与补偿控制，给出绕瞬时虚拟光轴旋转的偏流角补偿方法，可更好的适应摆镜的连续摆动，得到平缓的偏流角控制目标值用于姿控跟踪。

下文给出多目标实时引导成像参数及偏流角一体化计算方法的推导过程，参照文献[9]的轻小型相机模型，首先给出坐标系定义及含摆镜相机的等效光路模型，以WGS84位置速度建立瞬时惯性系，在该坐标系下以目标经纬度为输入，给出目标成像参数及偏流角的计算方法，最后给出成像参数求解及偏流角补偿一体化控制流程。

2.1 坐标系定义及含摆镜相机的等效光路

建立描述从成像点到像点映射相关的坐标系，包括瞬时惯性坐标系、卫星轨道坐标系、卫星本体坐标系、虚拟相机坐标系、虚像平面坐标系，并定义卫星、地面目标、地心三者间的矢量。

瞬时惯性坐标系OeXiYiZi，OeXi轴在地球赤道平面内，指向导航数据时戳时刻的WGS84坐标系X轴方向；OeZi轴垂直于地球赤道平面，与地球自转角速度矢量方向一致，OeYi与OeXi、OeZi轴垂直，且构成右手坐标系。卫星轨道坐标系OsXoYoZo，Os表示原点，即卫星质心，OsXo轴在卫星轨道平面内，指向卫星的运动方向，OsZo轴指向地心，OsYo与OsXo、OsZo轴垂直，且构成右手坐标系。卫星本体坐标系OsXbYbZb，OsXb轴沿卫星飞行方向，OsZb轴与OsYb轴、OsXb轴构成右手坐标系，当卫星处于标称零姿态运动时，OsXb、OsYb、OsZb轴分别与OsXo、OsYo、OsZo轴平行，且方向相同，如图3所示。

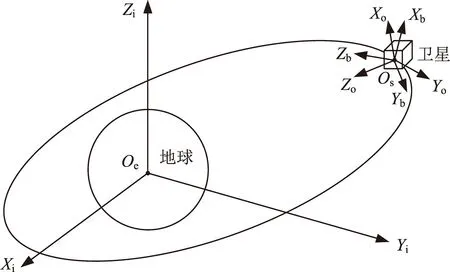
图3 惯性、轨道、本体坐标系定义Fig.3 Coordinate system definition of inertial,orbit and satellite body

光学相机安装在卫星对地面上，定义虚拟相机坐标系OcXcYcZc，Oc表示原点，即摆镜虚相机的摄像中心，OcXcYc平面为物镜平面；OcZc轴沿光轴方向，摆镜无摆角时OcXc、OcYc轴与卫星本体坐标系OsXbYbZb重合，如图4、图5所示，构成右手坐标系。

虚像平面坐标系OpXpYpZp，Op表示原点，即相机像平面光轴中心处；相机像平面法线与OcZc轴平行，且OpXp、OpYp轴分别与OcXc、OcYc平行，且方向相同。TDICCD芯片积分方向沿OpXp方向，当摆镜摆过φB角后，相当于相机摆过2φB角[16]，如图5所示。

因此，带摆镜的TDICCD相机等同于对地相机，此相机可绕本体X轴以二倍摆镜摆角偏置，以扩展对地视场。

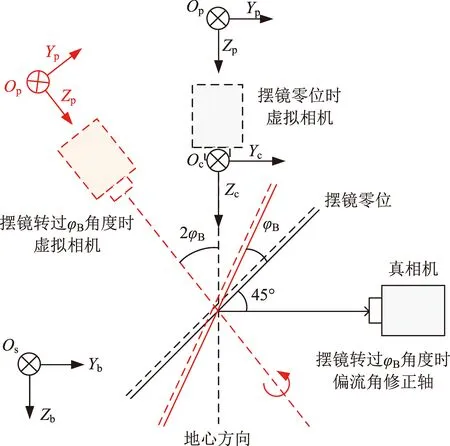
注：Xp、Xc为垂直于纸面向内。图5 镜面反射后的虚拟光轴Fig.5 Mirror reflection of the virtual camera

2.2 成像参数及偏流角补偿一体化计算流程

卫星执行多目标成像时，由摆镜机构完成成像视场调整，实时进行成像点偏流角修正，为获得清晰图像，由姿轨控修正摆镜摆角变化引起的偏流角偏差。姿态角测量值和摆镜摆角测量值通常包含控制延时和噪声，而偏流角补偿是一个随着轨道位置变化的动态负反馈过程，若使用测量值，其动态过程可能会导致偏流角控制目标的抖动。由于姿态角速度为随机分布小量，且受控制系统带宽限制无法实时跟踪，可忽略其对偏流角的影响[12]，也可避免姿态角剧烈抖动时，偏流角解算送给姿控跟随不确定的角度值，姿态发散的风险。

为描述成像参数及偏流角补偿一体化计算流程，对所用到的参数作如下定义。

(1)基准姿态角：记录目标引导成像参数解算时刻的姿态角测量值，随着新目标引导信息求解动态更新后保持，作为偏流角计算的输入和姿轨控偏流角跟踪的基准。

(2)基准摆角：记录目标引导成像参数解算的摆镜角度结果，作为摆镜角度控制目标量，是偏流角计算输入和姿轨控偏流角跟踪的基准。

(3)姿态角测量值：卫星三轴姿态角测量值，作为积分时间计算输入，是目标引导成像参数解算输入。

(4)摆角测量值：摆角机构码盘测量值，作为积分时间计算输入。

(5)偏流角控制四元数：姿态控制补偿的目标量，由基准姿态角、基准摆角、偏流角偏差计算得到。

成像参数及偏流角补偿一体化计算过程变量及信息流如图6所示，导航接收机获取的轨道和姿轨态测量值作为成像参数求解和偏流角计算的公共输入，成像参数求解得到的基准姿态角、基准摆角作为偏流角计算和偏流角跟踪公共输入。卫星在轨引导成像任务初始状态时，星上姿态控制基准通常为三轴0姿态，摆镜角度处于0位，此时三轴基准姿态角和基准摆角均为0，启动偏流角补偿控制，此时随着卫星飞行，卫星姿态将绕视轴变化，当目标出现后，星上根据实时姿态角测量值、目标位置、轨道计算过顶时刻和摆镜角度，当目标满足成像约束时，更新基准姿态角为该目标解算所用姿态角测量值，更新基准摆角为该目标解算所用摆角测量值，偏流角计算采用基准姿态角和基准摆角为输入，可以得到相对平缓的偏流角控制目标值用于姿控跟踪。此后随着新目标的发现，多目标指向切换过程中，基准姿态角、基准摆角动态更新。

成像参数及偏流角补偿一体化计算过程变量及信息流如图6所示。

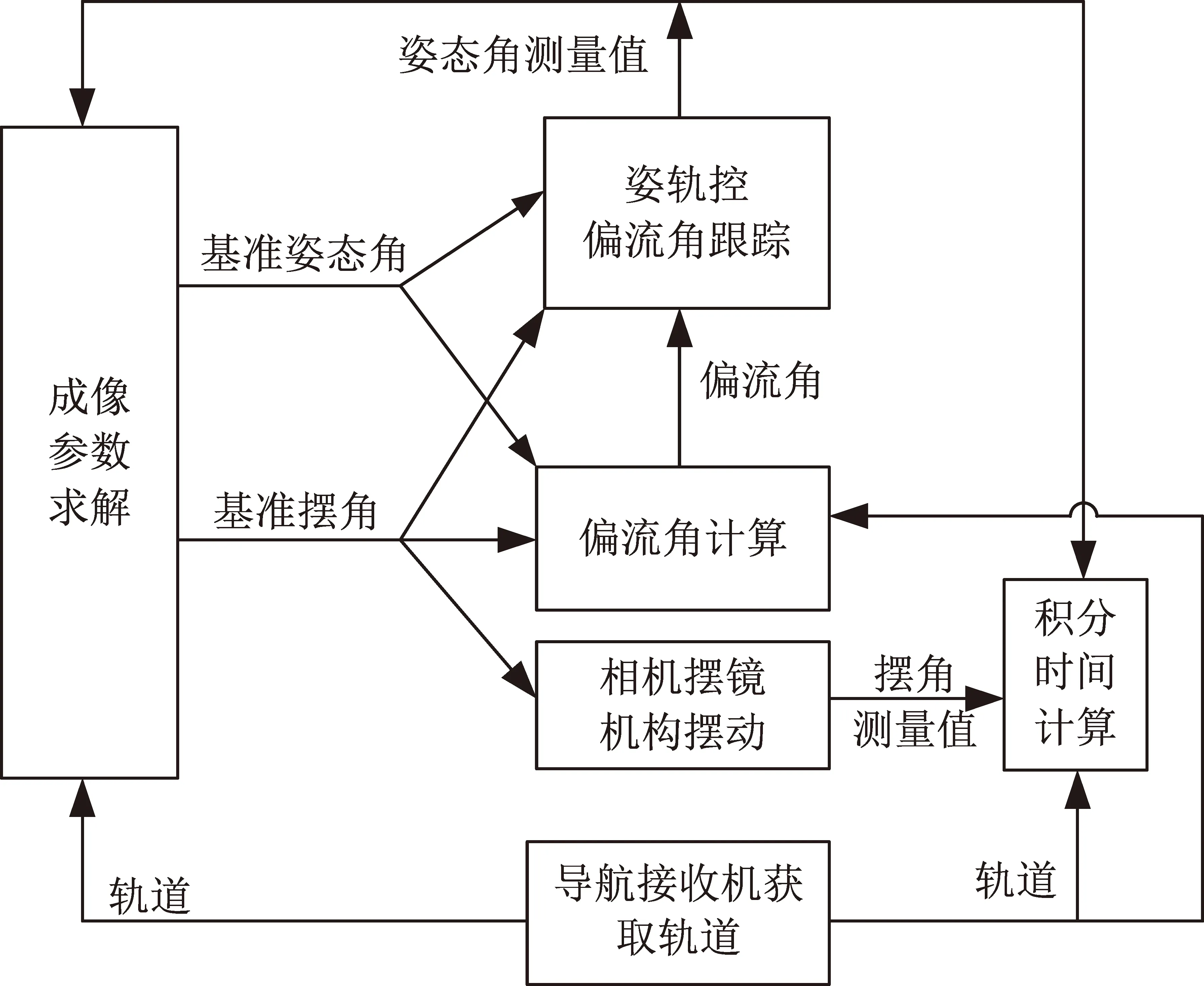
图6 成像参数及偏流角补偿一体化计算过程Fig.6 Integrated calculation process of imaging parameters and drift angle compensation

传统的偏流角修正是绕着卫星偏航轴进行姿态补偿，要求卫星偏航轴(Zb轴)与光轴时刻重合，带有摆镜的卫星的成像光轴随摆镜运动而变化，这种方式并不适用。图5给出了偏流角修正轴，为当前摆镜摆角状态下的虚拟光轴。此时以四元数来描述姿轨控的跟踪指令更加方便，且不存在欧拉角姿态转序问题。设当前时刻的滚动、俯仰、偏航三轴基准姿态角为φ、θ、ψ，对应的相对轨道坐标系的四元数为

qR=

(1)

根据收到的偏流角β和摆镜摆角φB，计算当前控制周期的偏流角偏差四元数为

(2)

参考文献[20]的四元数乘法运算规则计算qR左乘qT，计算结果qC为偏流角控制四元数，可表示为如下分量形式

(3)

根据期望姿态四元数计算基准姿态角

φ=arcsin (2q2q3+2q0q1)

(4)

(5)

(6)

将偏流角控制四元数送姿轨控用于姿态控制的目标量，可以适应星上摆镜的连续摆动，得到平稳的姿轨控姿态控制目标值。

2.3 成像参数计算过程

像移速度计算参考文献[12]的矢量椭球法，并在此基础上以卫星工程上常用的WGS84系位置、速度、姿态角、相机摆角等信息，进行以下推导过程。定义地面目标t：Ret用于描述地面目标，表示从地心指向地面目标的矢量；Res表示从地心指向卫星质心的矢量；Rst表示从卫星质心指向地面目标的矢量；Rct表示从相机指向地面目标的矢量。

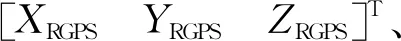
(7)

式中：ωe表示地球自转角速率。

计算卫星轨道角动量

(8)

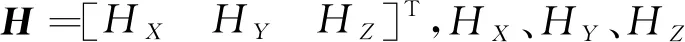
求解OeXiYiZi系下卫星的倾角为

(9)

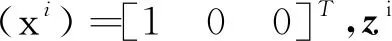
(10)

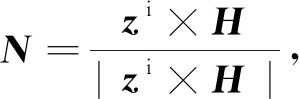
轨道角速度为

(11)

求解TGPS时刻的轨道幅角为

(12)

(13)

轨道幅角为

u=u0+ωT

(14)

式中：T表示从起始时刻开始的时间差。

设CX(α),CY(α),CZ(α)为绕被转动的坐标系轴的旋转矩阵，则

Aoi=CZ(u)CX(I)CZ(Ω)

(15)

(16)

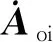
Abo=CY(θ′)CX(φ′)CZ(ψ′)

(17)

式中：θ′表示实时俯仰姿态角，φ′表示实时滚动姿态角，ψ′表示实时偏航姿态角。

地面目标在瞬时惯性坐标系下的坐标和变化率随时间变化的表达式为

(18)

(19)

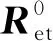
计算地面目标在卫星本体坐标系下的位置和变化率随时间变化的表达式

(20)

(21)

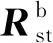
根据卫星本体坐标系下的坐标和变化率随时间变化参数建立约束方程，并求解出成像任务参数，所述成像任务参数包括相机指向调整参数和成像开始时刻。

假设相机安装后视角为θ1，建立约束方程为

(22)

将约束方程转换为F(T)=0的函数，函数表达式为

(23)

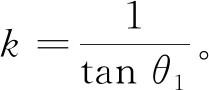
求解函数F(T)的零点，过程如下。

对函数F(T)进行求导运算，得到如下的方程

(24)

利用牛顿迭代求解法计算时间变量T，计算公式为

(25)

求解卫星成像任务参数，包括摆镜摆角φB和相机成像时间TShoot。

若需要提前n秒成像，则相机成像时间为

TShoot=TGPS+T-n

(26)

摆镜摆角为

(27)

2.4 偏流角计算过程

偏流角是目标在像平面投影的像移速度矢量，与CCD阵列的列向夹角，如图7所示。

偏流角受如下因素影响[12]：①轨道运动，卫星高速飞行，给像点在像平面像移速度矢量的贡献最大；②地球自转，地球自转引起不同纬度地面不同的线速度，局部还受高程影响；③姿态运动，卫星姿态角、姿态稳定度决定偏流角计算的基准和成像清晰度；④载荷指向，载荷安装及摆镜指向决定视线在卫星本体指向；⑤目标运动，曝光时间里物体在地表的相对运动；⑥大气折射，大气折射使成像光路非直线；⑦平台振动，卫星平动和转动的高频部分，焦面相对于摄影中心的抖动。其中，目标运动在轨难以预知，大气折射影响较小，平台振动通常由振动抑制及载荷器件补偿，因此工程上的偏流角计算，一般只考虑轨道运动、地球自转、姿态运动、载荷指向等因素。

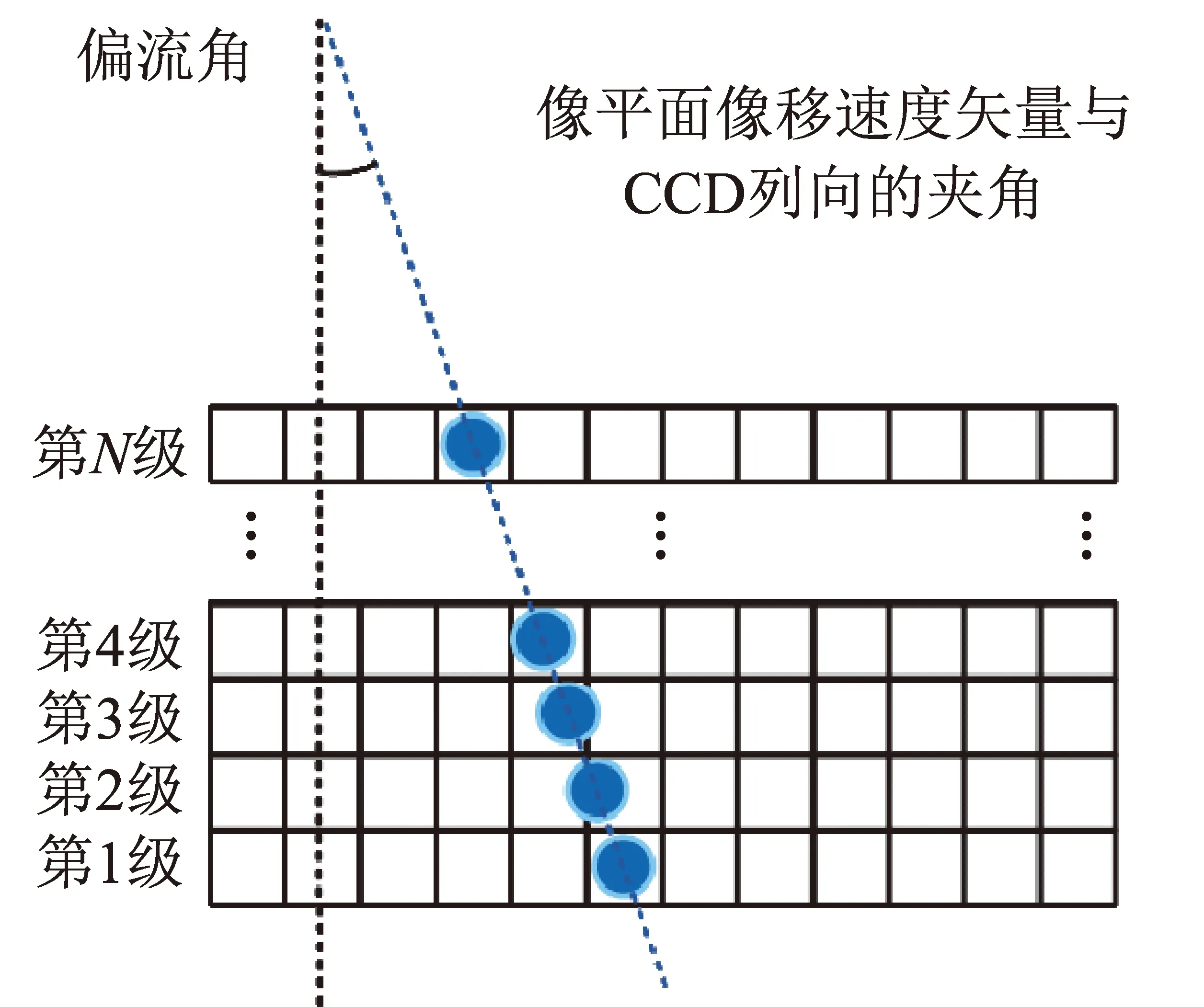
图7 偏流角物理意义Fig.7 Physical meaning of deflection angle

由于卫星成像为大尺度问题，这里假设卫星中心与相机中心重合，相机安装沿体轴方向，忽略各类安装偏差。

从卫星本体系到虚拟相机系的转换矩阵为

Mcb=CX(2φB)

(28)

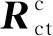
(29)

式中：f为焦距，h为物距。

下面计算经光学系统折反射后，在像平面点在地球上的位置坐标，关系式为

(30)

式中：Mbc=McbT，代表相机系到本体系转换矩阵，Aio=AoiT,代表轨道系列惯性系转换矩阵，Aob=AboT，代表本体系到轨道系转换矩阵。

目标在相机坐标系的变化率为

(31)

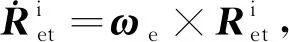
(32)

(33)

β=arctan (Vp2/Vp1)

(34)

3 在轨验证

本文提出的方法在浦江一号(PJ-1)卫星上得到了应用，PJ-1卫星对星上实时引导成像自主任务规划做出了技术探索和在轨验证，2015年9月25日成功发射，卫星质量347 kg，运行在轨道高度约481 km的太阳同步轨道[8]。卫星携带广域搜索电磁信号监测载荷，实现对地面1800 km范围的U频段电磁辐射信号的接收、定位并用于引导相机成像；光学成像为离轴三反TDICCD线阵相机，采用一维机构驱动摆镜快速指向目标区域并进行可见光成像，地面成像分辨率优于3 m，相机瞬时成像幅宽24 km、扫描幅宽550 km；星载图像处理载荷实现对目标的快速自主识别、高精度定位。相关技术已得到在轨验证[8-9,21]。多目标引导成像参数及偏流角一体化计算方法依托星上P1750处理器(主频16 MHz)有限的处理资源得以在轨运行，在轨控制周期0.5 s。

3.1 不同摆角下的偏流角整轨变化情况

在姿态角为三轴零姿态情况下，设摆镜摆角为15°、7.5°、0°、-7.5°、-15°时，偏流角如图8所示。

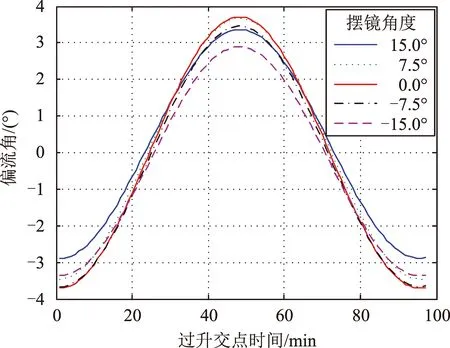
图8 不同摆角下的偏流角Fig.8 Drift angle various with the change of swing angle

图8中，卫星初始时刻处于轨道升交点，仿真了先升轨再降轨的一个轨道周期，可以看出，偏流角全球成正弦规律变化。由于摆镜的动作引起了同一个位置偏流角的改变,表1给出了不同摆角下的偏流角的极值。

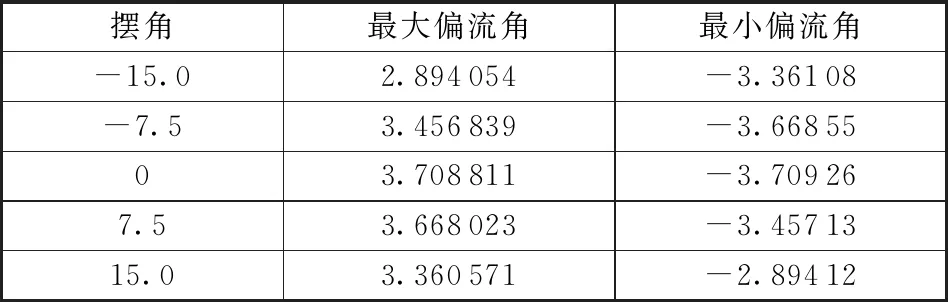
表1 不同摆角时的偏流角极值Table 1 Drift angle extreme value various with swing angle (°)

3.2 多目标连续成像工况

选取在轨境内工况进行分析，该场景卫星降轨飞过北纬30°附近，地面7个目标用以验证引导成像算法、偏流角计算和补偿方法的有效性。目标分布如图9所示。

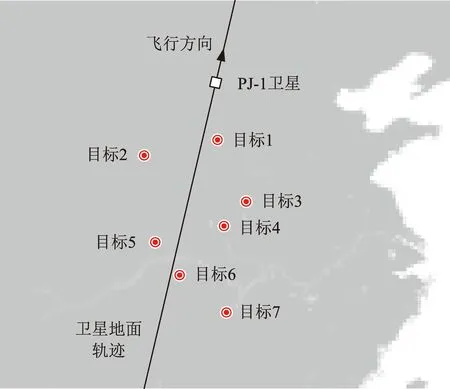
图9 在轨目标分布Fig.9 Distribution of in-orbit targets

卫星在初始状态和末状态时，三轴基准姿态角为0°，摆镜摆角0°，过程跟踪7个目标，卫星摆镜指向目标并跟踪偏流角。表2给出了多目标引导成像目标分布和解算结果，图10给出了摆镜摆角变化曲线图。

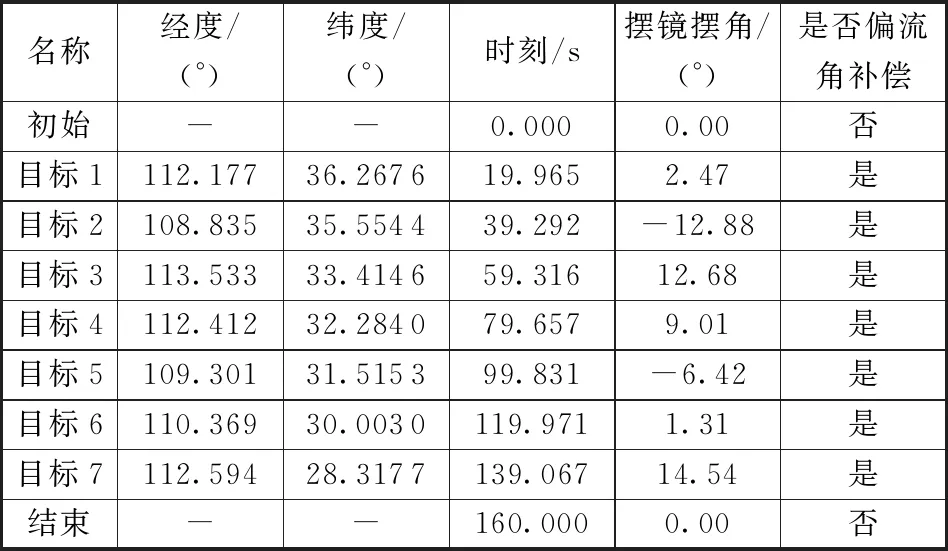
表2 多目标引导成像目标分布和解算结果Table 2 Multi-target guided imaging target distribution and resolution results

图11给出了偏流角偏差随摆镜工作时序变化情况，可以看出未修正偏流角时，偏流角偏差在3°～3.5°之间，在开始跟踪偏流角后，每次摆镜动作时，引起了0.5°内的偏流角偏差突变量，可在2个节拍内将偏流角偏差修正到0°附近。

图12给出了基准姿态角的变化情况，在不跟踪偏流角时，三轴基准姿态角均为0°，卫星本体系的控制目标为与轨道坐标系重合的正对地姿态。第19.965 s开始跟踪偏流角后，卫星基准姿态角随着摆角变化而变化。由于虚拟光轴因摆镜摆角而改变，此时的基准姿态角控制目标在3个轴都有分量，卫星进行了绕虚拟光轴的偏流角偏差修正。

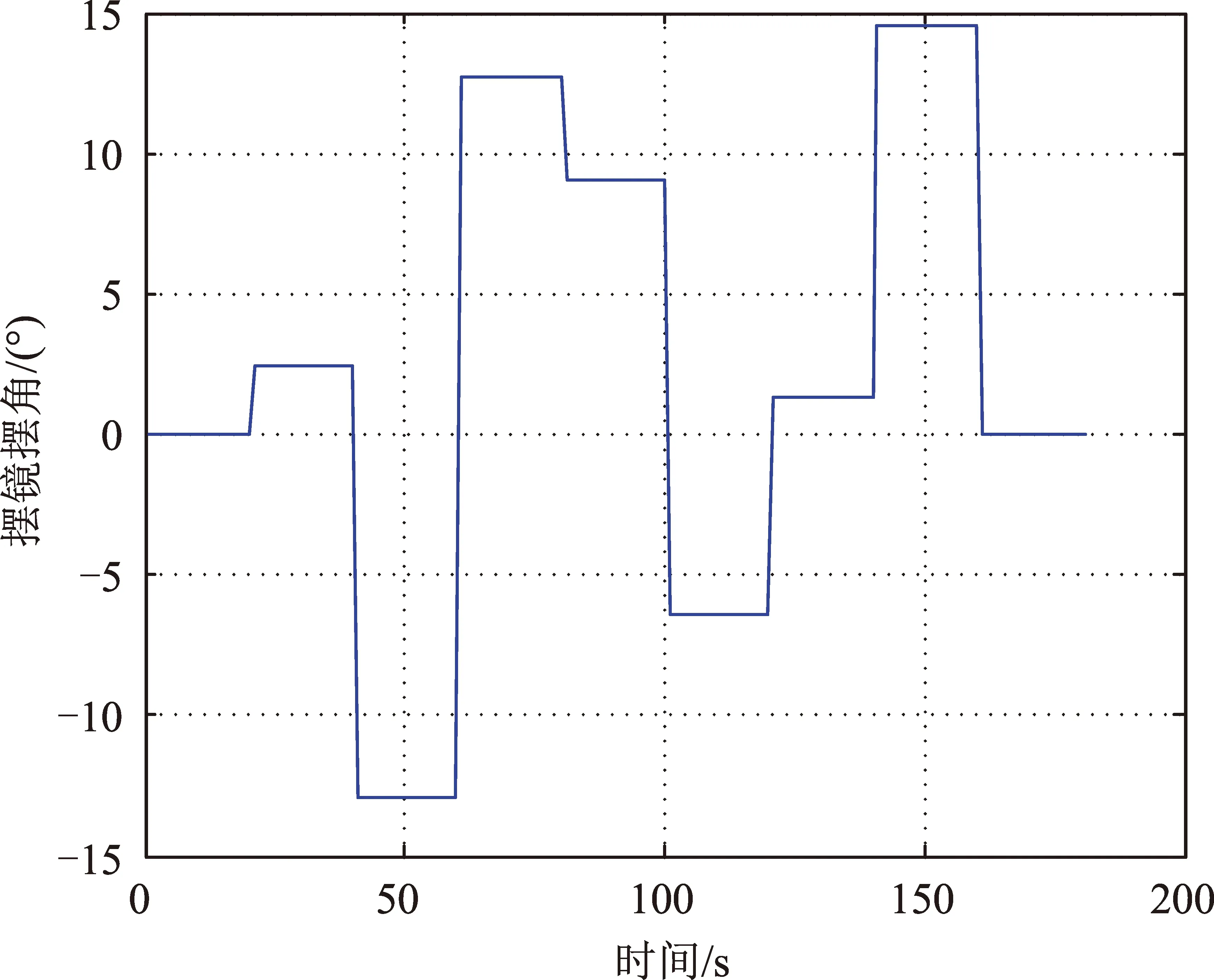
图10 摆镜摆角变化曲线图Fig.10 Swing angle of the swing mirror

图11 偏流角偏差随变化曲线图Fig.11 Drift angle bias graph

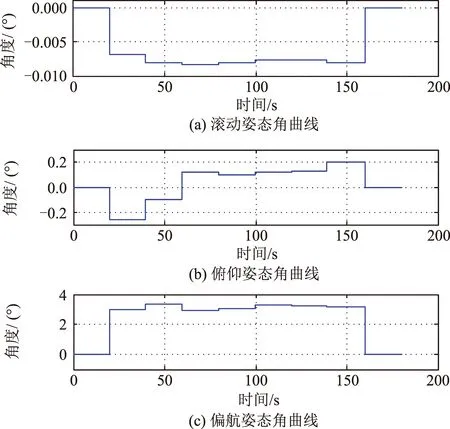
图12 三轴基准姿态角曲线图Fig.12 Expected three-axis attitude angle graph

卫星姿态控制系统需要在一定时间内完成偏流角的跟踪，由图12可以看出，典型工况下姿态角控制的变量在0.5°以内，有利于卫星平台控制系统在较短的时间内跟踪到位。

4 结束语

本文针对多目标引导成像参数计算与偏流角控制的耦合问题，提出了一种多目标引导成像参数及偏流角一体化计算方法，给出了带摆镜的TDICCD相机的等效光路成像模型及成像参数求解及偏流角补偿一体化控制流程。以WGS84系位置速度建立瞬时惯性系，在该坐标系下以目标经纬度为输入，选择基准姿态角、基准摆角等作为统一的成像参数计算与偏流角控制公共变量，推导了成像参数求解和偏流角的计算过程，给出绕瞬时虚拟光轴旋转的基于偏差四元数的偏流角补偿方法。经过PJ-1卫星在轨飞行验证，该方法可以有效的解决含摆镜的TDICCD推扫相机对多目标连续成像的偏流角补偿问题，能够适应星上摆镜的连续摆动，得到平缓的偏流角控制目标值用于姿控跟踪。本方法具有工程实用价值，可为同类成像卫星工程应用提供技术参考。