基于Cesium的卫星载荷可视化仿真分析平台

苏昊翔,董正宏,杨 帆,刘立昊

(航天工程大学 航天信息学院,北京 101416)

0 概述

卫星载荷是卫星用于完成具体任务的实体,卫星载荷的覆盖范围决定卫星完成任务的时间与效率。随着航天技术的快速发展,卫星在我国经济建设和国防建设等领域中的应用日趋广泛[1]。通过动态可视化模拟,能够使用户更直观地判断卫星载荷的运行情况及其与地面间的覆盖关系,从而进一步对载荷及数据进行分析。同时,通过WebGL技术[2]所开发的仿真可视化平台,使得用户通过浏览器即可以进行仿真[3],大幅提高了仿真的便捷性。

目前,对卫星载荷的可视化仿真及过境分析主要是利用特定平台下的软件进行。文献[4]基于Vega Prime和OpenGL进行卫星轨道及载荷的可视化仿真,同时利用HLA体系分散模型计算,避免了单一节点超负荷的现象。文献[5]基于Unity3D引擎设计一种星地监控可视化系统,利用实时生成的卫星参数展示卫星及载荷的多维运行状态。文献[6]通过使用Unity3D脚本实现了对地面覆盖区域的绘制。文献[7]以OSGEarth为底层平台开发卫星轨道及载荷可视化支撑平台,同时通过选择性绘制卫星轨迹,降低了客户端的计算量。文献[8]使用C#对STK进行调用,通过STK[9]计算相关数据并在ArcGlobe平台中进行显示。文献[10]基于Qt平台构建了卫星覆盖性分析软件,同时利用插件技术提高了软件的复用性。

上述研究虽然完成了卫星载荷可视化及过境分析,但都需要在平台上单独安装相应软件,难以实现跨平台使用,并且仿真数据结果及可视化仍需使用特定软件进行展示,不利于仿真结果的可视化共享,对于仅需要仿真可视化结果的用户来说提高了使用成本。同时由于将数据计算与实时渲染放在同一硬件中实现,对仿真硬件的要求也较高。本文基于Cesium[11]三维GIS框架构建一种可以通过浏览器直接使用的卫星载荷可视化仿真分析平台,采用四维变换矩阵对卫星载荷边界可视化仿真及过境分析过程进行准确计算,同时以JSON格式对场景数据进行保存与读取,实现仿真数据的共享。

1 平台架构及功能模块设计

基于Cesium的卫星载荷可视化仿真分析平台采用B/S架构[12],如图1所示。

图1 平台系统架构Fig.1 System structure of the platform

系统整体分为数据层、支撑层、业务层及表现层4层结构。其中:数据层用于存储和管理基础地理信息数据、卫星轨道计算模型、载荷计算模型以及过境分析模型4类基本数据;支撑层为平台提供了基础框架,通过采用“平台+插件”的技术框架,使用Cesium基础平台,提供GIS功能、API以及程序开发框架,同时利用功能插件对轨道、路径、载荷以及分析等数据进行计算;业务层是系统的核心部分,通过基础操作服务、地理信息服务、数据可视化以及数据分析计算4个模块为表现层提供业务支持;表现层是展示给用户的界面,用户可以使用浏览器对系统进行访问,通过人机交互操作对卫星载荷及过境分析进行可视化仿真。

在卫星载荷可视化及过境分析过程中,无论是进行卫星轨道数据的递推还是计算载荷覆盖区域,都需要进行大量的数据运算。同时,在3D可视化[13]渲染过程中也会进行大量的运算。如果将这些运算都集中在客户端,会对客户端硬件带来巨大的压力,不但会大幅降低数据计算的速度,而且还会影响可视化结果的显示。

如图2所示,平台将主要功能模块分别部署在用户端及服务器端。交互控制模块主要用于用户输入仿真参数并对仿真场景进行控制与编辑,而可视化模块主要用于仿真数据的可视化分析,从而为用户提供直观的仿真结果,因此,这两个模块使用JS实现并部署在用户端。数据计算分析模块主要对仿真数据进行计算,通过搭建计算服务器,用于卫星轨道递推、目标路径计算、载荷覆盖范围计算[14]以及过境分析等大量复杂数据运算,同时利用AJAX技术[15]进行客户端与服务器端的数据交换,从而将复杂数据计算与可视化化渲染相分离,减轻客户端的计算压力,提高仿真效率。

图2 系统功能模块Fig.2 System function module

2 平台功能实现

2.1 数据计算与渲染分析模式

在可视化仿真分析过程中,需要进行大量的数据计算,同时还要对结果进行实时可视化渲染,因此,为减低客户端计算压力,本文采用数据计算与渲染相分离的模式,用户通过浏览器,仅需调用服务器API即可获取数据计算结果。

以卫星轨道仿真为例,卫星轨道计算及其可视化过程如图3所示。用户可以直接通过如图4所示的用户交互界面输入卫星轨道参数,浏览器通过AJAX服务将卫星参数传输至计算服务器,计算服务器通过调用轨道计算模型库中的模型,对卫星轨道进行递推,计算出仿真时间内每一时刻卫星在惯性坐标系下的轨道位置,并将计算结果返回浏览器端,浏览器通过在Cesium框架中添加卫星实体实现卫星轨道可视化并将结果呈现给用户。

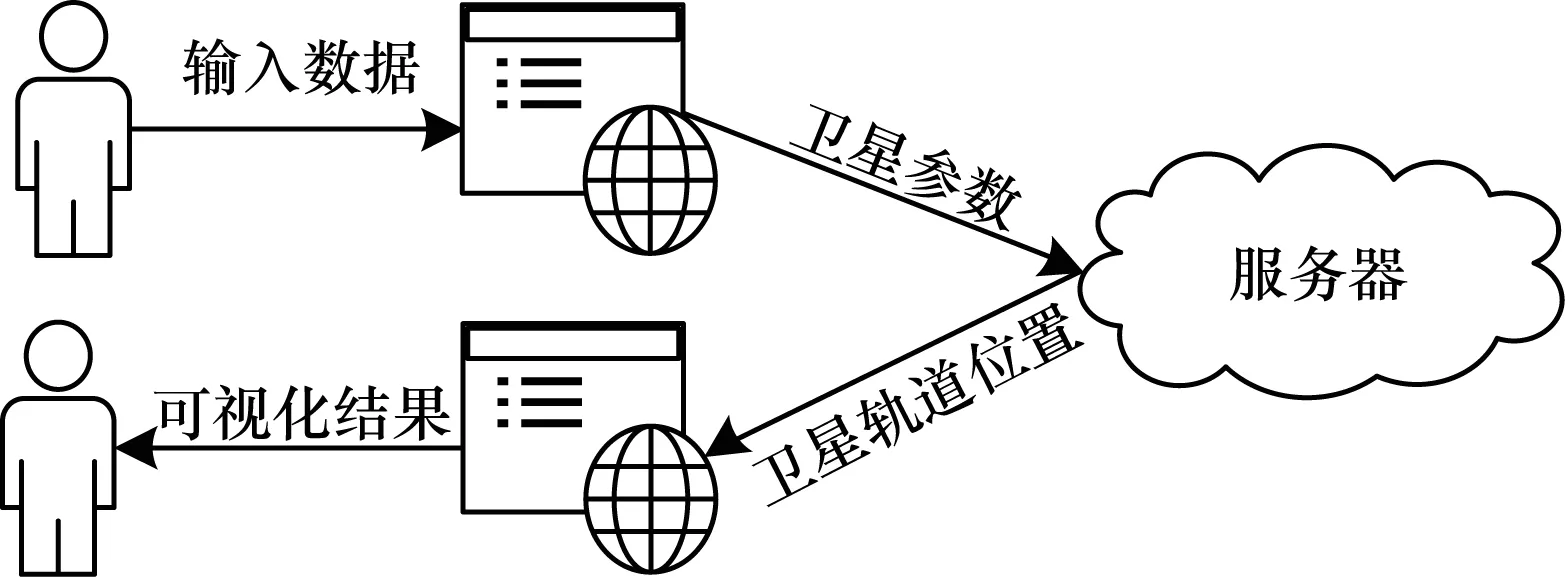
图3 卫星轨道计算及其可视化过程Fig.3 Satellite orbit calculation and its visualization process

图4 卫星参数采集界面Fig.4 Satellite parameter acquisition interface

平台可视化结果如图5所示。其中,图5(a)为卫星轨道三维可视化结果,图5(b)为卫星轨道二维可视化结果。平台通过Cesium所提供的API接口为用户提供不同投影方式,用户可以通过场景切换按钮分别查看仿真数据在三维、二维及哥伦布投影中的不同可视化结果,从而直观地从多角度展示仿真数据,更好地为用户提供决策所需信息。

图5 卫星仿真可视化结果Fig.5 Visual results of satellite simulation

2.2 基于四维矩阵的载荷覆盖区域及过境分析计算

2.2.1 基于四维矩阵的载荷覆盖区域计算

卫星载荷在仿真时一般可等效为矩形载荷[16]及圆形载荷[17],即将载荷覆盖等效为一个顶点在卫星所在位置的四棱锥或圆锥。现阶段,对于载荷覆盖区域计算一般都采用根据卫星与边界载荷覆盖边界间的关系直接计算载荷边界覆盖点所在的经纬度坐标,但这种方法需要进行多次坐标转换[18],计算复杂,同时仅对未进行三维旋转的载荷有较好的计算精度,对于经过三维旋转的载荷,计算更为复杂,且精度较低,因此,本文采用一种基于四维转换矩阵[19]的载荷覆盖区域计算方法。该方法能够精确地对所有类型载荷覆盖范围进行有效计算,同时其四维转换矩阵还可应用于过境分析检测。

如图6所示,本文首先通过在载荷坐标系下建立高为1的单位载荷模型,并根据载荷类型及其视场角大小,分别计算出以卫星为原点的载荷边界向量坐标;然后通过当前时刻卫星轨道位置、卫星三维旋转角及载荷三维旋转角,计算出当前时刻将载荷边界向量从载荷坐标系下转换至地固坐标系下的四维变换矩阵;再通过所计算的变换矩阵,将载荷边界向量坐标转换至地固坐标系下;最后通过建立载荷边界向量方程,计算其与地球椭球的交点,从而获取载荷边界点在地固坐标系下的坐标。

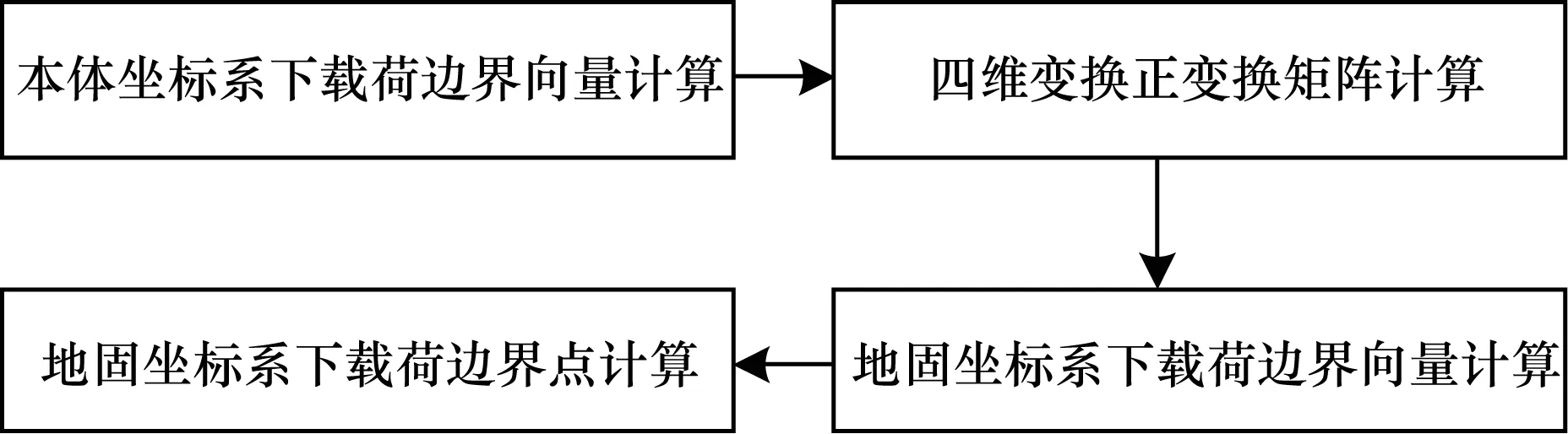
图6 基于四维转换的载荷覆盖区域计算过程Fig.6 Calculation process of load coverage area based on four-dimensional transformation

2.2.2 四维转换矩阵计算

在使用三维矩阵进行坐标变换时,由于进行位移变换时需要对三维坐标进行加操作,在进行旋转与缩放变换时需要进行乘操作[20],因此运算过程复杂,而且不利于其逆变换。本文使用四维转换矩阵对3种变换进行统一,将运算过程全部转换为乘操作,在简化坐标转换逻辑的同时实现逆变换。基本变换公式如下:

Vr=T·R·N·Vo

(1)

其中,Vo为原始四维坐标,Vr为变换后的四维坐标,T为四维位移矩阵,R为四维旋转矩阵,N为四维缩放矩阵。

对于任意的三维坐标(x,y,z),当其第4维为1时,即表示一个点,当其第4维为0时,即表示一个向量,对于任意的四维坐标(x,y,z,w),当w=0时,表示一个向量,其三维坐标为(x,y,z);当w≠0时,表示一个点,其三维坐标为(x/w,y/w,z/w)。

对于任意的平移转换(tx,ty,tz),T的四维矩阵为:

(2)

以绕x轴旋转θ角为例,R的四维矩阵为:

(3)

对于任意的缩放变换(sx,sy,sz),N的四维变换矩阵为:

(4)

四维矩阵在求逆变换时有巨大的优势,对于一个四维变换M=T·R·N,其变换矩阵为:

M=N-1·R-1·T-1

(5)

因此,当卫星在地球固定坐标系下的坐标为(x,y,z)时,卫星本体坐标系相对于地球固定坐标系旋转角度分别为θx、θy、θz,并且当载荷相对于卫星旋转角度为θr、θp、θh时,其四维转换矩阵为:

(6)

2.2.3 基于四维逆变换的过境分析计算

由于四维变换矩阵的逆变换计算简单,因此本文通过四维逆变换矩阵,将地面点坐标转换至卫星本体坐标系,并通过计算地面点与卫星本体坐标原点间的角度关系进行判断。

通过计算卫星S、地面点G与坐标原点形成角θog进行初步筛选,对于矩形载荷,θog应满足:

θog≤π/2-min(θxh,θyh)

(7)

对于圆形载荷,θog应满足:

θog≤π/2-θfov

(8)

若θog满足条件,则根据地面点在地固坐标系下的坐标(xge,yge,zge)及式(6)所计算出的四维转换矩阵M,计算地面点在卫星本体坐标系下的坐标(xgovygo,zgo):

(9)

对于矩形载荷,计算G、S与z轴所形成的角在xSz面上的投影θxSz及在ySz面上的投影θySz:

(10)

若载荷能够覆盖地面点,则:

(11)

对于圆形载荷,则直接计算G、S与z轴所形成的角:

(12)

若载荷能够覆盖地面点,则:

|θGSz|≤θfov

(13)

2.3 载荷仿真结果及过境分析结果可视化

载荷可视化主要是通过Cesium进行实现的。Cesium框架并未直接提供卫星载荷实体类,仅提供了一种柱体实体类,可以通过柱体的顶部半径设置为0使其显示成为椎体,但这一类实体无法根据实际需求任意调节载荷的视场角及三维旋转,无法直接使用。Cesium框架中包含两种图形接口,即Entity和Primitive接口,虽然都可以绘制图形,从而显示数据可视化,但相较于Entity接口,Primitive接口更加接近WebGL底层,在加载时效率更高,自由度也更高,因此,本文采用在Primitive接口基础上对其进行二次开发,对卫星载荷类进行封装。

如图7所示,卫星载荷可视化类参数主要包括6项,分别用于确定卫星载荷名称、载荷外部纹理、载荷边界宽度、载荷边界颜色、载荷边界点坐标以及载荷顶点坐标。载荷边界点坐标是通过计算服务器获取的一组边界点坐标值,在可视化过程中,每次读取坐标数组中的2个坐标,并与载荷顶点坐标一同传入 PolygonGraphics接口,形成三角形,最终通过多个三角面对卫星载荷进行可视化模拟,可视化结果如图8所示。其中,图8(a)为矩形载荷三维可视化结果,图8(b)为圆形载荷三维可视化结果,每种载荷参数在每幅图左上角均有显示,也可以通过添加动作进行实时更改。

图7 卫星载荷可视化类参数Fig.7 Parameters of satellite load visualization

图8 卫星载荷可视化结果Fig.8 Visual results of satellite load

过境分析结果主要通过图9所示界面展示给用户,用户根据分析结果确定过境时间与时长,从而对卫星或载荷下一步行动进行设置。

图9 卫星载荷过境分析的可视化结果Fig.9 Visual result of satellite load transit analysis

2.4 场景信息保存及读取

场景信息的保存与读取是仿真场景及仿真结果共享的基础。本文平台提供了本地保存及读取以及网络保存及读取2种方式。把场景基本信息保存为一个JSON文件,并将其下载到本地或上传至服务器端实现场景的保存。

如图10(a)所示,JSON文件中主要包括场景开始、结束时间以及9个不同的实体及实体参数列表,其中实体参数列表中保存了如图10(b)所示的实体主要参数及计算结果。平台通过读取JSON文件并根据实体参数对场景中的实体进行设置,从而实现场景信息的恢复。

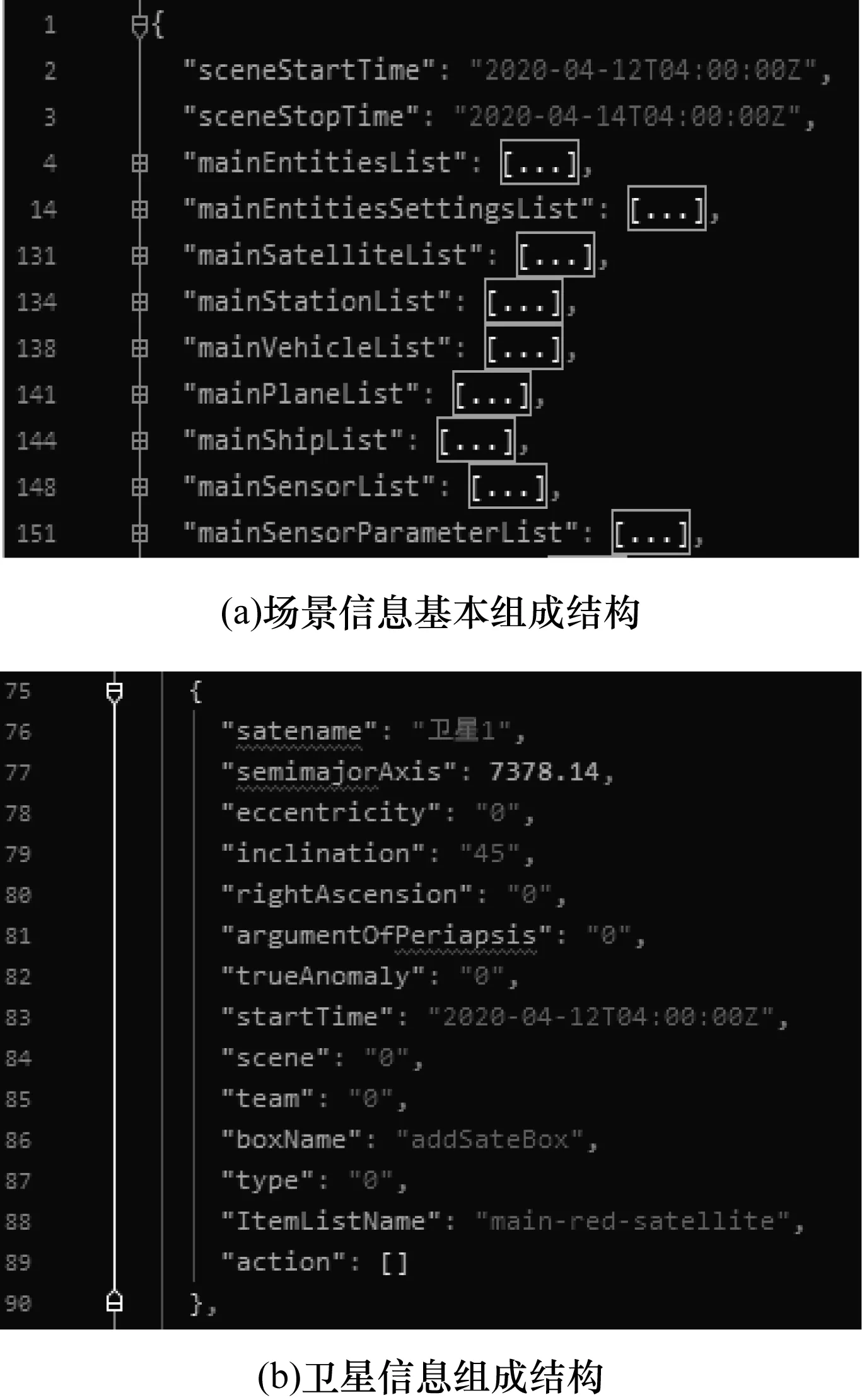
图10 场景JSON数据Fig.10 JSON data of scene

3 仿真与结果分析

为验证本文方法的有效性,针对圆形载荷和方形载荷,在不同侧摆角下对地面固定目标与对地面移动目标的覆盖情况分别进行仿真,并与STK结果进行对比。

本文实验使用的机器配置如下:操作系统Windows 10,处理器Intel Core I9-9900K,显卡NVIDIA GeForce RTX 2080 8 GB,内存DDR4 64 GB。本文平台可视化基于Cesium架构使用JS语言实现,后台计算服务器使用Nodejs实现。

仿真起始时刻为2020年4月12日04:00:00(UTCG),仿真结束时刻为2020年4月14日04:00:00(UTCG)。所使用的卫星轨道参数、载荷参数及地面目标参数如表1～表3所示。

表1 卫星轨道参数Table 1 Satellite orbit parameters

表2 载荷参数Table 2 Load parameters (°)

表3 地面目标经纬度Table 3 Latitude and longitude of ground targets (°)

3.1 载荷可视化结果

图11为卫星1搭载方形载荷情况下本文平台与STK软件的可视化结果对比。其中,图11(a)与图11(c)为STK可视化结果,图11(b)与图11(d)为本文可视化结果,图11(a)与图11(b)为2020年4月12日04:00:00(UTCG)时刻,载荷滚动角、俯仰角、偏航角均为0°情况下的对比,图11(a)与图11(b)为2020年4月12日07:33:14.950(UTCG)时刻,载荷滚动角为8°、俯仰角为16°、偏航角为40°情况下的对比。可以看出,本文平台可视化结果与STK结果基本一致,同时通过设置地面边界颜色,其使地面覆盖情况可以更清晰地展现在用户面前。

图11 矩形载荷可视化结果对比Fig.11 Comparison of visual results of rectangular load

如图12所示,本文对卫星2参数搭载圆形载荷可视化结果与STK软件可视化结果进行了对比。其中,图12(a)与图12(c)为STK可视化结果,图12(b)与图12(d)为本文平台可视化结果,图12(a)与图12(b)为2020年4月12日04:00:00(UTCG)时刻,载荷滚动角、俯仰角、偏航角均为0°情况下的对比,图12(a)与图12(b)为2020年4月13日05:04:29.436(UTCG)时刻,载荷滚动角为-4.3°、俯仰角为-8.6°、偏航角为0°情况下的对比。可以看出,本文平台可视化结果与STK结果基本一致。

图12 圆形载荷可视化结果对比Fig.12 Comparison of circular load visual results

如图13所示,本文还增加了对载荷覆盖边界的可视化仿真,用户可以根据自身需要,获取边界点及载荷中心点的具体坐标。图13(a)为圆形载荷获取边界点及载荷中心点的可视化结果,图13(b)为矩形载荷获取边界点击载荷中心点的可视化结果。通过获取载荷覆盖范围的中心点及边界点,可以更清晰地了解载荷的覆盖情况,同时也为对地面成像仿真提供了便利。

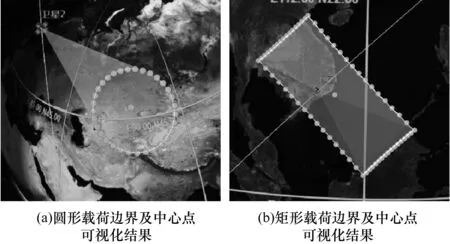
图13 载荷边界及中心点可视化结果Fig.13 Visual results of load boundary and center point

实验结果表明,本文提出的四维变换矩阵法能够通过Cesium平台对卫星载荷进行有效仿真,相较于STK,用户还可以通过交互手段,在仿真过程中实时获取载荷具体覆盖区域,并动态改变其载荷参数。同时,通过将数据计算与可视化相分离,有效减少了前台的计算压力,进一步提升了仿真的效率。

3.2 过境分析结果

表4为卫星1搭载矩形载荷在载荷无偏转情况下对固定目标的过境分析结果对比。图14(a)和图14(b)为矩形载荷在2020年4月12日07:46:31.81(UTCG)时刻STK与本文过境可视化情况对比,图14(c)和图14(d)为圆形载荷在2020年4月12日14:13:16.27(UTCG)时刻STK与本文过境可视化情况对比。可以看出,本文方法与STK结果误差极小,均在毫秒级别,同时通过图14可见本文平台计算结果与可视化结果一致。

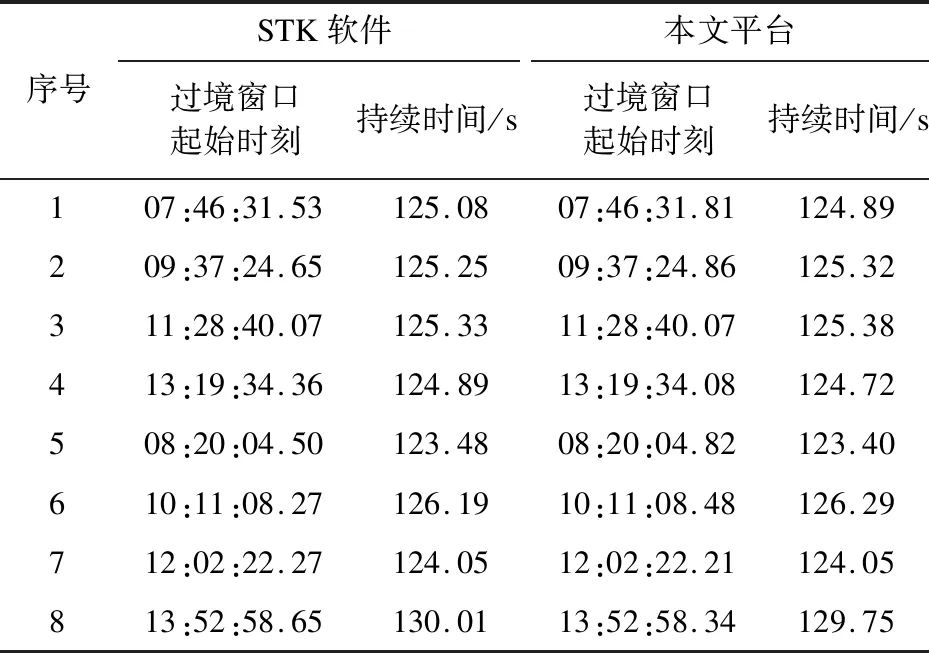
表4 过境窗口起始时刻及持续时间对比Table 4 Comparison of the start time and duration of the transit window

图14 过境开始时刻可视化结果对比Fig.14 Comparison of visual results at the beginning of transit

图15、图16分别为本文平台所计算的卫星搭载不同载荷对固定目标及移动目标的过境起始时刻及过境持续时间分析结果与STK软件计算结果之间的误差。可以看出,在载荷无偏转情况下,过境起始时刻及过境时长误差均在0.1 s左右,在载荷偏转情况下,过境起始时刻及过境时长误差均在0.5 s左右,基本可以满足工程实践中的需要。

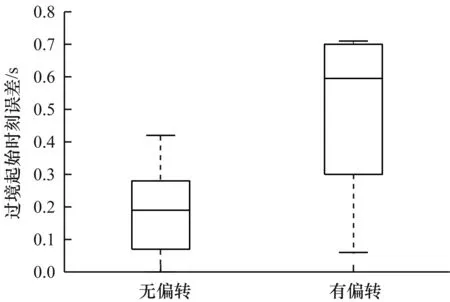
图15 过境起始时刻误差Fig.15 Transit start time error

图16 过境时长误差Fig.16 Transit time error

4 结束语

本文设计一种基于Cesium的卫星载荷可视化仿真分析平台,通过将复杂数据计算置于云端,使其能在任意浏览器上流畅运行,有效提高了可视化仿真的便捷性,同时利用JSON文件对仿真数据进行存储,降低了仿真结果共享难度。此外,还提出一种基于四维矩阵的载荷边界及过境仿真计算方法。仿真结果表明,本文方法可以得到较好的卫星载荷可视化仿真效果,准确分析过境情况。本文仅对单个目标进行分析,并只仿真了单个卫星的情况,下一步将针对区域目标进行研究,同时提高大量卫星数据的计算效率。