基于3种空间预测方法的黄土区土壤颗粒组成空间分布研究—以宁夏海原县为例

申哲，张认连，龙怀玉，王转，朱国龙，石乾雄，喻科凡，徐爱国

（1中国农业科学院农业资源与农业区划研究所，北京 100081；2北京大学地球与空间科学学院，北京100871）

0 引言

【研究意义】土壤质地是十分稳定的土壤自然属性，也是最基础的土壤物理性质之一，它影响土壤的通气透水性、保水保肥性[1]，决定着诸多其他土壤物理化学行为。黄土高原地区是我国主要的农业生产区，也是水土流失严重、生态脆弱区[2]，因此，利用空间预测方法实现对黄土区土壤颗粒组成空间分布的精准预测，了解其空间分布规律，有助于研究黄土区域土壤侵蚀和土壤化学元素行为特征，为区域农田施肥、灌水的精准化管理和土壤质量评价提供科学依据。【前人研究进展】地统计学方法是预测土壤属性空间分布最常见、最成熟的方法，以克里格插值最具代表性。传统的普通克里格（ordinary Kriging，OK）适用于较均一、土壤属性变化不强烈的环境[3-4]，在小尺度和均质景观区域应用较多[5-7]。黄土高原地形复杂，土壤属性空间变异程度大，其空间分布受地形等因素影响显著[8-9]，结合辅助变量的混合插值模型和常规统计模型在黄土区取得了较好的空间预测效果。文雯等[10]利用基于土地利用类型修正的OK对黄土丘陵区土壤有机碳进行了空间插值。连纲等[11]以地形因子和土地利用方式为辅助变量，采用多元线性回归（multiple linear regression，MLR）和回归克里格（regression Kriging，RK）对黄土高原县域土壤养分进行空间预测，结果表明RK有效地减小了预测残差，精度高于MLR。LIU等[12]利用空间状态方程和 MLR结合地形、气候等要素对整个黄土高原的土壤有机碳进行空间模拟，结果表明空间状态方程取得了更好的预测效果。除加入辅助变量提高预测精度以外，经验贝叶斯克里格（empirical Bayesian Kriging，EBK）也被证明是一种可对非均质景观区域进行空间预测的插值方法[13]，但目前该方法在黄土区应用较少。地统计和传统统计模型均难以拟合土壤属性和环境变量之间的非线性关系，且面临着处理类别型变量的困难。为克服这些局限，分类与回归树（classification and regression tree，CART）、神经网络（artificial neural network，ANN）等机器学习方法被引入到土壤属性空间预测中，研究表明这些模型能成功预测类别型变量、提高土壤属性预测的精度[14-15]，但两者均易过度拟合[16-17]，且神经网络过程繁琐。随机森林（random forest，RF）模型在分类与回归树模型基础上发展而来，具有计算简单、不易过度拟合、反映辅助变量重要程度等特点[18]，目前在平原和山区、流域等母质多样化地区应用较多。LIU等[19]基于MODIS获取的地表温度资料，用RF法完成了江苏平原土壤颗粒组成、有机质和PH的空间制图。郭澎涛等[20]利用RF结合多源环境变量（成土母质、平均降雨量、平均气温和归一化植被指数）对橡胶园土壤全氮含量进行空间预测，并与MLR、CART比较，结果表明RF模型表现最优。MAREIKE等[21]在厄尔多瓜安第斯山脉对土壤颗粒组成空间分布的研究和GERALD 等[22]在布基纳法索西南部小流域对土壤颗粒组成、有机碳空间预测的研究均表明，RF法优于其他机器学习方法。【本研究切入点】就研究对象而言，前人对黄土区土壤属性空间预测的研究集中在土壤养分指标，对土壤颗粒组成等物理属性研究相对较少。与土壤养分指标相比，土壤颗粒组成受人类活动等随机因素的影响较小，受母质、地形、气候等结构性因素影响较大，空间分布规律性更强。且土壤颗粒组成属于成分数据，预测结果要满足非负、定和为1的要求。就空间预测方法而言，目前黄土区已有的研究中对较新近的EBK使用较少，且缺乏地统计学方法与机器学习方法的对比研究。就辅助变量的选择而言，平原地区多选择高光谱数据[23-24]、地表温度[19]等作为辅助变量进行预测；山区、流域多为母质多样化地区，以地形因子结合成土母质[20,25]为辅助变量能取得理想的预测结果。但在地形复杂、母质较为单一的区域，成土母质无法作为辅助变量参与空间预测，仅使用地形因子预测可能精度并不高，需考虑加入其他环境变量提高预测精度。因此，对地形复杂、单一母质地区的土壤属性进行空间预测时，在方法的选择、辅助变量的选择方面仍需进一步研究。【拟解决的关键问题】本文选择黄土、黄土状母质的宁夏自治区海原县为研究区，选用3种方法（SLR-EBK、SLR-RK、SLR-RF）结合地形、土壤类型、归一化植被指数等辅助变量进行表层土壤颗粒组成的空间制图，并进行精度对比选出最优模型，以期为地形复杂的黄土母质区土壤颗粒组成的空间预测提供依据。

1 材料与方法

1.1 研究区概况

海原县地处黄土高原西北部（36°6′—37°4′N、105°9′—106°10′E），面积 689 900 hm2。该区属大陆季风气候，年均气温7℃，≥10℃年积温2 398℃，年平均降水量 363 mm，降水量由南向北递减。县内地势由西南向东北倾斜（图1），地貌以黄土丘陵为主，南部月亮山、中部南华山、西部西华山、北部油井山呈孤立零星分布，被黄土丘陵包围，东北角与同心县交界处为狭长的河谷冲积平原，面积较小，为提灌区。研究区内绝大部分成土母质为黄土、黄土状母质，仅在南华山、西华山零星分布有岩石风化物。土壤类型包括灰褐土、黑垆土、黄绵土、灰钙土、新积土、红黏土和粗骨土7种，各土壤类型面积占比见表1。其中黄绵土、黑垆土、灰钙土 3个土类面积最大，共占全县面积的81.51%。以盐池乡-李旺一线为界，此线以北主要为灰钙土，以南黄绵土和黑垆土插花分布，南华山、西华山发育有灰褐土，丘陵间低地及冲积平原有新积土分布。海原县以雨养农业为主，土地利用类型主要为旱地、草地，种植作物主要为玉米、荞麦、马铃薯。

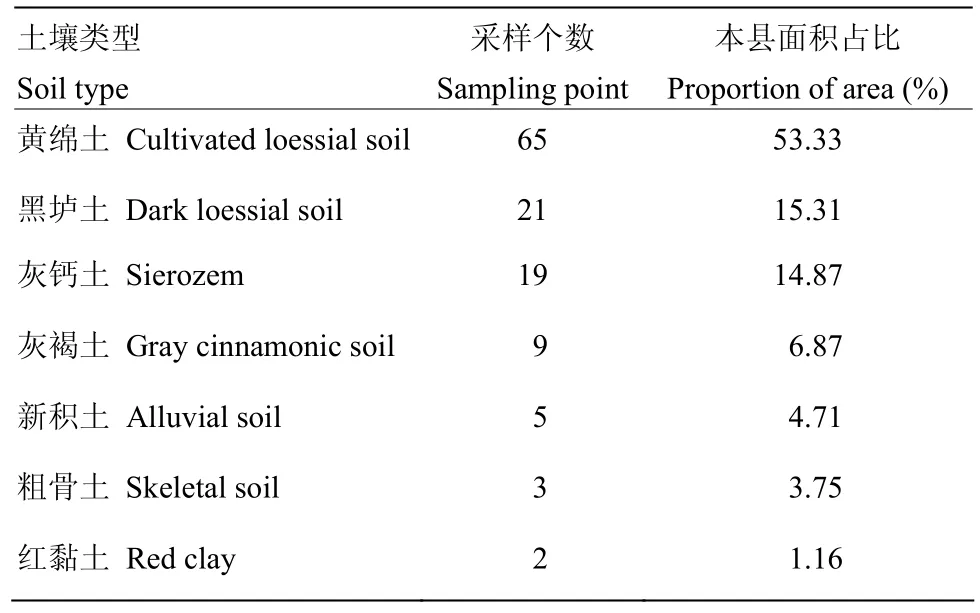
表1 各土壤类型面积占比及样点统计Table 1 The area proportion and sample points of each soil type

图1 研究区位置及样点分布图Fig. 1 The map of the study position and sampling sites

1.2 样品采集与分析

采用网格法布点，在此基础上综合考虑地形地貌、土壤类型等因素，在南华山、西华山等地形复杂地区加密样点，共选取具有代表性的样点124个（图1）。以盐池乡-南华山-九彩乡一线为界，南部面积占32%，采样点共53个，占全部采样点的43%，平均每4 300 hm2一个样点；北部面积占68%，采样点共71个，平均每6 600 hm2一个样点。研究区全部样点平均间隔7—8 km。东南部边缘因地势陡峭无路，取样较困难，故3个样点取在海原县外3—5 km范围内。各土壤类型的采样点个数见表1。土壤样品采集时间为2018年9月、2019年4月，采样深度为0—20 cm，记录样点经纬度、地形地貌、土壤类型、土地利用类型等信息。土壤颗粒组成采用湿筛-吸管法测定[26]，粒级划分采用国际制（砂粒2—0.02 mm，粉粒0.02—0.002 mm，黏粒＜0.002 mm）。

1.3 辅助变量来源及处理

海原县内地形复杂，地势起伏较大，海拔落差大于1 600 m，地貌类型主要包括山地、黄土丘陵、平原。因地形地貌不同，各区域温度、降水量、植被差异较大，直接影响成土过程，进而影响土壤颗粒组成的空间分布。土壤类型是五大成土因素综合作用的产物，一定程度上包含土壤质地的信息；土壤类型也含有母质信息，而本研究区母质相对单一，因此，其他因素对质地的影响会更大；另外，许多研究表明，土壤类型与土壤有机质、容重有一定相关性[27-28]。温度、降水量对土壤颗粒组成有影响，由于缺乏研究区较精细的温度、降水数据，而植被覆盖情况直接受温度、降水影响，且研究区基本为雨养农业，故将反映植被覆盖程度的归一化植被指数作为辅助变量反映气候因素。同时地形、土壤类型在一定程度上也包含气象信息。与土壤养分相比，土壤颗粒组成稳定，受人为耕作影响较小，研究区土地利用类型主要为旱地和草地，受灌水耕作影响很小，因此本研究区黏土矿物分解更加缓慢。综上所述，本研究选取的辅助变量为地形因子、土壤类型、归一化植被指数。

1.3.1 辅助变量来源

（1）宁夏自治区1∶50 000等高线矢量图；（2）宁夏自治区1∶200 000土壤图；（3）本文使用处于植物生长季（8—9 月）、且云量覆盖度少（小于5%）的卫星影像计算植被指数。2017年8月28日和9月6日的Landsat8 OLI_TIRS 四景卫星影像覆盖海原县全境，影像均来源于地理空间数据云网站（http://www.gscloud.cn）。由于缺乏研究区2018年5月以后的卫星影像，故采用前一年相应月份的影像代替。

1.3.2 辅助变量的提取及处理

（1）用 1∶50 000等高线矢量图在 ArcGIS10.2中生成10 m分辨率的数字高程模型（digital elevation model，DEM）栅格影像，从中提取 5个地形因子：高程（elevation，Ele）、坡度（slope，Slo）、平面曲率（horizontal curvature，HC）、剖面曲率（profile curvature，PC）、地形湿度指数（topographic wetness index，TWI）。使用SAGA GIS软件基于DEM提取风力作用指数（wind exposition index，WEI）[29]，该指数是各个风向对区域的风影响（wind effect）[29]的平均值。WEI越大，表明该区域越容易受风力影响。（2）土壤类型（soil types，ST）为类别变量，本文采用“算术平均值变换”[30]，以不同土壤类型下定量因变量的算术平均值代替该土壤类型，即将土壤类型变为一个具有7个数值的定量变量。由于有砂粒、粉粒、黏粒3个因变量，则土壤类型共转化为3组定量变量，分别用于构建砂粒、粉粒、黏粒的预测模型。算术平均值变换用动态思维（类别自变量与定量因变量的关系）建立起自变量各水平与定量结果变量之间数量关系，比传统的哑变量变换更具合理性[30]；此外，哑变量变换将具有n个水平的类别变量变为（n-1）个二值变量，这些二值变量非相互独立[31]，需全部进入回归模型中，造成模型中无关变量太多，拟合精度不高，而算术均值变换将类别变量变为具有n个数值的定量变量，提高了回归拟合精度[30]。（3）在ENVI5.1中对遥感影像进行镶嵌、计算，提取归一化植被指数（normalized difference vegetation index，NDVI）。（4）为消除变量之间的量纲影响，对变量进行归一化处理。

1.4 预测方法

1.4.1 数据转换方法 为了使数据满足正态分布，且使预测结果满足非负、定和为1的要求，本文首先对土壤颗粒组成进行对称对数比（symmetry log-ratio，SLR）转换[32]，转换公式为：

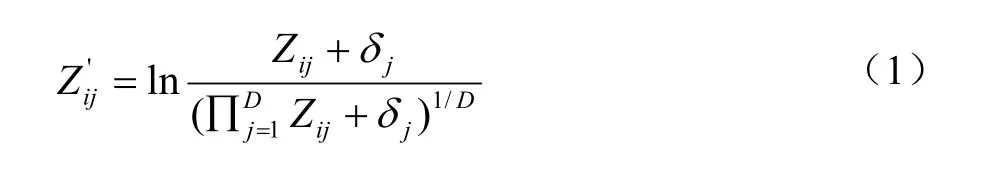
转回公式为：

式中，Zij代表第i个样点第j种粒级的相对含量（%）；代表第i个样点第j种粒级含量的转换值；D表示成分数据的维度，本文中D=3；δj为常数，取研究区第j种颗粒除0外最小含量的一半。

1.4.2 经验贝叶斯克里格（EBK） EBK在OK的基础上发展而来，可以通过构造子集、建立局部模型对非平稳数据进行空间插值[33]。它克服了OK的两大局限：第一，EBK则通过构造子集，通过评估较小子集上的半方差函数，在研究区的不同区域中得到不同的半方差函数模型，克服了OK假设单一半方差函数可准确表示所有位置数据的空间结构的局限。第二，在半方差函数的参数评估方面，OK只依赖于单一半方差函数，忽略了模型的不确定性[34]，因此在构建半方差函数的过程中，需对每个参数进行手动反复调试，以使该模型更接近于真实的半方差函数。而EBK在每个子集中，自动评估半方差函数，并以此半方差函数来模拟子集中的新数据值。然后使用这些模拟的数据值来评估子集的新半方差函数。此模拟和评估过程重复多次，并且在每个子集中生成多个模拟的半方差函数，最后将这些模拟混合在一起以生成最终的预测图。本研究中，训练集砂粒、粉粒、黏粒含量经SLR转换后的全局Moran’s I（莫兰指数）分别为0.293、0.260、0.192，且P值均小于0.05，表明经SLR转换的土壤颗粒组成在研究区域内有一定的空间自相关性。ArcGIS趋势分析发现，转换后的砂粒、粉粒含量均存在二阶趋势，不满足空间平稳假设。Voronoi图也显示两者的局部空间规律变化较大，因此使用EBK进行空间插值。具体步骤为：（1）将数据分为多个特定大小的重叠子集（通过逐次尝试，最终本文每个子集设置为70个点，子集重叠系数设置为3，即每个点可落入3个子集中）；（2）对子集中的数据进行半方差函数拟合；（3）使用该半方差函数，在每个输入位置生成新值；（4）使用新的模拟数据生成新的半方差函数；（5）将步骤（3）和（4）重复100次。此过程将为每个子集生成100个半方差函数，每个都是子集真实半方差函数的估计。将其绘制在一起生成按密度着色的半方差函数分布；（6）对于空间内每个位置，都使用唯一的半方差函数分布生成预测，该分布是通过周围子集的半方差函数分布加权综合计算得出的；子集距离预测位置越近，给定的权重就越高。这就保证了每个预测值使用的是临近数据所定义的模型，而不是远处数据所定义的模型[13]。最后，将局部预测结果混合生成全局预测结果。

1.4.3 回归克里格（RK） RK是应用多元线性回归拟合土壤属性与辅助变量间的关系，然后对回归残差应用克里格法插值，最后将回归预测结果与残差插值结果结合起来的一种空间预测方法。首先用皮尔森相关分析对辅助变量进行初步筛选，表2相关分析的结果表明，高程、归一化植被指数和土壤类型与土壤颗粒组成显著相关。其中，高程和NDVI均与土壤砂粒含量呈负相关，与粉粒和黏粒含量呈正相关。为避免辅助变量间的共线性问题，基于筛选出的变量，采用逐步线性回归的方法对经 SLR转换后的土壤颗粒组成进行预测（F值的概率Fp＜0.05为变量进入方程的标准，Fp＞0.10为剔除变量的标准），并对预测残差进行简单克里格插值，最后将回归预测值与残差相加并转回得到预测结果。

表2 土壤各粒级含量与辅助变量的相关性分析Table 2 Pearson correlation coefficients between soil particle size distribution and auxiliary variables

1.4.4 随机森林（RF） 与其他模型一样，随机森林（RF）可以反映若干自变量对因变量的作用[35]。其主要过程包括：从原始训练集中进行bootstrap重新抽样（有放回的随机抽取）构成新的训练集生成决策树；同时，随机地选择部分变量进行决策树节点的确定；随机地生成几百至几千个决策树构成随机森林。对于分类问题，所有决策树预测结果中得票最高的分类结果为最终结果；对于回归问题，所有决策树预测结果的平均值为最终的预测结果[18]。每次未被抽到的样本组成袋外样本，故RF可根据袋外误差估计模型误差，对于分类问题，袋外误差是分类错误率；对于回归问题，袋外误差通过回归残差计算，本文采用均方误差（mean square eroor，MSE）。

RF不要求原始数据符合正态分布，但为了更好地同其他两种方法做对比，且使预测结果满足定和为 1的要求，本研究使用经SLR转换后的数据进行建模。由于 RF不是简单的线性回归，皮尔森相关分析筛选变量的结果不一定适合 RF模型，故用两步法对 RF辅助变量进行筛选：对变量进行重要性排序，初步剔除不重要变量[36]；对剩下的变量，基于随机森林逐步选择[37]。本文采用Breiman经典随机森林版本中的评价方法，通过变量值的置换计算变量重要性得分，剔除得分小于0的变量。结果表明平面曲率、剖面曲率两个辅助变量重要性得分均小于 0，故剔除。剩下的变量按照重要性评分降序排列，以不同的变量子集所构建森林运行100次的MSE均值作为逐步筛选变量的标准，从最重要变量开始，遍历所有变量，MSE最小结束（变量筛选过程中，RF参数均为默认参数）。基于筛选的辅助变量对 RF模型进行参数优化：首先以 MSE最小化为目标，通过逐次计算确定决策树节点分裂时所用变量个数（mtry）；通过观察决策树数量（ntree）与误差关系图，在保证误差稳定的前提下，选择较小的ntree[38]。

本研究中随机森林在R3.5.2中完成，相关性分析和逐步回归使用SPSS 22软件，经验贝叶斯克里格插值、回归残差的简单克里格插值和空间制图在ArcGIS 10.2中完成。

1.5 精度验证

从124个样点中随机选取80%的（100个）样点用于空间预测，20%的（24个）样点用于精度验证[39-40]，训练样点和验证样点的分布如图1所示。本研究采用验证集的平均绝对误差（MAE）、均方根预测误差（RMSE）、平均Aitchison距离（MAD）[41]进行模型精度评价。MAE能更好地反映预测值误差的实际情况；RMSE对系统误差和随机误差都很敏感，常用来评估不同模型的预测精度；MAD可以反映成分数据预测值和观测值之间整体的相似性。MAE、 RMSE、MAD越小，模型精度越高。

Zij代表第i个样点第j种粒级含量的观测值；代表第i个样点第j种粒级含量的预测值；n表示验证点的数量；D表示成分数据的维度，本文中D=3。

2 结果

2.1 土壤颗粒组成的描述性统计特征

表3为研究区采样点土壤颗粒组成的描述性统计结果，可以看出研究区土壤砂粒含量最高（训练集和验证集砂粒平均含量分别为61.82%、63.96%），黏粒含量最低（训练集和验证集的平均黏粒含量分别为14.56%、13.36%），粉粒含量居中（训练集和验证集的平均粉粒含量分别为23.62%、22.68%）。训练集中3个粒级含量的范围和标准差都比验证集中的大，相对应地，训练集中砂粒、粉粒、黏粒含量的变异系数（14.02%、23.96%、27.41%）大于验证集（11.30%、21.91%、25.45%）。方差分析结果表明训练集与验证集土壤3个粒级含量差异均不显著，表明训练数据和验证数据都具有较好的代表性。训练集中3个粒级含量偏度均接近于0，但经Kolmogorov-Smirnov检验，只有砂粒含量P值大于0.05，满足正态分布，粉粒和黏粒含量均不符合正态分布。经SLR转换后，砂粒、粉粒、黏粒含量均符合正态分布，可用于空间插值和线性回归。

2.2 多元线性回归和RF模型的构建

由表4可以看出，最终进入土壤颗粒组成线性回归预测模型的辅助变量包括高程 Ele和土壤类型，NDVI由于与高程、土壤类型存在多重共线性，在逐步线性回归的过程中被剔除。从调整决定系数（AdjustedR2）来看，砂粒含量的线性回归模型方差解释率最高（0.339），拟合度较好；粉粒和黏粒含量的线性回归方程方差解释率较低（分别为 0.208，0.205），拟合度较差。表5为RF模型的拟合结果，可以看出进入模型预测的辅助变量除了高程 Ele、土壤类型外，还包括坡度Slo和风力作用指数WEI，这主要是因为 RF可以拟合土壤颗粒组成和辅助变量之间的非线性关系。其中，高程对3个粒级含量的空间预测来说，均是最重要的辅助变量，其次是土壤类型，坡度、风力作用指数的重要性相对较低。虽然 RF对辅助变量间的多重共线性不敏感，但考虑到NDVI对预测精度无显著影响，为了简化模型，提高计算速度，本研究未将NDVI作为RF的辅助变量。

表3 研究区采样点土壤颗粒组成基本统计特征Table 3 Statistical characters of soil particle size distribution in study area

表4 土壤颗粒组成逐步线性回归方程拟合结果Table 4 Fitting of soil particle size distribution with the stepwise linear regression equation

表5 SLR-RF参数拟合结果Table 5 SLR-RF parameter fitting results

2.3 土壤颗粒组成的空间分布预测结果

利用拟合的SLR-EBK、SLR-RK和RF模型分别对研究区土壤砂粒、粉粒、黏粒含量的空间分布进行预测，得到其空间分布图（图2—4）。可以看出，3种方法预测的土壤各粒级含量空间分布的趋势大体一致。研究区砂粒含量基本呈现西南部低，东北部高的趋势，其中西华山-南华山-九彩乡海拔较高一带含量较低，集中在60%以下，北部和东部边缘含量较高，大多数为65%—70%，部分达到70%以上。粉粒和黏粒含量的空间分布趋势与砂粒相反，呈现西南部高，东北部低的趋势，西华山-南华山-九彩乡一带粉粒含量变化范围集中在 25%—30%，黏粒含量变化范围集中在 15%—20%，北部和东部边缘粉粒含量低至 20%以下，黏粒含量大部分为10%—15%。土壤颗粒组成的空间分布趋势明显受到海拔的影响。

虽然3种方法预测的土壤颗粒组成空间分布总体趋势比较相似，但在局部区域上不尽相同。首先，SLR-RK和SLR-RF的预测结果对细节刻画比较清晰，而 SLR-EBK预测结果只能反映海原县土壤颗粒组成的宏观分布趋势，难以体现局部变异信息。其次，虽然3种方法预测的砂粒、粉粒、黏粒含量的平均值相近（SLR-EBK、SLR-RK、SLR-RF 3种方法预测砂粒含量的均值分别为62.32%、62.83%、62.53%，粉粒含量的均值分别为23.34%、23.25%、23.38%，黏粒含量的均值分别为14.34%、13.91%、14.09%），但由图2—4可以看出，SLR-EBK存在平滑效应，与土壤采样点原始数据相比，该方法预测的极大值和极小值均向均值方向靠拢，SLR-RK与SLR-RF的预测范围更接近实测值。

图2 SLR-EBK预测土壤颗粒组成空间分布图Fig. 2 Spatial distribution of soil particle size distribution predicted by SLR-EBK

图3 SLR-RK预测土壤颗粒组成空间分布图Fig. 3 Spatial distribution of soil particle size distribution predicted by SLR-RK

图4 SLR-RF预测土壤颗粒组成空间分布图Fig. 4 Spatial distribution of soil particle size distribution predicted by SLR-RF

2.4 不同预测方法的精度对比

表6列出了3种方法在验证集的预测精度，可以看出SLR-RF法对3个粒级含量预测的MAE和RMSE均低于其他两种方法，且SLR-RF的MAD（0.208）最低，表明该方法的预测精度更高。因此，研究区土壤颗粒组成的最优预测模型为SLR-RF。

表6 不同空间预测方法精度对比Table 6 Accuracy comparison of different spatial prediction methods

3 讨论

3.1 3种预测方法的精度

本文利用3种方法在宁夏南部黄土丘陵区对土壤颗粒组成的空间分布进行预测，结果显示，SLR-EBK方法预测精度较低，原因在于空间插值方法仅利用了土壤颗粒组成的空间自相关性，忽略了环境变量的影响。虽然EBK在一定程度上考虑了土壤属性变化的不均匀性，但由于本研究区地形破碎，且南部高山区与北部黄土丘陵区气候条件差异大，故 SLR-EBK法预测精度并不高。

SLR-RK、SLR-RF法由于引入辅助变量参与预测，提高了土壤颗粒组成的空间预测精度，相比SLR-RK，SLR-RF的预测精度更高。可以看出，虽然RK通过对回归残差进行简单克里格插值进一步提高了多元线性回归的预测精度，但 RF通过精确捕捉土壤属性同辅助变量之间的非线性关系，依然取得了比RK更好的预测效果。在黄土母质区，地形是影响土壤属性的主要因素，精确拟合地形因子与土壤属性之间的关系是进行土壤属性空间预测的关键所在。小尺度下，气候、植被等环境条件相对一致，地形因子与土壤属性之间的关系较为简单，可直接利用线性回归拟合[20]。王库[42]以高程、坡度等为辅助变量，使用RK对福建省旗山北麓一块面积为29 000 hm2的区域进行土壤全氮的空间预测，结果表明，RK取得了较高的预测精度，验证集的决定系数达到0.682。MOORE等[43]在科罗拉多州一块 5.4 hm2的坡面上，利用多元线性回归结合地形因子（坡度、坡向、平面曲率、剖面曲率、地形湿度指数等）对土壤属性（有机质、pH、砂粒含量、粉粒含量等）进行空间预测，取得了理想的预测结果。但在大尺度区域，随着地形的变化，气候、植被等也出现明显变化，土壤属性与地形因子之间往往表现出非线性的特征，这时运用 RF进行空间预测就有明显优势。姜赛平[28]等以整个海南岛（3.29×106hm2）为研究区域，利用RK、RF结合辅助变量预测全岛的有机质空间分布，结果表明 RF预测精度高于 RK，更适合地形复杂的大尺度地区土壤属性的空间预测。本研究区面积达689 900 hm2，南北部地形、气候、植被差异较大，部分地形因子（坡度、风力作用指数）与土壤颗粒组成无显著的线性关系，并未进入回归方程，但却进入 RF模型参与空间预测，表明RF模型可以拟合土壤属性同环境变量之间的非线性关系，进一步提高预测精度。除地形因子外，本研究中土壤类型也是预测土壤颗粒组成的重要变量。土壤类型属于类别变量，与多元线性回归模型相比，RF对类别变量具有更好的包容性[44]，可以更多地捕捉土壤颗粒组成与土壤类型之间的关系。综上所述，RF更适合用于预测研究区土壤颗粒组成的空间分布。

3.2 土壤颗粒组成空间分布与辅助变量的关系

地形作为五大成土因素之一，通过影响物质与能量的再分配，引起土壤的理化性质变化[45]。本研究中，高程是预测土壤颗粒组成最重要的地形因子。皮尔森相关分析和空间预测结果均表明，海拔高度越高，砂粒含量越低，粉粒和黏粒含量越高。这与部分学者[46-48]低海拔地区土壤黏粒含量更高的研究结果不符。但也有学者与本文研究结果相似，BACIS等[49]在巴西杰尼罗州的研究表明高程与土壤质地的变异密切相关，海拔越高，黏粒含量越高。这是因为前者[46-48]的研究中，海拔主要影响土壤颗粒的运移速度和方向，粒径较小的颗粒在重力和地表径流的作用下运移的距离更远。BACIS等[49]的研究中，与海拔密切相关的是土壤母质，该地区高海拔区域土壤主要由前寒武纪片麻岩原位风化形成，质地较细；低海拔区域以砂质坡积物为主，砂粒含量较高。本研究中，海拔主要影响区域降水、植被等，研究区内区域降水量差异大，以盐池乡-李旺一线为界，南部高海拔地区降水在400 mm以上，植被覆盖度高，湿润的条件有利于黏土矿物的形成；北部低海拔地区降水为200—350 mm，植被覆盖度低，地表裸露多，蒸发强烈，土壤颗粒较粗。这也与NDVI和砂粒含量呈显著负相关，和粉粒和黏粒含量呈正相关的结果相一致。除高程外，坡度、风力作用指数两个地形因子也进入RF模型（表5），但重要性相对较低，表明这两个辅助变量虽然也会影响土壤颗粒组成的空间分布，但影响程度较小。坡度通过影响表层土壤颗粒运动、径流挟沙能力和侵蚀方式[50-51]，从而影响土壤颗粒组成。邹心雨等[52]等研究表明，坡度对小尺度下土壤颗粒组成的空间变异影响较大，本文研究尺度较大，坡度的影响并不显著。

除地形因子外，土壤类型也是预测土壤颗粒组成的重要变量。土壤类型在一定程度上可以反映母质、气候等信息，杨艳丽等[53]研究表明，土壤类型与黏粒含量的空间分布显著相关。海原县绝大部分区域为黄土、黄土状母质，在此母质上发育有黄绵土、灰钙土和黑垆土，与黄绵土和灰钙土相比，黑垆土形成的环境条件更为湿润，黏粒含量更高。海拔2 100 m以上的南华山、西华山中上部分布有页岩、泥岩和片岩的风化物，这些岩石风化物是形成山地灰褐土的主要母质，其中页岩、泥岩属于沉积岩中的泥质岩类，发育形成的土壤颗粒较细。新积土、粗骨土和红黏土的面积较小，其中新积土是在水力或重力迁移堆积的物质上形成，主要分布于东北角的冲积平原，颗粒较细；粗骨土仅分布于西华山等山地的陡坡，含较多的砂岩风化碎屑，植被覆盖度很低，土壤颗粒较粗。红黏土主要分布于研究区东南角，为裸露的第三纪红土层，质地较黏重。

本研究区地形复杂，地形因子是重要的辅助变量；区内土地利用类型多为天然草地和旱地，且单季种植，土壤物理性状受人为影响不强烈。因此要对平原地区、受人类活动影响强烈的地区进行颗粒组成的空间预测，仍需探索选取适当的辅助变量和预测方法。

4 结论

3种方法（SLR-EBK、SLR-RK和SLR-RF）预测的海原县土壤各粒级含量空间分布的趋势基本一致，表现为砂粒含量西南部低，东北部高，粉粒、黏粒则相反； SLR-RF、SLR-RK预测精度均高于SLR-EBK，其中以SLR-RF预测精度最高，为预测海原县土壤颗粒组成空间分布的最优方法；在黄土母质区，高程、土壤类型是与土壤颗粒组成的空间变异相关性较强的辅助变量。