身份基矩阵层级全同态加密方案*

陈 虹，黄 洁，陈红霖，王闰婷，肖成龙，郭鹏飞，金海波

辽宁工程技术大学软件学院，辽宁葫芦岛 125105

1 引言

格密码学的兴起归功于Ajtai[1]，1996年，他证明了格上的困难问题具有最糟糕困难安全性，这一理论说明了格在平均情况困难问题方案的安全性可以由最坏情况问题的安全性来保障。1997年，Ajtai和Dwork[2]首次提出了基于格上最近向量问题（closest vector problem，CVP）的加密方案，此后基于格的密码体制相继出现。

初期的格密码方案存在密钥尺寸过大、缺乏严格的安全性证明等缺陷，无法满足实际应用的需求。直到2005年，Regev[3]提出了基于LWE（learning with errors）困难问题的单比特公钥密码算法，大幅缩小了密文和密钥的尺寸，同时将安全性规约到格上最坏情况困难问题的难解性——在量子规约下与最坏条件下的最短向量问题（shortest vector problem，SVP）的变体一样困难。2008年，Gentry等人[4]调换了Regev方案中密钥生成算法与加密算法，提出了Regev方案的对偶加密方案。单比特加密会浪费过多的存储空间，为此Kawachi等人[5]、Peikert等人[6]相继对Regev的方案进行改进，提出了多比特加密方案。2017年，Li等人[7]提出了消息空间为的多比特加密方案。2019年，李明祥等人[8]利用Peikert等人的密文包装技术，设计了基于LWE的矩阵加密方案与身份矩阵加密方案，其消息空间为。全同态加密（fully homomorphic encryption，FHE）是指对加密后的数据进行加法或乘法运算后解密，其结果与直接对明文进行相同运算的结果相同的加密方案。随着云计算的高速发展，如何保证用户隐私数据的安全性成为了关键问题之一。全同态加密是云上用户数据安全性问题的有效解决方案。如图1所示，在应用了全同态加密方案的云计算环境下，云服务器只保存、处理用户的密文数据，并将运算结果以密文形式反馈给用户，由用户自行解密。由于在云端数据一直以密文方式存储，即便是服务器的管理人员也无法轻易窃取用户数据。也就是说，除数据拥有着自身外，其他人对该密文具有相等的破解难度。因此通过全同态加密技术，用户可以放心地将数据交给云服务器处理，而不必担心个人隐私数据泄露，有着重要的应用价值。

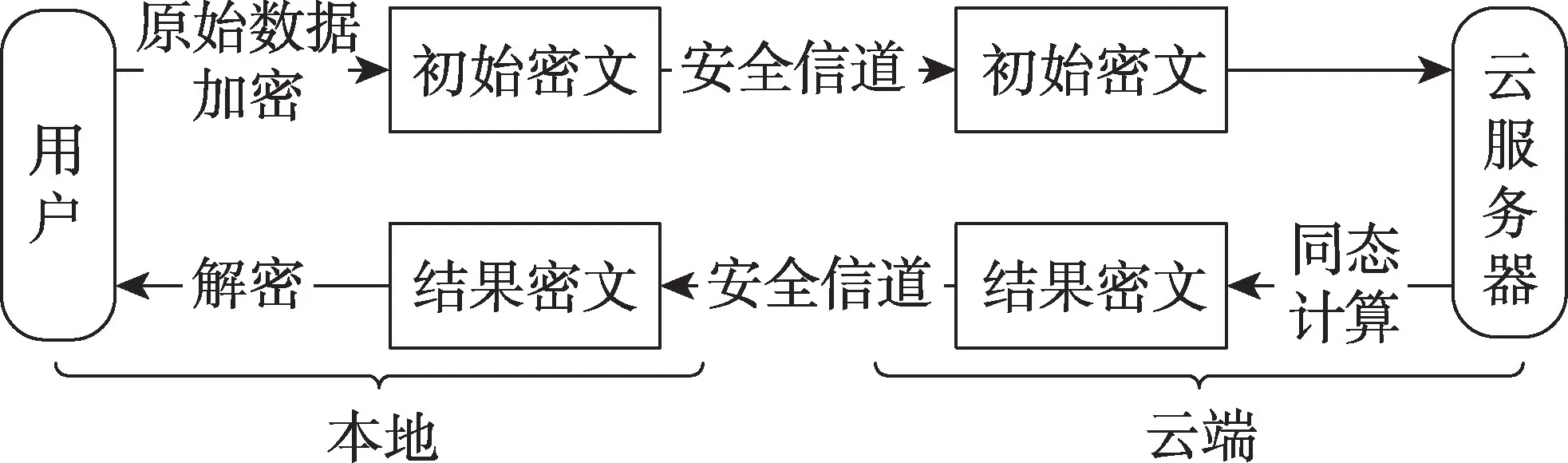
Fig.1 Working model of fully homomorphic encryption scheme图1 全同态加密方案工作模型

基于格的全同态加密研究兴起于2009年，Gentry等人[4]首先提出了基于理想格的全同态加密方案，并构建了全同态方案的构架，即先构造一个只能执行少量次数的部分同态加密方案，然后“压缩”解密电路，最后利用Bootstrapping技术实现全同态加密。基于这一蓝图，提出了许多全同态加密方案[9-10]，但Bootstrapping过程要消耗大量计算资源，因此方案效率并不高。在2012年，Brakerski等人[11]提出了不需要Bootstrapping技术的加密方案，他们利用密钥转换技术和模转换技术对密文降维、降噪，得到了可以实现多项式级同态计算的层级全同态加密方案。这一方案摆脱了复杂的Bootstrapping过程，计算效率更高。并且进行多项式级别深度的全同态运算，足够满足实际应用的需要。本文将采用Brakerski等人的思路，构造一个层级全同态加密方案。

基于身份的加密方案，简化了用户公钥的管理，常应用于资源有限的环境中。近年来，基于身份的全同态加密方案成为研究热点[12-14]，但它们都是针对单比特的全同态加密方案，无法快速处理大量的数据，特别是在对图片、视频等数据进行加密时，由于一次计算只能处理一个比特的数据，时间成本很高。而基于矩阵的全同态加密算法，每次计算都能加密一个明文矩阵，通过将图片、视频等数据矩阵化，能一次性加密大量数据，大大减少了加密耗时。2015年，Hiromasa等人[15]提出了第一个基于矩阵全同态加密方案，方案支持矩阵加法和矩阵乘法的同态操作。2018年，Wang等人[16]针对Hiromasa的方案提出改进，将密文矩阵由(减小到r×(n+r)。本文优化了文献[8]的矩阵加密方案，得到一个身份基矩阵加密方案（identity-based encryption，IBE），改进方案的明文空间为{0,1}l×l，但允许的噪声上限更小。然后基于Wang的矩阵全同态加密方案，优化了其中的密钥转换过程，使得对任意维度的公钥矩阵均能实现转换，最终得到一个基于身份的矩阵层级全同态加密方案（identity-based fully homomorphic encryption，IBFHE）。方案能同时加密l2个比特的明文，并支持矩阵同态加法、同态乘法以及同态哈达玛积运算，同时减小了噪声增长速度。

2 相关理论

2.1 符号说明

记实数集为R，自然数集为N，整数集为Z 。对任意的整数q，Zq为模q整数环，其取值范围为。对一个正整数n，[n]表示{1,2,…,n}。lb(∙)表示以2为底的对数，「·⏋、⎿·」、「·」分别表示向上取整、向下取整以及四舍五入运算。

本文中向量以小写的加粗字母表示，如u，其第i个元素表示为ui。矩阵以大写的加粗字母表示，如A，矩阵内的元素用其对应的小写字母表示，如aij。用(∙)T表示矩阵的转置。对矩阵A=(a1,a2,…,an)，其p阶范数，并记。On×m表示n×m维的零矩阵，表示矩阵X、Y的垂直连接，(X|Y)表示水平连接。记矩阵的乘法为A∙B，记矩阵的哈达玛积为A∘B。

用negl(n)表示可忽略函数，对于一个随机分布{Xn}n∈N，如果满足，则称该分布为B-有界分布。

2.2 格理论

定义1（格）设B={B1,B2,…,Bm}∈Rn×m为一组线性无关的向量，由B构成的格Λ(B)定义为这些线性无关向量的整系数线性组合。即：

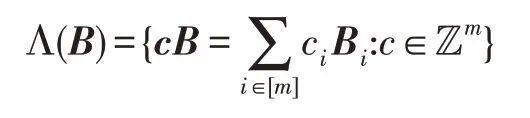
其中，B为格Λ(B)的一组基。

定义2（满秩整数格）对向量和矩阵A∈，满秩整数格定义为：

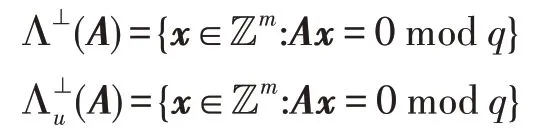
定义3（离散高斯分布）假设L为一个m维格，对任意向量c∈Rm和σ∈R＞0，有以下定义：

ρσ,c(x)=表示Rm上以c为中心，参数为σ的离散高斯分布。

ρσ,c(L)=∑x∈L ρσ,c(x)表示格L上各分量的离散高斯分布的和。

DL,σ,c表示格L上以c为中心，参数为σ的离散高斯分布。

引理1[17]对固定常数δ，存在一个概率多项式时间算法GenBasis(1n,1m,q)，对poly(n)有界的m≥δnlbq，算法输出，满足：

（1）A在统计上接近均匀分布；

（2）S是Λ⊥(A)的一组基，并且

引理2[9,14]设矩阵TA为Λ⊥(A)的基，则存在一个概率多项式时间算法SampleLeft(A,B,TA,U,σ)，输入以及高斯参数算法输出矩阵，且Wi的分布统计接近，其中F=(A|B)。

2.3 LWE

LWE实例：对安全参数λ，令n=n(λ)表示维度，整数q=q(λ)≥2，向量，X=X(λ)为Z上的噪声分布。均匀随机选择和噪声向量ei←X 。计算bi=ais+ei，输出。LWE困难问题包含以下两种形式：

定义4（LWE搜索问题）给定m个相互独立的(ai,bi)，要求解出秘密向量s，记为search-LWEn,m,q,X。

定义5（LWE判断问题）LWE的判断问题是以不可忽略的概率区分以下两个集合：第一个集合里的元素均由LWE实例产生；第二个集合由m个×Zq上的一致均匀抽样元素构成，记为DLWEn,m,q,X。

在基于LWE的密码方案中，大多是基于LWE判断问题的。文献[18-19]说明了格上近似最短向量问题可以规约到DLWEn,m,q,X上，即若能解决LWE判断问题，就能解决近似最短向量问题。具体定理如下：

定理1[18-19]令q=q(n)∈N且，其中qi两两互素，存在一个B-有界分布X满足，如果存在一个有效算法能解决LWEn,q,X问题，那么：

（1）存在一个有效的量子算法，能解决任意n维格上的判定性近似最短向量问题和近似最短独立向量问题

2.4 矩阵运算

（1）直积以及其变体：对两个矩阵A∈Zm×n和B∈Zs×t，直积(A⊗B)和其变体(A⊗′B)分别表示如下：

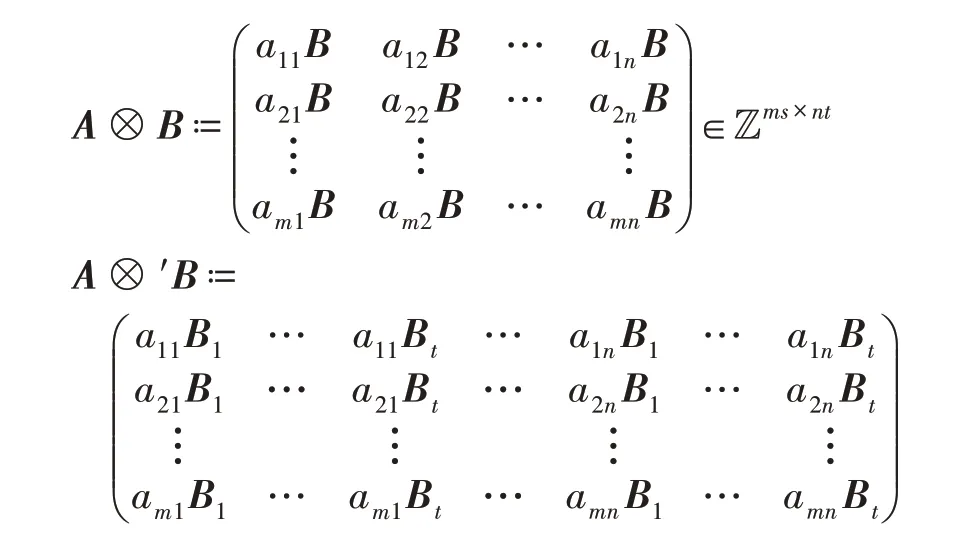
其中，Bi表示矩阵B的第i列。

定理2[16]对任意矩阵A、B∈Zm×n以及S∈Zn×m，以下等式恒成立：

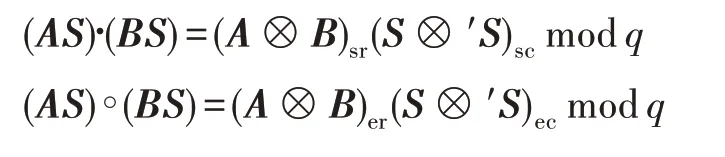
3 身份基矩阵加密方案

身份基加密方案由IBE.Setup()、IBE.Extract()、IBE.Enc()、IBE.Dec()四个步骤组成。其中IBE.Setup()过程负责系统参数的建立，包括系统主密钥和主公钥；IBE.Extract()过程基于系统主密钥和主公钥，针对不同的用户身份，抽样并计算对应的公钥与私钥；IBE.Enc()和IBE.Dec()过程分别为对明文的加密和解密。详细方案如下。

3.1 基本方案

定义6（FRD（full rank development）编码）[8]令任意素数q与正整数n，如果函数对任意，矩阵是满秩的且h是可计算的，则称函数h为FRD编码。

本文通过对文献[8]的改进，设计了一个身份基矩阵加密方案，将明文空间由原方案的M∈[p-1]l×l,p＜q缩减至M∈{0,1}l×l，但在同等情况下(p=2)，原方案噪声上界B满足而本文方案为B＜q/2n。因此相同情况下，本文方案容忍的噪声上界更高，具体方案如下：

（1）IBE.Setup(1λ,1l)。设λ为安全参数，l为明文维数。设定模数q为大于2的素数，随机选取整数n，以及Z上的误差分布X=X(λ)，令其最大误差满足BX≤q/2n，设m=O((n+l)lbq)与高斯参数σ。调用GenBasis(1n,1m,q) 算法生成和Λ⊥(A0) 的基，且满足。随机选择矩阵设公开参数params={n,m,l,q,A0,A1,B,U} 以及msk=，其中n、m为矩阵维数，l为明文维数，A0为主公钥，A1、B、U为随机矩阵。

（2）IBE.Extract(params,msk,id,1t) 。对任意身份id∈，计算它的FRD编码H=h(id)∈。调用SampleLeft(A0,A1+H×B,TA,U,σ) 得到W∈Z2m×l。令F=(A0|A1+H×B)，由引理2，有F×W=Umodq。设用户私钥为skid=S=，从误差分布中随机抽取E←Xn×l，令用户公钥为pkid=P=(U+2E|F)∈，则满足P×S=2Emodq。

（3）IBE.Enc(P,M)。输入消息矩阵M∈{0,1}l×l，随机选择R←{0,1}n×l，计算输出密文C=RT×P+(M|Ol×2m)modq。

（4）IBE.Dec(S,C)。给定密文，计算输出消息M=(C×S)modqmod 2。

3.2 正确性与安全性

本文设计的IBE方案是正确的且具有IND-sIDCPA安全。

（1）正确性

引理3对于消息矩阵M←{0,1}l×l以及随机选取的噪声矩阵，q为任意一个大于2的素数。解密运算M′=2E+Mmodqmod 2，满足M′=M的前提条件是2||E||∞≤q。

证明若方案正确解密，则2Emodqmod 2=0 。当2||E||∞＞q时，矩阵中至少存在一个元素2e大于q，由于q是素数，因此2emodqmod 2=1，该值会改变对应位置M′的值，导致解密失败，因此2||E||∞≤q。□

对该身份基矩阵加密方案，解密过程满足：

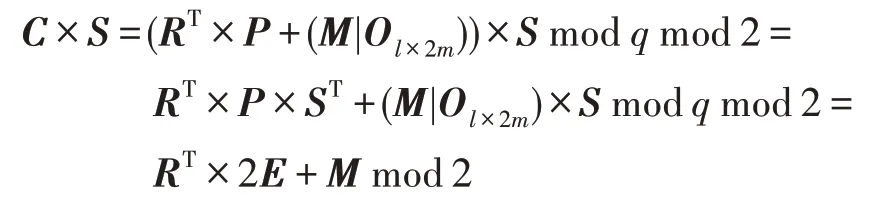
由引理3可知，当2RTE上各个元素均小于q时，方案总能正确解密。已知||E||∞≤BX,R←{0,1}n×l，故：

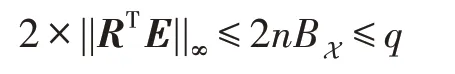
因此当BX≤q/2n时，可由C正确解密得到消息M∈{0,1}l×l，即该方案是正确的。

（2）安全性

定理3本文中的身份基矩阵加密方案的破解难度与解决广义LWEn,q,X问题等同。只要广义LWEn,q,X问题是困难的，那么本文方案是IND-sID-CPA安全的。

已知文献[8]中的方案是IND-sID-CPA安全的，本文方案中修改了公钥的产生方式，由于E是随机抽取自误差分布的小噪声，因此本文方案公钥P=(U+2E|F)与文献[8]的公钥P=(U|F)对敌手而言是不可区分的；对于id≠id*，有，当h(id)≠h(id*)时，产生的私钥在统计上是不可区分的；密文C在密文空间中是随机均匀的，因此敌手的攻击优势为零。故只要广义LWEn,q,X问题是困难的，则本文方案是IND-sID-CPA安全的。

4 身份基矩阵层级全同态加密方案

层级全同态加密即经过深度为L的计算电路后，方案能正确解密，但对L+1次同态运算后的密文，无法正确解密。本章使用3.1节的身份基矩阵加密方案，构造一个身份基矩阵层级全同态加密方案。方案实现一次全同态运算的流程如下：

（1）通过IBE.Setup算法产生L组参数以及主公钥和主私钥。

（2）通过IBE.Extract算法产生L组密钥和对应的公钥，并计算乘法密钥和哈达玛积密钥（见4.1节），以及分别对应的转置密钥（见4.2节SwitchKeyGen算法）。

（3）执行矩阵加法、乘法或哈达玛积的同态操作（见4.1节），矩阵同态加法不改变密文尺寸，可以用原私钥正常解密。若执行了乘法或哈达玛积运算，则转到下一个步骤。

（4）对由步骤（3）得到的高维密文矩阵，使用密钥转换技术（见4.2节SwitchKey算法），获得能由指定密钥解密的低维密文，同时不改变明文的值。

（5）使用模转换技术（见4.3节Scale算法），将模数由q转换为一个较小的p。经过模转换技术能将噪声缩减为原来的p/q，以支持执行更多次的同态运算。

本文方案中将密钥转换技术和模转换技术联合组成一个Refresh算法，每次执行乘法和哈达玛积运算后，通过调用Refresh算法输出的新密文可以继续进行同态运算。具体方案见4.4节。

4.1 矩阵同态运算

（1）同态加法：输入两个密钥为S的密文C1、C2，输出同态密文Cadd=(C1+C2)modq。此时满足CaddS=(C1+C2)S=M1+M2+2E′modq。故同态加法正确解密。

（2）同态乘法：输入两个密钥为S的密文C1、C2，同态乘法可表示为[C1SC2S]q=M1M2+2E′modq。根据定理2，令C*=(C1⊗C2)sr，S*=(S⊗′S)sc，有[C1SC2S]q=C*S*modq。

（3）同态哈达玛积：输入两个密钥为S的密文C1、C2，同态哈达玛积可表示为[(C1S)∘(C2S)]q=M1∘M2+2E′modq，根据定理2，令C*=(C1⊗C2)er，S*=(S⊗S)ec，有[(C1S)∘(C2S)]q=C*S*modq。

在进行同态乘法和同态哈达玛积运算后，提高了密文和密钥的维度，需要借助密钥转换技术，在不影响正常解密的前提下，对密文和密钥降维。

4.2 矩阵密钥转换技术

采用密钥转换技术对4.1节中的C*、S*进行降维，使经过同态运算的密文能继续进行同态运算。矩阵密钥转换技术用到了以下两个算法[20]：

（1）Powersof2(A)：输入一个矩阵，算法以列为单位进行操作，输出矩阵的第i列为：

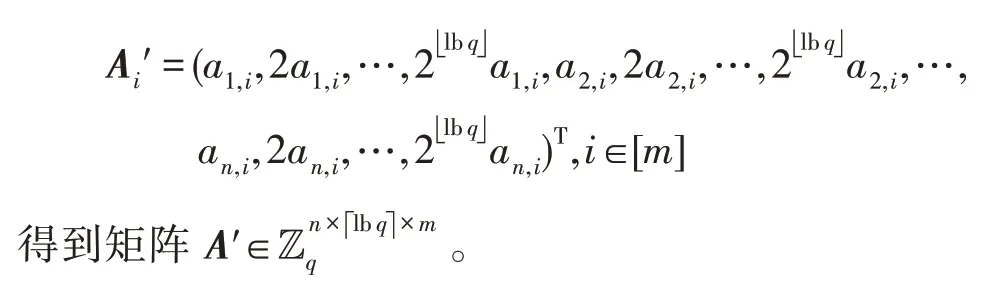
（2）BitDecomp(B)：输入一个矩阵，算法以行为单位进行操作，输出矩阵的第i行为：

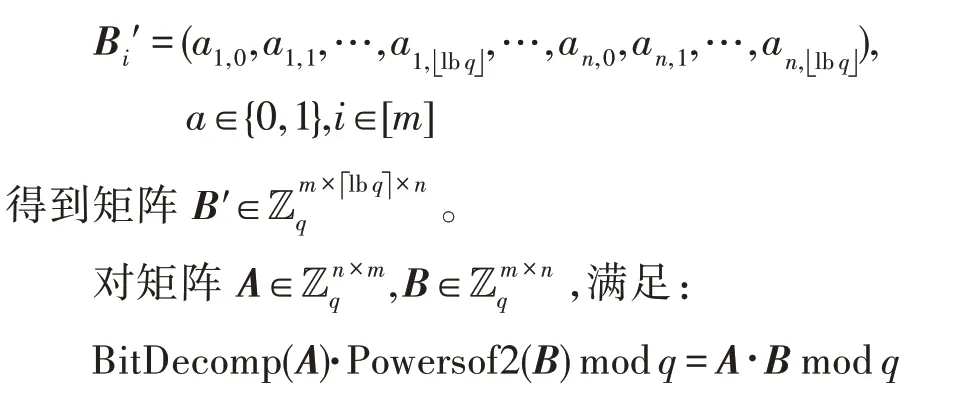
矩阵密钥转换算法包括两个过程：第一个算法以一个大尺寸的旧密钥，一个正常尺寸的新密钥以及它所对应的公钥为输入，输出一个置换密钥；第二个算法以大尺寸的旧密文以及置换密钥为输入，输出一个正常尺寸的新密文，且这个新密文能被新密钥正确解密。本文方案基于文献[16]，但引入了一个中间矩阵Z，构造一个改进密钥转换算法，这样有效减小了中间过程引入的噪声。具体过程如下：

设CaSa解密产生的噪声为2Ea。由引理3可知，只要2||E′+Ea||≤q，则新密文Cb可以被新密钥Sb正确解密。

4.3 矩阵模转换技术

通过4.2节中的密钥转换技术，降低了密文维度，但密文中的噪声没有缩减。通常，经过一次同态乘运算后，噪声会呈指数增长。模转换技术的思想是把模q的密文转换为较小的p，在这一过程中噪声会缩减为原来的p/q，并且不影响正常解密。具体算法如下：

Scale(C,q,p)：输入矩阵和整数q＞p＞2，输出矩阵C′=「p/q」C，满足C′=Cmod 2。

引理4[16]设q、p为两个奇数(q＞p)，C∈,C′=Scale(C,q,p)。对任意满足条件||[CS]q||∞＜q/2-(q/p)||S||1的S，有[C′S]p=[CS]qmod 2，且||[C′S]p||∞＜p/q||[CS]q||∞+||S||1。

在每次进行同态运算后，调用密钥转换技术和模转换技术，将密文维数降低到普通值，同时缩减噪声，以支持下一次同态运算。

4.4 本文方案

基于3.1节设计的IBE方案，结合文献[16]，构造一个层级身份基全同态加密方案。方案实现了同态加法运算（IBFHE.Add）、同态乘法运算（IBFHE.Mult）以及同态哈达玛积运算（IBFHE.PMult）。在同态运算后，通过刷新操作（IBFHE.Refresh）获得以新密钥加密的新密文。具体方案如下：

（1）IBFHE.Setup(1λ,1L,1l) ：输入安全参数λ，计算电路最大深度L以及明文矩阵维数l。令配置参数μ=μ(λ,L)=ϑ(lbλ+lbL)，随机产生整数n，令m=O((n+l)lbq)，高斯参数为σ。对k=L到0：

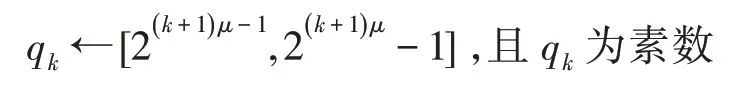
（2）IBFHE.Extract(params,id)：根据IBFHE.Setup中公开的参数以及电路深度L，采用IBE.Extract算法产生对应深度的公钥、私钥，并计算此时的乘法和哈达玛积的转置密钥。对k=L到0：

（3）IBFHE.Enc(params,pk,M)：输入明文矩阵M∈{0,1}l×l，运行C←IBE.Enc(PL,M)，得到密文矩阵C。

（4）IBFHE.Dec(params,sk,C)：对使用Sk加密的密文矩阵C，通过计算M←IBE.Dec(Sk,C)，恢复明文M。

（5）IBFHE.Add(C1,C2)：输入两个同层次密文C1、C2（当层次不同时，调用IBFHE.Refresh刷新较高层次的密文，下同），计算并输出同态加法运算结果Cadd=C1+C2。此时对应的私钥不变。

②模置换过程：运行C**=Scale(C*,qk,qk-1),得到模为qk-1的密文C**。

4.5 噪声分析与安全性

（1）加解密的噪声

设密文C的密钥为Sk，公钥为Pk，满足PkSk=2Ekmodqk，其中则。由引理3，当1+2nBX≤qk/2时，方案总能正确解密。

（2）同态运算的噪声

设C1、C2是密钥为Sk的两个密文，其噪声分别记为，设两者的噪声上界均为B。对于同态加法运算，输出密文最大噪声为2B。对于同态乘法运算，对于同态哈达玛积运算，。由引理3，如果这些噪声小于qk/2，那么后续能正确解密。

（3）IBFHE.Refresh算法的噪声

Refresh算法由Switch算法和Scale算法组成，在3.2节中证明了Switch算法的正确性，有。由引理3，只要保证最终噪声小于qk/2，那么方案能正确解密。对任意，由引理4，当时，方案能正确解密，且

（4）安全性

IBFHE方案的安全性与IBE方案的安全性密不可分，定理3说明了本文中的IBE方案是IND-sIDCPA安全的，而IBFHE方案中，同态计算算法是公开的，不影响系统安全性；此外，IBE方案中对明文0或1的加密结果，具有不可区分性。而IBFHE方案是多个IBE密文进行计算的结果，同样具有不可区分性，因此本文IBFHE方案也是IND-sID-CPA安全的。

4.6 性能分析

从理论和实验结果上可以证明，本文方案在密钥转换过程中引入的噪声值要远小于文献[16]中提出的方案。

4.6.1 理论分析

本文提出的身份基矩阵层级全同态加密方案，能一次加密一个l×l维的0、1明文矩阵，并实现了矩阵加法同态、乘法同态以及哈达玛积同态。方案中使用的矩阵拉伸和提取操作是实现矩阵同态运算的重要理论基础。矩阵密钥转换技术是实现全同态加密的重要操作，但执行该步骤的同时也会引入新的噪声。相较于文献[16]，本文中的改进密钥转换技术，不仅支持对任意维度的公钥进行密钥转换，还大幅减少了噪声的增长。具体数据见表1。

Table 1 Comparison of efficiency between proposed scheme in this paper and ref.[16]表1 本文方案与文献[16]的效率比较

其中n为随机整数,l为进行加密的明文矩阵维数，m=O((n+l)lbqk)，t为文献[16]中定义的变量，值为(m+l)2ll bqk，n远小于t。可见，本文方案的私钥略大于文献[16]，但在控制噪声增长上具有很大的优势。本文方案的密钥转换过程中引入的噪声，主要受初始噪声和矩阵尺寸参数n影响，而文献[16]的方案中，t是多个矩阵尺寸参数与l bq相乘的结果。在一次密钥转换后，文献[16]引入的噪声为初始噪声的t倍，而在初始噪声相同的情况下，本文方案引入的噪声仅为文献[16]方案的n/t，并且不会受到其他参数的影响。

4.6.2 实验证明

（1）实验条件

本文方案仿真实验说明如下：

硬件条件：本文使用九代i5处理器，主频2.4 GHz，16 GB内存。

软件条件：Win10_64位操作系统，编程软件为Python3.8。

（2）实验目标

本文方案的验证指标主要是密钥转换过程中引入噪声大小，噪声越大表明性能越差。因此，为比较本文方案与文献[16]在密钥转换过程中的噪声增长大小，实验中对两种方案分别使用两个相同明文进行加密与同态乘法运算，得到100个计算结果中的噪声矩阵。由噪声矩阵的范数值大小作为该过程引入噪声的参考值，该值越大表明方案引入的噪声越大，性能越差。

（3）实验过程

本实验分别对本文方案和文献[16]方案，编写程序实现下述过程，得到密钥转换过程中引入的噪声：

①设定初始参数n、l、q，明文矩阵M1、M2←{0,1}l×l，计算得到m、t。

②根据Extract方法，产生两组公私钥对Sa、Pa与Sb、Pb。

③根据Enc方法，使用Sa分别对M1、M2进行加密，得到密文矩阵C1、C2。

④由4.1节方法，计算得到进行同态乘法或同态哈达玛积运算后的密文和密钥

⑤使用对应的密钥转换算法，得到以Sb加密的密文Cb。

⑦重复执行步骤②～⑥，得到多个实验结果。

（4）实验结果

在本次实验中，设初始参数n=2，l=3，q=1 021，令m=n+l=5，t=(m+l)2ll bq=1 920。对明文M1=进行同态乘法运算，得到10组实验数据，每个数据都是10次运算结果的平均值，具体数值见表2。将这10组数据绘制成直方图，见图2。可以看出，文献[16]在一次密钥转换过程中引入了大量噪声，其值均大于q/2，而本文方案引入的噪声明显较小，并且在本次实验中仅为文献[16]的0.23%。由于t是随着n的增大而指数增大的，因此n/t的值会越来越小，故本文方案的提升会越来越明显。因此本文方案的性能更好。

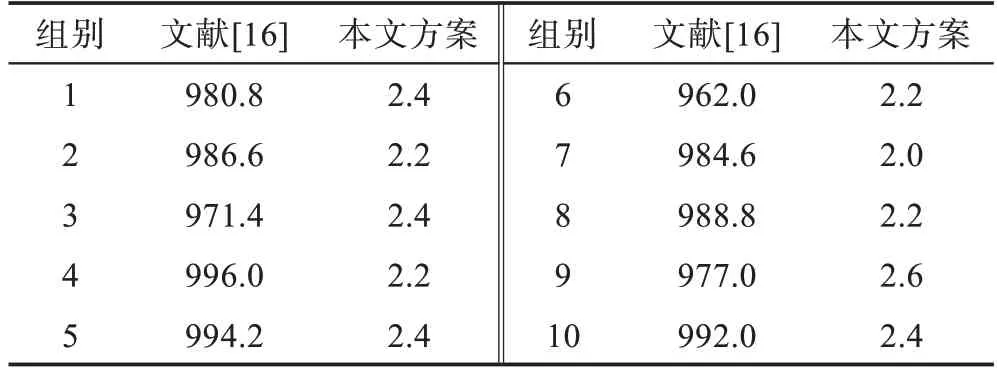
Table 2 Results of experiment表2 实验结果

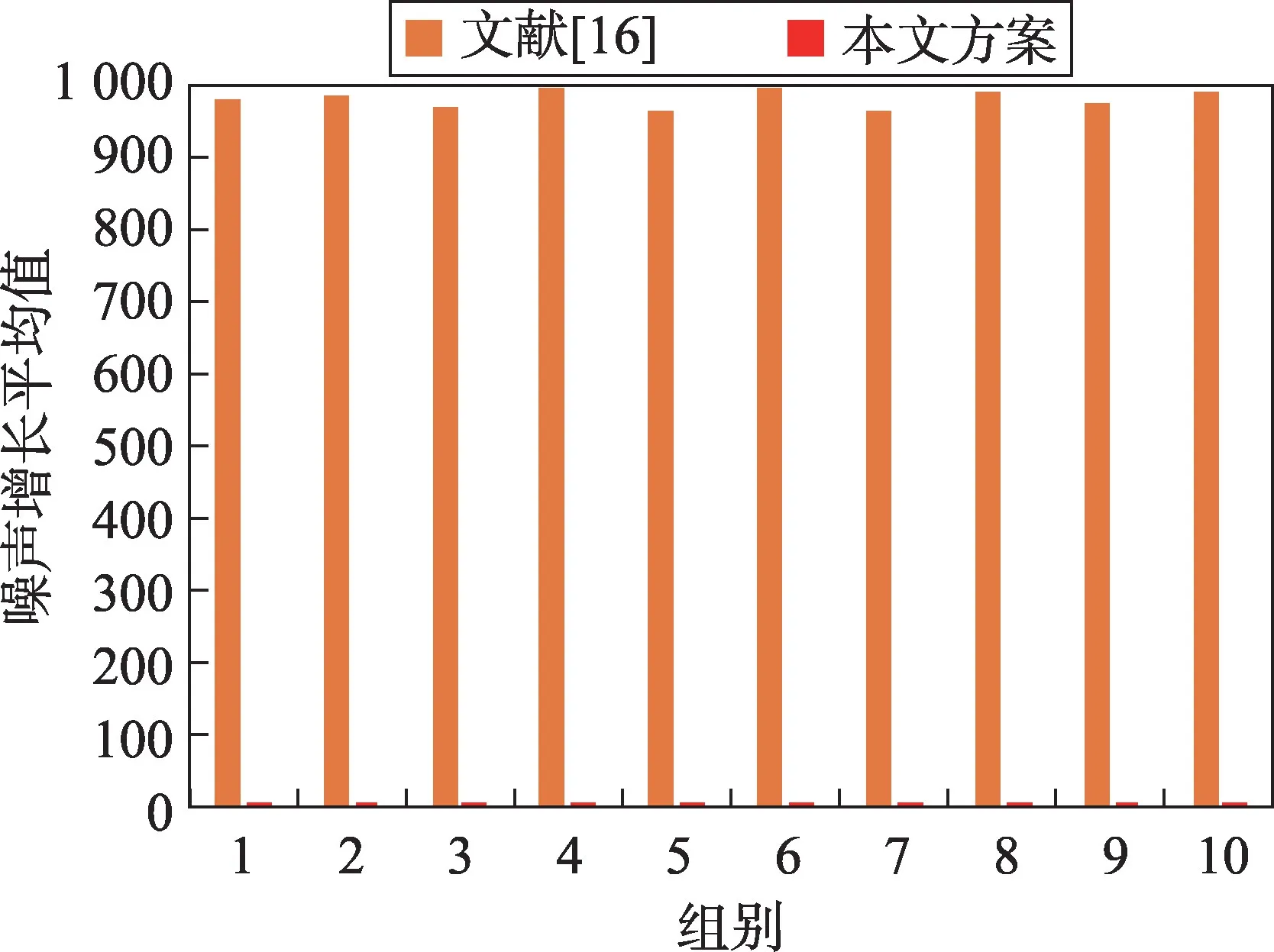
Fig.2 Histogram of noises图2 噪声直方图

5 结束语

本文方案基于格上LWE困难问题，构造了一个基于身份的矩阵层级全同态加密方案，通过密钥转换技术降低同态运算密文的维度，使用模转换技术减小了噪声。采用矩阵存储结构，可以实现矩阵的同态运算，因此本文方案是IND-sID-CPA安全的，同时具有较小的公钥尺寸和较高的加密效率。方案还有许多可以改进的地方：一方面可以利用Bootstrapping技术，实现全同态加密；另一方面，可以基于本文方案，构造多用户情况下的矩阵全同态加密方案。