有机太阳能电池材料中电荷转移态

郑子龙， 周荣锟， 胡双媛， 王如志， 张永哲

(1.北京工业大学材料科学与工程学院， 北京 100124； 2.新型功能材料教育部重点实验室， 北京 100124；3.固体微结构与性能北京市重点实验室，北京 100124)

传统无机半导体中，自由载流子由活化层吸收光直接产生，而有机材料组成的光电器件吸收光后，通常会产生空间受约束的电子- 空穴对，即Frenkel型激子. 因此，当有机太阳能电池(organic solar cell, OSC)的活性层基于单一组分时，激子分离效率非常低[1]. 为此，通过使用包含2种组分的活化层来克服此问题，即活化层为电子给体- 电子受体(donor-acceptor, D-A)双层或混合异质结(bulk heterojunction, BHJ)型的材料[2-4]. 与双层结构相比，混合异质结可在 D-A界面处产生大量激子，增加了自由电荷的产生. 因此，目前高效的有机太阳能电池的活化层都使用了混合异质结结构. 自从20世纪90年代中期引入混合异质结以来，得益于非富勒烯受体(non-fullerene acceptor, NFA)的快速发展[5-9]，有机太阳能电池的能量转换效率(power conversion efficiency, PCE)得到了极大的提升，目前单结能量转换效率接近17%[10].

与无机太阳能电池相比有机太阳能电池的一个关键特征是在D-A界面处出现了电荷转移(charge-transfer, CT)态，即全部或部分电荷从D转移到A时形成的电子态. 在D或A组分中光产生的激子可以在D-A界面解离，导致电子和空穴分别分布在受体和给体材料中，此时它们之间仍存在着库伦相互作用力，并把这个过程称为CT态的形成[11-12]. CT态可以进一步形成自由载流子，也可以通过辐射或非辐射复合退变回电子基态. 因此，CT态控制着光生激子解离、自由载流子生成以及(辐射和非辐射)复合过程[11-15]. 有机太阳能电池中，CT态处于光电转换物理过程的核心地位，因此，它成为理论[16-35]与实验[15, 36-45]共同的研究热点.

本文主要简述了研究D-A界面处CT态的理论和实验方法，阐明了电子给体和电子受体的分子堆积、极化效应、CT态无序分布以及激子之间的相互耦合等因素如何影响CT态的性质和复合过程[17, 29-30, 45-46]；同时，基于前期对富勒烯和基于非富勒烯受体材料的研究，阐述CT态与有机太阳能电池的性能之间的物理联系.

半经典框架中的两态模型在有机太阳能电池文献中一直被用来描述涉及CT态的光吸收和复合过程，因此，将用该模型简要讨论用于估算CT态能量的研究方法，其中包含实验测量和理论计算，这些方法可提供有关活化层微观结构的整体和局部特性信息，并说明界面对CT态能量的影响. 此外，作者描述了CT态与电池开路电压损耗之间的联系，概述了降低电池能量损失的有效方法. 最后，本文重点介绍了能量转移效率超过20%的有机太阳能电池所面临的挑战和未来工作.

1 电荷转移态的光谱和复合过程

有机太阳能电池中光诱导的载流子形成过程如图1所示，激子单重态和三重态主要局域分布在电子给体(或电子受体)组分，激子扩散到D-A界面处解离形成CT态；电子与空穴(分别位于电子给体、电子受体)分布较远时，彼此的相互作用趋于零，并进一步分离形成自由载流子，即电荷分离(charge separation, CS)态. 另一方面，自由载流子也可以结合形成CT态，并通过辐射、非辐射复合跃迁回到电子基态. 本文中讨论的速率常数k表示电子在各种电子态间转移过程的跃迁速率常数(包括辐射和非辐射跃迁速率，分别用kr和knr表示).

1.1 CT态的吸收和发射光谱

热和光(吸收和发射)引导电子转移过程是相互联系的，Hush等[47-48]和Mulliken等[49]根据半经典两态Mulliken-Hush模型，发现从基态到CT态的吸收能具有高斯分布特性(使用谐振子模型和线性电子- 振动耦合的近似结果)，并且给出了CT态能带谱的性质[47，50]

(1)

(2)

(3)

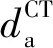
(4)

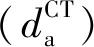
(5)

式(5)中推导给出的ΔdCT可以带入式(4)中，被称为广义Mulliken-Hush表达式，对于强耦合和弱耦合的D-A体系都可适用[49]. Mulliken-Hush表达式的意义在于，它直接将电子态之间耦合强度与电子态吸收谱联系起来. 在式(1)中，A(ν)为摩尔消光系数，指前因子A0[51-53]由

(6)

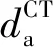
(7)

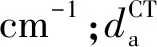
但是，在许多有机太阳能电池材料中CT态吸收光谱非常弱. 因此，需要高灵敏度的技术来检测这些状态，例如光热偏转光谱或傅里叶变换光电流光谱[11,36,44,54]. 尽管常规分析CT态吸收光谱可以获得重组能和驱动力，但难以从中估算与CT态相关的电子态耦合强度[55-56].

对于CT态的发射光谱，在半经典两态Mulliken-Hush模型中，其计算公式为

(8)

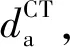
根据式(2)，EQEPV对ν的依赖性公式为

(9)

(10)

式中：l为薄膜厚度；NCT为CT态的密度(即每能量单位的电子态数目数)；η为内量子效率(即电池产生的自由载流子数目同入射光子数目的比值).

1.2 CT态辐射复合过程

无论是哪种类型的太阳能电池，CT态的辐射复合对于确定电压损耗至关重要. 辐射复合速率kr由爱因斯坦系数关系

(11)

(12)

式中，νem是CT态发射峰边缘处对应的出射光子频率. 实验上，根据CT态的测量寿命τ和光致发光量子产率Φr，可以估算辐射复合速率kr=Φr/τ.

1.3 非辐射复合

在半经典两态模型中，非辐射复合速率knr描述了从CT态到基态的跃迁过程，其速率可用Marcus公式估算[51]，公式为

(13)

2 CT态的量子力学描述

有机太阳能电池中高分子聚合物分子量很大，只能使用密度泛函理论(density functional theory, DFT)方法来研究界面处的CT态. 由于传统DFT方法的缺陷，不足以合理描述聚合物共轭高分子，更不适用于在这些高分子界面处的CT态[59]. 这主要是因为标准的交换相关函数和杂化密度泛函(例如非常流行的B3LYP函数)不能提供正确的库仑势渐近行为(即1/r，其中r是2个电子之间的距离)，从而导致电子间相互作用误差过大[60-61]，非局域现象显著.

为解决这些问题，对CT态的理论研究开发出新的密度泛函，称为范围划分杂化(range-separated hybrid, RSH)泛函[18, 22-24, 59]. RSH泛函是将2个电子之间的库仑相互作用和交换积分分为短程区域和长程区域. 通过最小化误差函数，实现不依赖实验数据，计算自洽的DFT函数调控[26]

(14)

式中：右侧的第1项和第2项分别对应库仑势的长程和短程作用；ω为分割长程、短程范围的调控参数. Hartree-Fock交换积分提供了正确的库仑渐近行为，用于描述远程作用；而短程库仑势常使用局域杂化DFT函数进行处理. RSH泛函可以准确地描述孤立系统中的CT态， 对不同的分子体系，分割参数ω通过自洽优化的方法得到，常用的方法之一为最小化目标函数J(ω)[26].

J(ω)=(εHOMO+IP(ω))2+(εLUMO+EA(ω))2

(15)

式中εHOMO和εLUMO分别为最高占据分子轨道(highest occupied molecule orbital,HOMO)和最低未占据分子轨道(lowest unoccupied molecule orbital, LUMO)的能量. 由于D-A复合物的HOMO主要位于D上，而LUMO则主要位于A上，原则上-εHOMO必须等于分子的第一电离势(ionization potential，IP)[62]，-εLUMO必须等于分子的第一亲合势(electron affinity，EA)，而实际上长、短程分割参数的调整有效地考虑了D分子和A分子对CT态的贡献. 目标函数的作用是使-εHOMO和IP(ω)之间的误差以及-εLUMO和EA(ω)之间的误差最小化，得到参数ω.

通过上述自洽方法优化RSH泛函参数(即在真空中，以下称为Optimally-turned(OT)-RSH/ωVAC，对并五苯-C60复合物模型(见图2(a))进行了CT态的理论模拟，与实验测量结果相比，计算的CT态能量被高估[22-24]，其原因在于该理论模拟并未考虑体系外极性介质的影响. 为此，重新将介质对CT态能量的影响纳入其中. 最简单的方法是将OT-RSH计算与极化连续介质模型(polarizable continuum model，PCM)结合在一起，以提供隐形介质的效果. 随后这种模型在从头算量子化学计算CT态方面得到了广泛应用. 但当使用ωVAC值时，PCM模型对εHOMO、εLUMO和CT态能量的影响很小(<0.1 eV)[21，63-64]，而且对CT态的估算还存在较大偏差.

为了克服RSH模型中的这个问题，Zheng等[21，31]又相继开发出2种方法. 第一种是保留极性连续介质模型，对ω参数进行优化(即OT-RSH/ωPCM，其中ωPCM在PCM模型中获得)[21]. 用含时密度泛函理论(time-dependent density function theory，TD-DFT)计算得到的结果显示激子能量受ω参数的影响不大，但随着外界环境介电常数的增加(即ω参数迅速减小)，CT态能量会大幅降低(见图2(b)). 考虑了介质极性效应的并五苯-C60复合物，用ωPCM得出的最低CT态能量(1.2 eV)与实验值测量值(1.2～1.3 eV)相一致[38]. 原则上，同一分子体系中电子密度分布变化不大时，ω参数应尽量保证没有大幅变化；分子间相互作用较弱的复合物，在受到极性环境的影响时，电子密度分布不应该有剧烈变化，因此，此方法缺乏一定的物理依据[65-66]. 另外，这种方法必须再次优化ω参数，得到与ωVAC值差异很大的ωPCM[21, 63-65].

为了进一步解决上述问题，开发了更复杂的密度泛函方法——介电屏蔽范围划分杂化(screened range-separated hybrid，SRSH)泛函，其优点是可以用与ωVAC相同的ω参数[31]. 库仑势由2个参数α和β调整[66-67]，公式为

(16)

式(16)右侧的两项对应电子间库仑势的长程、短程部分. 长程范围的电子波函数采用Hartree-Fock来处理积分；短程范围的用纯DFT泛函处理电子波函数积分. 第一项为此泛函重点修正部分，长程范围处演化为(α+β)/r，可通过调控环境极性，实现真空到极性介质中长程库仑作用的调整. 在理想真空介质情况下，(α+β)的数值为1；在极性介质中为1/ε，其中ε对应介质的介电常数[68].

(17)

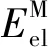
由于静电库伦势Eel是一个负项，所以，预测随着1/ε的增加，CT态能量(ECT=ΔE-Eel)应减小，但ΔE随1/ε的增加，与Eel相比增幅更大，因此，综合考虑能隙和库仑势的变化，CT态能量将随1/ε的增加而增加，见图2(c). 实验已观察到多个有机太阳能D-A异质结中ECT和ΔE随ε的增加而降低[69-70]的现象. 尽管较强的极性介质会降低库仑作用，促进CT态的解离，从而促进自由载流子的形成(这是一个对光伏电池有利的方面)，但ECT和ΔE的减小会导致开路电压VOC降低，不利于光电转化效率. 从这些结果中得出的重要信息是，采用强极性的有机材料，一定要设计好D组分的第一电离势和A组分的第一亲和势，以便从高介电常数环境中受益，保证更多自由载流子的生成，减少VOC损耗.

3 界面形貌对CT态能量分布的影响

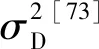
(18)

在无定形固体中，除了动态无序之外，还有第2种使CT态能量加宽的机制，即静态无序σS. 静态无序反应了混合异质结的不定型本质，它来源于D分子、A分子原子坐标甚至震动模式的非对称结构，不依赖时间而变化. 总能量分布(σT)是静态分量和动态分量的组合. 当静态和动态能量无序均为高斯分布时，总无序的标准差σT[15,73-74]可以表示为

(19)

目前讨论的量子化学计算中考虑的D-A配合物只有一个D分子和一个A分子. 然而，当在D和(或)A材料的界面附近存在有序的纯相时，空穴和电子可以在几个分子(或聚合物链)上离域. 因此，许多实验和理论研究了波函数离域化程度对输运态和CT态的影响，进而了解电荷分离和电荷复合过程[16,19,25,28,39,45,79-80]. 以戊烯-C60复合物为模型，基于分子动力学产生的含有若干D和A分子的复合物进行密度泛函分析，计算结果表明电荷离域化的增加(如介质介电常数的增加)可使电子-空穴结合能下降，有利于电荷分离，但是这会降低最低的CT态能量，大大增加了非辐射衰减率，最终导致VOC损失[27-28,45]. 因此，这些结果表明需要平衡在电荷离域带来的有利和不利影响，不能忽略电荷离域、极化和无序的共同影响.

4 CT态与开路电压(VOC)的关系

在有机太阳能电池中，测得的VOC值通常低于无机或钙钛矿光伏器件中的VOC值. 前者偏低主要归因于CT态能量通常低于光学能隙，该光学能隙对应于D或A材料中的激子能量. 对大多数混合(D-A)异质结的研究表明，其VOC与CT态能量相关[11,42](见图4(a)(b)). 电压损失的主要来源与CT态到基态的非辐射衰减有关[42]. 在基于富勒烯的有机太阳能电池中，无辐射电压损耗(ΔVnr)通常约为0.40 eV，而在基于高效GaAs的器件中，其值只有0.04 eV.

EQEEL可以量化ΔVnr的值

(20)

式中q表示一个电荷的电量. 当只考虑CT态时，EQEEL由CT态到基态的kr和knr衰减率确定[42].

(21)

式(1)(2)代入式(21)可知，ΔVnr应随着CT态能量的降低而增加，实验已观察到这种趋势[42].

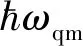
(22)

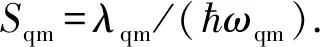
虽然静态无序在原则上可以通过制备有序的D-A结构来消除，但λqm量子动力学无序与分子内振动有关. 因此，λqm是一个分子的内禀性质. 由于λqm的影响是无法避免的，因此，可以得出结论[42]：单结OSCs不能达到Shockley-Queisser PCE(极限值为33.5%)[83]，而当材料的光学带隙为最佳值(1.45～1.65 eV)时，PCE达到最大极限为25.5%. 但是必须强调的是，这一结论的成立是假定CT态是辐射和非辐射复合的唯一途径.

如上文所述，由于ΔVnr的降低，CT能量的增加有利于提高有机太阳能电池效率. 因此，最近的实验工作侧重于研究D:A活化层，其中CT态和激子(local exciton，LE)能量简并成为设计高效电池的重要设计原理[5-8,10,14,84-88]. 混合异质结中光学能隙由D(或A)组分决定，通过研究D和A的EA差(ΔEEA=EAD-EAA)或IP差(ΔEIP=IPD-IPA)，寻找CT态和LE能量简并的材料(ΔELE-CT～0 eV )(见图5(a)). 许多新的NFA材料展现出高效特点[5-8,10,86-88]. 2019年初，基于PM6:Y6共混物的单结太阳能电池的PCE高达15.7%[10]，其中ΔEIP=0.09 eV. 对于聚合物：NFA共混物，已获得PEC高达10.4%的有机器件[88].

ΔELE-CT值较小的2个结果是，CT态可以更容易地与LE态混合，有利于从CT态转化到LE(见图5(b)(c)). 因此，简并的LE、CT态，通过LE打开了从CT态到基态的额外辐射弛豫路径. 因此，制定了2个高效器件的设计规则，以尽量减少开路电压损失[7]，这2个规则是：1) D和A分子态的IPs和EAs之间的能量越小越好；2) D或A材料的光致发光量子产率越大越好.

根据这些规则，研究者们开发了一系列D:A体系，将有效光电流产生与高EQEEL值结合起来，使ΔVnr值减小到0.21 eV[7]. 而在有机太阳能电池发展的早期阶段，研究的重点是光生激子的快速猝灭[89].

因此，具有大EQEEL的强发光D:A混合物可能是实现高性能OSCs的关键步骤. 与基于两态模型[42]得出的结论相反，基于NFA太阳能电池的结果表明，实现具有与其他光伏技术相当效率的OSCs没有内在限制.

由于ΔELE-CT是LE解离的驱动力，在一系列聚合物：NFA共混物中，其中ΔELE-CT很小，测得的LE解离速率可以比典型的聚合物——富勒烯共混物的解离速率慢约100倍[7]，而且这样的速率仍然允许器件产生高光电流. 因此，超快激子解离并不是高效率OSCs的必要条件，还需要LE解离成CT态、CT态解离成自由电荷的速率远大于复合速率.

虽然CT态发光的增强降低了ΔVnr，但评估这一增强是否会对VOC和VOC,rad(其中VOC=ΔVOC,rad-ΔVnr)的辐射成分产生负面影响是很重要的. 至少对于导致LE和CT态混合的小的ΔELE-CT值，这种影响不应是有害的，因为这种混合只会导致发射和吸收强度的光谱再分配. 因此，对最终决定VOC,rad的短路和辐射电流密度不应该有任何显著的影响.

上述设计规则还解释了为什么聚合物：富勒烯共混物通常表现出低的PCEs，即使在低LE分离驱动力(即小的ΔELE-CT值)的情况下也是如此[90]. 富勒烯中最低的LE(约1.7 eV)只有微弱的吸收，光致发光效率很低[91]. 因此，在混合物中，LE基本在D上形成，当ΔELE-CT相当大时，有很大的电压损失，PCE受到限制. 当ΔELE-CT很小时，效率取决于LE的能量是在D还是A上更低. 在后一种情况下，较小的ΔELE-CT将导致LE(最初在给体上形成)的分离和LE非辐射复合之间的竞争；此外，任何CT态与LE的混合都不会增加辐射复合，因为富勒烯只是弱发射. 相反，当低能LE在给体上时，如果给体是高发光的，则共混物满足上述2个设计规则，其电压损耗将减小. 在PNOz4T:PC71BM和PIPCP:PC61BM混合异质结中(如图5所示)电压损耗很小，ΔELE-CT值很小，聚合物中激子能量比富勒烯的低[84-85].

PNOz4T:PC71BM和PIPCP:PC61BM异质结的相关研究结果表明，基于富勒烯的太阳能电池的电压损耗也可以降低. 然而，非富勒烯材料提供了更多的优势：它们可以具有高的光吸收性，提供与给体材料互补的吸收光谱并具有强的发光性. 因此，基于非富勒烯材料的进一步发展将继续推动有机太阳能电池性能的提高.

5 结论

1) 回顾了各种微观物理参数(如局部形貌、极化作用、电子态的离域和无序)对CT态的影响，以及CT态是如何通过振动或光诱导过程形成的. 但是，目前仍然缺少关于CT态如何拆分为自由载流子的完整描述.

2) 最近在理论方法上的发展使人们有可能利用固体材料中的极化对能隙以及电子和空穴相互作用进行调控. 这些技术的应用为设计有机材料提供了新途径，有机材料得益于极性增加的介质环境，可更容易进行电荷分离，但不能以降低VOC为代价.

3) 非富勒烯的研究表明，当CT态和激子能量简并时，光致发光产率很高，导致VOC损失大幅减少. 若电荷分离过程变缓，伴随开路电压损耗增加的同时，短路电流也会降低，进而减小光电效率. 通过理论结合实验的方法，可改进分子结构，提高有机太阳能电池混合异质结材料中分子排列的有序性，增强分子内、分子间的共轭效应，从而增加电荷分离和传输速率，实现开路电压和短路电流同时增加.

4) 本文没有提到的一个方面是三重态电子态的作用及其对器件性能的影响. 当最初分离的电荷复合时产生的CT态遵循量子力学自旋统计原则， 25%为单重态、75%为三重态. 这些三重CT态可驰豫到能量更低的三重态激子，从而打开另一个能量损耗通道. 因此，有必要在这个问题上开展更多的工作，特别是在非富勒烯材料中. 此外，了解如何最大限度地提高三重态和单重态CT态之间的系间窜越率(就像在热延迟荧光- 有机发光二极管材料中的光电物理过程一样)可帮助克服这些能量损耗.