基于非完美信道信息的协作NOMA 系统中保密通信技术研究

陈 杨，张忠培，李彬睿

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

非正交多址接入(NOMA)技术能显著提高频谱效率，因此被视为第五代移动无线通信系统中的关键技术[1]。与传统的正交多址接入技术(OMA)不同，NOMA 技术利用功率域来同时为多个用户提供服务[2]。由于NOMA 技术在提高频谱效率和增大覆盖面积方面的性能表现优秀，协作NOMA技术成为了近年来研究人员关心的热点[3]。

由于无线信道的开放特性，协作NOMA 系统的安全性面临严峻考验。近年来，作为新兴的有效抗窃听方案，物理层安全技术吸引了研究人员的广泛关注且被应用在协作NOMA 系统中[4-6]。文献[4]在协作NOMA 系统中讨论了放大转发(AF)和解码转发(DF)协议，并推导了保密中断概率(SOP)和保密速率表达式。文献[5]分析了干扰者协助的协作NOMA 系统中，采用随机和max-min 两种中继选择方案得到的分析和渐进SOP 表达式。文献[6]提出了一种新的非正交干扰DF 方案来提高协作NOMA 系统的保密速率并且减少信息泄露。

然而，在上述关于协作NOMA 系统的工作中均考虑的是主信道的信道信息基站和协作节点完美已知的情况，在实际应用中这是不容易实现的。非完美信道信息会导致严重的安全性能下降，因此在协作NOMA 安全传输系统中讨论非完美信道信息是很有必要的[7-10]。文献[7]推导了非完美信道信息条件下认知无线电中继NOMA 系统的中断概率表达式。文献[8]讨论了两种信道不确定模型，并以此为基础研究了协作无线携能NOMA 通信系统中波束赋形和功率分配设计的问题。文献[9]将小区边缘用户用作DF中继来协助信息传输，并研究了非完美信道信息对协作无线携能NOMA 通信系统性能的影响。考虑配置多天线的基站，文献[10]对非完美信道信息场景中协作无线携能NOMA 物联网系统的容量进行了分析。

但目前还没有讨论对非完美信道信息场景中，引入协作干扰者帮助的协作NOMA系统中基于保密中断概率限制条件的保密速率最大化问题。基于此，本文考虑了两用户多输入单输出(MISO)协作NOMA 系统，在这个系统中，一个用户(LU1)有较高的速率和安全要求(例如银行工作人员、政府工作人员等)，而另外一个用户(LU2)仅有服务质量QoS 限制(例如公共天气预报)[11]，并对该系统在非完美信道信息条件下保密速率最大化的问题进行了研究。同时考虑两个用户保密需求和速率需求，本文提出了一种自适应功率分配算法来使得保密速率最大化。此外，本文将LU1 的保密速率与LU2的传输速率之和定义为有效和速率，将有效和速率与总功率的比值定义为有效能量效率并进行讨论。仿真结果验证了本文所提出算法的有效性，并阐述了非完美信道信息对系统性能的影响。

1 系统模型和问题阐述

1.1 系统模型

本文讨论的MISO-NOMA 系统模型如图1 所示，一个基站(Alice)同时对两个单天线用户(LU1 和LU2)进行通信，系统中存在多个单天线窃听者对LU1 的信息进行窃听。与此同时，引入了一个协作干扰者(Charlie)来增强系统的安全性能。Alice 和Charlie 分别配置了 Na和 Nc根天线，其中Nc>2。此外，窃听者的集合定义为M ≜{1,2,···,M}。

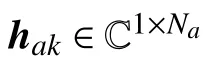
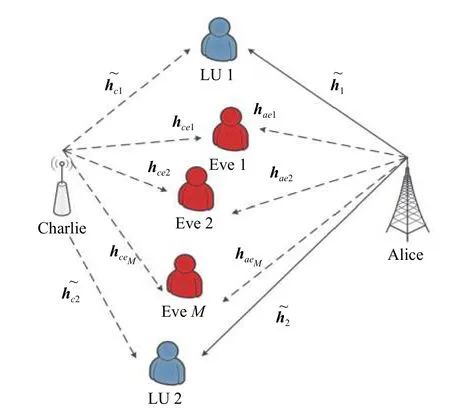
图1 协作MISO-NOMA 安全传输模型

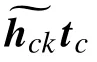
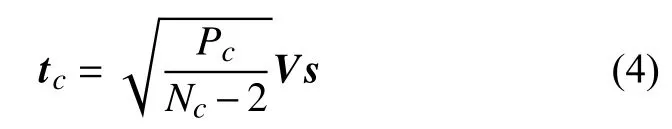
根据式(1)和式(2)，用户k和窃听者 m的 接收信号可分别表示为：

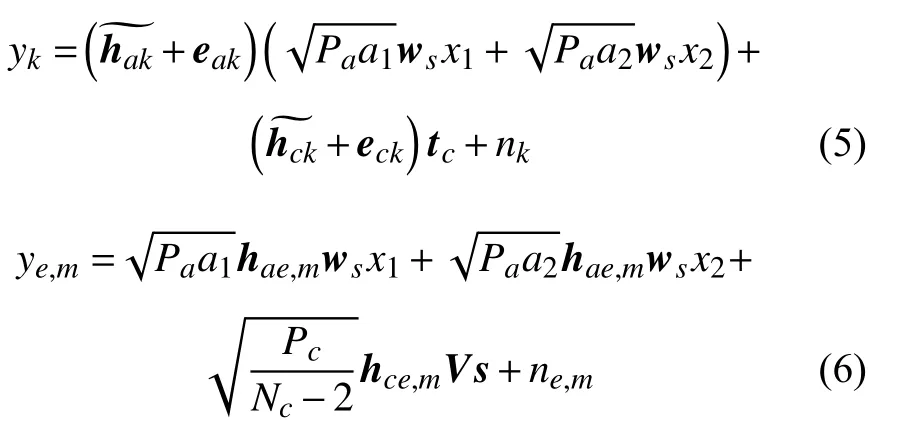
式中， nk和ne,m∈CN(0,1)分别表示用户k和窃听者m的加性高斯白噪声。

在NOMA 系统中，用户利用连续干扰消除(SIC)来检测接收到的信号。因此，LU1 首先将x1视为噪声来解码 x2，然后利用SIC 消除 x2来解码需求的信号 x1。根据文献[8]，信道估计误差所产生的噪声和终端噪声可以视为高斯噪声。综上，LU1 和LU2 的信干噪比(SINR)可以分别表示为：

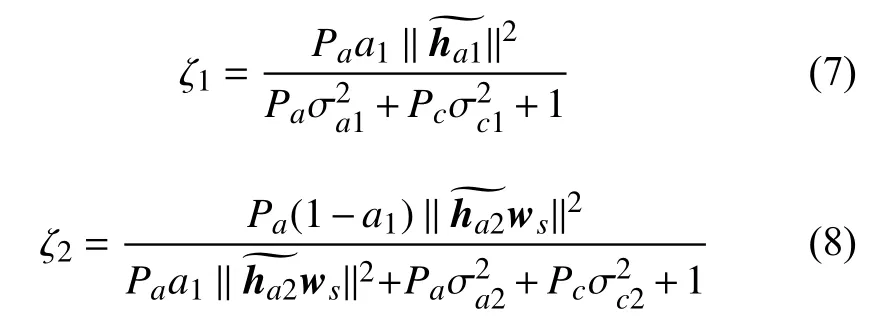
窃听者 m关于信号 x1的SINR 可以表示为：

本系统中，为了实行保密传输，Alice 采用了Wyner 编码方案，则用户的码字速率和保密速率可以分别表示为Rk=log2(1+ζk),k ∈{1,2}和 Rs，冗余速率Rk−Rs可以被利用来对抗窃听。由文献[12]和[14]可知，在非协作窃听场景中，最大被窃听信息由所有窃听者中最大的SINR 决定，因此Ce=log2(1+maxm∈Mζe,m)。当Ce>Re时，系统保密传输中断。综上，用户LU1 的保密中断概率(SOP)可以表示为：

1.2 问题描述

为了描述最优化问题，首先定义LU2 需求的最小传输速率为 Rth，则受一定保密中断概率约束的保密速率最大最大化(SRM)问题可以描述为：

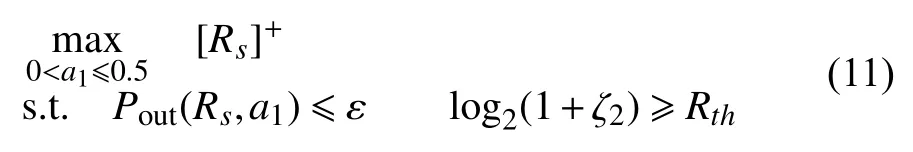
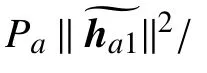
2 自适应功率分配方案

本节提出了一种有效的自适应方法来最大化式(12)中的保密速率 Rs。值得注意的是，观察式(12)， a1的取值需要在一定的范围内才能满足用户LU2 的QoS 限制。如果Alice 无法对LU2 提供服务，那么Alice 将会执行文献[14]中的协作干扰(CJ)方案来保障用户LU1 的保密通信。

2.1 重新描述SOP 限制

首先假设式(12)中的用户LU2 的QoS 限制条件已经满足。为了简化分析，定义εm=Pr(ζe,m>δ)，m ∈M，此外还定义如下这些新变量：

借助随机理论知识，易得T1,m～Exp(κ1,m) ；T2,m～Exp(κ2,m)； κ1,m=1/Paa1；κ2,m=1/Pa(1−a1)； Exp(λ)表示参数为 λ的指数分布。根据文献[12]，矩阵hce,m的元服从独立的CN(0,1)分布，因此其每个元的模的平方服从均值为1 的指数分布。可以得到∥hce,mV∥2～Γ(Nc−2,1)，其中，Γ(α,β)表示形状参数为 α，逆尺度参数为 β的伽马分布。进而可以推出T3,m～Γ(Nc−2,κ3,m)， κ3,m=Nc−2/Pc。综上，式(12)中的SOP 表达式可以重写为：

综合式(13)～式(17)，再参考文献[14]，可以得到 εm的一个闭式表达式。由于篇幅限制，这里省略具体计算过程。因此， εm可以重写为：

由于本文考虑多个非协作窃听者场景，由文献[12,14]，每个窃听者的SINR 是相互独立的。因此式(12)中的SOP 限制可以改写为：

定义ρ(a1)=δ/a1； A(a1)=1+(1−a1)ρ(a1) ；B(a1)=1+Pcρ(a1)/(Pa(Nc−2))。将式(18)带入式(19)中，可得：

2.2 功率分配最优化

讨论功率分配的优化首先需要考虑式(12)中用户LU2 的传输速率限制。可通过计算得到 a1取值的上界：

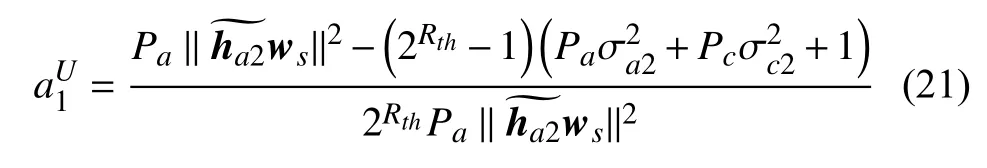
观察式(20)，可知ρ(a1)>0。对式(20)两边关于 a1进行求导，经过一些等式变换可得：

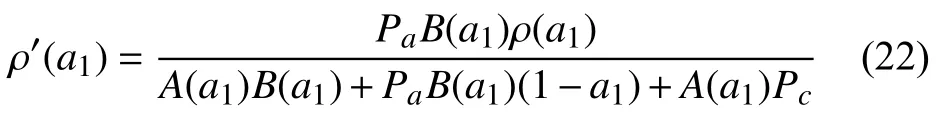
可得ρ′(a1)>0，因此可以得到ρ(a1)为关于 a1的单调递增函数。

由式(22)，可得：

式中，右边分子部分关于 a1单调递增；而分母部分关于 a1单调递减。因此，可得出ρ′(a1)/ρ(a1)为关于a1的单调递增函数。

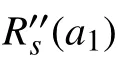
利用上述讨论的结果，可以得出一个能有效解决式(12)的自适应方案。根据不同情况具体讨论步骤如下：

3 仿真结果及分析

图3 对比了几种方案的有效和速率和有效能量效率性能表现。可以看出在绝大部分总功率范围内，本文方案性能表现明显更优。同时，图3 再次验证了非完美信道信息对系统性能造成的严重影响，且对系统的影响程度随着信道不确定程度的增加而增加。

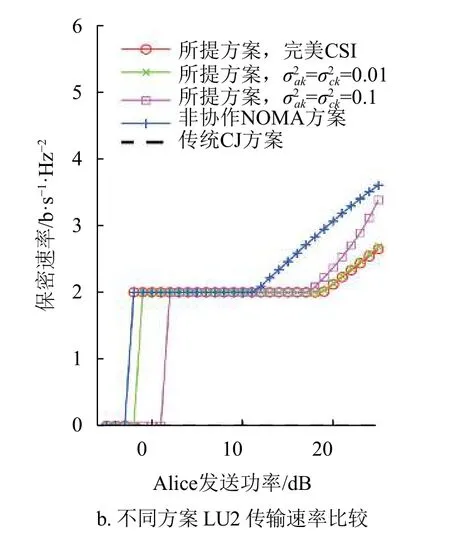
图2 LU1 保密速率和LU2 传输速率性能比较

图3 有效和速率与有效能量效率性能比较

4 结 束 语

本文在非完美信道信息场景中，针对协作NOMA 系统中保密中断概率限制条件下的保密速率最大化问题，提出了一种自适应功率分配算法。仿真结果验证了本方案能有效灵活地提高系统安全性能和能效，具有环境适应性。同时，仿真结果表明，非完美信道信息会导致严重的系统安全性能以及能效下降，如何应对非完美信道信息对协作NOMA 系统带来的影响有待进一步研究。