豪华邮轮多航速兴波阻力的船型优化

刘鑫旺，万德成*

1 上海交通大学 船舶海洋与建筑工程学院，上海 200240

2 上海交通大学 海洋工程国家重点实验室，上海 200240

3 上海交通大学 船海计算水动力学研究中心，上海 200240

0 引 言

近20 年来，我国船舶工业取得了日新月异的发展，造船技术水平不断提高，已成功设计和建造了大量除豪华邮轮外所有类型的船舶。豪华邮轮因其个性化的内装设计、陆地化的层次布局和多样化的娱乐设施，被赋予了“海上移动城市”之美誉，是国际造船业公认的集高技术、高附加值和高可靠性于一身的“三高”船舶，导致其设计建造难度大、造价高。许多发达国家造船业的重心已在向豪华邮轮倾斜，欧洲一些国家凭借其技术、经验和设备供应等方面的优势，在豪华邮轮的设计与建造领域一直保持着领先地位。

2018 年11 月6 日，中国船舶工业集团有限公司与美国嘉年华集团、意大利芬坎蒂尼集团正式签订了13.5 万总吨的Vista 型邮轮建造合同，标志着中国首艘具有世界先进水平的大型邮轮进入实质性建造阶段，为我国自主开展豪华邮轮的设计与建造提供了基础。

与常规船舶相比，豪华邮轮的结构通常具有以下特点：

1） 主尺度：型宽较大而型深较小，方形系数较小，水线以下尖瘦；

2） 艏艉结构：为方艉和弯鼻型球艏，艏柱前倾且有外飘；

3） 推进方式：多采用电力驱动，无主机与推进轴系，机舱占用空间较小，振动噪声低；

4） 美学设计：水线以上部分讲究自然美观，上、下结构需直线对齐。

然而，由于豪华邮轮船型的特殊性（例如商用建造模型不易得到），在豪华邮轮的水动力性能，特别是阻力性能优化方面，相关的文献较少[1-3]，所能获取的文献多为针对豪华邮轮航线和布置等方面的优化[4-7]。因此，考虑到豪华邮轮的上述特点，以及我国对其设计建造方面的强烈需求，需进一步开展基于水动力性能的豪华邮轮设计与优化研究。

本文拟基于自主开发的船型优化设计软件OPTShip-SJTU，以某豪华邮轮为原始船型，采用自由变形（free-form deformation，FFD）方法，对船艏、水线、船艉等位置进行局部变形；通过基于Neumann-Michell（NM）势流理论的兴波阻力求解器NMShip-SJTU 进行阻力评估，结合优化算法得到不同航速下兴波阻力系数最优的船型；通过采用经过广泛验证的高精度黏流求解器naoe-FOAMSJTU，对优化船型做进一步的验证。

1 豪华邮轮的特点及其优化设计要求

豪华邮轮不仅是旅游运输工具，更是旅游休闲之处，这就决定了其在安全、舒适、环保节能等方面比一般类型船舶的要求更高。

1） 安全性。基于豪华邮轮大型化的发展以及船上人员众多的考虑，安全方面的问题越来越受到重视。据统计，豪华邮轮事故大多由破损和失火导致。因此，豪华邮轮的设计不仅要满足《国际海上人命安全公约》（SOLAS）[8]的要求，还要满足《安全返港规则》（SRtP）[9]的要求。根据要求，在一定的安全界限内发生火灾或浸水事故时，船舶应能依靠自身动力安全返港。在此过程中，旅客能安全地处于“安全区域”内并能满足基本生活需求；当事故超出安全界限时，重要系统能运行3 h 以保证有序撤离。可见，充足的动力是必需的。从水动力性能的角度考虑，在船舶以某设计航速航行时，若其受到的阻力较小，无疑会节省动力，以备不时之需。

2） 舒适性。豪华邮轮的舒适性主要是通过控制船舶的振动和噪声实现。豪华邮轮因多采用电力驱动，无主机和推进轴系，故机舱产生的振动和噪声较小。此外，水动力噪声也不容忽视，例如船舶以中、高航速航行时兴起的自由表面波在其生成与传播的过程中会产生水动力噪声，从而影响到邮轮的观赏性和舒适性。

3） 环保节能。为了构建“绿色”海洋，现代邮轮均具有“清洁”、“绿色”船级符号。国际海事组织（IMO）近年来相继推出了用于控制CO2排放的船舶能效设计指数（energy efficiency design index，EEDI）等规则，这些规则将在很大程度上影响豪华邮轮的设计。针对船舶的安全、环保、能效及船员的健康防护等，EEDI 提出了更高的要求。对船舶各水动力性能而言，阻力性能无疑对EEDI的影响最大。

因此，对于豪华邮轮的型线设计，针对阻力性能的船舶设计与优化尤其重要。

随着CFD 技术和船舶CAD 技术的发展，可利用基于数值模拟的船型优化设计彻底摆脱传统的船型设计模式。该技术是以船舶一项或多项水动力性能最优作为设计目标，在给定的约束条件和构型设计空间内，通过CFD 数值评估技术和现代最优化技术来实现船舶水动力构型的优化求解，最终获得给定条件下水动力性能最优的船型。

在基于水动力性能的豪华邮轮型线优化过程中，至关重要的一环是水动力性能评估。根据流体力学中对流体黏性处理方法的不同，水动力性能的评估方法可分为2 大类：基于无黏假设的势流方法和考虑流体黏性的黏流方法。势流方法虽然假设流体无黏，与实际有一定的差异，但对某些特定条件下的问题，例如利用摩擦阻力与兴波阻力叠加代替船舶总阻力，此方法在船舶设计领域仍被广泛采用，并且其最大的优势是在维持较高精度的前提下计算时间与资源消耗极少，可见该方法非常适用于豪华邮轮的初步设计与优化阶段。而考虑黏性的全流场CFD 方法可以更加真实地还原流场情况，方便获取流场所有信息，且具有较高的精度和可信度，可以辅助或在某种程度上替代昂贵的船模试验，但相比势流方法，黏流方法的计算时间和资源消耗巨大。

国内外在船型优化与应用方面已取得巨大进展[10-15]：优化船型从简单的数学船型、标模过渡到实际应用船型；船型变换方法多样；目标函数大多为兴波阻力、总阻力、船艉伴流均匀度等；水动力性能评估方法主要包括经验公式、势流方法、黏流RANS 方法等；优化算法包含基于梯度的优化算法和基于生物进化的智能优化算法等；近似模型主要为Kriging、神经网络等。然而，国内大多是借助商用软件来构建优化平台或评估水动力性能。因此，根据豪华邮轮型线优化的需要，自主开发优化平台，进行基于船舶水动力性能的型线优化迫在眉睫。

对豪华邮轮的阻力优化可通过势流理论方法来高效评估兴波阻力，所得优化船型的兴波阻力可显著降低，进而减小豪华邮轮的总阻力。同时，其还将减小船舶的自由表面兴波进而降低水动力噪声，提高观赏性和舒适性。此外，由于豪华邮轮在使用上的特殊性，其不像一般船舶那样需要根据设计航速来设计建造，而应考虑邮轮上游客的观赏需要。例如，当欣赏优美的海上风光以及海底生物时，需要以较低的航速航行，反之，则需略微提高航速以节省更多时间。因此，在豪华邮轮的设计建造过程中，不能只针对单一航速，而要进行多航速下的性能优化。

本文拟首先采用OPTShip-SJTU 软件，对某豪华邮轮在2 个航速（Fr = 0.171 15和0.209 18）下的兴波阻力系数进行优化，然后采用FFD 方法进行船型变换，阻力性能则由兴波阻力求解器NMShip-SJTU 进行评估，最后采用多目标遗传算法得到优化船型，并进行基于黏流的CFD 评估以验证优化结果的可靠性，以为同类型豪华邮轮的优化设计提供参考。

2 船型优化软件模块与原理

上海交通大学船海计算水动力学研究中心（CMHL）基于C++语言与OpenFOAM 开源平台，自主开发了一款船型优化设计工具OPTShip-SJTU，该软件不依赖其他商用软件，集成了船型变换模块、水动力性能评估模块、近似模型构建模块和优化求解模块，可实现船型的自动优化设计。软件框架如如图1 所示。

图1 船型优化软件OPTShip-SJTU 框架Fig. 1 Framework of OPTShip-SJTU hull form optimization software

2.1 船型变换模块

Sederberg 和Parry[16]最早提出了FFD 方法，该方法类似于弹性物体外壳受到外力变形时，嵌入在其中的几何实体也随之变形。运用FFD 方法，按类似的步骤对三维实体进行变形：首先，将待变形区域用一控制体包围，这相当于将变形物体嵌入到弹性控制体中；然后，通过移动控制体的控制顶点改变控制体形状，该步骤相当于弹性体受到外力而发生变形；最后，处于控制体中的待变形物体随着控制顶点的移动而发生相应的变形。图2 所示为FFD方法示意图。其中图2（a）中黄色的顶点构成初始控制体，图2（b）中粉色的顶点及黄色的顶点分别代表移动控制点和固定控制点。通过该操作，可实现船体艏部的变形。

FFD 方法的控制体一般可选取为长方体，在其长、宽、高三个方向上分别均匀分布(l+1)，(m+1)，(n+1)个控制点，用其将待变形区域包围。控制体内待变形物体的坐标包含全局坐标（O-XYZ）和局部坐标（O'-STU），如图3 所示。

图2 FFD 方法示意图Fig. 2 Schematic diagram of FFD method

图3 FFD 方法的全局坐标与局部坐标系示意图Fig. 3 Schematic diagram of global and local coordinate systems of FFD method

通过下式的函数关系，将控制体内待变形物体的全局坐标与控制顶点的全局坐标建立联系：

式中：Qi,j,k为控制顶点的全局坐标；X 为控制体内待变形物体的全局坐标；（s，t，u）为控制体内待变形物体的局部坐标；Bi,l，Bj,m，Bk,n分别为l，m，n 次Bernstein 多项式。以求和号下的第1 项 Bi,l(s)为例，Bernstein 多项式定义为

由式（1）可看出，全局坐标用于描述物体的空间几何位置，可表示为控制顶点与Bernstein 多项式乘积的线性叠加，因此移动控制顶点时，待变形物体的全局坐标也会发生改变；而局部坐标则表示控制体内待变形物体与控制体顶点的相对位置，一旦控制体给定，控制体内待变形物体的局部坐标（s，t，u）就已确定，变形过程中也不会发生改变。

如果控制体为规则的长方体，且控制顶点在3 个方向均匀分布，则可采用式（3）快速求解局部坐标：

式中：X0为控制体原点的全局坐标；S，T，U 分别为控制体长、宽、高方向上的矢量，如图3 所示。任意一点的局部坐标（s，t，u）都可以通过式（4）求得：

控制体顶点的全局坐标可按式（5）求得：

式中： i=0,1,...,l; j=0,1,...,m; k=0,1,...,n。

本文计算模型是根据初始图形交换规范（initial graphics exchange specification，IGES）文件转换成船体面网格，然后利用FFD 方法进行船型变换而得。当移动FFD 方法中的控制体顶点时，将上述计算得到的局部坐标（s，t，u）以及新的控制顶点坐标代入式（1），即可得到控制体内任意一点变形后的全局坐标。

2.2 水动力性能评估模块

采用NM 方法求解船舶兴波问题。该方法由Noblesse 等[17]于2013 年提出，是对Neumann-Kelvin（NK）理论进行改进而得到的一种方法。在NK 理论中，流场任意一点的速度势都可以表示为船体湿表面积分与沿船体水线积分之和。其中，沿船体水线积分是求解难点，因为需要考虑自由面影响并计算速度势偏导数。NM 理论则引入了协调流动模型和波浪函数，其通过一系列的数学变换，消去了NK 理论中沿船舶水线的积分项。在NM 理论中，只需计算船体湿表面上的积分，就可以得到流场内任意点的速度势。图4 所示为NM 理论坐标示意图。

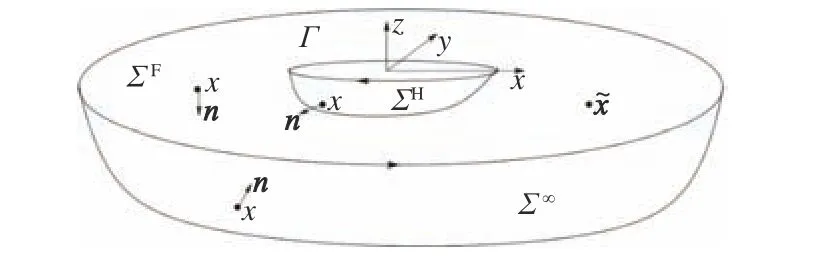
图4 NM 理论坐标示意图Fig. 4 Schematic diagram of coordinate system of NM theory

NM 理论是基于格林函数法来求解速度势，是将边值问题转化为积分问题进行求解。根据格林函数第二公式，可得边界积分表达式

进一步地，根据协调线性流动模型，式（10）经数学推导，可进一步简化为

利用上述公式，可进一步对船舶静水兴波阻力、升沉、纵倾以及自由面波高等进行预报。采用该方法不仅能准确预报船舶阻力变化趋势，而且计算耗时短、空间少，非常适用于船型优化。因此，本文将采用基于上述方法和利用C++语言自主开发的兴波阻力求解器NMShip-SJTU 来作为兴波阻力数值计算的工具。

2.3 响应函数近似模型构建模块

采用上述船舶水动力势流理论和船型设计数值计算量较大，而在船型设计中引入试验设计方法则可在保证一定精度的前提下大幅提高优化效率。

试验设计（DoE）方法是一种从数理统计学的角度确定试验设计方案的方法，其可在保证样本群体精度的同时降低设计方案样本数。图5 所示为以x1，x2为设计变量的均匀分布试验设计、随机拉丁超立方试验设计和优化拉丁超立方试验设计。从中可以看出，优化拉丁超立方试验设计的均匀性和正交性更优，可以更好地提高计算效率。因此，本文采用优化拉丁超立方试验设计方法选取新船型方案样本。

图5 不同试验设计方法的均匀性和正交性示意图Fig. 5 Schematic diagram of uniformity and orthogonality of different DoE methods

Kriging 近似模型[15]是地质统计学建立的近似函数的主要模型，最初主要用于采矿领域，随后被逐渐用于多个领域。该模型是一种针对变量的空间相关性，对变量取值进行无偏、最优估计的方法。其基本思想是：未知点的值是其周围临近点值的平均，权值为与未知点的距离。从插值角度而言，是对空间分布的数据求线性最优、无偏内插估计的一种方法。Kriging 模型具有较好的适应性，可广泛应用于对低阶和高阶非线性函数的逼近。对试验设计中选取的新船型兴波阻力逐一计算后，根据Kriging 近似模型，即可建立表示兴波阻力系数等水动力参数与船型参数之间关系的响应函数，本文将该响应函数用于船型优化。

2.4 优化求解模块

当只有一个目标函数时，可以找到一个全局最优解，该解要优于其他解。而当多个目标共存时，目标之间往往会存在冲突，很难找到一个解来使所有目标同时最优。因此，有一种多目标优化方法，其实质是：在不让任何一个目标变差的前提下，至少使一个目标变优，这种多目标优化方法称为基于Pareto 前沿的优化。对于多目标优化问题，通常存在一个解集，特点是其中所有的解都不再拥有Pareto 优化的余地，这种解集称作Pareto 最优解集。

非支配排序遗传算法（non-dominated sorting genetic algorithm，NSGA）[18]采用非支配分层方法，可以使性能更优的个体有更大的概率存活，其适应度共享策略可防止“超级个体”过度繁殖而早熟收敛。但是，NSGA 仍存在缺乏精英策略、计算复杂等问题。NSGA-II 引进了精英策略，将优良的父代个体直接保存到子代种群，能防止因优良个体丢失而导致的算法效率下降；另外，采用拥挤度比较算子来评估个体周围的群体密度，并同时根据非支配排序和拥挤度选取合适的个体，在含精英策略的条件下可保证种群的多样性。因此，NSGA-II 成为目前最流行、最可靠的多目标遗传算法之一，也是本文采用的多目标兴波阻力优化算法。

3 豪华邮轮型线优化实例

3.1 优化问题的建立与求解

本文针对首个国产的13.5 万吨级Vista 型豪华邮轮在2 个航速（Fr=0.171 15 或0.209 18）下的兴波阻力进行了优化设计，船体形状和主尺度分别如图6 和表1 所示。

图6 豪华邮轮外形主视图Fig. 6 Main view of luxury cruise ship

表1 豪华邮轮主尺度Table 1 Main dimensions of luxury cruise ship

优化时，需精心考虑几何重构区域，以便对船舶兴波阻力产生影响。考虑到局部变形范围限制对整船湿面积大小的影响不大，以兴波阻力代表总阻力来对目标进行船型优化。选取2 个航速下的兴波阻力系数Cw作为目标函数，按上节所述原理对其进行多目标优化，目标函数定义为：

采用FFD 方法对船艏、艉进行几何重构，如图7所示。图中3 个长方体框分别代表3 个FFD 变形区域，红色线条为水线。下面，将予以详细说明。

图7 豪华邮轮FFD 变形框示意图Fig. 7 Schematic diagram of FFD lattices of luxury cruise ship

首先，因豪华邮轮的弯鼻球鼻艏可以降低兴波阻力，故可以优化其形状，在球艏区域设置一控制体，实现球艏在长度、宽度和高度上的变化。但由于该豪华邮轮吃水较浅，导致球艏有一小部分在水面上，为确保主尺度中的水线长不变，需要限制球艏处的进水点不变，这就要求该变形框在沿船长及吃水方向的控制点要有所限制，以防止进水点在船长方向上的变化，以及由于吃水方向的变形导致原进水点进入水下而使水线面变小。

其次，虽然进水点限制不变，但因入流段水线宽可以变值，即整个艏部水线（平行于舯体前）都可以在船宽方向上发生变化，因此可在近水线处设置变形框，但要保证型宽不变。

最后，在船艉去流段（平行于舯体后）设置变形框，按吃水方向移动近水线的控制点及2 个横剖面在船宽方向的控制点来综合改变艉部横剖线的UV 度。

各控制体内均匀分布了控制顶点。图8 中，绿色控制点为固定控制点，红色控制点为移动控制点，设计变量总数为7 个，如表2 所示。表中，7 个设计变量的变化范围为无因次化位移。

采用优化拉丁超立方试验设计方法，在由7 个设计变量所形成的样本空间中生成均匀、正交的样本点，总计280 个，不同设计变量在设计空间中的分布如图9 所示。同时，通过FFD 方法变形得到280 个新船型，之后评估各新船型的兴波阻力，最终，采用Kriging 模型构建近似响应函数曲面来代表目标函数与设计变量间之的关系。

图8 船体各变形框FFD 控制顶点分布Fig. 8 Distribution of control points of FFD lattices

表2 优化算例定义Table 2 Definition of optimization case

图9 不同设计变量在设计空间中的分布Fig. 9 Distribution of different design variables in design space

3.2 优化结果与分析

图10 兴波阻力系数Pareto 前沿Fig. 10 Pareto front of wave-making drag coefficient

采用多目标遗传算法NSGA-II 搜索最优解，初始群体大小为200，交叉率0.8，变异率0.2，最大迭代次数400，最终获得Pareto 前沿如图10 所示。图中，fobj1和fobj2分别为较低航速和较高航速的兴波阻力系数值，蓝色的星点构成优化算法获得Pareto 前沿。从中可以看出，与单目标优化问题相比，多目标优化不再是寻求唯一最优解，而是一系列可行解的集合。Pareto 前沿形成了一个凸集，即相比Pareto 解，其不存在其他解，使得目标函数f1减小的同时f2也减小，或者f2减少的同时f1也减小。另外还可以看出，最优前沿的各优化船型在Fr=0.171 15 和0.209 18 时其兴波阻力系数为负相关。本文选取Pareto 解集上的2 个可行解（OPT1 和OPT2），如表3 所示，对优化结果进一步进行分析与验证。

图11 所示为2 个优化船型与原始船型的横剖线对比图。从中可以看出，球艏部分与船艉部分变形的差异较大，入流段水线变化基本一致。

基于NM 理论，对比2 个优化船型（OPT1, OPT2）与原始船型的自由面兴波，结果如图12 所示。从中可以看出，由于球艏变形，导致优化船型在2 个航速下其船艏波的波峰和波谷均有所降低，其中OPT1 的优化效果更明显。

为进一步验证优化结果的可靠性，对原始船型和2 个优化船型分别在2 个航速下的静水总阻力进行了评估，求解器采用基于OpenFOAM 平台自主开发的黏性流动求解器naoe-FOAM-SJTU[19-20]。该求解器包含六自由度运动模块和数值造波模块，可以准确预报快速性、耐波性、推进性和操纵性等船舶水动力性能，并能给出精细的流场特征，其可靠性已在很多研究中[19-20]得到验证。

表3 优化船型设计变量取值Table 3 Design variable values of optimal hulls

图11 优化船型与原始船型型线对比Fig. 11 Comparison of hull lines between optimal and initial hulls

图12 势流评估下优化船型与原始船型自由面兴波对比Fig. 12 Comparison of wave elevation between optimal and initial hulls by NMShip-SJTU

基于naoe-FOAM-SJTU 求解器，得到2 个优化船型与原始船型的自由面兴波z、船体表面压力p 分布对比如图13 所示。从中可以看出：OPT1在船艏位置兴波有所降低，艏部高压区略降低；OPT2 主要在船的平行舯体位置兴波有所降低，艏部高压区降低明显。

表4 和表5 所示分别为2 个优化船型与原始船型总阻力评估结果的对比。由表可见，基于势流评估下得到的优化船型，其总阻力中的压阻力均明显下降，说明基于NM 理论评估得到的优化船型可靠；而在摩擦阻力几乎不变的情况下，总阻力均较原始船型有所降低。实际上，本文利用势流理论求解器时并未考虑黏性的影响，因此优化目标为不同航速下的兴波阻力，从兴波阻力的优化效果来看，优化幅度较大。与兴波阻力对应的是黏流求解器求得的总阻力中的压阻力成分，由压阻力结果也可见其从侧面反映出了基于势流的优化效果。后续进行验证时，可补充模型试验验证或其他商用软件验证来进一步说明本文方法的可靠性。上述结果表明，基于NM 理论的兴波阻力优化可以得到总阻力性能更优的船型，相比基于黏流的CFD 评估，其优化更高效，具有较高的应用价值。

图13 黏流评估下优化船型与原始船型自由面兴波、船体表面压力分布对比Fig. 13 Comparison of wave elevation and hull surface pressure distribution between optimal and initial hulls by naoe-FOAM-SJTU

表4 原始船型与OPT1 优化船型的总阻力对比（Fr = 0.171 15）Table 4 Comparison of total resistance between initial and OPT1 hulls at Fr = 0.171 15

表5 原始船型与OPT2 优化船型的总阻力对比（Fr = 0.209 18）Table 5 Comparison of total resistance between initial and OPT2 hulls at Fr = 0.209 18

4 结 语

本文采用船型优化软件OPTShip-SJTU，对某豪华邮轮的阻力性能进行了优化。首先，结合豪华邮轮的特点和设计要求，分析了对船体进行合理变形来得到新船型的方法；然后，利用优化拉丁超立方试验设计的结果，对各新船型采用NMShip-SJTU 求解器进行了兴波阻力系数的计算；最后，通过建立的近似响应函数模型，利用NSGAII 优化算法对豪华邮轮在2 个航速下的多目标兴波阻力系数进行优化并予以了进一步的验证。结果表明，基于势流理论评估对船舶静水兴波阻力性能进行优化的方法高效，其结果可采用黏流评估的结果予以验证；OPTShip-SJTU 可广泛应用于豪华邮轮实用船型的阻力性能优化，2 个计算航速下的总阻力减阻效果分别达0.65%和0.98%。基于豪华邮轮的实际需求和特点，后续还可考虑针对其上层建筑高、稳性差的稳性优化，针对美学需求的豪华邮轮外形主尺度优化，以及针对游客舒适性、方便游览、防止晕船的耐波性优化等。