Scratch趣味数学

古诗中不仅有山水人物家国情怀，还有数学题呢，它是古算家智慧的光芒，在感受古诗词的美的同时也体会到了数学的奥妙，启迪我们的心智。用编程解决这样的古算诗题会更容易更有趣。本章我们将学习用编程解决数学里的一元一次方程和二元一次方程。

所谓一元一次方程，就是在含有未知数的等式中，未知数的种数有一种，并且未知数的最高次方为一次。所谓二元一次方程，就是在含有未知数的等式中，未知数的种数有两种，并且未知数的最高次方为一次。

一、牧童分杏問题

牧童分杏

牧童分杏各竞争，不知人数不知杏;

三人五个多十枚，四人八枚两个剩。

牧童和杏各几何？

1. 题意分析：有一群牧童争着分杏，如果按照每3个人分5个杏子就会剩下10个，但是按照每4个人分8个杏子就会剩下2个，请问牧童有多少人？有多少杏子？

2. 题意转换：由于保持恒定不变的是杏子的总数，所以假设牧童的个数为X，则可以通过两个含有未知数的式子算出杏子的个数：5个杏子分给3个人，一人分5/3个，剩余10个;第二种，8个杏子分给4个人，一人分8/4个，剩余2个。

3. 数学求解

5/3*X+10=8/4*X+2;

5/3*X-2*X=-8;

-1/3*X=-8;

X=-8×-3;

X=24;

求解出答案，牧童人数为24，得出杏子总数为8/4*24+2=50个。

4. 程序推理

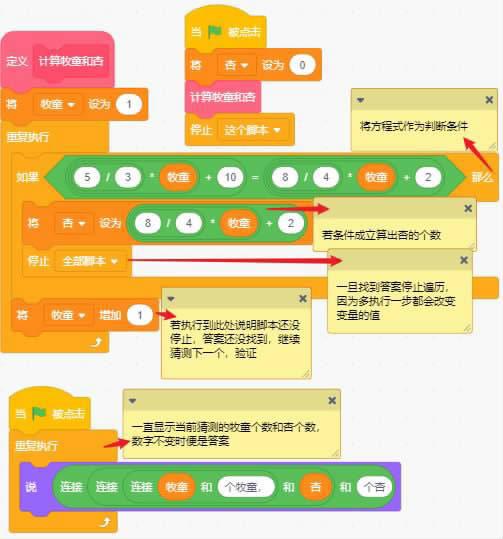
用程序解方程和数学求解思路并不相同，一般用例举方程所有可能解的方法——枚举法。当一个问题有有限种解的情况，我们将这个有限种情况一一列举，并加以验证，枚举的极限情况就是完全归纳法（找出了所有可能情况进行验证）。枚举这是一种朴素的思维方法，却有着强有力的逻辑内涵，同时也切实有效，与计算机的高速运算能力极其相配。

先假设牧童有1个（X=1），判断5/3*X+10=8/4*X+2条件是否成立，若成立则找到答案，若不成立，假设牧童有2个（牧童增加1），判断5/3*X+10=8/4*X+2条件是否成立，若成立则找到答案，若不成立……以此类推求出答案。这样将变量的所有可能的取值依次去检验的算法就是枚举算法，我们在用程序求解方程的解的时候枚举算法是经常被采用的方法之一。

运用循环和变量就可以实现枚举求解，程序如下图。

二、 二元一次方程通用解法

二元一次方程，就是含有两个未知数，并且未知数的最高次方为一次的整式方程。所有二元一次方程都可化为aX+bY+c=0（a、b≠0）的一般式与ax+by=c（a、b≠0）的标准式，例如我们常见的鸡兔同笼问题。

一个二元一次方程通常可以如此表示：

经过求解可得求根公式：

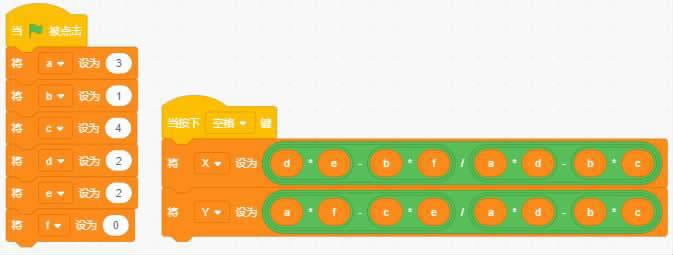
有了这个公式，我们用程序将公式表达出来，计算时输入abcdef的值就可让程序帮忙计算了。

比如一个方程：

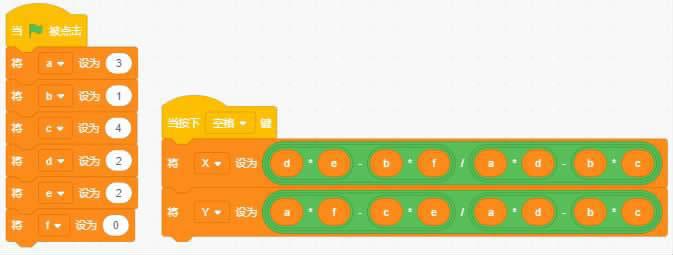
那么依次填入a=3，b=1，c=4，d=2，e=2，f=0，按空格就可以计算出x=2，y=-4。