基于改进极限学习机的焦煤惰质组分类方法

王培珍，刘 曼，王 高，张代林

(1.安徽工业大学 电气与信息工程学院，安徽 马鞍山 243032; 2.安徽工业大学 煤的洁净转化与综合利用安徽省重点实验室,安徽 马鞍山 243032; 3.安徽工业大学 冶金减排与资源综合利用教育部重点实验室,安徽 马鞍山 243032)

焦煤是炼焦的主要优质原料，其显微组分的构成与焦煤的结焦性、黏接性、对CO的吸附能力、热破碎性等密切相关，直接关系到所炼焦炭的质量及其在转化过程中的高效利用[1-2]。目前国内外对于煤岩显微组分的分类与识别，普遍采用的是数点法，该方法自动化程度低，其结果受人为因素的影响较大。因此，利用模式识别的方法对焦煤显微组分进行自动分类与识别对焦煤资源的合理利用、优化配煤结构具有重要意义。

近年来，已有学者采用人工神经网络(Artificial Neural Network，ANN)[3-4]、支持向量机(Support vector machine，SVM)[5-6]等方法尝试对煤矿开采中煤岩界面的煤与矸石进行识别，取得了一定效果。然而，神经网络用于分类时，需要大量的训练样本，且易于陷入局部最优。针对煤岩显微组分结构复杂且样本数有限问题，笔者曾尝试采用支持向量机对煤岩显微组分中镜质组与壳质组显微组分进行分类[7-8]，取得了较好的效果。然而，SVM在学习过程中需要通过各种策略确定核函数、误差控制等参数。极限学习机(Extreme Learning Machine，ELM)[9-10]是一类基于前馈神经网络的学习算法，其特点在于其为单隐含层，且输入层和隐含层之间的权值矩阵及隐含层的偏置可以随机初始化，隐含层和输出层间权值矩阵可以通过求解Moore-Penrose广义逆获得，无需通过反向传播算法迭代更新。由于隐含层节点数通常少于训练样本数(或相当)，ELM的计算复杂度较低;从分类器的性能看，即便是在隐含层节点数很少时，ELM亦可获得接近甚至优于SVM的分类效果[11-12]，且具有可在线训练[13]及可与传统的核方法相结合[12]等特性，已在目标快速识别、语音识别等方面取得了成功的应用[14-15]，并引起研究者广泛的兴趣。

鉴于ELM上述特点及良好的泛化性能，笔者将其引入到具有复杂结构的焦煤惰质组显微组分的分类中。由于ELM在通过求解Moore-Penrose广义逆来获取隐含层的输出权值矩阵的过程中，需要预先确定最优的正则系数和最优的隐含层节点数，而这两个参数通常需要通过大量的组合实验才能确定，为此，笔者将奇异值分解(Singular Value Decomposition，SVD)引入到ELM方法中，推导出SVD与Moore-Penrose广义逆的关系，进而利用SVD求解矩阵的Moore-Penrose广义逆，以避免ELM训练中参数选择问题，提高算法的稳健性。

1 极限学习机的改进

1.1 极限学习机

设有N个样本{xi,ti}，i=1,2,…,N。其中:xi∈Rn，n为特征空间的维数;ti∈Rm，ti为样本特征xi对应的类别标签，m为类别数。一个隐含层节点数为L、激活函数为g(x)的单隐含层前馈神经网络可表示为

(1)

式中，βi为隐含层第i个节点与输出神经元相连接的权值;wi为输入神经元与隐含层第i个节点相连接的权值;bi为隐含层第i个节点的偏置;oj为样本j的输出值。

若该前馈神经网络能以零误差逼近所有样本，即

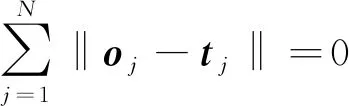
(2)

则存在βi，wi，oj，使得

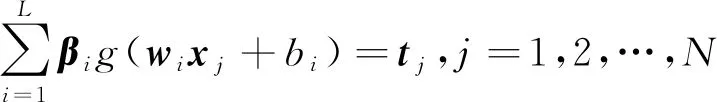
(3)

式(3)可简化为

Hβ=T

(4)

式中，T为由样本类别标签ti构成的矩阵;H为隐含层输出矩阵。

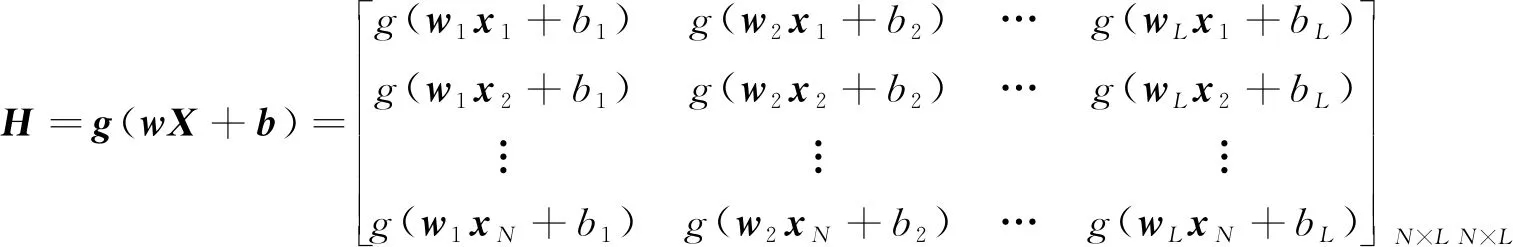
(5)

式中，g，X，b分别为由激活函数g(x)、样本特征xi和隐含层节点偏置bi构成的矩阵。

(6)

若激活函数g(x)无限可微，则输入权值w和隐含层偏置b可随机初始化。输出权值β通过求解式(7)所示方程组的最小二乘解获得

min‖Hβ-T‖

(7)

其解为

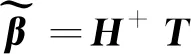
(8)

式中，H+为隐含层输出矩阵H的Moore-Penrose广义逆，其计算方法为

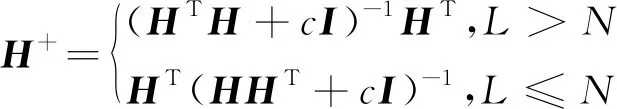
(9)

式中，c为正则化系数;I为单位矩阵。

1.2 基于 SVD的ELM权值矩阵求解

在ELM中输出权值β矩阵的求解需要通过计算隐含层输出矩阵H的Moore-Penrose广义逆矩阵(式(9))。计算过程中，需要确定正则化系数c和隐含层节点数L。通常的方法是采用组合实验的方法确定这2个参数的最优值，需要花费大量的时间及人工参与。为此，笔者引入SVD分解，求解其与Moore-Penrose广义逆的关系，利用SVD分解直接求解矩阵的Moore-Penrose广义逆，对参数矩阵的求解过程进行优化。

定义:设矩阵A∈Cs×n，若存在矩阵G∈Cn×s满足下列关系AGA=A，GAG=G，(AG)H=AG，(GA)H=GA，则称G为A的Moore-Penrose广义逆，记为A+。

根据SVD分解定理，若矩阵A的秩rank(A)=r>0，存在s阶酉矩阵U和n阶酉矩阵V，使得

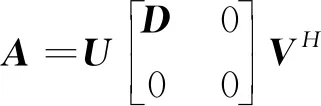
(10)

其中，D=diag(σ1,σ2,…,σn)，且σ1≥σ2≥…≥σn>0，σi为矩阵A的正奇异值。设矩阵

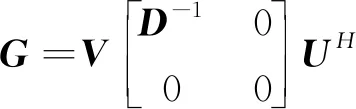
(11)

推导可得

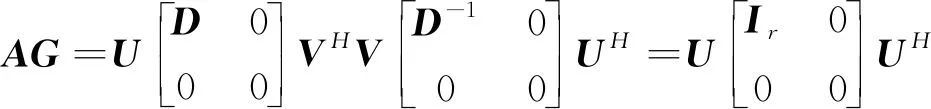
(12)

(13)

(14)

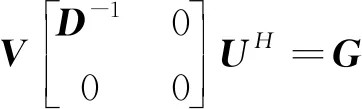
(15)

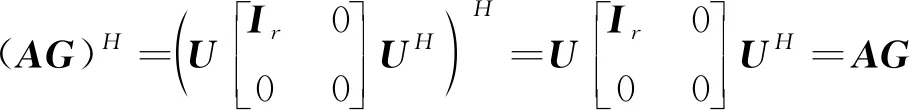
(16)

(17)

式中，Ir为r阶单位矩阵。

由定义知，矩阵G即矩阵A的Moore-Penrose广义逆。

基于上述推导，笔者在ELM输出权值矩阵β的求解中，先对输入权值w和隐含层偏置b进行随机初始化，由式(5)计算隐含层输出矩阵H(相当于矩阵A)，再由式(11)求出其Moore-Penrose广义逆H+，由式(8)得β的解。

2 分类方案

2.1 焦煤惰质组显微组分特点

焦煤是烟煤的一种，其煤化度较高，结焦性好而成为炼焦的最好原料，而惰质组则是影响其结焦性能的重要因素。依据国家标准《烟煤显微组分分类(GB/T 15588—2013)》[16]，惰质组根据细胞结构保存的程度、大小、形态及光性特征可分为丝质体、半丝质体、粗粒体、微粒体、真菌体、分泌体、碎屑惰质体等显微组分，其中丝质体又分氧化丝质体和火焚丝质体，其油镜反光下典型显微图像如图1所示[17]。

图1 典型惰质组显微组分图像

由图1可以看出，惰质组中不同显微组分其亮度、形态上具有各自的特点，且不同组分间存在一定的差异，如:丝质体、粗粒体、分泌体、真菌体呈明亮的颜色，图像中不同区域灰度对比度较大;半丝质体、微粒体整体较暗，灰度对比度较小;粗粒体、真菌体、分泌体呈圆形、椭圆形或环形结构，而火焚丝质体、半丝质呈星状、不规则的条带状结构;氧化丝质体呈筛状结构;微粒体大多数分布于矿物沥青质体中，常呈细小的近圆形颗粒;碎屑惰质体则呈棱角状或不规则形状。

上述分析表明，惰质组不同显微组分其光特性(亮度分布)、形貌特征上存在差异，且具有明显的纹理结构。

2.2 特征量的提取与分类方案的构建

根据上节分析结果，笔者依据惰质组显微组分的光性特征，提取基于灰度统计分布的亮度比、均值、方差、偏度、一致性及峰度等6个特征量;依据其形貌、纹理特征，提取基于灰度共生矩阵的能量、熵、惯性矩、局部平稳性及最大概率等5个特征量，共11维初始特征。特征量的定义见文献[8]。

由于焦煤惰质组各显微组分结构复杂，由主观分析构建的初始特征空间其维数较高;不同显微组分间某些特征(如亮度分布、区域形状)存在相似性[18]，因而特征数据量间存在相关性及冗余，从而影响后续分类的准确性。为了降低特征空间的维数、去除特征数据的冗余，先采用主成分分析法(PCA)[8]对焦煤惰质组各显微组分初始特征量进行抽取，降低特征空间的维数、去除其相关性，再采用本文改进的极限学习机对样本进行分类。

2.3 分类器的训练

极限学习机是一种基于单隐含层的前馈神经网络[9]。经过本文改进后，其训练的主要步骤如下:

(1)对训练样本进行标注，设训练样本为X，对应的类别标签为T。

(2)根据经验，设计初始特征量集，计算训练样本初始特征量;采用PCA对初始特征进行抽取，得到用于分类的特征量集Y。

(3)选择激活函数g(x)，并随机初始化输入权值矩阵w和隐含层偏置矩阵b。

(4)根据式(5)计算隐含层输出矩阵H=g(wY+b)。

(5)用SVD分解对H进行分解，根据式(9)求其Moore-Penrose广义逆H+。

(6)根据式(8)计算ELM的输出权值矩阵β的解。

3 实验及结果分析

实验平台配置为Windows 7 64bit，CPU i7-4700MQ 2.5GHz，6G内存。算法在Visual Studio 2013平台结合OpenCV编程实现。

3.1 实验数据和实验设置

实验用焦煤煤样来源于山西焦煤集团有限公司西山、河东、霍西煤田及河南平顶山煤田、东升煤矿，图像为煤样在油浸反射光下通过光学显微镜获取的焦煤显微图像，400倍放大。由于氧化丝质体与火焚丝质体形貌差异较大，实验中将其作为2类。训练数据样本和测试数据样本均含8类，每类15个，共120个样本。

在ELM中，输入权值矩阵w和隐含层偏置矩阵b的初始化为在[-1,1]上的随机均匀分布，激活函数选择Sigmoid函数。表1为由本文训练样本的11个初始特征量进行PCA后的各主成分(PC1～PC11)对应的本征值及相应的累积贡献率，其中本征值越大，其对应的信息量也越大。可以看出，主成分由PC1至PC7，其累积贡献率[8]已达99.83%，即已包含原始特征中99.83%的信息，因此，取PCA之后的前7个主成分(PC1～PC7)所对应的本征值为降维后的新特征量，即PCA降维后新的特征空间维数取为7。此外，后续图1,2及表2中关于分类结果的数据均为10次实验结果的平均值，其中分类准确率为分类正确的样本数与样本总数的比值(百分比)。分类器所得结果的正确与否由专家鉴定。

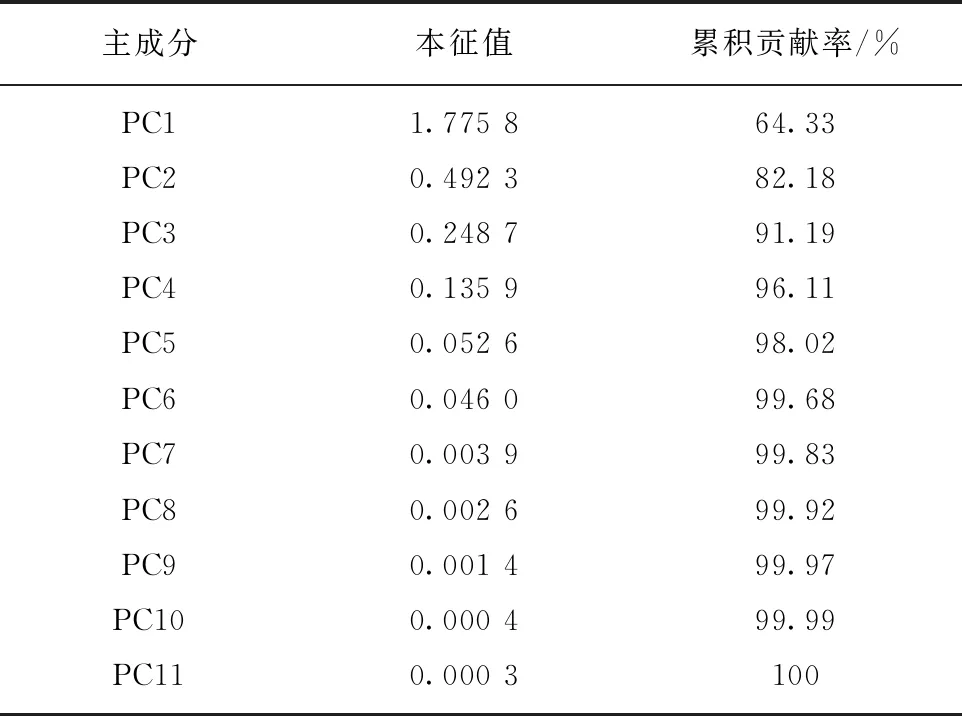
表1 主成分分析结果及累积贡献率

3.2 结果与讨论

3.2.1隐含层节点数对分类结果的影响

为探讨ELM隐含节点数对分类结果的影响，初始化隐含层节点个数为2，逐渐增加节点个数，分析节点数对训练样本和测试样本的分类准确率的影响，结果如图2所示。由图2可以看出，随着隐含层节点数目的增加，对训练样本的分类准确率也逐渐升高，当隐含节点数为15左右时，其分类准确率已达0.98，且在隐含层节点数为65左右时分类准确率趋于1，并稳定于最大值。然而，从对测试样本的分类准确率看，当隐含层节点数由较小的值逐渐增加时，测试样本分类准确率随之上升;但上升至一定程度之后，再增加节点数则呈下降的趋势，并且变得不稳定，亦即对于测试样本来说，并非隐含层节点个数越多越好。出现这一问题的主要原因在于，随着隐含层节点数增加，ELM出现过拟合的现象，导致分类器的泛化能力变弱。因此，在选择隐含层节点数目时，需要综合考虑训练样本和测试样本的分类准确率。

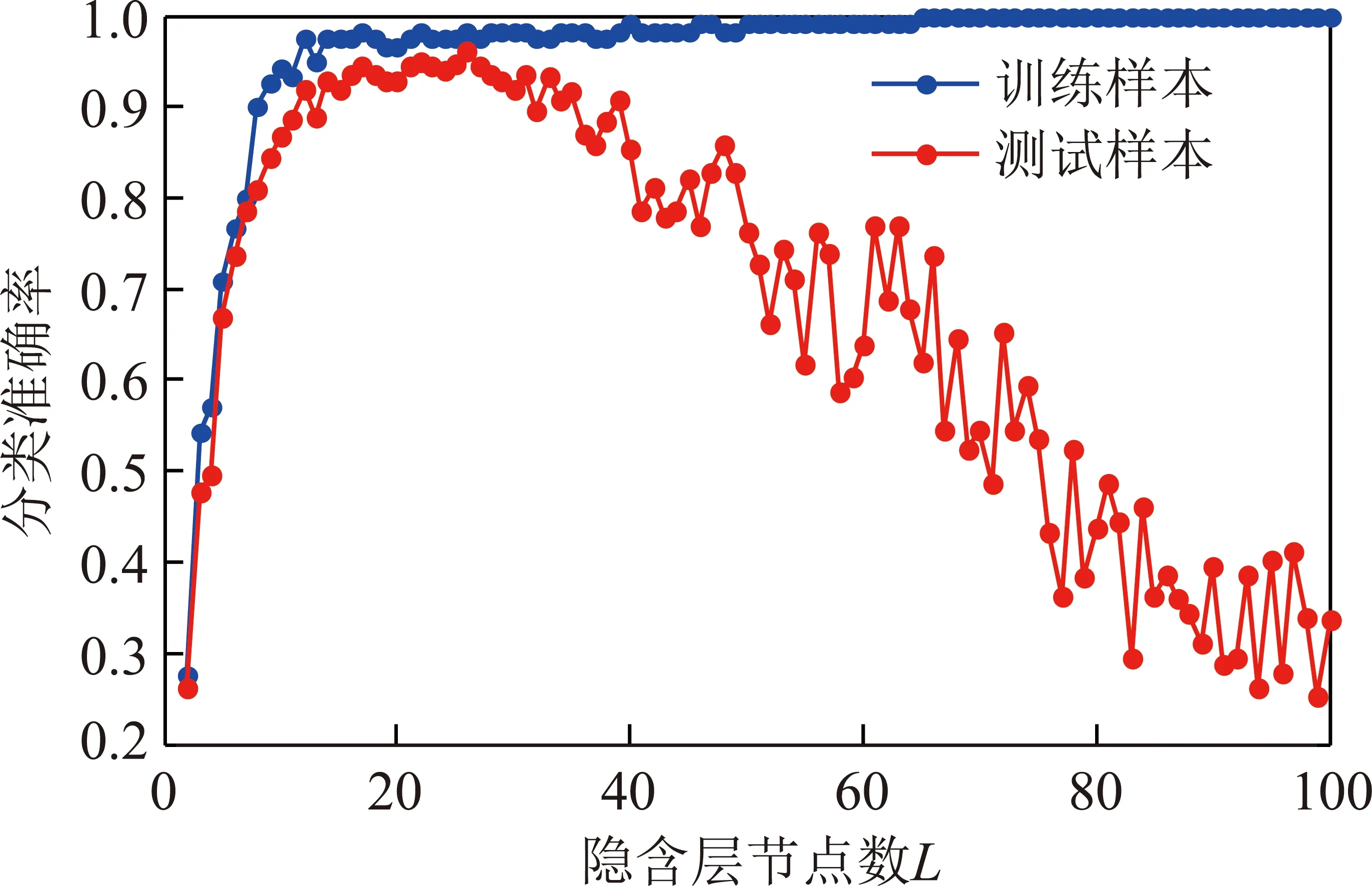
图2 隐含层节点数对ELM分类准确率的影响

3.2.2特征抽取对分类结果的影响

为了验证本文方案中特征抽取对分类结果提升的有效性，分别采用先PCA降维再由ELM分类(本文方案)和用初始特征量直接由ELM分类2种方案对测试样本进行实验，其分类准确率如图3所示。与图2类似，2种方法的分类准确率的变化都随着隐含层节点数目的增加先上升后下降。在隐含层节点增加过程中，本文方案(proposed)分类准确率上升比直接采用ELM快，且比单一ELM先达到最大分类准确率。本文方案在隐含层节点数L=19时达到最大分类准确率，为0.967;单一ELM在L=26时达到最大分类准确率，为0.958。此外，相对于单一ELM分类，本文方案在较宽的范围维持在较高准确率，且准确率在下降过程中波动较为平稳。以上分析结果表明，本文方案中先采用PCA对特征空间进行降维、去相关对于分类准确率的提高有明显效果。

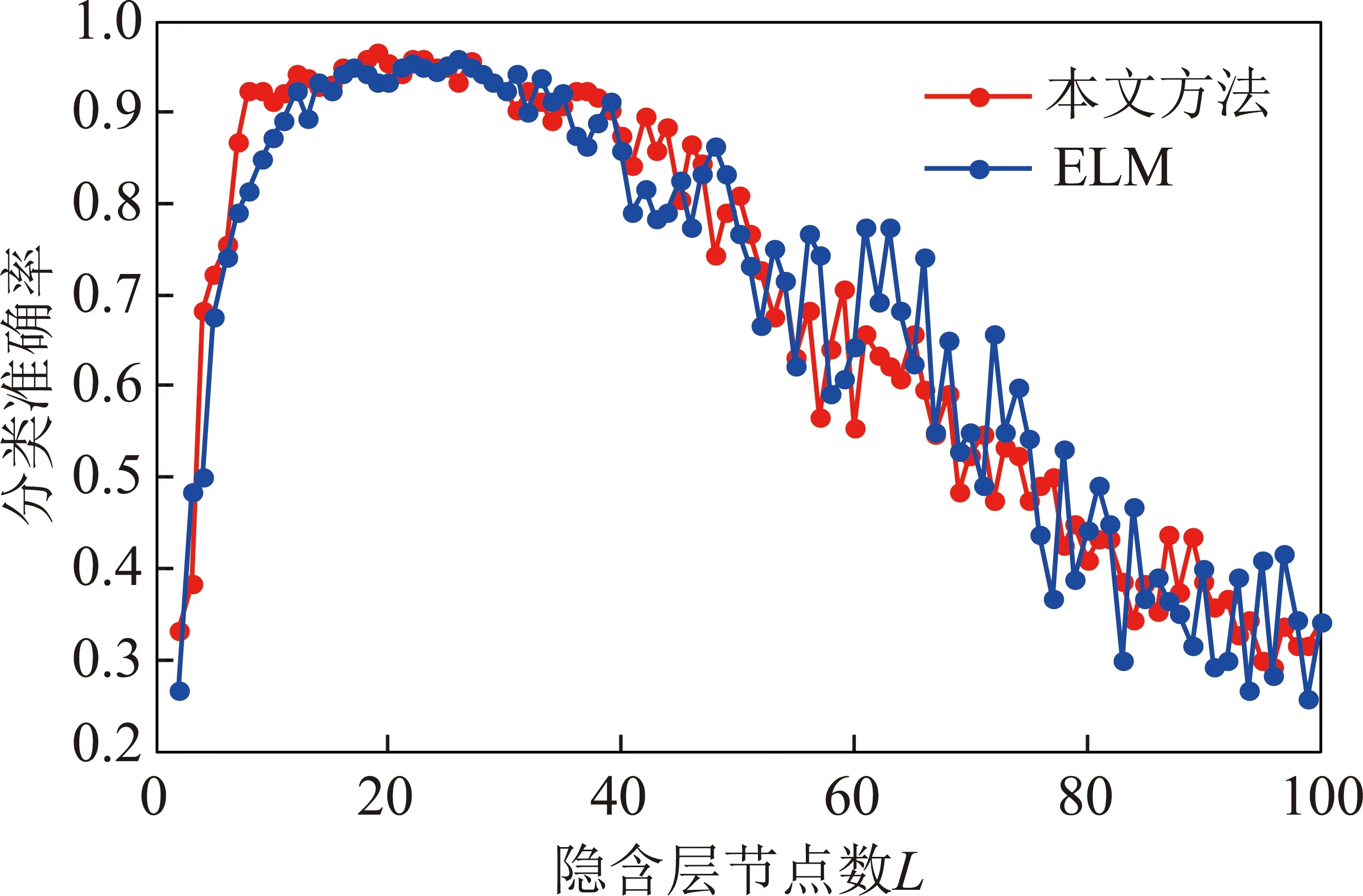
图3 本文方法和单一ELM分类结果对比

根据图3结果，用本文方法对120个测试样本进行分类，隐含层节点数L取19时分类结果如图4所示。8个类别依次为:氧化丝质体、火焚丝质体、半丝质体、粗粒体、真菌体、微粒体、分泌体、碎屑惰质体，标号分别为1～8。图中“·”表示样本的实际所属类别，“+”表示采用本方案分类结果。如果两者重叠，则分类正确，不重合则分类错误。8个类别中，第4类(粗粒体)有1个错分为第7类(分泌体)，第7类有3个错分为第4类，其主要原因在于粗粒体与分泌体在亮度及形貌上均存在较大的相似性。

图4 测试样本分类结果

3.2.3不同分类方法结果比较

为分析本文方法对焦煤惰质组分类问题的适应性，建立同样适合于小样本问题的支持向量机(SVM)分类模型，其中核函数选为径向基函数(RBF)，惩罚因子C和核函数参数g采用交叉验证选择，通过训练得最优参数C=1.0，g=0.506 25。SVM,ELM和本文方法的分类结果见表2。

表2 不同方法的性能比较

从分类准确率来看，本文方法虽然对于训练样本没有达到100%的准确率，但对于训练样本，其分两类的准确率可达96.7%，明显高于SVM，且比单一ELM已有所提高;从分类性能来看，相对于SVM，单一ELM及本文方法均可以较少节点数获得与SVM相近的分类能力(本文方案19个节点，ELM使用26个隐含层节点，SVM使用74个支持向量)，且对于测试样本，采用本文方法及单一ELM两种方法其分类准确分别高出SVM4.2%和3.3%，表明ELM方法具有更高的泛化能力。从消耗时间来看，由于ELM需要通过组合实验预先确定最优的正则系数和最优的隐含层节点数，SVM需要通过交叉验证进行参数调整，训练耗时大为减少，改进的ELM不需要调整网络的输入权值以及隐含层的偏置，其训练时间大为缩短，约为SVM的1/5。由于本文方法在ELM的基础上先用PCA对原数据进行抽取，消除数据的相关冗余、降低特征维数，相对ELM训练时间减少约60%，测试时间也有所减少，隐含层节点数减少近40%，分类效率得以提高。

综上所述，本文方法较之于ELM和SVM其总体性能均有明显提高。

4 结 论

(1)在ELM输出权值矩阵β的求解中，利用SVD求解隐含层输出矩阵广义逆，避免了分类器训练中参数选择所要进行的大量实验，提高了算法的稳健性和学习机的智能化程度。

(2)通过PCA提取特征信息，去除了特征量间的相关性及数据冗余，降低特征空间维数，提高了分类的准确率。

(3)与其它方法的对比，本文方法分类的准确性、泛化能力、训练效率等方面均有明显提高，对于训练样本的分类准确率可达96.7%。

此外，本文方法可推广至煤岩其他类别显微组分的分类与识别中。