一种基于卡西斯基试验的密钥破译算法分析

◆杨振 杨帆 夏山 高钏淏 万贺

一种基于卡西斯基试验的密钥破译算法分析

◆杨振 杨帆 夏山 高钏淏 万贺

（成都信息工程大学网络空间安全学院 四川 610200）

卡西斯基试验（Kasiski examination）是弗里德里希·卡西斯基于1863年提出的针对维吉尼亚密码的破译方法，它通过在密文中搜索长度大于3的相同密文序列并计算几者之间相隔的字母个数来推测密钥的长度。且维吉尼亚算法对密钥的简单填充处理使得它易于破解，对后世提出“完善保密性”也产生了一定影响。本文的算法基于卡西斯基试验，通过循环移位法确定密钥长度。随机模拟实验表明，它可以简单、高效、准确地提取对密钥进行了错误填充的流密码的密钥长度。

维吉尼亚密码；异或；密钥长度

维吉尼亚密码算法曾多次被发明，以其简单易用而著称。弗里德里希·卡西斯基于1863年提出，在未知维吉尼亚密码密钥长度的情况下可以用卡西斯基试验法猜测密钥长度。一旦确定了密钥长度，密文就可以用矩阵形式排列，对于每一列便可以使用频率分析攻击推测出对应的明文和密钥，由此来实现对维吉尼亚密码的破解[1-2]。本文主要分析一种基于卡西斯基试验的更为简单高效的算法，通过对维吉尼亚加密和异或流密码加密的测试发现，该算法对于确定多表替换密码密钥长度的效果良好。

1 简介

1.1 维吉尼亚加密算法

维吉尼亚算法的明文空间、密钥空间、密文空间均为26个英文字母。

算法首先将明文和密钥中的字母依据其在字母表中的顺序将字母和数字做一个映射，比如a对应0、b对应1......

然后将密钥重复复制，填充到和明文一样的位数，再对明文进行逐位加密。加密和解密的算法可以用以下的同余式表示[3]：

加密：

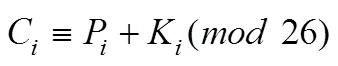
解密：

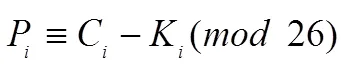
1.2 流密码

流密码是一种对称加密算法。它要求加密者和解密者使用同样的数据流作为密钥，明文数据流和密钥数据流顺次对应加密，得到密文数据流。

OTP（one-time pad，一次性密码本）密码是一种流加密算法，加密和解密算法可以描述为：

加密：

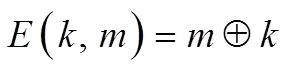
解密：

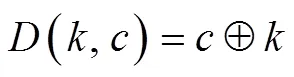
其中密钥和明文的长度相同，是真正随机产生的且只使用一次。

虽然OTP密码的加解密处理只是做了一个简单的异或运算，但在理论上，克劳德·艾尔伍德·香农已经证明该算法是绝对安全的[4]。3.1节将进一步讨论OTP密码。

1.3 卡希斯基试验

举一个简单的维吉尼亚加密的例子，明文为say to me that you love me forever tomorrow morning，密钥为sky，则：

明文：saytomethatyoulovemeforevertomorrowmorning

密钥：skyskyskyskyskyskyskyskyskyskyskyskyskysky

密文：kkwlykwdfsdwgejgfceodgbcnoplykgbpggkgblaxe

可以看到密文中有用粗体标记的重复kgb序列，这是因为在明文中有mor的重复序列，并且他们间隔的字母个数恰好是密钥长度的倍数，即6。因此我们可以在密文中寻找一定长度的重复序列，并且计算他们之间间隔的字母个数，经过多次计算后取这些字母个数的最大公因数，就能基本推测出密钥长度了。

比如，我们还能在密文中发现重复的lyk序列，这两个重复序列的间隔数是24，kgb重复序列的间隔数是6，则可以假设密钥长度为gcd（24，6）=6，虽然结果是实际密钥长度的2倍，但其对后续密文的破解操作影响不大。

值得注意的是，密文中其实还有一个重复的kw序列，但他们间隔的位数是4，如果以kw序列和kgb序列作为数据计算的话，则会得到密钥长度为gcd（4，24）=4的错误结论，所以这种方法有一定概率会产生差错。

本文主要讨论的简易算法对本小结的例子的处理将在2.1中进一步讨论。

2 简易算法

2.1 算法描述

卡西斯基试验法效率较高，但并不易行，本文中主要讨论以下算法：

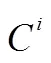
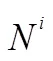
以1.3中的例子来说，如果将的前三位去掉后则得到：

明文：tomethatyoulovemeforevertomorrowmorning

密钥：skyskyskyskyskyskyskyskyskyskyskyskysky

密文：lykwdfsdwgejgfceodgbcnoplykgbpggkgblaxe

明文：saytomethatyoulovemeforevertomorrowmorn

密钥：skyskyskyskyskyskyskyskyskyskyskyskysky

密文：kkwlykwdfsdwgejgfceodgbcnoplykgbpggkgbl

而如果将的前两位去掉则可以得到：

明文：ytomethatyoulovemeforevertomorrowmorning

密钥：yskyskyskyskyskyskyskyskyskyskyskyskysky

密文：wlykwdfsdwgejgfceodgbcnoplykgbpggkgblaxe

明文：saytomethatyoulovemeforevertomorrowmorni

密钥：skyskyskyskyskyskyskyskyskyskyskyskyskys

密文：kkwlykwdfsdwgejgfceodgbcnoplykgbpggkgbla

2.2 算法分析

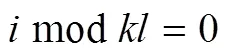
2.3 概率计算

假设对于明文序列中的每一位，26个字母均等概率出现，即每个字母出现的概率为1/26，则：

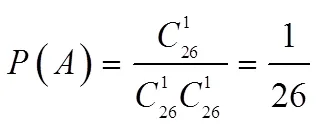
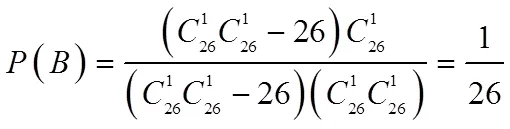
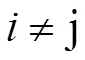
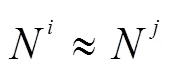
这一结果也将再下面的2.5中被实验证实。本节的假设将在3.2节中被引用。

2.4 字母频率

然而，在一篇有语义的英文文章中，26个字母并不是等概率出现在每一个明文位上的。

在英语中，各字母出现的概率如表1所示[5]。

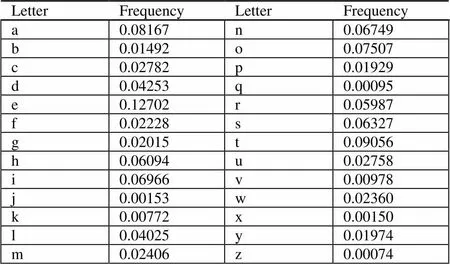
表1 英文字母频率

其中，出现频率最高的字母是e，其次是t。

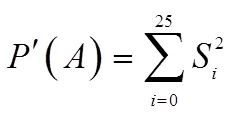
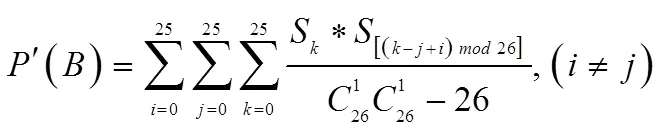
通过计算，可以得到

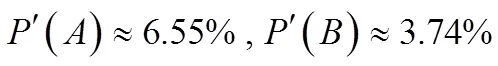
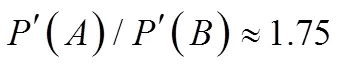
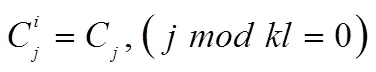
2.5 实验验证

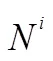
图1为其中一次计算的结果：

从条形图中也可以反映出来，我们无法有效的确定密钥长度。

对于等式（11），作者选择了一篇较长的英文文章，并剔除了标点符号，提取出了里面的2600个字母进行测试，同样选择随机的7位密钥，重复计算了100次数，结果为：

他们两者的比值为1.746

其中一次的结果如图2：

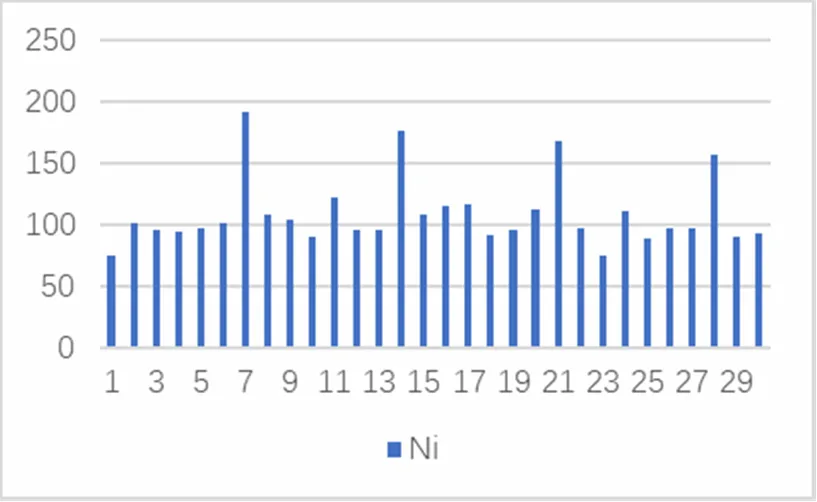
图2 明文有语义的维吉尼亚实验结果

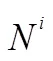
3 对流密码的破解

相较于维吉尼亚密码来说，该算法对于错误使用了OTP密码加密的破解效果更好。

3.1 错误的OTP加密

由于异或运算的对称性，流密码在加密和解密的时候使用同一个密钥。和维吉尼亚不同的是，流密码异或对于字母到数字的映射是使用的字符的ASCII，由于密钥流通常达不到明文的长度，所以往往是由一个较短的密钥通过一些伪随机生成算法来生成足够长的密钥序列，比如著名的RC4算法[7][8]。而如果拓展密钥的时候是像维吉尼亚密钥那样拓展的话，就会使得该密码算法很容易被破解。

“错误”即对密钥进行了错误的填充。对OTP密码的描述已在1.2节中阐述，倘若加密方拓展密钥长度时，只是将一个较短的密钥进行简单的复制填充以达到和明文长度一样的目的，那么便可以用本算法很轻易的得到密钥长度。即如果明文为say to me that you love me forever tomorrow morning，密钥为sky，则加密结果为：

明文：

say to me that you love me forever tomorrow morning

密钥：

skyskyskyskyskyskyskyskyskyskyskyskyskyskyskyskysky

密文：

0x000a00531f1653061c531f11121f590a040c530716050e591e0e5915040b161d1c014b0d1c0616011916044b141c19171a051e

可以发现，密文中会出现很多不可见的ASCII字符。

3.2 计算

异或流密码和维吉尼亚密码其中一处不同即在于异或流密码的明文空间和密钥空间应该是ascii可打印字符，而密文空间则可以是所有的ascii字符。

在查阅文献后作者仅找到了英文字母和空格在英文中的出现频率[6]如表2：

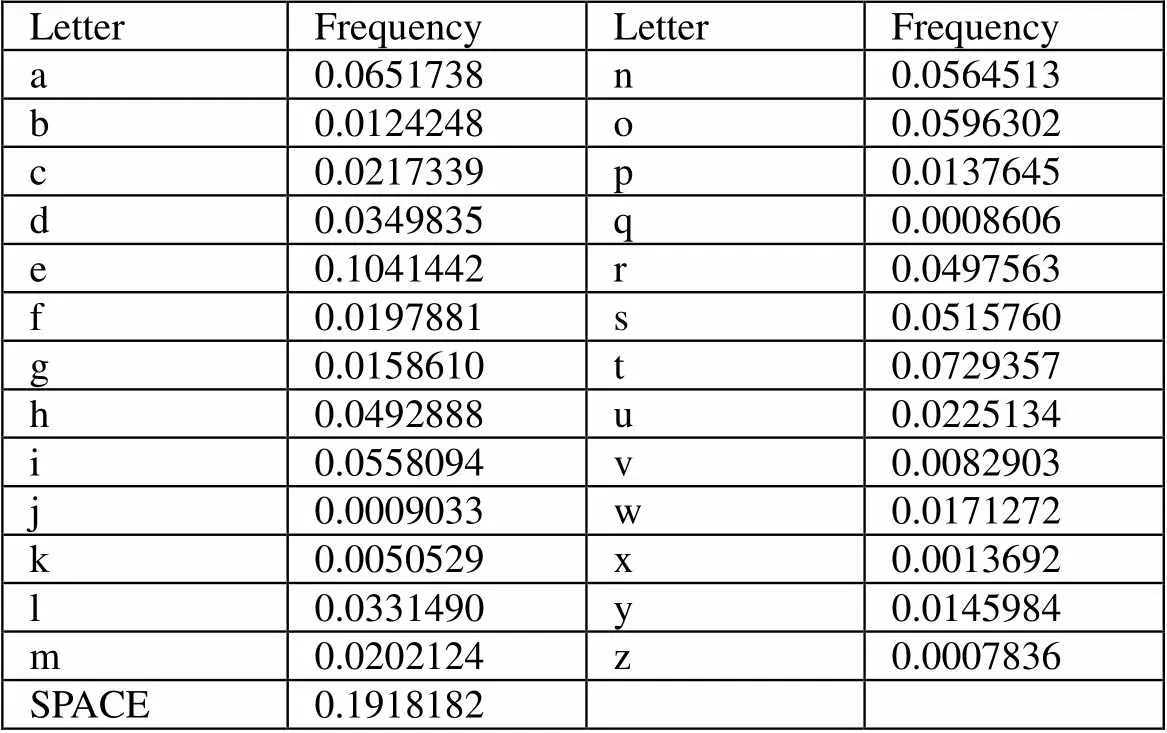
表2 英文中字母和空格的频率

则基于此数据展开讨论，引用2.2和2.3节的假设，再增设set为26个字母和空格的集合。

则若在明文和密钥中27个字符等概率出现：

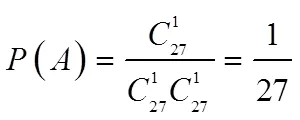
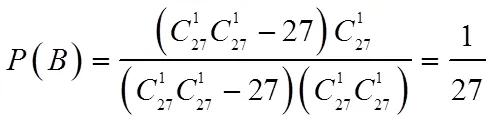
那么假设在明文中27个字母出现的概率为上图中的概率，进一步讨论有：

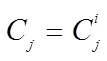
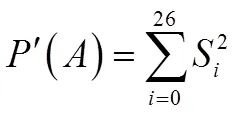
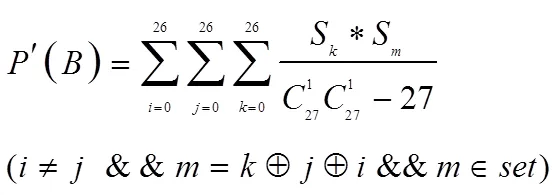
通过计算，可以得到：

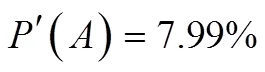
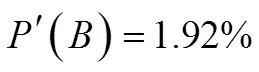
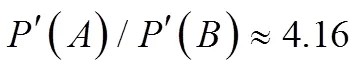
可以发现，等式（18）的比值是明显要比等式（11）的大的。

3.3 实例分析

对于等式（18），作者同样选择了一篇较长的英文文章，并剔除了标点符号，仅留下26个字母和空格作为明文进行测试，同样生成随机的7位密钥，重复计算了100次数，得到：

它们两者的比值为4.067

其中一次的结果如图3：

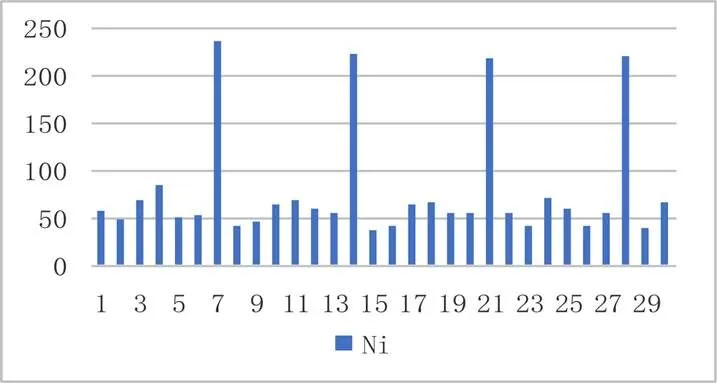
图3 明文有语义的异或加密实验结果

从图3中可以十分明显的看出密钥长度为7。

4 总结

尽管维吉尼亚密码在现代密码体系中已经用的不是很多了，但本算法对于重复使用了密钥的流密码来说，效果十分明显，可以从3.3中绘制的Ni条形图快速准确的得到密钥的长度。也从侧面反映出了香农提出的“完善保密性”的正确性，即密钥空间等于或者大于明文空间时，即使攻击者拥有无穷的计算时间和存储空间，密文仍不可能被破解。

[1]Klaus Pommerening. Kasiski's Test：Couldn't the Repetitions be by Accident?[J]. Cryptologia，2006，30（4）.

[2]Seongmin Park，Juneyeun Kim，Kookrae Cho，Dae Hyun Yum. Finding the key length of a Vigenère cipher：How to improve the twist algorithm[J]. Cryptologia，2020，44（3）.

[3]葛蓝.浅谈维吉尼亚加密算法的原理与实现[J].电脑与电信，2017（04）：64-65+86.

[4]Shannon C E. A Mathematical Theory of Communication[J]. The Bell System Technical Journal，1948，27.

[5]James Wiegold. CIPHER SYSTEMS：The Protection of Communications[J]. Bulletin of the London Mathematical Society，1983，15.

[6]Statistical Distributions of English Text [EB/OL].[2000-08-19].https://web.archive.org/web/20170918020907/http://www.data-compression.com/english.html.

[7]刘聪. 基于密钥流的RC4算法安全性分析与改进[D].湖南大学，2016.

[8]苑超，徐蜜雪，斯雪明.对不同种子密钥长度的RC4算法的明文恢复攻击[J].计算机应用，2018，38（02）：370-373.