带边界项的结构敏感性超像素图像分割方法研究
张建宇,张荣国,胡 静,刘小君,王 芳,李晓明
(1.太原科技大学计算机科学与技术学院,太原 030024;2.合肥工业大学机械工程学院,合肥 230009)
Ren等人[1]于2003年提出超像素是具有相似颜色、纹理、亮度等特征的空间上相邻的像素组成的像素块。将图像预处理为具有意义的超像素,可降低图像后续处理的复杂度,显著提高了计算效率。超像素分割作为图像处理的重要预处理步骤,已被广泛的应用于图像分割[2]、计算机视觉[3-4]等领域,如:显著性检测[5-6]、图像分割[7-8]、视频分割[9-10]等。
现存的超像素分割方法很多,其中结构敏感性超像素分割方法有SSS算法[11]和MSLIC算法[12],MSLIC算法继承了SLIC算法[13]的所有优点,如简单高效等,分割速度是SSS算法的十倍左右,并且在结构敏感性图像分割方面表现的非常好,但是基于欧式距离的RCVT[14]和正方形的搜索框,难以适应多样图像,所以在原有的基础上加入了边界特征,对单个像素在8领域检测超像素边界在真实图像边界的度量来进一步的优化提高分割的超像素质量,保证生成超像素更加贴合真实图像边界。实验证明加入边界项之后的算法生成的超像素在多个测量指标下的表现良好。
1 SLIC方法

2 MSLIC方法
MSLIC扩展了SLIC以计算结构敏感的超像素,同时它继承了SLIC的所有优点,例如简单性和高性能。MSLIC使用CIELAB颜色空间,将图像l中像素p=(u,v)的颜色表示为c(u,v)=(l(u,v),a(u,v),b(u,v)),定义了一个伸缩图Φ:l→5,将像素映射到包含颜色和空间5维向量的2维流形M[16]中,流型M中两点间的距离度量为:
(1)
通过平面三角形区域△Φ(p1)Φ(p2)Φ(p3)估算曲面三角形区域Φ(△p1p2p3):
Area(Φ(△p1p2p3))≈
(2)
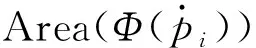
对于区域Ω⊂I⊂2,M上相应区域Φ(Ω)⊂M的面积取决于Ω的面积和Ω的强度或颜色变化。Ω中颜色的变化越大,Φ(Ω)的面积就越大,反之亦然。在M上计算统一的曲面细分,反映射Φ-1到图像l中就是结构敏感性超像素。
3 带边界项的结构敏感性超像素分割方法
MSLIC在2维流形M和输出结构敏感的超像素上生成统一的曲面细分。而根据Φ(Ω)的面积大小来衡量是否存在结构敏感性区域。能够高效快速的生成结构敏感性超像素,而基于颜色和欧氏距离的度量不能很好的保证超像素边界在真实图像的边界上[17],为进一步保证结构敏感性超像素的边界更加贴合真实图像边缘,故引入了新的测量,以p为中心的8连通领域上计算像素在真实图像边界上的可能性,其计算式为:
(3)
其中:R3(x)是以像素p为中心的8连通领域的所有像素的集合,并且pi∈R3(x),|R3(x)|是R3(x)中的像素总数,g(p)是像素p的梯度,γ是变化因子,Gδ是高斯系数。
如果像素p四周的像素pi的强度均匀的区域中,则g(pi)的值小并且与g(p)非常相似。如果像素p在图像边界上,则围绕它的像素的强度沿边界的正交方向变化极大,并且边界附近的像素的梯度值大,而其他像素的梯度值小。因此,w(p)变大。w(p)的值越大,对象边界上的像素p的概率越高。设计了一个边界项,使超像素的边缘与图像中的对象边界对齐:
(4)
其中:μ1和μ2是参数因子,δ2是ηkp的数学期望,ξ2是图像中w(p)的平均值。在以像素p为中心的局部窗口中,ηkp是其标签不等于k的像素数,该像素由该窗口中的像素总数归一化。ηkp计算为:
(5)
R3(x)′={p|p∈R3(x)},并且|R3(x)′|是集合R3(x)′中的元素的数量。在某种程度上,ηkp的值表示像素x是否在超像素的边缘上的概率。等式(5)由两个项组成,而第二个是每个像素的常数。因为无论像素是在图像中的物体边界上还是位于先前的超像素边缘上,它都可能在下一次迭代中属于超像素边缘。 这意味着只要B(p)和ηkp之间的一个值很大,ηkp的值就应该很大。因此,ηkp的公式应该是这两个部分的总和。边界项是为了确保超像素的边缘尽可能好地粘附到图像中的对象边界。该算法时间复杂度为O(N),其中N为像素个数。
4 实验结果对比分析
对算法进行评估的实验图片来自Berkeley标准数据集[18],为了验证改进算法的有效性,将其与现存的SLIC算法、LSC算法[19]、SEEDS算法[20]和MSLIC算法进行比较。接下来用召回率[21]、欠分割误差[21]和紧凑性[22]对算法分割效果进行了评估。实验表明改进后的分割方法表现良好。

表1 算法步骤及流程Tab.1 The algorithm steps and processes
实验环境:本算法实验在windows10,CPU 3.0 GHz,4 GB RAM的计算机上通过visual studio 2015来运行实现,通过使用matlab来进行实验评估。
①召回率:是测量边界贴合度的重要评估指标,广泛的应用于超像素分割来评估分割质量,召回率表示真实分割中边界的像素被检测到是否在超像素中。
②欠分割误差:测量与真实图像分割重叠的超像素的紧密度分割错误描述了真实图像分割重叠的超像素的紧密度。
③紧凑性:是紧凑性是规则边界的理想特性,对于给定区域边界长度,其面积形状越大,紧凑性越好。
因篇幅所限,本文仅展示两张分割效果图1和图2.两张原图是Berkeley数据集中481*321图像。

图1 人物图像分割Fig.1 Character image segmentation

图2 风景图像分割Fig.2 Scenery image segmentation
从上看出改进方法的分割表现非常的好,但为了进一步评估算法性能的真实情况,我们使用以上六种评估指标,选取Berkeley数据集中编号为6046的动物图像在不改变原始参数的情况下,将LSC算法、SEEDS算法、SLIC算法、MSLIC算法和改进算法,每个算法迭代五次生成实验数据来进行试验评估。
其中图3为召回率对比曲线图,图4欠分割误差对比曲线图,可以从对比曲线图中看出,改进的方法有着明显的优势,改进的方法的各方面表现明显好于原MSLIC方法,边界贴合度得到了明显的提升,证明了改进算法的可行性,加入边界项度量对生成超像素的表现有着明显的影响。

图3 召回率对比曲线图Fig.3 The comparison of recall

图4 欠分割误差对比曲线图Fig.4 The comparison of under-segmentation errors
图5为紧凑性分割对比图,从对比曲线图可以看出改进的算法紧凑性方面所下降,这是因为加入边界项度量所导致的,然而对原MSLIC算法进行改进便是为了提高算法的边界贴合度,以便提高后续图像处理的准确度,紧凑性的下降同样在预期之中。
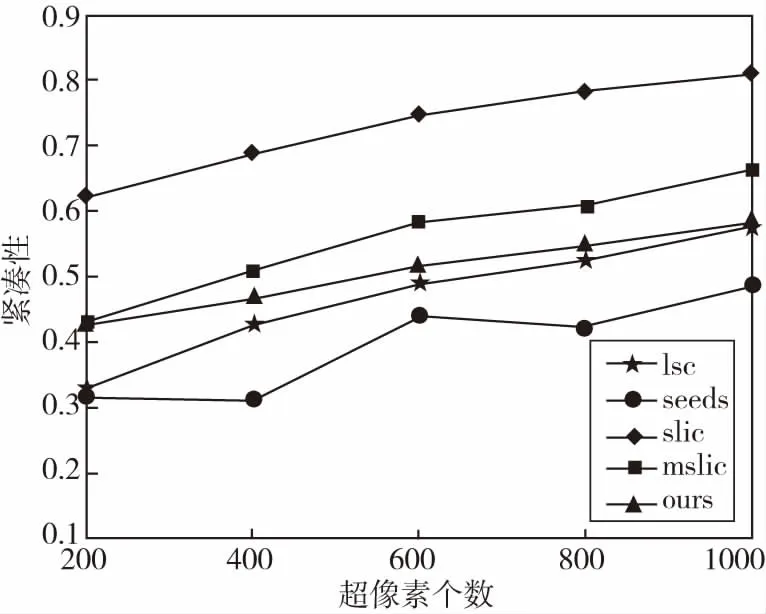
图5 紧凑性对比曲线图Fig.5 The comparison of compactness
表2给出Berkeley数据集编号为3063、368037、5096数据的评估结果,将LSC、SEEDS、SLIC、MSLIC和改进算法均预分割200个超像素。给出了欠分割误差,召回率、紧凑性的具体评估结果。

表2 三种算法在评估指标下的评估结果Tab.2 Evaluation results of five algorithms under evaluation indicators
5 结论
结构敏感性超像素可以生成大小不一的超像素,更加能够保证生成超像素内部信息一致。在原有的MSLIC算法的基础上加入边界项来判别像素是否在真实图像边界上的,从而进一步优化生成超像素。实验对比了LSC算法、SEEDS算法、SLIC算法、MSLIC算法。结构表明改进方法在边界贴合度和可实现分割准确度上更具有优势,更加有利于后续图像处理。虽然算法在运行速度上要低于原算法,但在保证其他性能提高的情况下可以接受。

