荷载作用下桥梁振动控制研究

刘 莉

(辽宁省交通运输事业发展中心 沈阳市 110005)

地震、风、车辆等随机荷载作用于桥梁上时都将引起桥梁振动，而随着车辆数量增多、载重量增大、速度增高等会更加剧桥梁的振动。这对桥梁结构的正常使用及安全是不利的，因此需要在设计上进行振动控制。而车辆振动和其它动力荷载己经成为桥梁设计、施工、管理、养护、维修等方面的重要因素之一。为了进一步探究荷载作用下振动对于桥梁的影响，对运营20年旧桥的16m先张预应力混凝土空心板原桥梁板进行减振试验。

1 减振试验方案

车辆行驶过桥梁的过程分为两个阶段，阶段一是车辆在上桥开始后直至下桥阶段，结构在车桥耦合振动作用下进行随机振动，如图1、图2为重车行

驶在某桥上跨中的加速度监测结果，从监测曲线可以看出结构响应并无明显规律性。

阶段二为车辆下桥后，结构荷载突然消失，结构由于惯性力的存在将进行自由振动，自由振动响应幅度与结构自身阻尼大小有关。如图3、图4为重车通过某桥跨中的加速度监测结果。

因此，本次的减振试验将模拟两个阶段进行，分别为结构自由振动试验和结构随机振动试验，同时为了获取结构的幅频特性、阻尼器安装位置影响、减振效果等，还需进行结构的正弦振动试验。本次试验过程中主要的量测仪表如表1。

表1 试验仪器设备一览表

试验采用辽宁省已经运营20年真实旧桥的16m先张预应力混凝土空心板原桥梁板，截面尺寸及配筋如图5。

2 试验梁动力特性有限元计算及TMD 阻尼器设计

在进行TMD阻尼器参数设计前要获得结构的自振特性，即结构的自振频率。梁板全长15.96m，带铺装结构总重为20.3t。利用有限元程序midascivil和sap2000建立桥有限元模型，结构阻尼比取0.005。为了验证模型的准确性，采用特征向量法计算出了结构前3阶动力特性，并将前3阶计算结果进行对比，sap2000 模型与midas 模型的频率十分吻合，可用于动力分析。

表2 有限元计算结构频率

本次试验TMD的设计参数如表3所示。

表3 TMD 阻尼器参数设计

由于空心板的一阶频率为6.15Hz，非常接近6Hz，会发生共振响应，由图6可知，6.0Hz 时结构发生了共振，其稳态加速度为19.28m/s2，有控时，结构的稳态加速度为 1.50m/s2，TMD的减振率达到了92%。

3 结构正弦振动试验研究

正弦振动在任意一瞬间只包含一种频率的振动，一般来说，结构正弦振动的试验目的在于找出结构的脆弱点，看在哪一个具体的频率点结构的动力响应最大，即所谓的结构共振点(Resonant Frequency)。见图6。

3.1 试验目的

(1)测试结构的共振点并确定结构需要减振的频率范围。

(2)测试结构固有的频率响应关系。

(3)测试结构振动沿跨径方向的影响。

(4)测试阻尼器对指定频率的减振效果及有效减振范围。

试验方法：

为了模拟 0～4m/s2的振动，对16m预应力混凝土空心板梁，连续施加给试件的一组3kN振幅的单频正弦振动过程。手动调整激振频率1～7Hz的范围内，由MTS动态加载系统补偿功能来保持力的幅值，设置的试验条件包括单组的固定频率、试验持续时间、位移和加速度的幅值。

3.2 试验内容

(1)无阻尼器正弦振动1～7Hz。

(2)1个阻尼器(质量比 0.5%)正弦振动 1～7Hz。

(3)3个阻尼器(质量比 1.5%)正弦振动 1～7Hz。

(4)5个阻尼器(质量比 2.5%)正弦振动 1～7Hz。

3.3 试验结果对比分析

试验梁频率与跨中加速度响应的关系如图7所示。

(1)从图7的频响关系可以看出，当结构未安装阻尼器时，在 6.34Hz 处产生最大的振动响应，即结构发生共振的频率，以共振频率为中心频率附近对称的频率响应同样很大。

(2)当结构安装1个阻尼器后，结构的频响关系曲线发生了变化，由原单峰形变为了双峰形，在 6.44Hz 处频响曲线出现谷地；从频响的幅值可以看出，加速度明显变小，结构减振效果明显，当安装一个阻尼器时减振率为45%；当结构安装3个阻尼器后，结构减振控制效果更为明显，减振率为72%；当结构安装5个阻尼器后，减振曲线趋于平缓，结构减振控制效果更为明显，减振率为81%。

(3)图8为结构振动沿跨径方向的影响经归一化处理后的结果，从图中可以看出各次试验结果基本重合，阻尼器与结构协同工作的性能良好，结构四分点截面处的振动响应约为跨中响应的 0.757倍。

4 结构自由振动试验研究

车辆通过桥梁后结构会产生自由衰减振动，为了了解阻尼器对车辆通过桥梁后结构的减振效果，需对其进行试验研究。实验室内模拟结构自由振动通常是借助于外荷载使结构产生一初位移(或初速度)，使结构由于弹性而自由振动起来，由此记录振动波形，从而获得结构自振特性并了解结构自由振动水平。

4.1 试验目的

(1)研究汽车通过桥梁后结构的振动响应。

(2)研究结构自由振动沿跨径方向的影响。

(3)测试阻尼器对结构自由振动的减振效果及有效减振范围。

(4)研究TMD阻尼器数量(质量比)对结构阻尼比的影响。

试验方法：

在16m 预应力混凝土空心板梁上预先施加一个 50kN 的静力荷载，利用 MTS 动态加载系统的快速复位功能突然释放静力荷载，有阻尼结构由于惯性力的作用将进行自由衰减振动。

4.2 试验内容

(1)无阻尼器自由振动。

(2)1个阻尼器(质量比 0.5%)自由振动。

(3)3个阻尼器(质量比 1.5%)自由振动。

(4)5个阻尼器(质量比 2.5%)自由振动。

4.3 试验结果对比分析

结构自由振动跨中加速度衰减曲线对比如图9所示。

从试验的对比曲线可以看出，前三个振动周期(约为0.5s)内阻尼器对结构振动没有起到作用，可以看出作为被动减振的TMD阻尼减振系统对结构减振存在延迟时间，无法对自由振动起振时的最大幅值进行控制。

当阻尼器受到惯性力而发挥作用后，3个和5个阻尼器对结构振动的抑制作用是明显的，从能量衰减的角度可以看出 TMD 阻尼器对自由衰减振动全过程的振动控制能力也是明显的。从衰减曲线的阻尼比分析结果可知，1 个阻尼器对原梁的阻尼增加并不明显。3 个阻尼器时阻尼比增加了62%，5 个阻尼器时阻尼比增加了 90%。

5 结构随机振动试验研究

随机振动指那些无法用确定性函数来描述，但又有一定统计规律的振动。例如车辆行进中的颠簸，阵风作用下结构的响应，喷气噪声引起的舱壁颤动以及海上钻井平台发生的振动等等。振动可分为定则(确定性)振动和随机振动两大类。它们的本质差别在于：随机振动一般指的不是单个现象，而是大量现象的集合。这些现象似乎是杂乱的，但从总体上看仍有一定的统计规律。因此随机振动虽然不能用确定性函数描述，却能用统计特性来描述。在定则振动问题中可以考察系统的输出和输入之间的确定关系；而在随机振动问题中就只能确定输出和输入之间的统计特性关系。本次试验是对试验梁施加一时间历程的激励来模拟汽车在桥梁上的行车作用。

5.1 试验目的

(1)通过短持续时间的随机力作用模拟汽车在桥梁上的行车作用。

(2)测试结构随机振动沿跨径方向的影响。

(3)研究TMD阻尼器数量(质量比)对结构随机振动减振效果的影响。

(4)测试阻尼器对指定频率的减振效果及有效减振范围。

试验方法：

在16m预应力混凝土空心板梁上，利用MTS 动态加载系统的Random随机函数发生器功能，通过设置随机波的波形形式、频带范围、幅值力的范围模拟行车在桥上随机振动的行为。频带范围为结构一阶自然频率6.4Hz的±20%，即5.12～7.68Hz。随机振动波形采用5个随机函数，1/F2、1/F、Flat(未放大信号高频部分)、F、F2。

5.2 试验内容

(1)无阻尼器随机振动。

(2)1个阻尼器(质量比0.5%)随机振动。

(3)3个阻尼器(质量比1.5%)随机振动。

(4)5个阻尼器(质量比2.5%)随机振动。

5.3 试验结果对比分析

从表4中可以知，Random-1/F2随机振动的方式下结构跨中减振率为 0～5%,减振效果十分有限。

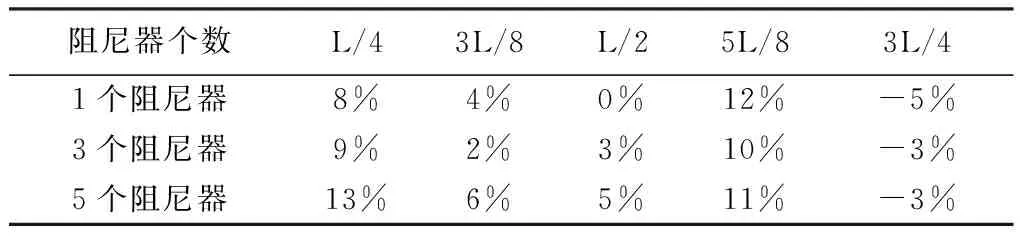
表4 Random-1/F2随机振动减振率

从表5中可以知， Random-1/F 随机振动的方式下结构跨中减振率在14%～16%。

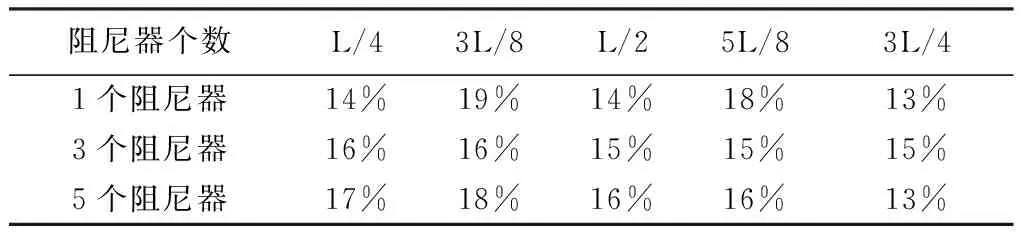
表5 Random-1/F 随机振动减振率

从表6中可以知，Random-Flat 随机振动的方式下结构跨中减振率在 2%～14%。

表6 Random-Flat 随机振动减振率

从表7中可以知，Random-F 随机振动的方式下结构跨中减振率在 11%～19%。

表7 Random-F 随机振动减振率

从表8中可以知，Random-F2随机振动的方式下结构跨中减振率在 11%～14%。

表8 Random-F2 随机振动减振效果

6 总结

通过结构正弦振动试验、自由衰减振动试验、随机振动试验模拟验证了调谐质量阻尼器的减振效果，并进行了MTMD参数优化及验证，最终得出了以下结论：

6.1 正弦振动试验

(1)当结构安装 TMD 阻尼器后频响曲线明显幅值变小,并且将从原单峰曲线变为多峰曲线，曲线峰峰间的谷点出现在阻尼器调节频率附近，该现象表明调谐质量阻尼器对调节频率处的振动有较好的控制效果。

(2)在共振频率±0.3Hz 范围内结构的频响均为共振频响的 70%以上，因此除了需要对共振频率进行控制，对共振频率附近的频率同样需要进行控制。

(3)阻尼器的个数(即质量比)对结构振动的减振影响并不是呈线性增大变化，而是存在较为理想的质量比范围，质量比过小减振效果不明显，质量比过大将对结构产生负影响，一般质量比应控制在 0.5%～3.0%，在此质量比范围内质量比越大减振效果越明显。

(4)参数相同的分布式阻尼器的数量和位置并不影响梁板沿跨径方向的振动特性，对于简支结构而言，阻尼器与结构均能体现较好的协同工作性能，阻尼装置安装于桥面同样可以实现结构减振的目的。

6.2 自由振动试验

(1)作为被动减振的TMD阻尼减振系统对结构减振存在延迟时间，无法对自由振动起振时前几个周期的最大幅值进行控制。

(2)当阻尼器受到惯性力而发挥作用后，从能量衰减的角度可以看TMD阻尼器对自由衰减振动全过程减振效果明显。

(3)当阻尼器质量比较小时，对结构的阻尼增加并不明显，从而控制自由衰减振动能力较弱。

6.3 随机振动

通过5种随机振动方式模拟试验结果可知，当结构振动频率变化较快时，阻尼器对结构的减振能力十分有限，最大减振率约为0～19%，因此对于车桥振动而言阻尼器对车辆行驶于桥上的振动减振效果并不明显。

由以上的试验结果可知，辽宁省公路桥梁处于重型交通范围内较多的桥梁为16～20m跨径的桥梁，重型交通桥梁的一阶频率与峰值点振动频率差值范围为-3%～15%，应对其共振频率进行减振控制。