小波和混沌神经网络在大坝变形预测中的应用

康传利　陈洋　张临炜　时满星　顾峻峰

摘 要：大坝是复杂的变形系统，其变形表现为动态非线性，也存在混沌现象。为充分利用大坝变形监测位移时间序列，实现位移单变量情况下的准确预测，提出了一种小波和混沌神经网络预测新方法，首先对大坝位移变形监测数据进行小波分解，其次对分解后的平滑信号进行傅里叶函数拟合预测，再对细节信号进行软阈值去噪和混沌神经网络预测，最后将预测信号进行小波重构。通过工程实例对比分析了小波和混沌神经网络预测新方法、神经网络模型、多元回归模型在大坝位移变形预测中的精度。结果表明，小波和混沌神经网络预测方法的预测精度最高，可以应用于大坝变形预测。

关键词：相空间重构; Lyapunov 指数; 小波分解和重构; 小波去噪; 混沌神经网络预测; 大坝变形

中图分类号：TV698.1   文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.03.020

Application of the Wavelet and Chaos Neural Network for Monitoring Dam Deformation

KANG Chuanli1，2， CHEN Yang1，2， ZHANG Linwei1，2， SHI Manxing1，2， GU Junfeng1，2

（1.Guangxi Key Laboratory of Spatial Information and Geomatics， Guilin 541006， China;

2.College of Geomatics and Geoinformation， Guilin University of Technology， Guilin 541006， China）

Abstract： Dam is a complex system， which deformation manifested as dynamic nonlinear and may appear chaotic phenomenon in sometimes. In order to make full use of monitoring data and realize the accurate prediction in case of one variable， this paper put forward a new method of forecasting， which used wavelet to decompose monitoring data， Fourier function to fit smooth signal， soft threshold in wavelet to denoising， chaotic neural network to predict detail signal and wavelet to reconstruct forecast signal. The prediction accuracy of the new method， neural network model and multiple regression model in dam displacement deformation were analyzed by engineering examples. It is found that the prediction method of wavelet and chaos neural network is reliable and has high precision. Therefore， this model can be used in dam deformation prediction.

Key words： phase space reconstruction; Lyapunov index; wavelet decomposition and reconstruction; wavelet denoising; chaotic neural network prediction; dam deformation

大壩是复杂的变形系统[1]，大坝变形不仅受到温度、水压以及时效等的影响，还受到大坝内部各要素之间内在随机性的影响，因此大坝在不同条件和环境下表现出复杂的非线性行为。高精度的大坝变形预测为快速判断大坝安全状态、准确识别险情、保障大坝安全运营提供理论基础。大坝系统的复杂性和多样性使得常用预测方法在大坝变形预测中精度较低：GM（1，1）预测只适应于解决呈指数变化的数据，卡尔曼滤波预测容易受到先验信息的影响，而神经网络预测容易陷入局部最小点。近年来不少学者尝试对预测方法进行优化，取得了一系列成果[2-6]，虽然在一定程度上优化了预测方法，但是这些改进方法都没有考虑大坝内部各要素之间的随机性，在位移单变量条件下难以实现精准预测。大坝变形表现出非连续性变形，含有突变和混沌现象。传统的时间序列都是基于一维空间，而一维的时间序列结构单一，所包含的信息量较少，致使预测精度受到限制。根据Takens定理[7]，将时间序列转化到一个合适嵌入维数的空间能够恢复系统原有规律。因此，对大坝位移时间序列进行相空间重构有望使预测精度得到提高。

在大坝变形观测中，受测量仪器、外界条件和观测者的影响，观测数据不可避免地包含误差，小波理论因其良好的去噪效果而在测量中得到广泛应用[7]。鉴于常用预测模型的特点和适用范围，笔者提出了一种预测新方法，该方法运用小波理论对观测数据进行分解，并对细节信号进行去噪，再用混沌神经网络对细节信号进行预测，最后将预测数据进行小波重构。通过工程实例，将新方法同RBF神经网络、多元线性回归预测精度进行对比，证实新方法在大坝变形预测中的可行性和优越性。

1 混沌神经网络分析

1.1 C-C法相空間重构

混沌系统的时间序列包含着丰富的动力学信息，相空间重构法是将一维时间序列扩展到三维或更高维数的空间，其目的是充分挖掘隐含在一维时间序列中的相关分量信息。相空间重构法能够对时间序列本身存在的混沌吸引子进行恢复并对其演化规律进行研究，需要确定最佳嵌入维数m和延迟时间τ，笔者采用C-C法计算m和τ[7]。

1.2 Wolf算法求解最大Lyapunov 指数

混沌系统的一个重要特征就是对初始条件敏感依赖，混沌系统对初始条件的敏感性使得长时间预测不可能实现。离散程度可以用最大Lyapunov指数来度量，最大Lyapunov指数常用Wolf算法计算，主要计算步骤如下[8-9]。

设混沌时间序列{x1，x2，…，xn}，则相空间重构后的序列为

Y（ti）={x（ti），x（ti+τ），…，x[ti+（m-1）τ]}（1）

式中：i=1，2，…，N。

取初始点Y（t0），设其与最近邻点Y0（t0）的距离为L0。随着时间的推移，直到t1时刻这两点的距离超过规定值ε，即L′0=|Y（t1）-Y0（t0）|>ε，则保留Y（t1），并在Y（t1）附近寻找夹角尽可能小的另一个距离小于ε的点Y1（t1），即L1=|Y（t1）-Y1（t1）|<ε，重复上述过程直到时间序列的终点N处。设总的迭代次数为M，则最大Lyapunov指数为

λ=1tM-t0∑Mi=0lnL′iLi（2）

1.3 混沌神经网络分析

神经网络具有较强的自组织能力、学习能力、自适应能力以及强大的非线性映射能力，因此神经网络广泛应用于工程预测、灾害控制、模式识别等[10]。神经网络的输入节点个数应根据需要确定，输入节点过多将会增加学习时间和降低模型精度，输入过少将不能很好地反映系统的客观规律。利用重构相空间中饱和嵌入维数作为神经网络的输入节点，能够避免节点选取的任意性和防止大坝变形信息的丢失，因此笔者对重构后的相空间时间序列使用神经网络进行预测，并用最大Lyapunov 指数确定预测期数的预测方法，有望提高预测精度。

2 小波和混沌神经网络预测

大坝的变形监测数据通常包含众多随机噪声，小波分析以其良好的时频局部化和多分辨率分析的能力而在测量数据处理领域得到广泛的应用。对大坝变形数据进行小波多尺度分解能够提取大坝空间变形趋势和进行奇异性探测，运用重构技术，可以有效滤除观测信号的噪声[10]，进而提高变形数据预测精度。

对原始数据进行小波多尺度分解将产生平滑信号和细节信号[11]，平滑信号反映大坝变形趋势应予以保留，而细节信号包含噪声和部分有用信息。因为平滑信号变化较为平缓且任意曲线都可用一组正余弦函数表示，所以笔者选用傅里叶函数对平滑信号进行拟合逼近，在得到数学表达式后，再对平滑信号进行预测。

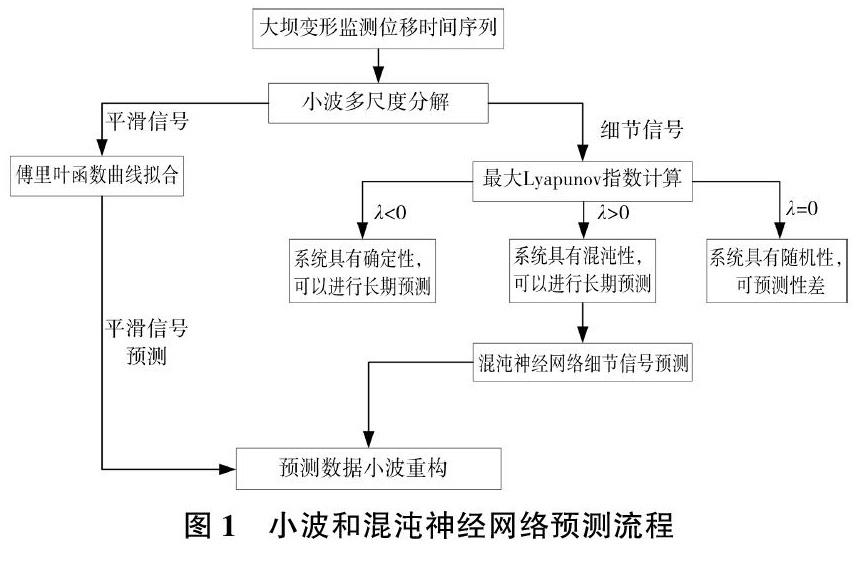
小波分析中的阈值去噪法可以很好地区分细节信号中的噪声和有用信号，混沌理论中的相空间重构能够直观方便地显示系统的结构和特性。鉴于此，笔者提出一种大坝变形预测的新方法，首先利用小波阈值法对细节信号去噪，然后对去噪后的细节信号进行混沌特性判断，通过混沌神经网络预测方法对各层细节信号进行预测，再将平滑信号预测曲线和去噪细节信号预测曲线进行小波重构。小波和混沌神经网络预测流程见图1。

3 大坝变形监测位移预测分析

大坝变形监测是确保大坝正常运行的基础，为验证本文提出的新方法在大坝位移预测中的可靠性和可行性，现以某混凝土拱坝坝顶监测点A1在2006年361 d的径向位移和切向位移为试验数据，其监测周期为1 d。本文使用A1点前330期位移数据进行建模，后31期进行预测验证，其位移变化见图2。由图2可知，A1点径向位移变化比较平缓，具有一定的规律性，而切向位移变化幅值小，但是波动大，变化不稳定，随机性强，呈现非线性变化趋势。显然，从图2中无法辨识大坝变形真实的变化趋势和突变点，对后期位移进行精准预测，就要采用更加精细的算法来深入挖掘大坝变形内在信息。

3.1 小波函数选取和平滑信号逼近

小波多尺度分解能将位移信号在不同尺度上进行分解。本文选用具有代表性的Haar、db6、db10和sym6小波函数对大坝位移原始离散数据进行3层小波分解[8]，计算每一个函数的最小均方根误差。根据最小均方根误差确定分解函数：径向位移选用db6小波函数，切向位移选用db10小波函数。

原始信号经过小波分解后被分解成1个平滑信号和3个细节信号。当对平滑信号采用傅里叶函数进行曲线拟合时，径向位移拟合函数的均方根误差RMSE=0.227 1 mm，切向位移RMSE=0.048 8 mm，拟合函数RMSE都较小，拟合效果见图3。由图3可知，原始值围绕拟合值上下波动，且波动幅度较小，因此采用傅里叶函数处理平滑信号拟合效果较好。

3.2 细节信号噪声去除

细节信号既包含有用信号也包含噪声，选用db6小波函数对细节信号进行3层小波阈值去噪处理，其中第1层细节信号RMSE=0.022 29 mm、第2层细节信号RMSE=0.020 21 mm、第3层细节信号RMSE=0.001 00 mm，去噪效果见图4。由图4可知，随着细节信号层数的增加，信号变得更光滑，信噪比增大。

3.3 小波和混沌神经网络预测

对细节信号进行小波去噪处理后，需对去噪细节信号进行混沌状态判断。去噪细节信号最大Lyapunov指数和细节信号RMSE见表1。由表1可知，细节信号RMSE随着层数的增加而减小，最大Lyapunov指数都大于0，这说明每层细节信号均存在混沌现象。

运用混沌神经网络对每层去噪细节信号进行预测，首先使用C-C法计算每层去噪细节信号的最佳嵌入维数m和延迟时间τ（见表2），然后依据m和τ进行相空间重构，依据重构后的时间序列使用BP神经网络预测。当平滑信号和细节信号预测完毕后就可以利用小波函数对细节信号和平滑信号进行小波重构，径向位移和切向位移实测数据及其预测值见图5。由图5可知，预测值同原始值残差较小，预测效果较好。

3.4 各模型预测对比分析

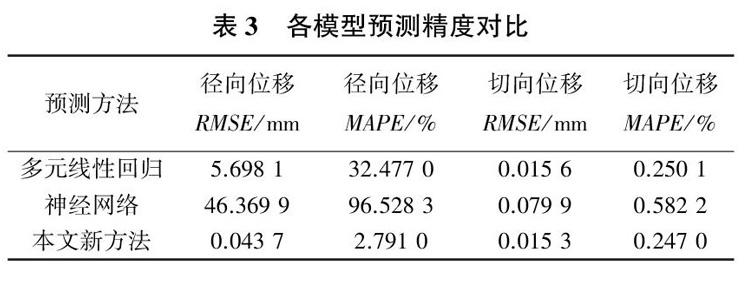
为了验证小波和混沌神经网络在大坝变形预测中的可行性，选用多元线性回归、RBF神经网络算法同小波和混沌神经网络新方法预测结果进行对比分析，其中多元线性回归的回归系数为7（依据最小RMSE），RBF神经网络算法中节点最大数目为7（依据表2中最大嵌入维数），其余参数均为默认值，其预测位移和残差见图6、图7。从图6、图7可以看出，由于大坝变形呈非线性、不稳定性和随机性变化，因此多元线性回归前期预测效果较好，但随着期数的增加，精度降低，这说明多元线性回归不适合长期预测;神经网络预测方法虽然具有强大的非线性映射能力，但当输入节点数不是最佳并且没有进行相空间重构时，预测精度下降，预测数值准确性差。表3列出了各预测模型的预测均方根误差和平均绝对百分比误差（MAPE）[4]，由表3可知，本文新方法的RMSE和MAPE均最小。由表3和图6、图7分析可知，本文新方法使用了小波理论对大坝变形数据进行小波去噪和小波分解，使用相空间重构挖掘一维时间序列空间规律，并利用神经网络对相空间时间序列进行非线性预测，考虑因素全面，进而提高了预测精度。

4 结 论

（1）大坝变形中有一些影响因子随时间变化，其变形呈弱混沌状态。将混沌理论应用于大坝位移预测，客观地反映了大坝变形的真实形态。

（2）小波多尺度分解能够提取大坝空间变形趋势和进行奇异性探测。运用小波软阈值去噪技术，可以有效滤除监测值中的噪声。

（3）小波和混沌神经网络算法同时拥有混沌理论能充分利用一维时间序列的优势和神经网络强大的非线性映射能力。小波和混沌神经网络预测方法能够保留细节起伏信息， 可以对呈现非线性变化的大坝位移进行预测，且预测精度高。

参考文献：

[1] 张正禄，黄全义，文鸿雁，等.工程的变形监测分析与预报[M].北京：测绘出版社，2007：6-18.

[2] 胡纪元，文鸿雁，周吕，等.遗传小波神经网络在大坝变形预测中的应用[J].人民黄河，2014，36（10）：126-128.

[3] 焦明连，蒋廷臣.基于小波分析的灰色预测模型在大坝安全监测中的应用[J].大地测量与地球动力学，2009， 29（2）：115-117.

[4] 任超，梁月吉，庞光峰，等.最优非负变权组合模型在大坝变形中的应用[J].大地测量与地球动力学，2014，34（6）：162-166.

[5] 任超，梁月吉，庞光锋，等.基于灰色最小二乘支持向量机的大坝变形预测[J].大地测量与地球动力学，2015，35（4）：608-612.

[6] 胡纪元.神经网络优化模型在大坝变形预报中的应用研究[D].桂林：桂林理工大学，2015：6-16.

[7] 修妍.混沌时序分析中的若干问题及其应用研究[D].天津：天津大学，2007：16-40.

[8] 吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉：武汉大学出版社，2005：57-85.

[9] 金玉婷.基于混沌和小波神经网络的短时交通流预测方法研究[D].成都：西南交通大学，2014：12-21.

[10] 陶珂，朱建军.小波去噪质量评价方法的对比研究[J].大地测量与地球动力学，2012，32（2）：128-133.

[11] 栾元重，栾亨宣，马德鹏，等.桥梁变形数据小波去噪与混沌预测[J].大地测量与地球动力学， 2013，33（5）：133-135，139.

【责任编辑 马广州】

收稿日期：2017-07-25

基金項目：国家自然科学基金资助项目（41461089， 41541032）;广西空间信息与测绘重点实验室基金项目（桂科能1638025-26，163802515，151400720）;广西高校科学技术研究项目（KY2015YB126）;广西研究生教育创新计划项目（YCSW2017155）

作者简介：康传利（1979—），男，山东郓城人，讲师，博士，研究方向为“3S”集成技术理论与应用

通信作者：陈洋（1991—），男，湖南益阳人，硕士研究生，研究方向为变形监测与数据处理

E-mail：hntj_cy@163.com