黄河下游右岸堤防典型段溃决过程研究
梁艳洁 罗秋实 赵正伟

摘 要:结合历史溃口、河防工程、河势影响和社会经济生态影响等情况,选择高村和胡家岸作为黄河下游堤防右岸典型段溃口位置,建立平面二维溃堤模型,对溃口溃决过程进行模拟,分别采用高村和艾山水文站1982年型近1 000 a一遇洪水过程作为进口流量,对典型河段溃堤过程中洪水演进、溃口冲深和展宽、横断面发展等进行分析,重点研究了溃口口门发展过程及分洪流量过程。计算结果表明:高村、胡家岸溃口最终宽度分别为900、720 m,分流比分布分别经过2、3 d之后达到稳定,为80%和75%。
关键词:溃堤模型;溃口流量;分流比;黄河下游
中图分类号:TV871.3;TV882.1 文献标志码:A
doi:10.3969/j.issn.1000-1379.2020.03.004
Study on the Typical Right Embankment Erosion Process of the Lower Yellow River
LIANG Yanjie, LUO Qiushi, ZHAO Zhengwei
(Yellow River Engineering Consulting Co., Ltd., Zhengzhou 450003, China)
Abstract:Based on the situation of historical breach, river control project, river regime situation and socio-economic ecological impact, Gaocun and Hujia section banks were selected as the locations of typical dyke breaches in the lower Yellow River. A 2-D mathematical model was established to simulate the breach extension process, the thousand year frequency flood of 1982 in Gaocun and Aishan hydrology stations were respectively adopted as the inlet discharge, the flood evolution, the depth and width of the breach and the cross section development in the course of dyke breaking were analyzed. The development process of the breach and the flood diversion discharge were studied. The calculated results show that the final width of Gaocun and Hujia bank breach is 900 m and 720 m respectively. The breach diversion ratio is 80% and 75% respectively after 2 and 3 days. The research results provide technical support for the analysis of breach discharge of flood risk map in the flood protection area of the Lower Yellow River.
Key words: dike-breach model; breach discharge; diversion ratio; Lower Yellow River
1 概 述
黄河下游河道是典型的地上悬河,部分河段还具有“二级悬河”的显著特征,历史上曾多次发生溃堤。人民治黄以来,黄河下游防洪一直是治黄的首要任务,随着社会经济发展和城市化进程的加快,黄河下游防洪安全更加重要,堤防安全问题成为重点研究对象。
根据《全国重点地区洪水风险图编制项目实施方案(2013—2015年)》,黄河水利委员会组织编制完成了《黄河流域洪水风险图编制项目实施方案(2014年)》,开展黄河下游堤防潰口专题研究是黄河流域洪水风险图编制项目的重要组成部分,也是开展防洪保护区洪水分析的重要前提。
据统计,1855—1935年兰考—东明—东平湖河段发生堤防决口年份有34 a,决口53处,其中兰考(东坝头)—东明河段决口19处、东明至东平湖(桩号336+600)决口24处。按照决口性质统计,堤防冲决占44%,漫决占20%,溃决占19%,其他占17%,可见冲决是该河段堤防决口的主要形式。济南以下河段发生堤防决口年份有24 a,决口54处。按照决口性质统计,堤防冲决占24%,漫决占17%,溃决占39%,其他占20%。可见历史上黄河下游堤防溃决应该以冲决和溃决为主,漫决所占比例较小[1]。人民治黄以来,随着黄河下游防洪工程体系的建设,黄河下游堤防工程防护标准已经提高到近1 000 a一遇,大洪水漫决的机遇非常小,因此未来黄河下游堤防最可能的决口形式为溃决和冲决[2-3]。
结合历史溃口、河防工程、河势影响和社会经济生态影响等情况,选择高村和胡家岸作为风险最不利的、能够包括全部风险的河段和溃口布设位置,采用平面二维溃堤模型对溃口溃决过程进行模拟,研究口门发展过程、口门形式及分洪过程,为黄河下游防洪保护区的洪水风险图编制提供技术支撑。
2 溃口位置布设及设计洪水过程
2.1 黄河下游溃口位置布设
影响堤防溃口过程和分流比的因素可归纳为3方面:一是溃口处的堤防条件,如堤防土质结构、土力学特性等[4];二是溃口处的水动力因子,如溃口内外水位差、溃决流量、持续时间等;三是溃口处大河河势,如主流与堤防夹角。
高村溃口(桩号204+000附近)位于黄河下游兰考至东平湖河段中间(见图1),处于黄河由宽河至窄河的过渡河段。该河段堤防土质松散,右岸堤防多年靠河,目前溃口断面附近主槽距离右岸大堤99 m,曾于1878年、1880年、1921年多次决口。该河段悬河形势严峻,滩面与堤外高差达4.56 m,堤防溃决之后淹没范围广大,损失严重。为此,黄河下游兰考至东明、东明至东平湖河段右岸防洪保护区选择高村溃口为典型溃口。
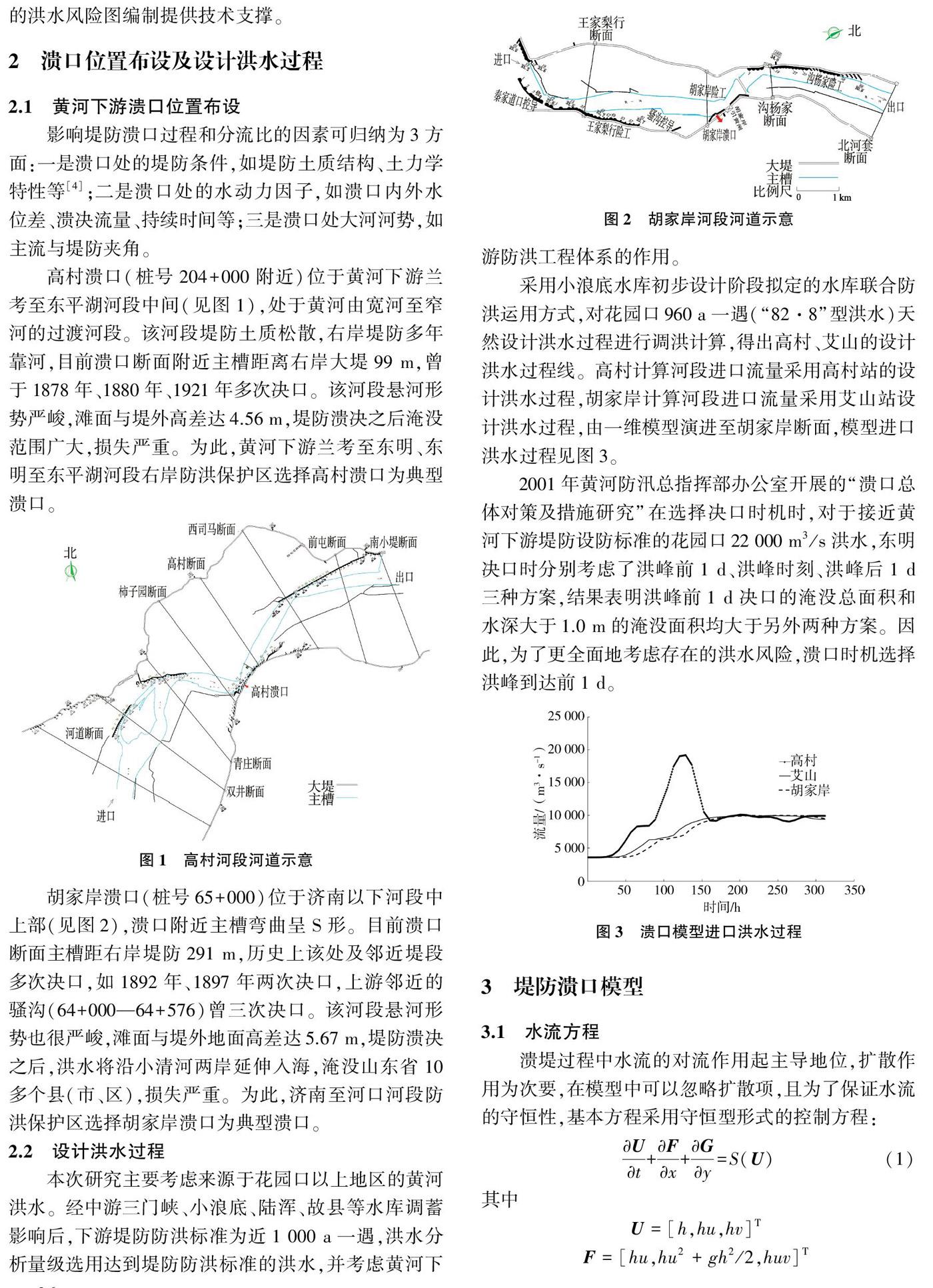
胡家岸溃口(桩号65+000)位于济南以下河段中上部(见图2),溃口附近主槽弯曲呈S形。目前溃口断面主槽距右岸堤防291 m,历史上该处及邻近堤段多次决口,如1892年、1897年两次决口,上游邻近的骚沟(64+000—64+576)曾三次决口。该河段悬河形势也很严峻,滩面与堤外地面高差达5.67 m,堤防溃决之后,洪水将沿小清河两岸延伸入海,淹没山东省10多个县(市、区),损失严重。为此,济南至河口河段防洪保护区选择胡家岸溃口为典型溃口。
2.2 设计洪水过程
本次研究主要考虑来源于花园口以上地区的黄河洪水。经中游三门峡、小浪底、陆浑、故县等水库调蓄影响后,下游堤防防洪标准为近1 000 a一遇,洪水分析量级选用达到堤防防洪标准的洪水,并考虑黄河下游防洪工程体系的作用。
采用小浪底水库初步设计阶段拟定的水库联合防洪运用方式,对花园口960 a一遇(“82·8”型洪水)天然设计洪水过程进行调洪计算,得出高村、艾山的设计洪水过程线。高村计算河段进口流量采用高村站的设计洪水过程,胡家岸计算河段进口流量采用艾山站设计洪水过程,由一维模型演进至胡家岸断面,模型进口洪水过程见图3。
2001年黄河防汛总指挥部办公室开展的“溃口总体对策及措施研究”在选择决口时机时,对于接近黄河下游堤防设防标准的花园口22 000 m3/s洪水,东明决口时分别考虑了洪峰前1 d、洪峰时刻、洪峰后1 d三种方案,结果表明洪峰前1 d决口的淹没总面积和水深大于1.0 m的淹没面积均大于另外两种方案。因此,为了更全面地考虑存在的洪水风险,溃口时机选择洪峰到达前1 d。
3 堤防溃口模型
3.1 水流方程
溃堤过程中水流的对流作用起主导地位,扩散作用为次要,在模型中可以忽略扩散项,且为了保证水流的守恒性,基本方程采用守恒型形式的控制方程:
式中:ρ′为河床淤积物干密度;α为恢复饱和系数;Ds为泥沙扩散系数;
Sk为第k组泥沙的含沙量;S*k为第k组泥沙的水流挟沙力;zbsk为第k组悬移质运动所引起的河床高程变化。
3.3 横向展宽
黄河下游堤防堤基为砂壤土、粉细砂与壤土、黏土相间分布,都属于黏性土的范畴。根据土力学边坡稳定性理论,溃口边坡土体的重力等因素在坡体内引起剪应力,当剪应力大于土体的抗剪强度时,就要产生剪切破坏,边坡土体发生失稳坍塌,溃口尺寸在横向扩大。Osman提出的黏性土体河岸展宽计算方法是建立在土力学分析基础上的,主要考虑冲刷和崩塌两部分。
(1)冲刷展宽过程计算。计算公式为
ΔB=ClΔt60(τ-τc)γse-1.3τc (4)
式中:γs为大堤(或河岸)土体的容重,kN/m3;ΔB为Δt时间内口门因水流侧向冲刷而后退的距离,m;Cl为冲刷系数,其值取决于土体特性;τ为作用在口门处的水流切应力,N/m2;τc为大堤土体的起动切应力,N/m2。
采用唐存本提出的黏性土起动拖曳力公式计算堤防土体的临界剪切应力:
τc=6.68×102×d+3.67×10-6d(5)
式中: τc为起动拖曳力,N/m2; d为土体颗粒粒径,m。
(2)崩塌过程计算。尽管黄河下游堤防土质属于黏性土的范畴,但土质松散,当溃口下部受到冲刷变宽、边坡变陡时,其上部必然发生坍塌,采用泥沙的水下休止角作为判断坍塌的临界条件[5]。
3.4 數值计算方法
采用Godunov型格式[6-7]的有限体积法(FVM)对控制方程进行离散。溃堤水流存在间断,属于黎曼问题,可用Godunov型格式求解黎曼问题从而得出数值通量。要构造准确的界面数值通量,需采用加权无震荡格式(WENO)构造出界面处高精度的守恒变量;还需要进一步采用Roe方法计算界面两边守恒变量跳跃量,从而求出界面数值通量,即流速和水深。时间项的离散采用三阶Runge-Kutta型离散格式。
3.5 边界处理
(1)进口边界:进口提供流量边界条件。
(2)出口边界:黄河干流出口提供水位流量关系边界条件;堤防溃口外的洪水演进区均为出口开边界条件,情况复杂,很难用流量过程、水位过程、水位流量关系等常规方法确定,因此按照自由出流考虑,即q/n=0。
(3)闭边界处理:采用直接镜像法,即在每个计算方向的边界处采用对称点处理法,假设对称点水深相同、流速相反,uR=-uL,hR=hL。
(4)时间步长: Δt=α′×min(Δx|u|+gh,Δy|v|+gh), α′为克朗数系数,一般在0.1~0.6之间取值。
4 成果分析
4.1 洪水演进过程分析
高村段堤防溃决发生时,河道内外水位差为4.5 m。口门区水流为急流,附近水流向溃口汇聚,漫过溃口后呈扩散状向堤外演进,溃口水流垂直于溃口。图4为溃决发生24 h时溃口流速分布。图4 高村溃口附近流场(溃决24 h)
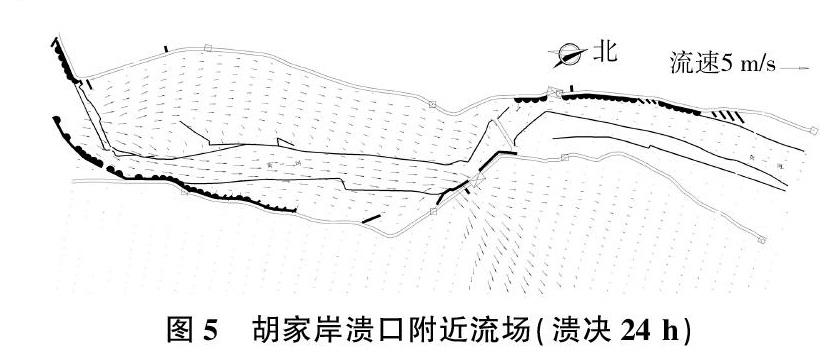
胡家岸段溃决发生时,河道内外水位差为5.6 m。相对于高村河段溃口,胡家岸溃口所处河岸更加弯曲,水流漫过溃口后主流流向略偏右侧。图5为溃决发生24 h时溃口流速分布。
4.2 溃口冲刷深度
图6为高村口门冲刷纵剖面示意,堤防溃决1 h后,河道内侧180 m、外侧200 m范围内河床冲刷,随后逐渐扩大。堤防溃决72 h后,紧挨口门的河道内侧500 m范围内河床发生明显的冲刷,尤其是200 m范围内河床下降超过7 m,口门处形成局部冲刷坑。
图7为胡家岸口门冲刷纵剖面示意,堤防溃决1 h后,河道内侧120 m、外侧150 m范围内河床冲刷,随后逐渐扩大。堤防溃决72 h后,紧挨口门的河道内侧400 m范围内均有很明顯的河床冲刷发生,尤其是100 m范围内河床下降超过8 m。
2001年,黄河水利委员会组织开展的“防汛抢险关键技术研究”项目中,黄河水利科学研究院完成了“口门区水力特性及冲刷特性模型试验”专题研究。模型试验结果表明:堤防决口后,溃决洪水在口门附近形成局部冲刷坑,位置基本在口门以下,随溃口展宽,溯源冲刷向堤内延伸。从高村、胡家岸口门纵剖面发展过程可以看出,溃决水流冲蚀口门处形成冲刷坑并不断扩大,与黄河水利科学研究院的物理模型试验结果基本一致。
4.3 溃口宽度变化
溃决时机为洪峰到达前24 h,该时刻作为统计分析的初始时刻,高村河段溃口展宽过程见图8。溃口宽度发展主要集中在前24 h,达到560 m。该时间段溃口处河道内外水位差较大,水流经溃口下泄的同时势能转化为动能,较大的流速造成水流的强冲刷力,溃口泥沙易被水流挟带走,溃口以较快的速度展宽。48 h后溃口宽度达到720 m,之后溃口处堤外水位升高后,两侧水位差减小,水流流速减小,对溃口泥沙的冲刷减弱,横向展宽速度减缓,计算结束时刻溃口宽度为900 m。
胡家岸河段溃口展宽过程见图9。前24 h溃口横向宽度发展速度较快,达到570 m,24 h以后展宽速度迅速减小,48 h溃口宽度为650 m,计算结束时溃口宽度为720 m。相对于高村河段溃口,胡家岸溃口处河道内外水位差较大,因此溃口初期展宽速度略快,但是洪水量级小于高村断面,受河道来流影响,稳定后溃口宽度较小。
4.4 溃口横断面变化
初始溃口宽度设为50 m,即将50 m长的堤防高程设为与滩面齐平,当堤内水位超过此处堤顶高程时,水流漫过此处,下切出一条深槽,随着水流冲蚀,堤防逐渐坍塌,溃口逐渐展宽。
高村溃口横剖面见图10。72 h溃口滩地降低最大为12 m,形状基本上还是中间较深、两侧较浅,接近矩形。由于左侧冲刷较快,因此口门轴线略偏左侧。
胡家岸溃口横剖面见图11。72 h溃口滩地降低最大为14 m,形状基本上还是中间较深、两侧较浅,接近矩形,轴线略偏左侧。
4.5 溃口流量变化及分流比
高村河段堤防溃决后各时刻的入流、决口出流、河道下游出流流量过程见图12。堤防溃决过程中,溃决流量变化过程为急速上升至峰值后缓慢下降,随后趋于稳定,河道下游河道流量持续下降,直至稳定。溃口分流比第1 d约为46%,第2 d约为70%,第2 d之后基本保持在80%左右。
胡家岸河段决口后口门各时刻的入流、决口出流、河道下游出流流量过程见图13。溃口流量变化受溃口发展的影响,溃决过程水流不断冲刷溃口,初期河道内外两侧水位差较大,溃口水流流速较大,对溃口冲蚀作用较强,溃口展宽速度也较快,前24 h溃口流量发展相应较快。随着河道两侧水位差减小,溃口流速减小,溃口展宽速度逐渐减缓,流量也相应减小,直至溃口发展达到稳定状态。溃口分流比第1 d约为50%,第2 d约为79%,第3 d约为71%,最终保持在75%左右。
在黄河水利委员会组织开展的“防汛抢险关键技术研究”项目中,北京大学开展了 “堤防溃口数学模型及口门区水流特性研究”专题研究[8],采用数学模型对东明口门1982年洪水进行了计算分析,结果认为分流比第1 d为40%~60%,第2至3 d为70~75%,第4 d为75%左右。根据历史资料分析,溃口宽度在800 m以下时,溃口分流比为70%~80%。因此,高村和胡家岸的分流比最终保持在80%和75%,说明模型计算结果是合理的。
5 结 论
(1)根据黄河下游现行河道堤防历时决口情况,结合下游堤防工程、河道特点、现行河势、溃决后淹没范围及社会经济生态影响等因素,黄河下游宽河段选取高村溃口为典型溃口,窄河段选取胡家岸溃口为典型溃口。
(2)建立了堤防溃口模型,对高村和胡家岸河段右侧堤防溃决过程进行了数值模拟,高村口门溃决后水流垂直于堤防向堤外漫流,胡家岸口门溃决后水流流向偏右,与堤防呈一定交角。高村口门处形成局部冲刷坑,堤内外200 m范围冲刷明显,河床下降最大处超过7 m。胡家岸口门处堤内外100 m范围冲刷明显,河床下降最大处超过8 m。
(3)高村溃口前24 h展宽迅速,24 h溃口宽度达到560 m,48 h溃口宽度达到720 m,最终溃口宽度为900 m。胡家岸溃口24 h溃口宽度为570 m,48 h溃口宽度为650 m,最终宽度为720 m。高村河段洪水量级大于胡家岸河段的,但溃口处堤防两侧高差小于胡家岸河段的,因此胡家岸口门前期展宽快,但最终宽度小于高村口门宽度。
(4)高村、胡家岸口门横断面形状接近矩形,中间较深,两侧略浅。高村河段堤防溃决后,溃决流量为急速上升至峰值后缓慢下降,随后趋于稳定,河道出口流量持续下降,直至稳定。溃口分流比第1 d约为46%,第2 d约为70%,第2 d之后基本维持在80%左右。胡家岸河段决口前24 h溃口流量发展较快,溃口分流比第1 d约为50%,第2 d约为79%,第3 d约为71%,最终保持在75%左右。
参考文献:
[1] 翟家瑞,张素平,丁大发.黄河溃堤溃口对策研究[J].人民黄河,2003,25(3):3-4.
[2] 丁大发,汪习文,韩侠,等.黄河下游溃堤洪水灾害与减灾对策研究[J].人民黄河,2003,25(3):22-25.
[3] 张素平,翟家瑞,祝杰,等.黄河溃堤对策研究的内容及途径分析[J].人民黄河,2003,25(3):16-17.
[4] 梁林,倪晋仁.黄河溃堤过程数学模型及其模拟方法[J].中国科学(E辑),2002,32(5):618-627.
[5] 贺治国,WU Weiming.考虑水沙相互作用的河堤溃决二维数值模拟[J].水动力学研究与进展,2010,25(2):147-154.
[6] 梁艳洁.非黏性土堤漫顶溃决冲蚀过程及水力学机理研究[D].武汉:武汉大学,2009:46-47.
[7] 徐国宾,孟庆林,苑希民.含沙溃堤洪水数值模拟分析[J].天津大学学报(自然科学与工程技术版),2016,49(10):1008-1015.
[8] 梁林.黄河溃堤过程数学模型及其模拟技术研究[D].北京:北京大学,2002:26-27.
【责任编辑 许立新】
收稿日期:2018-11-26
基金项目:国家重点研发计划项目(2016YFC0402503)
作者简介:梁艳洁(1984—),女,河南洛阳人,高级工程师,博士,研究方向为水力学及河流动力学
E-mail:iamlyj_2006@163.com

