级配特征和水力梯度对砂砾料渗透性影响研究

梅世昂 钟启明 陈澄昊 阎志坤

摘 要：为探索砂砾料渗透性的规律，开展了室内垂直向上渗透试验，结果表明，砂砾料渗透性随着孔隙比的增大而增强，随着细粒含量的增高而减弱。对特征粒径进行了进一步推导，给出了连续级配的特征粒径计算方法，通过量纲分析和参数拟合，得到砂砾料渗透系数的经验公式。通过渗透变形试验，将水力梯度对砂砾料渗透性的影响进行了分析，结果表明：细粒含量高，则渗透系数随水力梯度的增大而增大;细粒含量低，则渗透系数随水力梯度的增大而减小。结合细粒含量、孔隙比的影响，给出了考虑水力梯度的渗透系数计算公式，并对试验结果进行验证，结果表明，该公式可较好地反映各参数，尤其是水力梯度对渗透性的影响，拟合效果较好。

关键词：砂砾石料;特征粒径;渗透系数;水力梯度

中图分类号：TV222.2文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.06.026

Research on the Influence of Gradation Characteristics and Hydraulic Gradient on

Permeability of Sandy Gravel Material

MEI Shiang1， ZHONG Qiming1，2， CHEN Chenghao1，YAN Zhikun1

（1.Nanjing Hydraulic Research Institute， Nanjing 210029， China;

2.Key Laboratory of Failure Mechanism and Safety Control Techniques of Earth-Rock Dam of the Ministry of

Water Resources， Nanjing 210029， China）

Abstract： Laboratory vertical upward permeability tests were carried out to study the permeability of sandy gravel material. The results show that the permeability of sandy gravel increases with the increase of void ratio and decreases with the increase of fines content. The characteristic particle sizewas further deduced and the calculation method of the continuous grading characteristic particle size was given. Then combining dimensional analysis and parameter fitting， the empirical formula model of permeability coefficient of sandy gravel was obtained. Furthermore， the influence of hydraulic gradient to the permeability of sandy gravel was studied and analyzed through the permeability deformation test. The results show that when the content of fine particles is high， the permeability coefficient increases with the increase of hydraulic gradient， whereas when the content of fine particles is low， the permeability coefficient decreases with the increase of hydraulic gradient. Combined with the influence of fines content and void ratio， the permeability coefficient model considering hydraulic gradient was given and the test results were verified. The results show that the model can fairly reflect the influence of various parameters， especially the hydraulic gradient on the permeability， with a good fitting effect.

Key words： sandy gravel; permeability coefficient;characteristic particle size;hydraulic gradients

1 研究背景

砂礫料压实后具有强度高，颗粒破碎率低，流变小，且综合单价低的优点，被广泛用于土石坝建设中[1]，但天然砂砾料往往级配较宽，细颗粒含量高，级配离散性差，作为坝体主要材料其渗透稳定性尤其需要关注。

鉴于渗透性的重要性，许多学者对渗透性的影响因素进行了分析，认为渗透系数不仅取决于岩石的性质（如粒度成分、颗粒排列、充填状况、裂隙性质及其发育程度等），而且与渗透液体的物理性质（容重、黏滞性等）有关[2]，并在此基础上提出了渗透系数的经验模型。对于砂砾料，其渗透特性主要与其结构有关，这在制样时，主要取决于其试验级配、试验孔隙比和制样方式。用于表征颗粒级配的参数很多，包括不均匀系数Cu、曲率系数Cc、控制粒径di等，di是级配曲线中小于某粒径含量占总质量百分比所对应的粒径。太沙基等[3]就用d10来表征级配，即小于该粒径的颗粒含量占总质量的10%，发现渗透系数与d10的平方成正比，进而提出了渗透系数的经验公式，更多的学者在此基础上对表征粒径进行优化[4～7]，提出新的经验公式，将d50、d30、d20、d17、d9等作为表征粒径，见表1。

但是，这些公式无法反映整体级配情况，提出的经验公式往往也只针对特定的试验土样，缺乏普适性，计算效果也不是特别理想。也有部分学者通过试验给出不均匀系数和曲率系数对砂土渗透性的影响，但得到的结论却不尽相同。任玉宾等 [8]、张国栋等[9]发现钙质砂和碎石土渗透性随不均匀系数的增大而增强，但随曲率系数的变化规律则完全相反;杨兵等[10]、樊贵盛等[11]、宿辉等[12]、刘一飞等[13]发现砂砾土渗透系数随不均匀系数的增大而减小;苏立君等[7]将不均匀系数、曲率系数引入渗透模型，但本质上其模型中CcCud210可直接化简为d230，渗透系数还是与控制粒径的平方成正比。种种研究均表明，在渗透性研究中不均匀系数和曲率系数并不能很好地代表颗粒级配的影响。

另一部分学者认为土体渗透性主要受其中细颗粒含量影响，这时需要区分粗细颗粒界限，一般工程中将5 mm作为粗细颗粒的分界线，认为土体渗透性主要与其小于5 mm的细颗粒含量有关，用P5表示，当细颗粒含量超过40%时土体渗透稳定性较好。刘杰等[14]将几何平均粒径dq=d70d10作为粗细颗粒区分粒径，又通过对代表性试验资料的反演计算，认为对多级配土，将2 mm作为粗细颗粒的分界线较为合理。此外，也有将1.000、0.063 mm作为粗细颗粒区分粒径，但是至今粗细颗粒区分粒径还没有统一标准，而且也很少会在渗透模型中引入细粒含量的概念。

坝料级配设计是筑坝工程中控制坝料渗透性的最主要途径之一，笔者通过砂砾料向上垂直渗透试验，进行不同孔隙比和不同级配的砂砾料渗透试验，研究分析各级配特性对渗透性的影响，给出控制砂砾料渗透性的主要级配特征，通过回归分析，得到砂砾料渗透系数经验公式。

目前，在渗透系数的影响因素研究上对水力梯度影响的研究较少。王沛等[15]、宋林辉等[16]进行了不同水力梯度下的黏土渗透试验，认为水力梯度对渗透系数的影响主要在于水压的固结作用。王福刚等[17]对粗砂、中砂、细砂进行不同水力梯度下的水平渗透试验，对水力梯度的影响进行了定性描述，发现粗砂所受影响最大。对于连续宽级配砂砾料渗透性受水力梯度的影响则较少有人研究。砂砾料试验求解渗透系数一般认为基于达西定律，渗透系数不随水头的改变而改变。但是，通过试验发现水力坡降与渗透系数不一定是线性关系，随着水头的提高，土體在达到临界水力梯度前，测得的渗透系数会有些许变化，存在幂函数或二次函数的关系。这是土体中的颗粒，特别是细颗粒在渗透力的作用下会发生偏转或移动，土体会进行部分颗粒重排列，进而导致土体结构的变化和孔隙通道的变化，影响整体渗透性。而在恒定水头作用时，粗粒料颗粒在完成重排列后渗透水的流量往往趋于稳定，也就是说，在恒定水头作用下，可以用渗透系数来真实反映土体渗透性，这样通过研究水头和渗透系数的关系，就可以给出任意水头下土体的渗透系数来真实反映在相应水力梯度作用下土体稳定后的渗透性。

2 试验方案及结果

试验所用试样为西藏某坝筑坝所用的天然砂砾料，见图1。

试样岩性以中细砂岩为主，其次为板岩、石英岩、花岗岩等，砂为中细砂，其主要成分为石英、长石、云母等。试验在大型垂直渗透仪上进行，试样直径为300 mm、渗径300 mm。受试样尺寸限制，试验级配最大粒径不超过60 mm，为满足试验要求，试验级配是由坝料实际设计级配通过缩尺得到，缩尺方法为等效替代法和相似级配法相结合的混合方法。相似级配法保持了级配关系（不均匀系数不变），细颗粒含量提高，但不应影响原级配的力学性质，一般来讲，小于5 mm颗粒含量为15%～30%;等效替代法具有保持粗颗粒的骨架作用及粗料的级配的连续性和近似性等特点，适用超粒径含量小于40%的堆石料。缩尺后5组（C1、C2、C3、C4、C5）级配曲线如图2所示。

根据试验要求的干密度、试样的尺寸和级配曲线计算所需试样质量，试验所用的试样均处于自然风干状态，分60～40、40～20、20～10、10～5、5～1、1～0.5、0.5～0 mm共7种粒径范围进行试样的称取。装样时在仪器壁内侧涂以凡士林，以避免沿仪器壁集中渗漏，试样采用振动击实法分三层进行装样，在控制试样干容重的同时严格控制装样时产生颗粒离析，采用水头饱和法逐级进行饱和。

试验采用常水头法，水流方向从下向上，共进行了5组级配的渗透试验和渗透变形试验。装样时，通过干密度控制孔隙比，尽量保证试样均匀性，减小振动击实过程中的颗粒析出。其中C3、C4和C5级配试样在2种孔隙比下进行试验，分别为0.232和0.199;而C1、C2级配试样在孔隙比0.204下进行试验。试样成型后采用从下向上滴水饱和法使其饱和，试样饱和历时12 h以上，在水流和测压管水位稳定后，测定一定时间内的排水量，同时测定进、出水的温度。按达西定律计算渗透系数：

k=QLAhT

式中：k为渗透系数，cm/s;Q为时间t内的渗透水量，cm3;L为两测压孔中心间的试样高度，cm;A为过水断面面积，cm2;h为平均水位差，cm;T为时间，s。

试验条件及结果见表2。

从表2可以看出：孔隙比越大，砂砾料的渗透系数也就越大。渗透水在颗粒孔隙形成的孔隙通道中流动，孔隙比越大，意味着形成的孔隙通道越多，渗透水的过流面积也越大，相应的渗透流量也就越大。总体渗透性C2、C5>C4>C1、C3，可以看出，级配曲线越在上方，也就是细粒含量越高，渗透性越差。在相同孔隙比下，细粒含量越高，意味着土体排列结构越紧密，有更多的细颗粒堵住孔隙通道，渗透性也就越差。

3 试验结果分析

通过量纲分析，渗透系数k可写作：

k=ηρgμd2（1）

式中：η为与土体本身性质有关的系数;ρ为渗透液体的密度;g为重力加速度;μ为渗透液体动力黏度;d为颗粒粒径。

对渗透系数经验公式来说，控制粒径的选取对于计算效果起到关键性的作用。选取颗粒特征粒径d0作为控制粒径[19]，1d0=∑pidi，其中pi是每个粒组粒径di颗粒质量占总质量的百分比。对于连续级配，可认为每个粒组的粒径在这段范围内均匀分布，再确定最小粒径dmin，则特征粒径可写作：

1d0=∑∫di+1diPididd=∑Pi+1-Pidi+1-diln（di+1di）（2）

式中：di、di+1分别为所选粒组的最大、最小粒径;Pi、Pi+1分别为小于粒径di、di+1颗粒质量占总质量的百分比。

选取C3、C4、C5级配试样在0.232和0.199两个孔隙比下的渗透试验结果，发现其渗透系数与级配特征粒径的二次方有很好的线性正相关性，如图3所示。

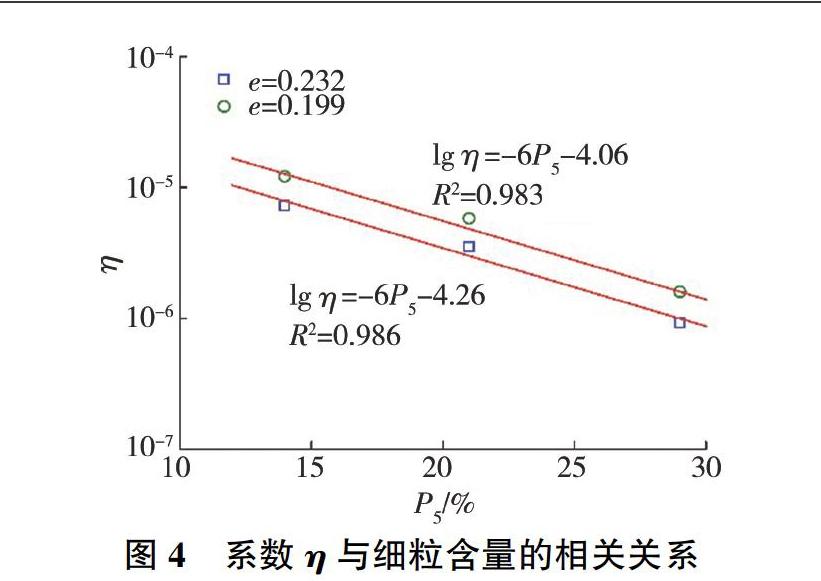
基于规范和方便工程应用的原则，将小于5 mm的颗粒含量P5作为试验的细粒含量，细粒含量和孔隙比一起决定了土体中颗粒排列结构，从表2中的试验结果可以发现，细粒含量越高，孔隙比越低，其渗透性越差。在式（1）中的渗透特性系数η就是用于反映土体本身性质，η与细粒含量P5和孔隙比e的关系如图4所示。

从图4可以看出，η的对数与P5呈线性负相关，即细粒含量越高渗透特性系数越小;孔隙比越大渗透特性系数也越大。此外，两组数据的拟合斜率都近似为-6，意味着不同孔隙比下lg η受到P5的影响程度是相似的，所以可以将细粒含量P5和孔隙比e作为自变量，lg η作为应变量进行线性回归，得到渗透特性系数的经验公式：

lg η=-6+8e-6P5（3）

代入式（1）有：

k=10-6+8e-6P5ρgμd20（4）

当渗透溶液为20 ℃水时，ρgμ≈107，式（4）也可写成：

k=101+8e-6P5d20（5）

将计算结果与试验结果对比，如图5所示。

其中，C2的计算值与试验值相对误差最大，为57%，其余相对误差均在40%以内，对于渗透系数来说，误差均在合理范围内，说明此渗透系数经验公式计算效果较好。

4 考虑水力梯度的渗透试验

一般情况下，对于砂砾料，如果不考虑水力梯度对颗粒重排列的作用，依据达西定律，渗透系数应该不随水头的变化而发生改变。但实际上，在垂直向上的渗透变形试验中，随着水力梯度的增大，到破坏水力梯度为止，渗透系数出现了一定的变化，将之前5组试样逐级提高水头，并在水头稳定后测得出渗流量，进而计算出渗透系数，得到的渗透系数随水力梯度i变化得关系如图6所示。

从图6可以发现，在发生破坏前渗透系数k随着水力梯度的增大，或增大（C1），或减小（C2、C4、C5），或基本保持不变（C3）。这种结果上的差异主要是细颗粒含量的不同。水力梯度对渗透系数的影响一方面是细颗粒在渗透力的驱动下在孔隙管道中发生移动，可能会在通道中相聚堵塞孔隙通道;另一方面，细颗粒流失后，粗颗粒骨架进行再排列，达到新的平衡状态。对于C1，细粒含量（P5=42.3%）很高，意味着细颗粒可以完全充满粗颗粒骨架孔隙，细颗粒与粗颗粒紧密排列，部分细颗粒甚至承担土体骨架的任务，若这部分细颗粒在渗透力的作用下发生移动，使得周围颗粒需要进行再排列达到新的平衡，这一过程会引起孔隙通道的增多。此外，随着水力梯度的增大，渗透力增大，则有更多的承力细颗粒发生移动。所以，其渗透系数随着水力梯度的增大而增大。

当细粒含量较为适中时如C3，P5=29%，土体结构稳定，在达到临界水力梯度前，土体结构基本保持稳定，渗透系数随水头的增大变化不大。

对于细粒含量相对较少的C2、C4和C5试样，在达到临界水力梯度前，无明显细颗粒析出，细颗粒在渗透力的作用下，在孔隙管道运动聚集并堵塞淤积，形成自反滤层，造成过水面积的减小，进而土体渗透性变差。

考虑水力梯度对渗透系数的影响，在式（4）的基础上引入修正参数t，修正渗透系数可表示为k=tk0，t为与水力梯度相关的参数;k0为初始渗透系数，反映不考虑水力梯度初始试样本身的渗透性。因土体在低水头时可近似当作渗透系数不变，可将渗透试验所得渗透系数作为k0。在本文中即用表2中渗透系数作为k0。但是，在后续拟合计算时C1渗透变形试验初始渗透系数与表2中有些差距，故用最低水力梯度时的渗透系数作为k0。

当i=0时，k=k0，从图6可以看出，渗透系数随水力梯度的变化除了C3变化不大，其他都可以用线性形式基本描述，所以有：

t=αi+1（6）

式中：α为修正系數与水力梯度间的相关系数;i为水力梯度。

经拟合发现α为关于孔隙比和细粒含量的函数，α=0.5e+P5-0.4，代入式（6）有：

t=（0.5e+P5-0.4）i+1（7）

这也给出了水力梯度对渗透系数影响的判定方式，当α>0 时，即e+2P5>0.8，渗透系数随水力梯度的增大而增大;反之，当e+2P5<0.8，渗透系数随水力梯度的增大而减小。

代入式（5）有：

k=[（0.5e+P5-0.4）i+1]k0（8）

k0可直接根据式（4）或式（5）进行估算。

利用图6中的试验结果进行验算，计算值与试验值对比见图7。除了C2计算值平均相对误差超过了25%，最大相对误差达到53.1%，其他试样计算值平均相对误差均在10%左右。总体来说该模型计算效果较好，误差在可控范围内，能较好地反映水力梯度对渗透系数的影响，可为工程建设提供参考。

5 结 论

通过不同级配不同孔隙比砂砾料垂直向上的渗透试验得到以下结论：

（1）渗透试验结果表明，砂砾料渗透性随着孔隙比的增大而增强，随着细粒含量的提高而减弱。对特征粒径进行了进一步推导，给出了连续级配的特征粒径计算方法，通过量纲分析和参数拟合，得到砂砾料渗透系数的经验公式，该公式可较好地反映特征粒径、孔隙比和细粒含量对砂砾料渗透特性的影响。

（2）通过渗透变形试验，发现水力梯度对渗透系数具有一定的影响，是正影响还是负影响则与颗粒级配尤其是细粒含量有关。细粒含量较高时，颗粒排列较为紧密，细颗粒承担一部分骨架作用，随着水头的增大，部分细颗粒发生偏转或移动，形成更多的孔隙通道，渗透系数增大;当细粒含量相对较低时，在发生破环前，细颗粒发生重排列，在靠近出口面形成较为紧密的结构，整体渗透性变差，渗透系数减小。

（3）结合细粒含量、孔隙比的影响，给出了考虑水力梯度的渗透系数计算公式，并对试验结果进行验证，结果表明，此公式可较好地反映各参数，尤其是水力梯度对渗透性的影响，拟合效果较好。

参考文献：

[1] 陈生水，凤家骥，袁辉.砂砾石面板坝关键技术研究[J].岩土工程学报，2004，26（1）：16-20.

[2] 吴吉春，薛禹群.地下水动力学[M].北京：中国水利水电出版社，2009：14-17.

[3] 太沙基，帕克.工程实用土力学[M].北京：水利电力出版社，1960：32-38.

[4] HAZEN A. Discussion of “Dams on Sand Foundation” by A.C. Koenig[J]. Transactions American Society of Civil Engineers， 1911，73： 199-203.

[5] 刘杰.土的渗流稳定与渗流控制[M].北京：水利电力出版社，1992：3-16.

[6] CARMAN P C. Fluid Flow Through Granular Beds[J]. Transactions of the Institution of Chemical Engineers， 1937，15：150-167.

[7] 苏立君，张宜健，王铁行.不同粒径级砂土渗透特性试验研究[J].岩土力学，2014，35（5）：1289-1294.

[8] 任玉宾，王胤，杨庆.颗粒级配与形状对钙质砂渗透性的影响[J].岩土力学，2018，39（2）：491-497.

[9] 张国栋，廖爱明，李泯蒂，等.碎石土渗透特性试验研究[J].水利水运工程学报，2016（5）：91-95.

[10] 杨兵，刘一飞，万奋涛，等.级配特性对砂土渗透系数影响试验研究[J].西南交通大学学报，2016，51（5）：855-861.

[11] 樊贵盛，邢日县，张明斌.不同级配砂砾石介质渗透系数的试验研究[J].太原理工大学学报，2012，43（3）：373-378.

[12] 宿辉，王晓伟，石明宇.砂砾土孔隙特征对渗透系数的影响研究[J].河北工程大学学报（自然科学版），2013，30（4）：82-86.

[13] 刘一飞，郑东生，杨兵，等.粒徑及级配特性对土体渗透系数影响的细观模拟研究[J].岩土力学，2019，40（1）：1-10.

[14] 刘杰，张雄.多级配砾石土反滤设计方法试验研究[J].岩土工程学报，1996，18（6）：5-13.

[15] 王沛，石磊，姚远宏.不同渗透压力条件下黏质粉土的渗透试验研究[J].土工基础，2018，32（5）：567-570.

[16] 宋林辉，黄强，闫迪，等.水力梯度对黏土渗透性影响的试验研究[J].岩土工程学报，2018，40（9）：1635-1641.

[17] 王福刚，张佳慧，于吉洋，等.不同水力梯度对渗透系数影响研究[J].实验技术与管理，2015（6）：25-28.

[18] 明滋，舒别尔特.粒状材料水力学[M].北京：水利出版社，1957：6-13.

【责任编辑 赵宏伟】