坡体渗流与气温变化相关性分析

刘刚+童富果+习念念+郝霜

摘要：基于多相流及多场耦合理论，采用有限单元法计算了三峡库区木鱼包滑坡体温度随气温变化情况，进而依据温度与水体黏滞性的相关关系分析气温变化对坡体渗流的影响。计算表明，坡内温度受气温影响仅限于坡体浅层区域，距地表深度越深，影响程度越小，在时间上的滞后性越大。温度变化可改变水的黏滞性，进而引起土体渗透参数的改变，计算表明因气温变化引起的坡体渗透性改变较为显著。坡体渗透系数受气温变化的影响随深度呈非线性分布，距地表越深受气温变化的影响越弱，通常大于雨水最大入渗深度以后，坡体渗透系数不再发生显著变化。另外，坡体渗透系数随气温呈现季节性变化规律，夏季气温高于坡内土体温度，渗透系数随深度的增加而减小；冬季坡体内温度高于气温，渗透系数随深度的增加而增加。

关键词：气温；渗透系数；坡体渗流；多相流；季节性

中图分类号：TV223.4 文献标识码：A 文章编号：1672-1683（2017）03-0158-06

Abstract：Based on the multi-phase flow & multi-field coupling theory，this paper adopted the finite element method to calculate the temperature distribution of Muyubao landslide as the atmospheric temperature changes.Further，it analyzed the influence of atmospheric temperature changes on the slope seepage according to the correlation between temperature and viscosity of water.The results of calculation showed that the effect of atmospheric temperature on temperature of the slope body is limited to the shallow surface；as the depth increases，the influence decreases and the hysteresis increases concurrently.The mobility of the water is affected by the change of the slope body′s temperature and it can change the water permeability in the inner slope.The effect of atmospheric temperature on permeability coefficient of the slope has a nonlinear relationship with depth.The effect of atmospheric temperature on the permeability coefficient declines as the depth increases.Generally，the permeability coefficient of the slope no longer change significantly when the depth is deeper than the maximum depth of infiltration.The permeability coefficient of the slope shows seasonal variation with the atmospheric temperature.The permeability coefficient decreases with the increase of depth when the atmospheric temperature is higher than the soil in summer.In contrast，the permeability coefficient increases with the increase of depth in winter.

Key words：air temperature；permeability coefficient；slope seepage；multiphase flow；seasonal

坡体渗流通常属于非饱和渗流的范畴，涉及到土（石）、水、气组成的多相物质的耦合作用[1]。坡体渗流通常与坡内水体渗透性、坡体初始含水率、渗透边界等诸多因素有关[2-3]，其中水体渗透性是影响坡体渗流的关键因素之一。水在土体中的渗透性主要受水的黏滞性、相对饱和度以及土体本征渗透性的影响[4]，而气温变化对土体本征渗透性以及相对饱和度的影响较小，因此气温变化主要通过改变水的黏滞性来影响坡内水体渗透性。在坡体温度场方面，许多学者做了大量研究并取得了丰硕的成果[2，5-10]。然而，较多研究者在计算坡体温度场时仅考虑了热量在土体中的传导，未考虑水、热耦合的热传输作用，导致坡体温度场计算结果不准确[11-12]。此外，部分研究者未能基于气温引起的坡体温度改变结果进一步计算其对坡内水体渗透性的影响[13-14]，常因温度变化不显著而得出气温变化对坡体渗流无影响的结论。本文基于多相流及多场耦合的理论和方法，完整地考虑了热传导、热传输及水热耦合效应，准确模拟坡体温度场分布，定量分析气温变化对坡内水体渗透性的影响。

1 計算模型

1.1 水、气、热传输控制微分方程

依据连续介质力学的基本理论及方法，将土体视为是由气、液、固三相介质组成的连续体，其内部水、气、热的传输在数学上可表述为基于时间和空间的偏微分方程描述。水（液相）在土体中的流动主要源于水压力梯度驱动，并受土体孔隙率、土体含水量以及水的黏滞性等因素影响，基于液态水的质量守恒可导出土体内水流动的控制微分方程[14]：

上述三个方程是基于时间和空间的非线性偏微分方程组，求解时需对其进行时间和空间离散。本文空间离散采用Garlerkin有限单元法，时间离散采用差分法。以孔隙气压Pg、水饱和度Sl以及温度T为未知量，通过对水、气、热三个方程的循环迭代计算实现每个时间步内非线性方程组的求解。

1.2 本构模型及参数

计算所涉及的本构关系主要包括土水特征曲线、水的相对渗透系数、气的相对渗透系数以及土体热传导系数等，具体模型及其参数表述如下。

（1）土水特征曲线。土水特征曲线是用来描述非饱和土体强度与渗透特性的关系曲线，本文采用常用的Van Genuchten模型[16-17]，可表述为基质吸力与饱和度之间的函数关系：

（4）水、气粘黏滞系数。水、气黏滞性的大小与温度、压强等因素有关，在边坡降雨过程中，黏滞系数随压强变化不大，温度是影响黏滞系数大小的主要因素，由Guvanasen and Chan模型[21-22]可得水、气黏滞系数为

式中：λs、λw、λg分别为固、液、气三相各自的热传导系数，其值分别为λs=3.20，λw，=0.58，λg=0.024，（单位：W/（m·℃）。η1、η2为模型参数，其中η1可表示为孔隙率的函数，其值可表示为η1=0.0692n-0.7831，η2可由孔隙率及饱和度表示出来，η2=0.59S1.487n-0.0404l。

此外，计算涉及到的主要参数为孔隙率n=0.35，土体本征渗透性k=4.0×10-12m2，重力加速度g=9.8 m/s2，气体密度ρg=1.29 kg/m3，液相密度ρl=1×103 kg/m3，固体、液体、气体的比热容分别为cs=2 080，cl=4 183，cg=1 004（单位：J/（kg·℃））。

1.3 几何模型

木鱼包滑坡位于长江右岸，距三峡大坝坝址56 km，地属湖北省秭归县沙镇溪镇范家坪村。木鱼包滑坡前缘高程135 m，宽约1 450 m，剪出口位于滑坡后缘北段，最高标高520 m，东侧大乐沟大体近南北向延伸，长约620 m，西侧边界基本沿鹅卵石沟延伸，约1 200 m，后缘滑壁平直光滑，长约数百米。木鱼包滑坡体表层为松散堆积层，下层为扰动破坏的层状石英砂岩岩体。选取木鱼包滑坡体主滑动剖面为研究对象，采用二维平面渗流模型，沿坡体纵向取1 500 m，竖直向取600 m。对坡面进行有限元网格剖分时，为更好的模拟坡表降雨入渗，坡体表层区域采用较小网格，最小网格厚度约为0.25 m。最终计算网格共计2 033个单元和1 971个节点，见图1。

1.4 边界及初始条件

边界条件可分为渗流边界条件和温度边界条件。对于水气流动，滑坡体后缘侧面及底部均为不透水边界，其边界水压力及其变化可由计算得到。坡体前缘侧面位于库水位以下，为已知水头边界。水面以上为降雨入渗边界，降雨强度据三峡库区多年平均降雨资料得出（图2）。对传热过程而言，滑坡体后缘侧面设为不透热边界，底部边界受气温影响较小，温度相对稳定，计算中设定为20 ℃。坡表为已知温度边界，其中库水位以下部分的温度等于水温，水位以上部分的温度等于气温，并随气温变化（图3）。

渗流及温度初始条件涉及到饱和度和温度的数值大小及其空间分布，通常难以准确给出。为获取较为合理的渗流及温度初始条件，本分析在等温场、等饱和度条件下，结合三峡库区多年实测降雨及气温情况进行长时间模拟计算，以计算所得渗流场及温度场作为本研究的初始条件。2 气温与坡体渗流的相关性分析

坡内水体渗透性主要由土体孔隙大小及其特性决定，同时也受土体变形、土壤含水量、水的黏滞性等因素的影响。温度变化对坡内土体孔隙特性影响较小，而对坡内水体的黏滞性影響较为显著，因此，本节先分析气温变化对坡体温度的影响，然后研究由坡体温度改变引起的黏滞性变化，进而研究气温变化对坡内水体渗透性的影响。

2.1 气温对坡体温度的影响

在考虑水、热耦合作用的水气二相流计算中，基本变量主要有孔隙气压力、饱和度以及温度，在每一个时间步计算结束后均能得到对应时刻坡体内各基本变量的值，计算域内某一时刻坡体温度场分布情况见图4。由图4可知，坡体温度变化剧烈的区域主要集中在坡体表层，坡体内大部分区域的温度维持在20 ℃。

坡体温度变化与气温季节性变化特性密切相关。通过坡体温度全年的变化情况（图5）可知，坡体温度变化与气温变化具有相同的趋势，但在时间上具有一定的滞后性。例如全年最低气温出现在12月18日，而坡体不同深度处的最低温度均要晚于该时间。通过比较可以发现冬季的滞后性较夏季明显，这主要与冬季降雨量较少，坡体的温度变化主要由土体的热传导作用引起有关。由于夏季降雨充沛，雨水入渗引起的热传输作用占主导地位，因此坡体温度对气温变化较敏感，滞后性较冬季小。

由热传递的规律可知，热量总是由温度高的地方向温度低的地方传递。当外界气温高于坡体温度时，热量向坡体内传输，夏季坡体温度均低于气温，而冬季则呈现出坡体内温度高于外界气温的现象。距地表深度越深，气温变化引起的温度改变量越小。坡体内温度变化量通常小于气温改变量，在地下0.5 m处的变化幅度可达20 ℃，达到一定深度后，坡体温度不再随气温变化而发生改变，且波动小于1 ℃。可见气温变化对坡体的影响范围通常限于坡体浅层区域（约5～10 m左右），具体的深度与土体的孔隙率、含水量、降雨入渗边界等因素有关。

2.2 坡体温度对坡体渗流的影响

坡体渗流主要受坡内孔隙特性以及坡内水体流动性的影响，而往往温度变化对均质坡体内的孔隙影响较小，因此温度变化主要通过改变坡内水体流动性从而影响坡体渗流。水的黏滞性与温度的关系可根据公式（7）得出[21]，通过计算可知水的黏滞性受其温度影响较为显著，如水温5 ℃与35 ℃相比，黏滞性相差接近一倍（图6）。

式中：k为土体本征渗透性；μl为水的粘滞系数；klr为水的相对渗透系数。

为了便于比较，以20 ℃时的渗透系数为基准，计算各点渗透系数的相对变化量ω，图7为坡体中段某一竖向剖面上控制点的渗透系数相对变化量ω的全年变化情况。坡体渗透系数与坡体温度呈现相同的变化趋势，具有明显的季节性变化规律，且由于时间上滞后性的存在，坡体内不同深度处的渗透系数并不在同一时刻取得极值。根据式（10）可知，在坡体饱和度一定的情况下，坡体温度越高，水的黏滞性越小，坡体的渗透系数越大。距地表深度大于5 m以后，渗透系数不再随时间发生较大变化，这跟雨水入渗的最大深度相一致[25-26]，最大入渗深度以上既有土体对温度的传导作用又有水、热耦合的传输作用，而最大入渗深度以下仅有土体的热传导作用。

选取夏季和冬季具有代表性的几天，对坡体内不同深度处渗透系数的分布情况进行分析。由图8可知渗透系数在沿深度向上的变化并非是线性的，随深度的增加，渗透系数逐渐增加（或减小）并最终趋于稳定。当气温高于坡体内温度时（5月-6月），随距地表深度的增加渗透系数不断减小；反之，当气温低于坡体内温度时（10月-11月），渗透系数随距地表深度的增加而增加。

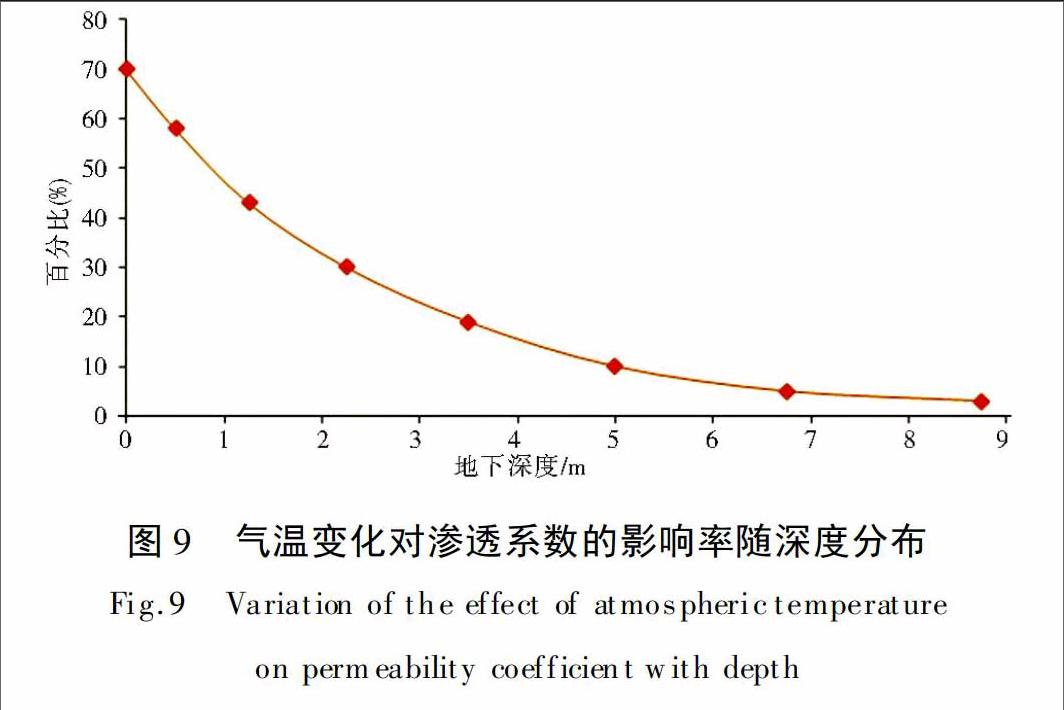
坡体不同深度处的渗透系数受气温影响的程度不同，将渗透系数相对变化量ω在全年的波动幅度定义为影响率。图9为气温变化对渗透系数的影响率随深度分布图，在地下1.25 m深度处，由气温变化引起的渗透系数变化量可达43%。随着深度的增加，气温变化对渗透系数的影响率越来越小，当深度为8.75 m时不同季节渗透系数的变化幅度不足3%，可认为气温变化对木鱼包滑坡体的影响深度在这一范围内。

3 主要结论

本文基于水气二相流基本原理，考虑热量在土体中的传导以及水、热耦合的传输作用，准确计算坡体内温度场分布，定量分析气温变化对坡体渗透系数的影响，从而研究气温变化与坡体渗流的相关关系。结果表明，气温变化对木鱼包滑坡体渗流的影响深度在地表以下10 m左右，坡体渗透系数随深度呈非线性分布，其变化率随深度的增加而减小，并最终趋于稳定。坡体渗透系数随气温呈现季节性变化规律，但在时间上具有一定的滞后性，深度越深滞后性越明显。夏季坡体渗透系数通常大于冬季，故在相同降雨条件下，夏季降雨入渗的深度更深、强度更大，由此引起土体抗剪强度减小，不利于边坡稳定，因此，夏季降雨更易导致滑坡。

参考文献（References）：

[1] 胡冉，陈益峰，周创兵.考虑变形效应的非饱和土相对渗透系数模型[J].岩石力学与工程学报，2013，32（6）：1279-1287.（HU Ran，CHEN Yi-feng，ZHOU Chuang-bing.A relative hydraulic conductivity model for unsaturated deformable soils[J].Chinese Journal of Rock Mechanics and Engineering，2013，32 （6）：1279-1287.（in Chinese））

[2] 孙冬梅，朱岳明，张明进.降雨入渗过程的水-气二相流模型研究[J].水利学报，2007（2）：150-156.（SUN Dong-mei，ZHU Yue-ming，ZHANG Ming-jin.Water-air two-phase flow model for numerical analysis of rainfall infiltration[J].Hydraulic Engineering，2007 （2）：150-156.（in Chinese））

[3] 刘东燕，辜文杰，侯龙.降雨及地下水位对三峡库区非饱和土边坡稳定性的影响[J].水利水电技术，2013，44（7）：111-115.（LIU Dong-yan，GU Wen-jie，HOU Long.Rainfall and underground water level of Three Gorges Reservoir Area of unsaturated soil slope stability[J].Water Resources and Hydropower Engineering，2013，44 （7）：111-115.（in Chinese））

[4] Tong F，Niemi A，Yang Z，et al.A numerical model of tracer transport in a non-isothermal two-phase flow system for CO2 geological storage characterization[J].Transport in Porous Media，2013，98（1）：173-192.

[5] 袁俊平，褚飛飞，季李通.饱和—非饱和非稳定渗流数值分析中初始状态的研究[J].水利水电技术，2006（09）：5-7.（YUAN Jun-ping，ZHU Fei-fei，JI Li-tong.Study on initial condition in numerical analysis of saturated-unsaturated seepage flow[J].Technology of Water Conservancy and Hydroelectric Power，2006 （09）：5-7.（in Chinese））

[6] 朱伟，陈学东，钟小春.降雨入渗规律的实测与分析[J].岩土力学，2006，27（11）：1873-1879.（ZHU Wei，CHEN Xue-dong，ZHONG Xiao-chun.Observation and analysis of rainfall infiltration[J].Rock and Soil Mechanics，2006，27 （11）：1873-1879.（in Chinese））

[7] 肖蕾，骆世威.三峡库区某库岸边坡渗流及稳定性分析[J].水利水电技术，2014（2）：108-111.（XIAO Lei，LUO Shi-wei.Analysis on seepage and stability of a bank slope in Three Gorges Reservoir Area[J].Water Resources and Hydropower Engineering，2014 （2）：108-111.（in Chinese））

[8] Ali A，Huang J，Lyamin A V，et al.Boundary effects of rainfall-induced landslides[J].Computers and Geotechnics，2014，61：341-354.

[8] 高红贝，邵明安.温度对土壤水分运动基本参数的影响[J].水科学进展，2011，22（4）：484-494.（GAO Hong-bei，SHAO Ming-an.Effect of temperature on soil moisture parameters[J].Advances in Water Science，2011，22 （4）：484-494.（in Chinese））

[9] 陈益峰，周创兵，童富果，等.多相流传输THM全耦合数值模型及程序验证[J].岩石力学与工程学报，2009，28（4）：649-665.（CHEN Yi-feng，ZHOU Chuang-bing，TONG Fu-guo，et.A numerical model for fully coupled THM processes with multiphase flow and code validation[J].Chinese Journal of Rock Mechanics and Engineering，2009，28 （4）：649-665.（in Chinese））

[10] 陈玉超.冻融环境下岩土边坡稳定性研究初探[D].西安科技大学，2006.（CHEN Yu-chao.Preliminary study on rock and soil slope stability under the freezing-thawing condition[D].Xi′an University of Science and Technology，2006.（in Chinese））

[11] 张彬，刘宁，王红云.基于温度场对边坡降雨入渗的模拟分析[J].水资源与水工程学报，2011，22（6）：141-144.（ZHANG Bin，LIU Ning，WANG Hong-yun.Simulation analysis of landslide rainfall infiltration based on temperature field[J].Journal of Water Resources and Water Engineering，2011，22 （6）：141-144.（in Chinese））

[12] 张有天，刘中.降雨过程裂隙网络饱和-非饱和、非恒定渗流分析[J].岩石力学与工程学报，1997（2）：9-16.（ZHANG You-tian，LIU Zhong.Saturated/unsaturated，unsteady seepage analysis of rock fractured networks due to the percolation of rainfall[J].Chinese Journal of Rock Mechanics and Engineering，1997 （2）：9-16.（in Chinese））

[13] 吴志伟，宋汉周.基于Lu模型的浅部地温场与渗流场耦合研究[J].水利学报，2014.（WU Zhi-wei，SONG Han-zhou.Study on shallow geothermal field and seepage field coupling based on Lu Model[J].Journal of Hydraulic Engineering，2014.（in Chinese））

[14] 刘建强，黄金廷.饱和—非饱和带温度动态与气象因素关系[J].地下水，2013（02）：21-23.（LIU Jian-qiang，HUANG Jin-ting.Relation between temperature dynamic and meteorological factors in saturated-unsaturated zone[J].Groundwater，2013 （02）：21-23.（in Chinese））

[15] Tong F G，Jing L，Zimmerman R W.A fully coupled thermo-hydro-mechanical model for simulating multiphase flow，deformation and heat transfer in buffer material and rock masses[J].International Journal of Rock Mechanics and Mining Sciences，2010，47：205–217.

[16] 林鴻州，于玉贞，李广信，等.土水特征曲线在滑坡预测中的应用性探讨[J].岩石力学与工程学报，2009（12）：2569-2576.（LIN Hong-zhou，YU Yu-zhen，LI Guang-xin，et al.On application of soil-water characteristic curves to landslide forecast[J].Chinese Journal of Rock Mechanics and Engineering，2009 （12）：2569-2576.（in Chinese））

[17] Van Genuchten M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal，1980，44：892-898.

[18] Mualem Y.A new model for predicting the hydraulic conductivity of unsaturated porous media[J].Water Resources Research，1976，12：513-522.

[19] 蔡国庆，赵成刚，刘艳.一种预测不同温度下非饱和土相对渗透系数的间接方法[J].岩土力学，2011，32（5）：1405-1410.（CAI Guo-qing，ZHAO Cheng-gang，LIU Yan.An indirect method for predicting permeability coefficients of unsaturated soils at different temperatures[J].Rock and Soil Mechanics，2011，32 （5）：1405-1410.（in Chinese））

[20] Corey A T.The interrelation between gas and oil relative permeabilities[J].Producers Monthly，1954，19：38-41.

[21] Guvanasen V，Chan T.A three-dimensional numerical model for thermos hydro mechanical deformation with hysteresis in a fractured rock mass[J].International Journal of Rock Mechanics and Mining Sciences，2000，37：89-106.

[22] Pritchett J W，Rice M H，Riney T D.Equation of state for water-carbon dioxide mixtures：implications for Baca reservoir[J].Report DOE/ET/27163-8，UC-66a，La Jolla，CA （1981）

[23] Tong F G，Jing L，Zimmerman R W.A fully-coupled finite element code for modeling thermo-hydro-mechanical processes in porous geological media.In：Proceedings 43rd US Rock Mechanics Symposium，28-30 June 2009 Asheville，NC，USA，Smeallie P，ed.Document ID：09-120.

[24] 孔祥言編著.高等渗流力学[M].合肥：中国科学技术大学出版社，1999.（KONG Xiang-yan.Seepage mechanics[M].Hefei：University of Science & Technology China Press，1999.（in Chinese））

[25] 陈伟，莫海鸿，陈乐求.非饱和土边坡降雨入渗过程及最大入渗深度研究[J].矿冶工程，2009，29（6）：13-16，21.（CHEN Wei，MO Hai-hong，CHEN Yue-qiu.Study on rainfall infiltration process and the biggest infiltration depth for unsaturated soil slope[J].Mining and Metallurgical Engineering，2009，29 （6）：13-16，21.（in Chinese））

[26] 张士宇，王瑞钢.降雨对高填土路堤的入渗深度的确定及有限元稳定分析[J].路基工程，2004（5）：17-21.（ZHANG Shi-yu，WANG Rui-gang.Calculation of depth for rainfall infiltration into subgrades and stability analysis with finite methods[J].Subgrade Engineering，2004 （5）：17-21.（in Chinese））