落水洞水位对水文情景响应变化的试验研究

张春艳 束龙仓 程艳红 张帅领

摘 要：岩溶含水系统水流运动规律的研究对岩溶地区水资源可持续利用和经济发展具有重要意义。物理模型一定程度上可以随意设置不同的试验条件及水文情景，是研究岩溶水流运动规律的有效工具之一。利用自行设计研制的裂隙网络-管道双重介质物理模型，设置3种不同的补排关系、6个不同的泉口直径、3个不同的含水层倾角，研究落水洞水位变化规律。结果表明：补给大于排泄、含水层无倾角时，落水洞水位呈对数曲线趋势上升;补给大于排泄、含水层有倾角时，落水洞水位变化可用二次函数描述;补给小于排泄、含水层无倾角时，落水洞水位呈阶梯状下降，且阶梯个数与层面裂隙条数相等;补给小于排泄、含水层有倾角时，落水洞水位呈直线下降。同一泉口直径，无论含水层有无倾角，落水洞水位下降可由同斜率、不同截距的直线簇表达。

关键词：落水洞水位;裂隙网络;管道;双重介质;水文情景

中图分类号：P641.73文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.06.010

Experimental Study on the Responses of Groundwater Level Changes in the

Sinkhole on Different Hydrology Scenarios

ZHANG Chunyan1， SHU Longcang2， CHENG Yanhong3， ZHANG Shuailing4

（1.College of Geosciences and Engineering， North China University of Water Resources and Electric Power， Zhengzhou 450046， China;

2.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering， Hohai University， Nanjing 210098， China;

3.State Grid Henan Electric Power Company， Zhengzhou 450052， China;

4.Central China Electric Power Engineering Corporation Limited， Zhengzhou 450007， China）

Abstract：The study on the groundwater flow is essential to the sustainable development of water resources and economy in the karst areas. The physical model is an effective way to investigate the changes of karst groundwater flow because it can be changed according to the experiments conditions and hydrological scenarios. A physical model of fractures network-conduits was built. Three different hydrological scenarios， six different diameters of discharge outlet and three different angels of the aquifer layer were set to investigate the response of groundwater level to these different conditions. The results show that the groundwater level in the sinkhole increased as log curve when the recharge is more than discharge and the aquifer is horizontal， while it is quadratic curve when the aquifer is not horizontal. The groundwater level is decreased as steps line when the recharge is less than the discharge and the aquifer is horizontal under different diameters of the spring outlets， while it decreases as straight line when the aquifer is not horizontal. The groundwater level can be depicted as a group of straight lines under the condition of the same spring outlet diameter whether the aquifer has an angel or not.

Key words： groundwater level in sinkhole; fractures network; conduits; dual-media; hydrological scenarios

岩溶含水系統通常具有孔隙的多重性、入渗过程的多重性以及排泄过程的多重性[1]，从而导致岩溶含水系统的高度非均质性，因此传统的地下水流运动规律（如达西定律）在岩溶含水系统中不再适用，野外试验等传统的水文地质学方法在岩溶含水系统中也难以应用[2-3]。在孔隙介质中通过地下水位观测井，可以准确地连续观测到地下水位变化，然而相同的方法在岩溶含水系统中不再适用，近距离分布的观测井可能得到随机分布的不同观测数据，但差值可能达到几米甚至十几米，更有甚者，打在岩石中的观测井则无法观测到水流运动，无法达到试验目的[4-5]。因此，通过物理模型试验研究岩溶含水系统水流运动规律十分必要。Faulkner等[6]、Gallegos等[7]建立了岩溶孔隙-管道双重介质物理模型，模拟了渗流和管流的耦合情况，进行了水流和溶质运移试验。Qian等[8]建立了室内充填裂隙物理模型，进行了水流和溶质运移试验，研究了充填裂隙中非达西流和非费克溶质运移现象。陈冰宇[9]建立了上层孔隙介质、下层裂隙介质的双重介质物理模型，进行了水流和溶质运移试验。李琛亮等[10]利用自行设计研制的孔隙-裂隙双重介质渗流水力特性试验系统，研究了水量交换、渗流场的水压分布规律以及双重介质的水力性质和渗流机制。腾强等[11]基于离散裂隙网络模型和裂隙介质管道流模型，建立了一套室内裂隙介质管道网络试验装置，并开展了裂隙渗流试验，指出流量与有效孔隙率及裂隙密度、溶质通量与流量及裂隙密度之间皆存在较好的统计关系。宋静文等[12]利用相互正交的裂隙网络物理模型，研究了裂隙网络结构与几何参数对溶质运移的控制作用。孙晨等[13]、束龙仓等[14]、Tang等[15]、牛子豪等[16]利用室内裂隙网络-管道双重介质物理模型，进行了泉流量对补给方式、含水层倾角的响应试验，通过示踪试验探究了裂隙-管道介质间不同补给方式下水流交换情况。刘波等[17]利用与腾强等[11]相同的试验装置探求了不同裂隙几何参数对裂隙网络溶质运移的影响。赵小二等[18]基于室内水箱-管道系统，研究了岩溶管道中溶潭对溶质运移的影响。从文献中可以看出，众多学者利用物理模型研究渗流-管流耦合、泉流量衰减规律以及溶质运移规律等，而落水洞作为岩溶含水系统重要的组成部分，是地表水流入地下的进口，是地表与地下岩溶地貌的过渡，其水位变化影响到地表径流的再分配。落水洞水位的变化与地下水的补排关系密切相关，含水层补给与排泄关系的研究方法主要有室内物理模型[6， 19]、经验模型[20-21]、水库模型[22-23]、统计模型[24-25]和信号理论[26-27]等。本文主要通过室内物理模型试验研究落水洞水位对于不同水文情景（补排关系）以及不同含水层结构特征（含水层倾角、泉口直径）的响应变化。

1 物理模型装置

图1为贵州后寨河流域野外地层的露天照片。该流域含水介质主要包括层面裂隙和垂直层面裂隙。根据前人对后寨河流域的调查研究[28-30]，将其概化为图2所示的岩溶含水系统概念模型。从图2中可以看出，后寨岩溶系统包括层面裂隙、垂直层面裂隙、管道和落水洞等。

以后寨岩溶含水系统为原型，进行概化处理，得到室内裂隙网络-管道双重介质物理模型。室内物理试验系统包括裂隙网络-管道双重介质模型、供水装置、水头监测系统以及泉流量测量装置（见图3）。

裂隙网络-管道双重介质物理模型由两块平行光滑透明的有机玻璃板组成，可直观观测到内部水流运动过程。在其中一块透明有机玻璃板上，固定有96块尺寸为10 cm×10 cm×3 cm、8块尺寸为10 cm×5 cm×3 cm相间排列的透明玻璃砖，相邻两行玻璃砖之间的空隙构成层面裂隙，开度均值为0.5 cm，共7条。相邻两列玻璃砖之间的空隙构成垂直层面裂隙，开度均值为0.12 cm，每层12条，共96条。层面裂隙与垂直层面裂隙构成了裂隙网络，裂隙网络区尺寸为126.5 cm×86.5 cm×3.0 cm。玻璃砖与另一块玻璃板之间铺有一块薄橡胶皮，橡胶皮与玻璃砖之间用透明胶粘合，以防止水流在裂隙和管道之外的空隙流动。两块平行玻璃板的外侧用三组钢条固定，防止试验过程中水压过大使装置变形。底部管道由模型底部预留的空隙构成，尺寸为129.5 cm×3.0 cm×3.0 cm。落水洞由模型右侧预留的空隙构成，尺寸为3.0 cm×86.5 cm×3.0 cm。装置顶部为分散补给区，用以模拟降雨补给系统。装置顶端及两侧装有排气管，在降雨补给过程中可排出装置中的空气，避免空气滞留在装置中造成水流不饱和而影响试验结果。

水头监测系统主要包括水头测量装置（27只压力传感器）、信号转换装置（巡检仪）和信号输出装置（一台电脑）。27只压力传感器分布于裂隙网络-管道模拟区（见图3）。压力传感器型号为HM20-1-A1-F2-W2，测量范围为0～100 kPa，精度为0.1 cm水柱。压力传感器输出的电信号通过巡检仪装置转换为数字信号，最后通过电脑以Excel表格形式输出，输出的时间序列间隔最小为1 s。

供水装置可以提供定水头和变水头试验条件，定水头试验条件由供水箱一侧的溢流管实现，降雨强度的大小可通过调节阀门开启度进行调节。

2 试验条件设置

（1）水文情景设置。设置3种不同的水文情景研究落水洞水位变化特征：①水文情景一（S1），设置为只有补给没有排泄，模拟丰水期强降雨条件下补给远大于排泄，研究落水洞水位对补给强度的响应变化;②水文情景二（S2），设置为只有排泄没有补给，模拟枯水期补给可以忽略不计，研究落水洞水位对排泄强度的响应变化;③水文情景三（S3），设置为既有补给又有排泄，模拟平水期地下水的补给与排泄同时存在。

水文情景一（S1）中，排泄口阀门保持关闭，设置不同的补给强度。试验开始前，设置定水头补给，然后打开补给阀门，进行恒定补给强度补给，直至装置中水位上升至介质顶部，试验结束。水文情景二（S2）中，设置不同的含水层初始饱和厚度。对应每一个含水层初始饱和厚度，用不同直径的塑胶管连接装置底部管道出口，模拟不同直径的泉口，以此来设置不同的泉口直径。试验开始前，关闭排泄口阀门，打开补给阀门，开始补给裂隙网络-管道含水介质，直至水位升至某一高度（此高度即为含水层初始饱和厚度）后，关闭补给阀门。打开排泄阀门，试验开始，水从泉口流出，流入排泄水箱，直至水流从装置中全部排出，试验结束。水文情景三（S3）中，同时打开补给阀门和排泄阀门，若试验开始时补给大于排泄，则裂隙网络-管道模型中水位上升，水位上升至装置顶部时，关闭补给阀门，直至水流从装置中排完，试验结束。若试验开始时补给等于排泄，则至裂隙网络-管道模型中水位达到平衡时关闭补给阀门，直至水流从装置中排完，试验结束。

（2）泉口直径（d）設置。岩溶水中的侵蚀性二氧化碳会对岩石产生侵蚀作用，从而产生溶孔、溶洞，或使溶洞规模扩大。由于泉口与岩溶水的作用时间最长、侵蚀作用最强，因此在研究中主要考虑泉口直径的变化。泉口直径的设置，可通过在排泄口处连接不同直径的塑胶管实现。

（3） 含水层倾角（α）设置。在试验装置的落水洞一侧垫入不同高度的玻璃砖块来改变含水层倾角，倾角分别设置为0°、5°、8° 。

3 试验结果及分析

3.1 落水洞水位对水文情景一（S1）的响应

（1）含水层倾角α=0°。8个不同补给强度（Qre）下，落水洞水位随时间变化见图4。

分别对8条水位变化曲线进行拟合，得到落水洞水位与时间之间的函数关系式：

H=Aln t+B（1）

式中：H为落水洞水位，cm;t为时间，s;A、B为系数。

系数A与补给强度Qre之间存在线性关系，如图5所示。

常数项B与补给强度Qre之间无明显函数关系，B值在-346.71至-293.72之间变化，取其平均值-317.67，记为B0。可得落水洞水位变化表达式：

H=f（Qre）ln t+B0（2）

（2）含水层倾角α=5°。9个不同补给强度（Qre）条件下，落水洞水位随时间变化见图6。

对9条曲线进行拟合，得到落水洞水位与时间之间的函数关系：

H=p1t2+p2t+p3（3）

式中：p1、p2、p3为系数，与补给强度Qre存在函数关系。

经相关分析得：

p1=-2.143×10-6Q2re+1.036×10-5Qre+

3.823×10-5 （R2=0.924 9）

p2=0.039 6Qre-0.017 9 （R2=0.861 7）

p3=-1.483Qre-20.760 （R2=0.928 0）

（3）含水层倾角α=8°。9个不同的补给强度（Qre）条件下，落水洞水位随时间变化见图7。

对9条曲线进行拟合，得到落水洞水位与时间之间的函数关系：

H=p4t2+p5t+p6（4）

式中：p4、p5、p6为系数，与补给强度Qre存在函数关系。

经相关分析得：

p4 =-4.251×10-6Q2re+3.609×

10-5Qre -1.177×10-4  （R2=0.998 8）

p5=0.046 1Qre -0.066 1  （R2=0.990 5）

p6=-1.132 6Qre -15.916  （R2=0.997 5）

（4）对比分析。3组试验结果相同点：无论含水层有无倾角，补给强度越大，含水层底部管道开始得到补给的时刻越早，落水洞水位上升开始的时间就越早，即水流滞后时间越短，落水洞水位上升越快;在同一补给强度条件下，随落水洞水位不断上升，上升变化率减小，原因主要是水流在裂隙网络中的滞后导致补给到裂隙网络-管道含水介质中的水流不能直接到达底部管道和落水洞，而是经过裂隙网络的“过滤”，相对于管道而言，由于裂隙网络的弱渗透性，在含水层得到补给后，并非全部的水流直接到达底部管道和落水洞，而在补给过程中始终有一部分水储存在裂隙网络中，随着水位上升，下部的裂隙网络-管道介质逐渐饱和，非饱和含水层部分的体积越来越小，从而使非饱和区储存水量对于饱和区的补给量越来越少，因此导致水位上升变化率逐渐减小。3组试验结果不同点：①含水层无倾角时，不同补给强度条件下，落水洞水位与时间之间成对数函数关系;含水层有倾角时，不同补给强度条件下，落水洞水位与时间之间成二次多项式函数关系。②含水层无倾角时落水洞水位的变化曲线比较粗糙，有倾角时落水洞水位变化曲线比较光滑，产生这一差异的原因是层面裂隙的过渡作用，含水层无倾角时层面裂隙的过渡作用比较强，有倾角时水流流速增大使层面裂隙的过渡作用减弱。

3.2 落水洞水位对水文情景二（S2）的响应

（1）含水层倾角α=0°。不同泉口直径条件下，落水洞水位对含水层初始饱和厚度M的响应变化见图8（以d=3 mm和d=5 mm为例）。

初始饱和厚度的响应变化（S2，α=0°）

对于同一个泉口，不同含水层初始饱和厚度条件下，落水洞水位下降曲线斜率基本相同，由直线概化，可得：

H=C0t+M（5）

式中：M为含水层初始饱和厚度，cm;C0为系数（下角标对应含水层倾角），其值与泉口直径d存在函数关系C0=-0.310 3d+0.938 5（R2=0.984）。

（2）含水层倾角α=5°。不同泉口直径条件下，落水洞水位对含水层初始饱和厚度的响应变化见图9（以d=4 mm和d=6 mm为例）。

初始饱和厚度的响应变化（S2，α=5°）

不同泉口直径条件下，落水洞水位随时间均呈直线变化。同一泉口时，为一簇同斜率、不同截距的直线：

H=C5t+M（6）

其中：

C5= -0.319 7d+1.050 9  （R2 = 0.990 7）

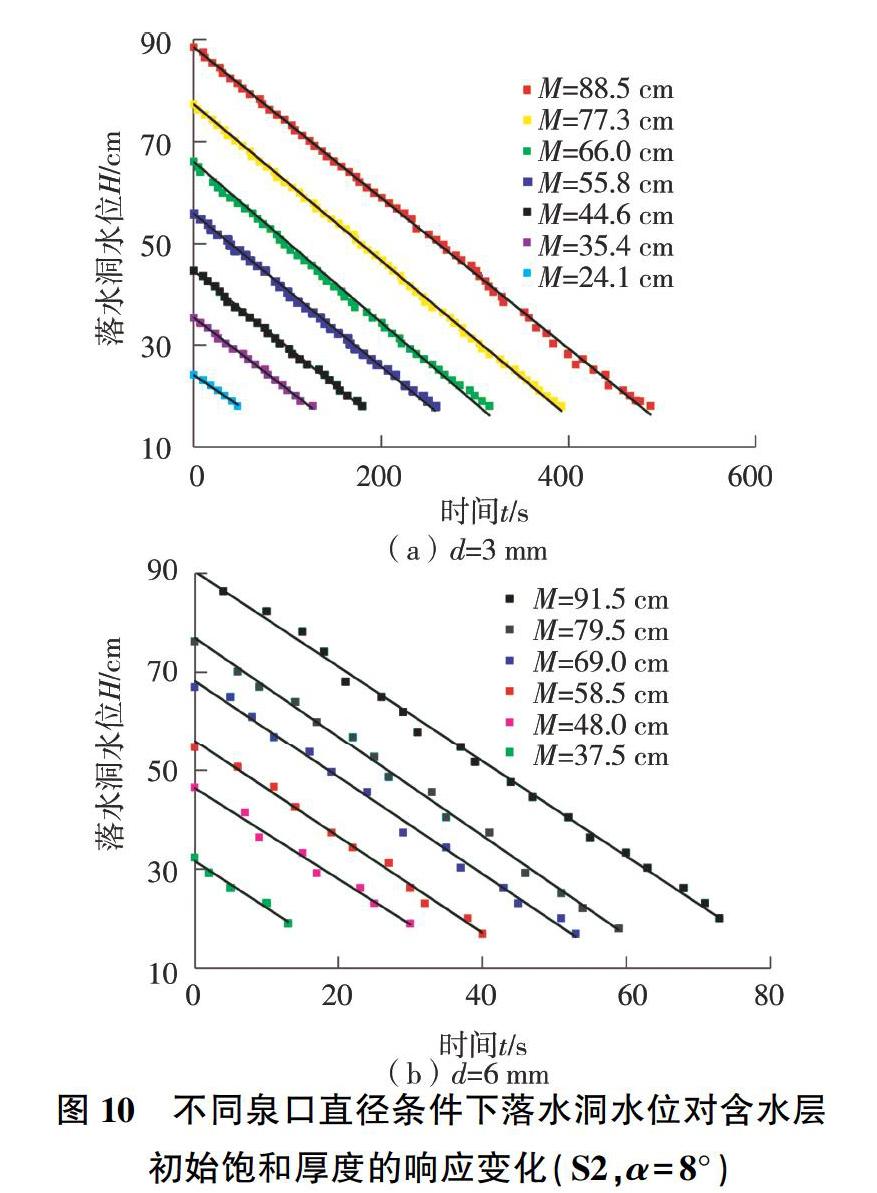
（3）含水层倾角α=8°。不同泉口直径条件下，落水洞水位对含水层初始饱和厚度的响应变化见图10（以d=3 mm和d=6 mm为例）。

初始饱和厚度的响应变化（S2，α=8°）

落水洞水位变化规律同α= 5°，经相关分析可得，落水洞水位变化方程为

H=C8t+M（7）

其中：

C8= -0.398 7d+1.274 7  （R2 = 0.939 4）

（4）對比分析。3组试验结果相同点：无论含水层有无倾角，含水层初始饱和厚度对落水洞水位变化影响较小。落水洞水位随时间变化曲线可由一簇相同斜率、不同截距（即含水层初始饱和厚度）的直线H=Cαt+M描述，系数Cα与泉口直径d之间呈线性关系，泉口越大，水位下降速率越大;泉口较小时落水洞水位变化受含水层倾角影响较小，泉口越大水位变化受含水层倾角影响越大，原因是泉口较小时，落水洞水位变化主要受泉口直径的限制，而受含水层倾角影响较弱。3组试验结果不同点：①含水层无倾角时，落水洞水位随时间呈阶梯状下降（d为3、4、5 cm时），随着泉口增大，阶梯状越来越不明显，甚至消失（d为6、8、10 cm时）;水位下降呈阶梯状主要受层面裂隙影响，流入垂向裂隙的水，汇集至层面裂隙，相比垂向裂隙水流，层面裂隙水流流速减小，而且有一部分水流入落水洞，经过层面裂隙的过渡，使得落水洞水位间断性下降变缓，即表现为图8中的阶梯状，而且图8中阶梯个数（7个）与层面裂隙条数（7条）一致，也验证了以上解释，这一过程在试验过程中也可以观测到;随着泉口增大（d为6、8、10 cm时），水位下降的阶梯状越来越不明显，甚至消失，原因是泉口增大，水流流速增大，水位下降速率增大，弱化了层面裂隙的过渡作用。②含水层有倾角时，落水洞水位随时间呈直线下降，相比水平含水层，层面裂隙中的水流流速增大，弱化了层面裂隙的过渡作用，从而使得水位下降呈直线。

3.3 落水洞水位对水文情景三（S3）的响应变化

d=3 mm、α=0°时，落水洞水位随时间变化见图11（a）;d=3 mm、α=8°时，落水洞水位随时间变化见图11（b）。

水文情景三是水文情景一与水文情景二的结合，因此含水层倾角为0°时，落水洞水位变化数学模型为

H=f（Qre-Qdis）ln t+B0 （t≤T）

C0t+M （t>T）（8）

式中：Qdis為排泄强度，mL/s;T为补给历时，s。

含水层有倾角（5°、8°）时，落水洞水位变化数学模型为

H=pit2+pjt+pk  （t≤T）

Cαt+M （t>T）（9）

式中：pi，pj，pk为系数;Cα为含水层倾角为α时对应的系数C。

应用含水层倾角为0°对应的数学模型对补给强度为26.19 mL/s时的落水洞水位预测模型进行验证，结果如图12（a）所示，均方根误差（RMSE）为0.661，确定系数（R2）为0.995。应用含水层倾角为8°对应的数学模型对补给强度为26.12 mL/s时的落水洞水位预测模型进行验证，结果如图12（b）所示，均方根误差（RMSE）为0.668，确定系数（R2）为0.996。

4 结 论

利用裂隙网络-管道双重介质物理模型进行不同水文情景及模型结构条件下，落水洞水位变化规律的试验研究，得到以下结论。

（1）补给大于排泄、含水层无倾角时，落水洞水位随时间呈对数函数上升，变化曲线比较粗糙;含水层有倾角时，落水洞水位随时间呈二次函数上升，变化曲线较光滑。含水层倾角越大，落水洞水位上升越慢，且裂隙网络的“过滤”作用使落水洞水位上升变化率随时间减小。

（2）补给小于排泄、含水层无倾角时，落水洞水位随时间呈阶梯状下降，且阶梯个数与层面裂隙条数一致，原因是层面裂隙中水流速度较垂直裂隙中水流流速小。含水层有倾角时，落水洞水位随时间呈直线下降，倾角越大，水位下降越快。

本文建立了落水洞水位与补排强度、泉口直径、含水层初始饱和厚度以及时间的数学模型，可以为落水洞水位变化预测，判断含水层有无倾角、层面裂隙条数等提供参考。

参考文献：

[1] WHITE W B. Geomorphology and Hydrology of Karst Terrains[M]. New York：Oxford University Press， 1988：464.

[2] CIVITA M V. An Improved Method for Delineating Source Protection Zones for Karst Springs based on Analysis of Recession Curve Data[J]. Hydrogeology Journal，2008，16（5）：855-869.

[3] FORD D C， EWERS R O. The Development of Limestone Cave Systems in the Dimensions of Length and Depth[J]. Canadian Journal of Earth Sciences，2011，15（15）：1783-1798.

[4] GHASEMIZADEH R， HELLWEGER F， BUTSCHER C， et al. Review： Groundwater Flow and Transport Modeling of Karst Aquifers， with Particular Reference to the North Coast Limestone Aquifer System of Puerto Rico.[J]. Hydrogeology Journal，2012，20（8）：1441-1461.

[5] KONG-A-SIOU L， CROS K， JOHANNETA， et al. Knox Method， or Knowledge Extraction from Neural Network Model. Case Study on the Lez Karst Aquifer （Southern France）[J]. Journal of Hydrology，2013，507（18）：19-32.

[6] FAULKNER J， HU B X， KISH S， et al. Laboratory Analog and Numerical Study of Groundwater Flow and Solute Transport in a Karst Aquifer with Conduit and Matrix Domains.[J]. Journal of Contaminant Hydrology，2009，110（1-2）：34.

[7] GALLEGOS J J， HU B X， DAVIS H. Erratum： Simulating Flow in Karst Aquifers at Laboratory and Sub-Regional Scales Using MODFLOW-CFP[J]. Hydrogeology Journal，2013，21（8）：1911-1912.

[8] QIAN J Z， CHEN Z， ZHAN H B， et al. Solute Transport in a Filled Single Fracture under non-Darcian Flow[J]. International Journal of Rock Mechanics & Mining Sciences， 2011，48（1）：132-140.

[9] 陈冰宇. 不同水流、几何及基质属性条件下裂隙水运移试验研究[D]. 合肥：合肥工业大学，2013：88-95.

[10] 李琛亮，沈振中，赵坚，等. 双重介质渗流水力特性试验装置研究及应用[J]. 巖土力学，2013，34（8）：2421-2429.

[11] 腾强，王明玉，王慧芳. 裂隙管道网络物理模型水流与溶质运移模拟试验[J]. 中国科学院大学学报，2014，31（1）：54-60.

[12] 宋静文，王明玉，汤大伟. 基岩裂隙水三维渗流网络溶质运移试验研究[J]. 给水排水，2014，40（增刊1）：50-53.

[13] 孙晨，束龙仓，鲁程鹏，等. 裂隙-管道介质泉流量衰减过程试验研究及数值模拟[J]. 水利学报，2014，45（1）：50-57.

[14] 束龙仓，范建辉，鲁程鹏，等. 裂隙-管道介质泉流域水文地质模拟试验[J]. 吉林大学学报（地球科学版），2015，45（3）：908-917.

[15] TANG R， SHU L， LU C， et al. Laboratory Analog Analysis of Spring Recession Curve in a Karst Aquifer with Fracture and Conduit Domains[J]. Journal of Hydrologic Engineering，2016，21（2）：06015013.

[16] 牛子豪，束龙仓，林欢，等. 不同补给条件下裂隙-管道介质间水流交换的示踪试验研究[J]. 水文地质工程地质，2017，44（3）：6-11.

[17] 刘波，王明玉，张敏，等. 裂隙网络管道模型弥散试验[J]. 吉林大学学报（地球科学版），2016，46（1）：230-239.

[18] 赵小二，常勇，彭伏，等. 水箱-管道系统溶质运移实验研究及其岩溶水文地质意义[J]. 吉林大学学报（地球科学版），2017，47（4）：1219-1228.

[19] CRISS R E， WINSTON W E. Hydrograph for Small Basins Following Intense Storms[J]. Geophysical Research Letters，2003，30（6）：41-47.

[20] JUKI D， DENI-JUKI V. Groundwater Balance Estimation in Karst by Using a Conceptual Rainfall-Runoff Model[J]. Journal of Hydrology，2009，373（3）：302-315.

[21] LIU L， SHU L， CHEN X， et al. Rainfall-Driven Spring Hydrograph Modeling in a Karstic Water System， Southwestern China[J]. Water Resources Management，2010，24（11）： 2689-2701.

[22] KURTULUS B， RAZACK M. Evaluation of the Ability of an Artificial Neural Network Model to Simulate the Input-Output Responses of a Large Karstic Aquifer： the La Rochefoucauld Aquifer （Charente， France）[J]. Hydrogeology Journal，2007，15（2）：241-254.

[23] TRITZ S， GUINOT V， JOURDE H. Modelling the Behaviour of a Karst System Catchment Using Non-Linear Hysteretic Conceptual Model[J]. Journal of Hydrology，2011，397（3）：250-262.

[24] PADILLA A， PULIDO-BOSCH A. Study of Hydrographs of Karstic Aquifers by Means of Correlation and Cross-Spectral Analysis[J]. Journal of Hydrology，1995，168（1-4）：73-89.

[25] SIOU L K A， JOHANNET A， BORRELL V， et al. Erratum to “Complexity Selection of a Neural Network Model for Karst Flood Forecasting： the Case of the Lez Basin （Southern France）” [J]. Journal of Hydrology，2011，406（1）：136.

[26] LABAT D， ABABOU R， MANGIN A. Rainfall-Runoff Relations for Karstic Springs. Part Ⅱ： Continuous Wavelet and Discrete Orthogonal Multiresolution Analyses[J]. Journal of Hydrology，2000，238（3-4）：149-178.

[27] JRR C E， RANA A J， POULTON M M， et al. A Neural Network Model for Predicting Aquifer Water Level Elevations[J]. Groundwater，2005，43（2）：231-241.

[28] 杨剑明，张兆干.贵州普定后寨地下河流域地下含水空间结构特征[J].中国岩溶，1996，15（3）：246-252.

[29] 张兆干，杨剑明.喀斯特地块空间结构研究：以普定后寨地下河流域为例[J].地理学报，1997，46（4）：345-352.

[30] 王腊春，许有鹏，张立峰，等.贵州普定后寨地下河流域岩溶水特征研究[J].地理科学，2000，20（6）：557-562.

【责任编辑 张华兴】