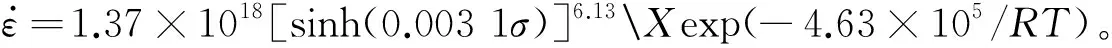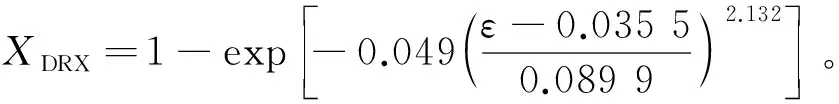GH4169镍基高温合金的热变形行为与再结晶模型

王 稳

(1.苏州健雄职业技术学院中德工程学院，太仓 215411；2.江苏大学材料科学与工程学院，镇江 212013)

0 引 言

GH4169(NiCr19Fe19Nb5)高温合金是以γ相为基体，γ′和γ″相为强化相的变形高温合金[1]，在高温服役条件下具有较高的屈服强度,优良的抗氧化性能、抗疲劳性能和耐腐蚀性能[2-5]，广泛应用于石油工业、航空航天、核电等领域[6-7]。近年来，航空发动机对发动机叶片、涡轮盘等关键零部件的制造精度、服役性能的要求越来越严苛，这对材料的性能提出了更高的要求。镍基变形高温合金较难利用热处理的方法强化性能，而通过控制热变形工艺可以调控显微组织，提高性能[8]。

在热变形过程中，合金的动态再结晶是一种重要的组织演化行为。动态再结晶可软化应变硬化合金，提高合金的塑性和延展性，改善合金的塑性加工性能[9]；动态再结晶也是合金细化晶粒，控制显微组织的关键技术[10]。动态再结晶行为的研究是合金高温变形行为研究的重要内容。Avrami动力学模型作为研究动态再结晶的重要方法，已在多种合金的动态再结晶行为研究中得到较多应用[11]。MIRZADEH等[12]利用Avrami模型成功预测了17-4PH不锈钢发生动态再结晶的临界条件；ZHANG等[13]建立了GH4742合金的再结晶模型；CHEN等[14]建立了3003铝合金的再结晶体积分数模型。众多研究表明，Avrami再结晶模型可较准确地描述各类合金的动态再结晶行为。

作者采用Gleeble-3500型热力模拟试验机对GH4169高温合金进行了热压缩试验，研究了合金热压缩变形行为及变形后的显微组织，基于流变数据建立了Arrhenius双曲正弦高温本构方程，并利用Avrami方程构建GH4169高温合金的动态再结晶模型，拟为材料热加工工艺的制定提供理论指导。

1 试样制备与试验方法

试验材料为GH4169高温合金，由江苏银环精密钢管有限公司提供，化学成分如表1所示。在试验合金上加工出尺寸为φ8 mm×12 mm的圆棒状试样，利用Gleeble-3500型热力模拟试验机进行等温恒应变速率热压缩试验。试样以10 ℃·s-1的速率升温至1 100 ℃保温600 s后，以5 ℃·s-1的速率降至热变形温度(9001 100 ℃)，保温30 s后进行应变速率为0.015 s-1的热压缩变形，压缩至真应变为0.8。试验环境为真空，通过K型热电偶丝测定试样温度，在试样与压头的接触面上放置一层0.05 mm厚的钽片，以减小试样与压头的摩擦，防止试样与压头粘连。热压缩后，利用高速氩气气流，对试样进行气淬，以保留高温变形组织。采用线切割将热压缩试样沿轴线剖开，剖面磨抛后，采用由12 mol·L-1盐酸，20 mL无水乙醇，1.5 g硫酸铜配制而成的腐蚀液进行腐蚀，腐蚀时间13 min，采用Lecia DMI8C型光学显微镜观察显微组织。

表1 GH4169高温合金的化学成分(质量分数)Table 1 Chemical composition of GH4169 superalloy (mass) %

2 试验结果与讨论

2.1 显微组织

由图1可以看出：在950 ℃，1 s-1条件下压缩至真应变为0.8后，试验合金形成典型的不完全动态再结晶“项链”组织[15]，这是由于较低变形温度下的再结晶形核速率较慢，同时较高的应变速率抑制再结晶，且再结晶晶粒主要分布在原始变形晶界上，晶粒内部的再结晶晶粒较少，从而呈现“项链”特征；当应变速率降至0.01 s-1时，晶界迁移时间变得充分，试验合金发生完全动态再结晶，形成完全动态再结晶组织，且由于试验温度较低，晶界迁移速度较慢，故再结晶晶粒长大不明显。当变形温度升高到1 100 ℃时，热激活作用增强，试验合金发生完全动态再结晶(再结晶晶粒占据视野的95%以上即可认为发生完全动态再结晶)，高应变速率(1 s-1)下，仍存在极少量的原始组织；低应变速率(0.01 s-1)下的再结晶晶粒尺寸更大，说明低应变速率下的再结晶晶粒发生了长大。综上所述，GH4169高温合金在高温、低应变速率条件下更容易发生再结晶。

图1 不同条件下热压缩变形至应变为0.8后GH4169高温合金的显微组织Fig.1 Microstructure of GH4169 superalloy after hot compression deformation to a strain of 0.8 under different conditions

2.2 真应力-应变曲线

在相同变形温度下，当应变速率较高时，试验合金的再结晶孕育时间较短，再结晶体积分数较低，再结晶软化效果不明显，因此变形抗力处于较高水平，如图2(a)所示；在相同应变速率下，当变形温度较高时，合金的热激活作用加强，动态再结晶形核率增加，软化效果明显，如图2(b)所示。在热变形初期，试验合金内部的位错迅速增殖、缠结，使得真应力快速上升，加工硬化率较大[16]。随着变形的继续，加工硬化率减小，真应力增速减缓，试验合金开始出现软化行为，真应力在达到峰值后随着应变的增加而下降，软化效果与加工硬化效果相互抵消，材料流变应力不再发生大幅变化。

图2 GH4169高温合金在不同热压缩变形条件下的真应力-应变曲线Fig.2 True stress-strain curves of GH4169 superalloy under different hot compression deformation conditions

2.3 本构方程

(1)

(2)

全应力水平

(3)

式中:Q为热变形激活能，kJ·mol-1；R为理想气体常数，8.314 J·mol-1·K-1；A1,A2,A，α，n，β，n1为材料常数，其中α=β/n1。

式(1)、式(2)和式(3)两侧取自然对数得到：

(4)

(5)

(6)

用式(4)式(6)对真应变为0.2时的流变数据进行线性拟合，如图3所示，得到α=0.003 1，n=6.13，A=1.37×1018，Q=4.63×105J·mol-1。因此，GH4169高温合金的本构方程为

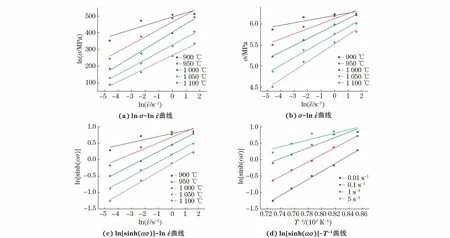
图3 GH4169高温合金本构模型中各参数的关系曲线Fig.3 Curves of various parameters in constitutive model of GH4169 superalloy: (a) curves;(c) curves and (d) ln[sinh(a σ)]-T-1 curves

exp(-4.63×105/RT)

(7)

2.4 临界动态再结晶模型

动态再结晶行为对材料显微组织和力学性能的影响很大[18]。动态再结晶的临界值是制定热加工工艺的重要参考，临界值的确定尤为重要。POLIAK等[19]和JONAS等[20]基于热力学不可逆原理，在加工硬化率θ的基础上建立了动态再结晶临界模型，认为材料发生动态再结晶的临界应变与加工硬化率-应变曲线上的拐点有关。试验合金的加工硬化率-应变曲线见图4(a)，图中难以明确拐点信息，故对加工硬化率取对数运算以提高准确性[21]。采用三次多项式对加工硬化率的自然对数和应变进行拟合，拟合公式为

lnθ=Aε3+Bε2+Cε+D

(8)

式中：A，B，C，D均为拟合系数。

对应变求导可得：

d(lnθ)/dε=3Aε2+2Bε+C

(9)

则试验合金的[d(lnθ)/dε]-e曲线见图4(b)，曲线拐点对应的横坐标即再结晶临界应变ec,即

图4 GH4169高温合金的加工硬化率和真应变以及不同变形条件下的εc-εp和σc-σp的关系曲线Fig.4 Curves of work hardening rate vs true strain (a-b) and curves of εc-εp (c) and σc-σp (d) under different deformation conditions of GH4169 superalloy

εc=-B/3A

(10)

按照上述步骤，得到不同变形温度(9001 100 ℃)

和应变速率(0.015 s-1)下的动态再结晶临界应变，再由应力-应变曲线确定对应的临界应力σc，以及峰值应力σp和峰值应变εp。由图4(c)和图4(d)可知，临界应变和峰值应变、临界应力和峰值应力之间均存在一定的线性关系，经拟合得到的线性方程如下：

εc=0.44εp-0.006

(11)

σc=0.79σp

(12)

由式(11)可知，当εc/εp约为0.44时，达到动态再结晶临界条件，试验合金发生动态再结晶。εc/εp越小，GH4169高温合金在热激活过程中的再结晶晶粒越容易形核[22]。由图4(d)可以看出，峰值应力和临界应力之间存在良好的线性相关性。

以1 100 ℃，0.01 s-1条件下的试样为例，采用Avrami动力学模型[23]对动态再结晶过程进行预测。其表达式如下：

XDRX=1-exp[-k[(ε-εc)/εp)]m]

(13)

式中：XDRX为动态再结晶体积分数，%,根据文献[24]进行计算；k，m为Avrami常数，仅与材料的化学成分和变形量有关。

1 100 ℃，0.01 s-1条件下的峰值应变和临界应变分别为0.089 9和0.035 5。为了确定k和m的值，将式(13)变换为

ln[-ln(1-XDRX)]=lnk+mln[(ε-εc)/εp]

(14)

得到ln[-ln(1-XDRX)]-ln[(ε-εc)/εp]的关系曲线，如图5所示，可得lnk=-3.014，k=0.049；m=2.132。将k,m代入式(15)，得到再结晶体积分数随应变变化的Avrami模型为：

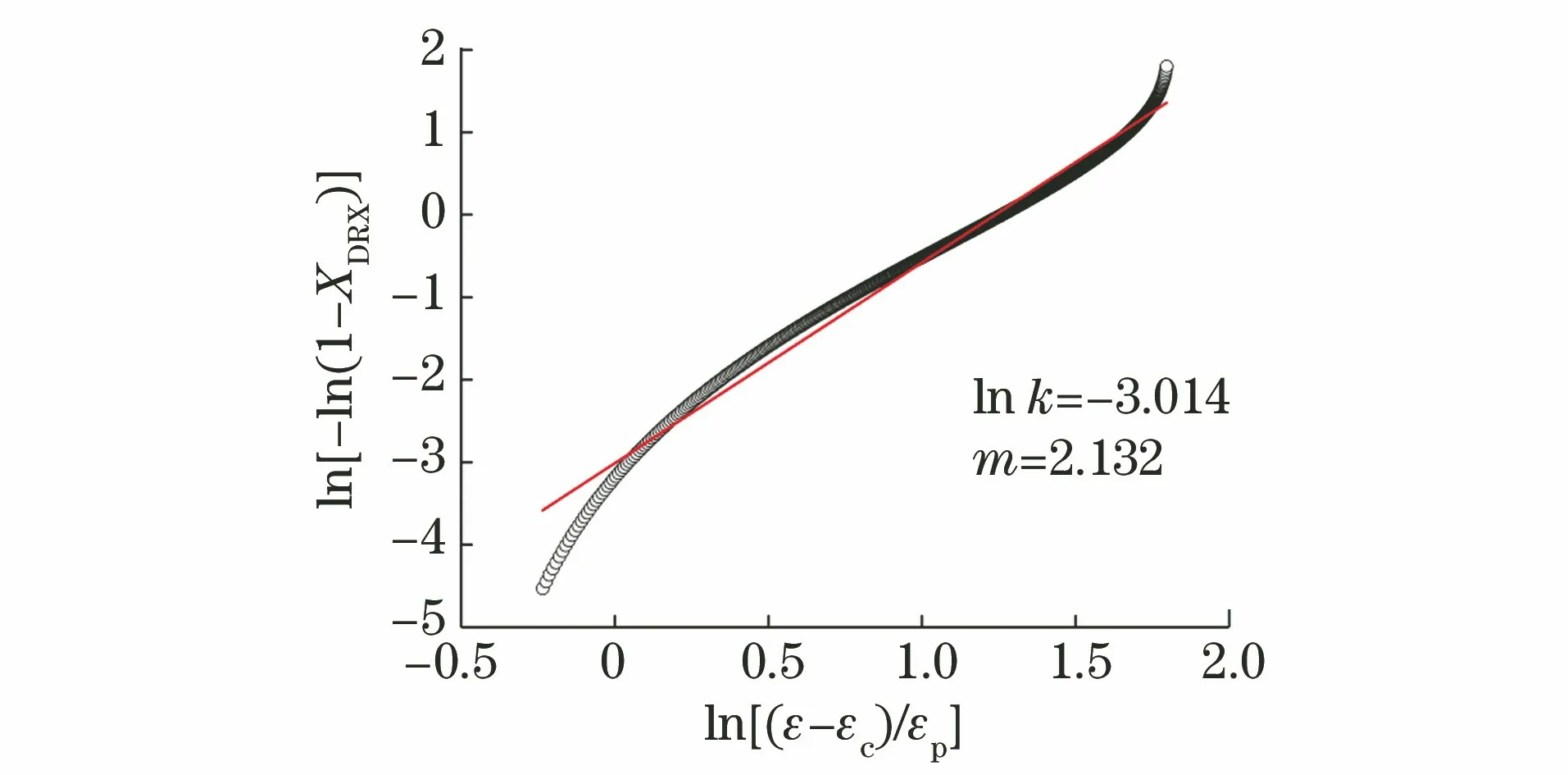
图5 ln[-ln(1-XDRX)]-ln[(ε-εc)/εp]关系曲线Fig.5 Curve of ln[-ln(1-XDRX)] and ln[(ε-εc)/εp]

(15)

3 结 论

(1) 在950 ℃，1 s-1变形条件下，GH4169高温合金呈不完全动态再结晶组织，温度升高或应变速率降低均使再结晶组织体积分数增加，合金的流变应力降低；在1 100 ℃，0.01 s-1条件下，再结晶晶粒长大。