直纹面侧铣加工精度可靠性分析
潘柏松,丁 炜,项涌涌,罗路平,俞铭杰
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
0 引言
直纹面是实际工程应用中常见的一种曲面类型,在汽轮机叶轮以及航天航空领域等关键部件中应用十分广泛。这类零件整体性能受实际加工精度影响大且具有复杂的几何形状。直纹面侧铣加工中存在随机不确定性、认知不确定性[1-2]和动态不确定性等因素,现有研究将动态不确定激励描述为随机过程[3]。分析影响实际侧铣加工过程中的不确定性因素,建立反映侧铣过程不确定性误差与加工精度映射的误差传递模型,对实现有效的精度可靠性分析和精度可靠度预测至关重要。
加工精度建模以刀触点或刀轴线精度[4-5]为指标,基于多体系统理论,运用多体运动学原理和体间变换方法描述设备各类不确定性误差与加工精度间的关系[6]。影响侧铣加工精度的不确定误差主要包括机床误差和加工过程误差,分别包括由机床部件几何误差引起的随机不确定误差,以及由运动参数和刀具、工件参数引起的动态不确定误差。近年来,国内外学者对以不确定性误差为基础的加工精度建模与可靠性理论展开了大量研究。余治民等[7]基于磨床综合几何误差传递模型建立了加工精度近似模型;Ding等[8]基于几何误差、工件定位误差以及刀具参数误差综合建立了五轴外圆铣削加工精度模型。与上述误差精度建模相比,侧铣加工精度建模仍需考虑随机过程动态不确定性因素导致模型非线性度增加的问题。机床加工精度可靠性研究主要分析方法有蒙特卡洛法、一次二阶矩法(First Order Reliability Method, FORM)、响应面法等[9]。以上方法需获得明确的极限状态函数且计算效率低,不适合求解带有随机过程不确定性变量输入的动态可靠性问题。随机过程往往带有时变特性,故又称时变可靠性问题[10]。针对这一类问题,在超越理论[11-13]与极值法[14-15]两个主要理论基础上,Andrieu-Renaud等[16]提出了PHI2方法及其改进方法;Jiang等[17]提出一种基于随机过程离散化的时变可靠性分析方法。两者有效地将动态可靠性模型求解问题转化为静态可靠性问题,但无法保证解决复杂模型的动态可靠性问题时的求解精度。Wang等[18]提出一种自适应极值响应面法的时变可靠性求解方法,计算结果更为精确,但多数情况下分析结果仍较难获得精确的极值响应分布。
为此,本文将综合考虑侧铣误差传递模型中存在的几何误差因素以及随机过程动态不确定性因素,应用动态可靠性方法对侧铣加工精度可靠度预测展开研究。基于两点偏置刀位算法并考虑刀具参数不确定性,获得以高斯随机过程表征的切触点坐标变化。建立了基于LU400型BC轴机床拓扑结构且综合考虑驱动误差的精度可靠度模型以及精度可靠度高斯过程(Gaussian Process,GP)代理模型。在少样本数据条件下,为保证可靠度计算精度,以模型精度指标迭代更新计算模型,基于更新后的高精度代理模型,运用蒙特卡洛法获得可靠度值。
1 侧铣精度可靠度模型
运用多体系统理论获得BC轴五轴机床误差传递模型,并量化侧铣加工过程中存在的各类不确定因素,建立了基于切触点GP模型的直纹面侧铣精度可靠度模型。
1.1 GP模型
GP模型可通过均值函数m(x)和协方差函数k(x,x′)来表示。在拟合噪声数据时,能够通过指定每个点的噪声方差来使用。带噪声的随机变量函数f(x)可由GP模型[19]表示为:
f(x)~GP(m(x),k(x,x′))。
(1)
式中:m(x)≜E(f(x)),k(x,x′)≜Σ(f(x),f(x′)),x′表示不同于x的测试样本点。
协方差函数也称核函数(kernel function)。典型的GP模型设均值函数为零,核函数为指数平方形式如式(2)所示:
(2)
式中l为由模型确定的长度参数。
由于GP建模的关键假设是分析数据可以表示为来自多元高斯分布的样本集,假设:
(3)
式中:T表示矩阵转置,y表示现有样本观测值,y*表示预测样本点x*估计值,相应符号表示如下:
K**=k(x*,x*)。
对测试样本范围内任意测试输入x*,高斯过程模型的预测分布可以表示为:
(4)
1.2 侧铣原理及切触点坐标GP模型
直纹面在工程运用中的矢量表达式如式(5)所示:
S(u,v)=(1-v)B0(u)+vB1(u)。
(5)
式中:B0(u)、B1(u)分别表示两条准线函数,u、v分别表示准线与直母线变量参数。相应示意图如图1所示。


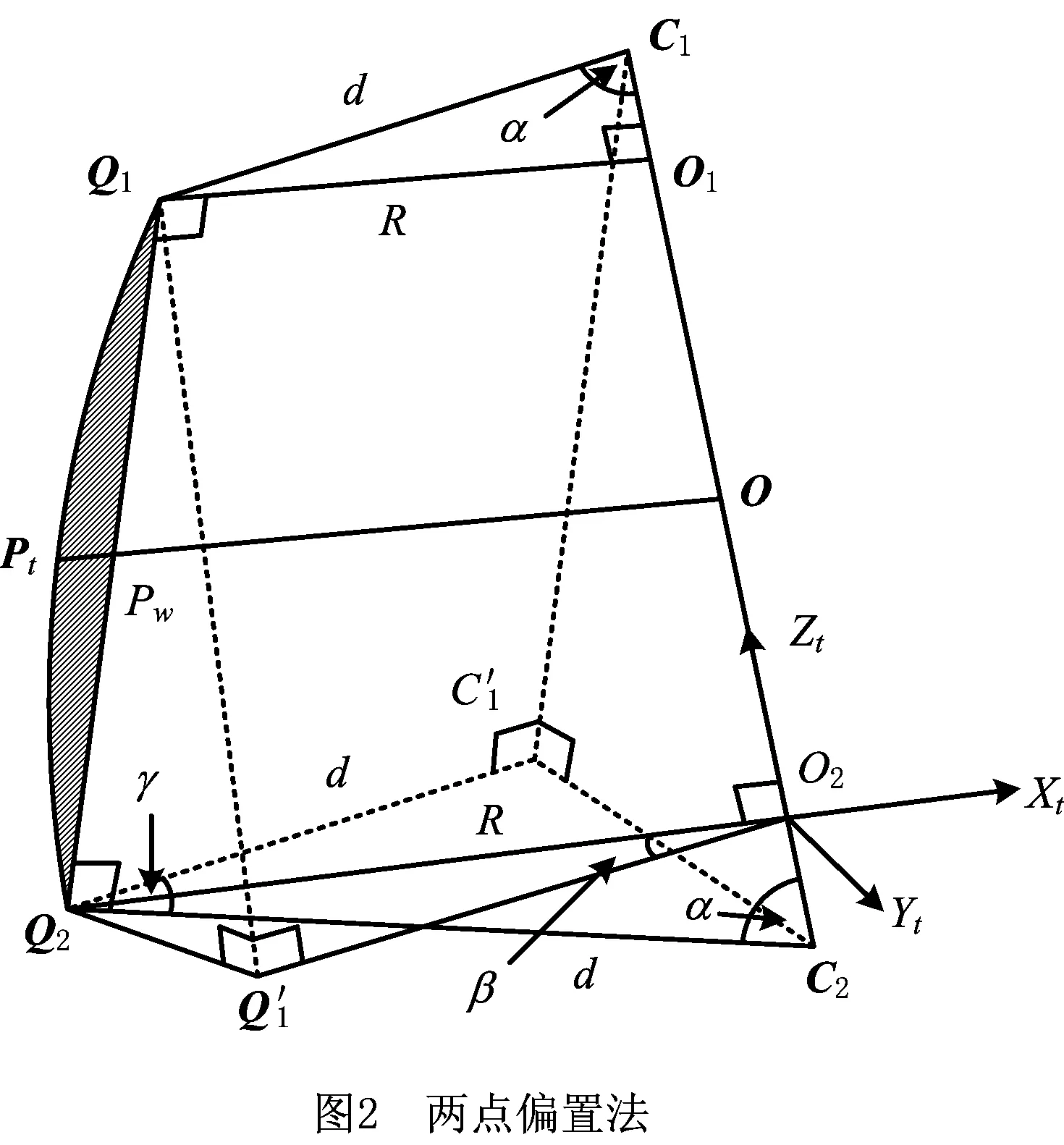
结合文献[20]中的推理,易证图中∠O1C1Q1=∠Q2C2O2=α,并通过数值迭代计算参数d、α的值,最终O1、O2的坐标如式(6)所示。O2为刀具端面中心,O1O2即为刀位矢量。
(6)
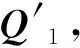
(7)

则最终获得螺旋线方程为:

(8)
已知在坐标系(xyz)t中Q1、Q2坐标,则可得直线Q1Q2的方程为:
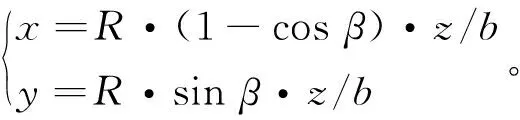
(9)
根据螺旋线方程和理想点直线方程Q1Q2即可获得理想参数下侧铣加工切触点坐标,两个坐标的空间距离即可表示原理误差值。设在刀具坐标系中,切触点坐标为Pt;工件坐标系中,理想点坐标为Pw。由于刀具半径不确定性项R、参与铣削刃长不确定性项b存在,且无法获得切触点坐标显式函数,以高斯随机过程表征的切触点坐标变化,即Y(s)~GP(m(s),k(s,s′))。本文用Pts(ptsx、ptsy、ptsz)表示刀具坐标系下x、y、z三个方向切触点预测坐标值。
1.3 直纹面侧铣精度可靠度模型
以LU400型BC轴五轴机床为加工设备分析,运用D-H矩阵[21]建立侧铣加工精度误差模型。机床结构示意图如图3所示。根据多体系统理论,相应BC轴机床拓扑机构图如图4所示。
误差建模通过齐次坐标变化来描述误差在不同坐标系中的转换,并通过特征矩阵来建立模型,即位置特征矩阵和姿态特征矩阵。结合相邻序体间的误差变换矩阵[22]可表示为:
Tij=Tij·pTij·peTij·sTij·se。
(10)
式中:Tij·p表示相对静止的理想静止特征矩阵,Tij·pe表示相对静止的静止误差特征矩阵,Tij·s表示相对运动的理想运动特征矩阵,Tij·se表示相对运动的运动误差特征矩阵。


驱动误差指机构动力源驱动误差,即机构驱动元件的输出误差[22]。本文模型考虑当工艺系统温度变化很小,且工艺系统的刚度可以忽略刚度误差。根据文献[22]的分析,所建模型条件可只考虑驱动产生的微小误差进行建模。而实际驱动误差测量结果也包含了其他误差源的影响,只是影响系数小。本文将机床绕Y轴转动和绕Z轴转动驱动力导致的驱动误差量分别定义为ΔβB、ΔγC,将机床导轨沿X轴、Y轴、Z轴平动时驱动力导致的误差驱动量分别定义为ΔxX、ΔyY、ΔzZ。坐标系设定过程中(如图3):将床身、立转台以及摆动转台的原点设定在摆动转台中心点O1;3个滑轨与主轴的原点设定在主轴端面中心点O2;刀具的坐标原点设定在刀具端面中心点处O3;工件坐标系原点设定在工件端面处O4。其中,O2点处的坐标系相对于O1点处的坐标系平移了矢量P1=(x21,y21,z21)T,O3点处的坐标系相对于O2点处的坐标系平移了矢量P2=(0,0,z32)T,O4点处的坐标系相对于O1点处的坐标系平移了矢量P3=(x41,y41,z41)T。获得如表1所示的体间特征矩阵,表中:Δz87为装刀后实测刀长方差;x、y、z、B、C为根据上节求得刀轴矢量,通过机床运动学反变换公式所求得各轴瞬时运动参数值,E表示单位矩阵。

表1 体间特征矩阵
设刀具切触点在刀具坐标系下齐次坐标为Pt=(ptx,pty,ptz,1)T,则高斯随机过程表征下切触点齐次坐标为Pts=(ptsx,ptsy,ptsz,1)。侧铣加工策略下,在工件坐标系下与加工成形点对应的理想加工成形点位置点齐次坐标为Pw=(pwx,pwy,pwz,1)T。利用特征矩阵,分别沿着刀具—床身和工件—床身的路线,将高斯随机过程表征的切触点坐标与理想点分别变换到基坐标系下,即可获得最终侧铣精度可靠度模型。
Ε=T01T12T23Pw-T04T45T56T67T78Pts
=(Ex,Ey,Ez,1)。
(11)

根据精度可靠性定义,在允许极限误差下精度可靠度模型状态函数如式(12)所示:
g(X,Y(s),S)=δ-E(Δ)。
(12)
式中:δ表示允许极限误差,X表示所考虑模型随机不确定性变量,S表示切触点允许范围。
2 基于GP模型的侧铣精度可靠度求解算法
2.1 随机过程预处理
运用K-L变换[23]将精度可靠度模型中随机过程变量Y(s)表征为一组具有相应随机系数的确定性函数。将切触点坐标在[0,S]上按位置节点离散成(s1,…,si,…,sn),其中任意si与sj间的协方差函数通过k(si,sj)表示,相应的协方差矩阵如式(13)所示:
(13)
显然Σ为对称的正定矩阵,可表示为Σ=Φ·I·ΦT。式(13)中:Φ是由特征向量组成的特征矩阵,I是包含相应特征值的对角矩阵,I=[I1,I2,…,In]。此时随机过程Y(s)可以通过带有随机权重Z的确定性函数的线性求和来重构,如式(14)所示:
(14)
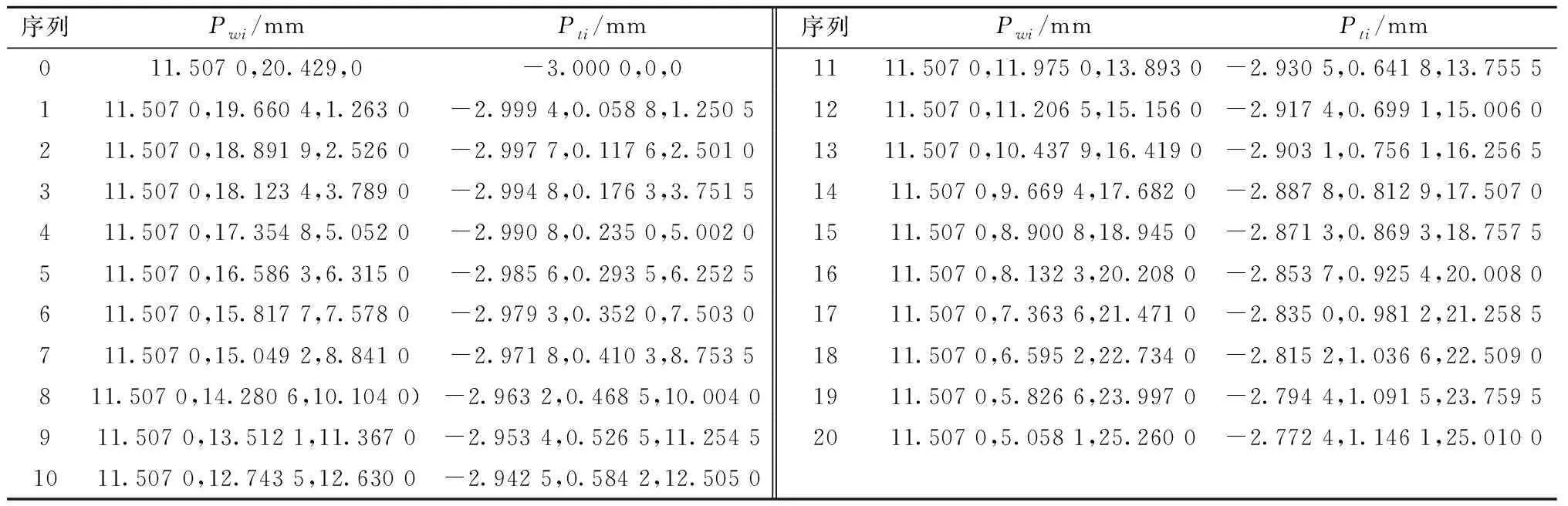
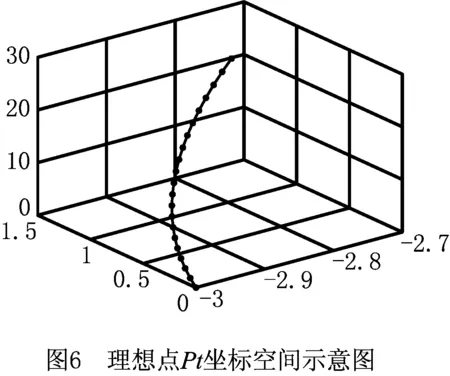
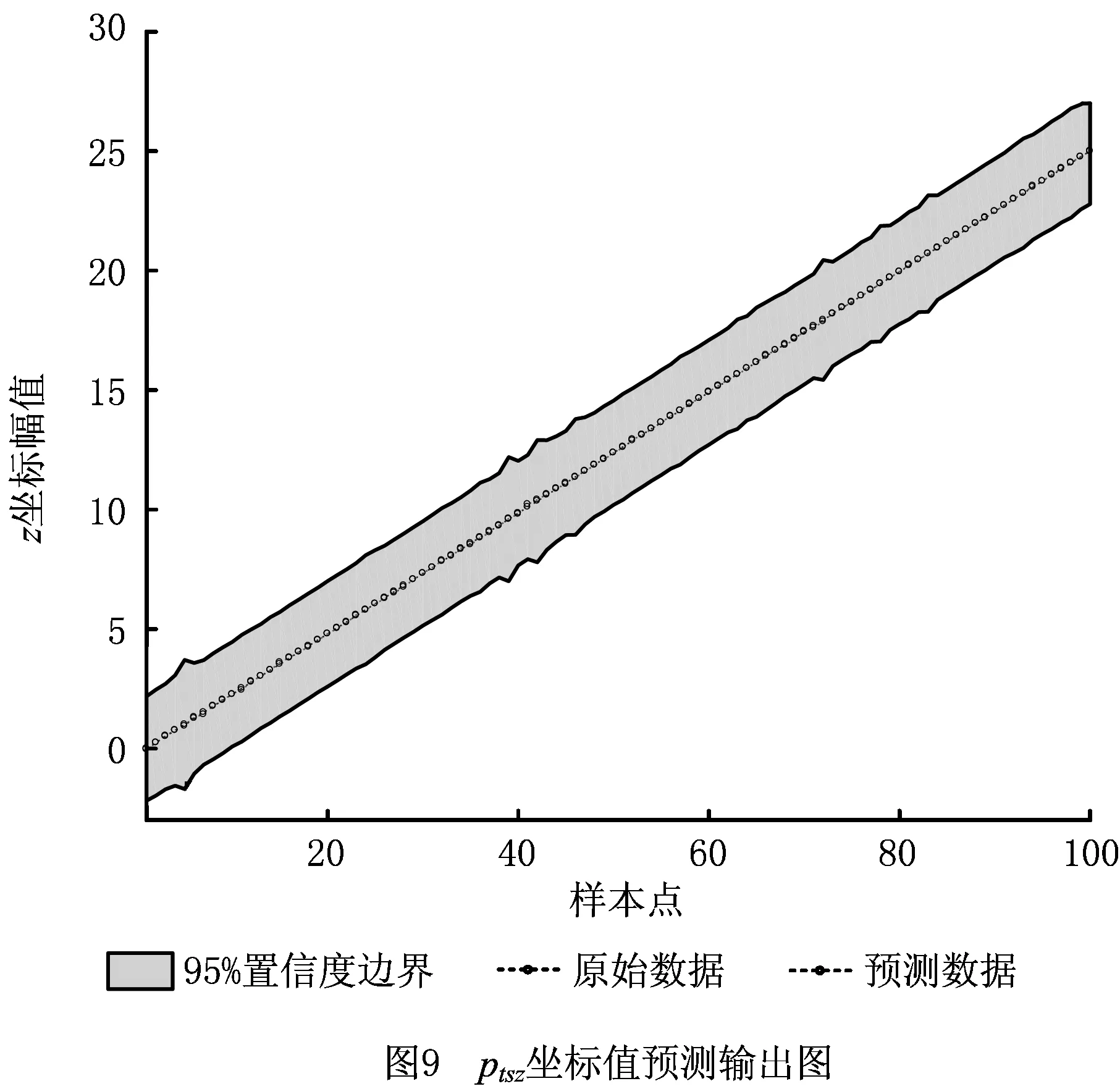
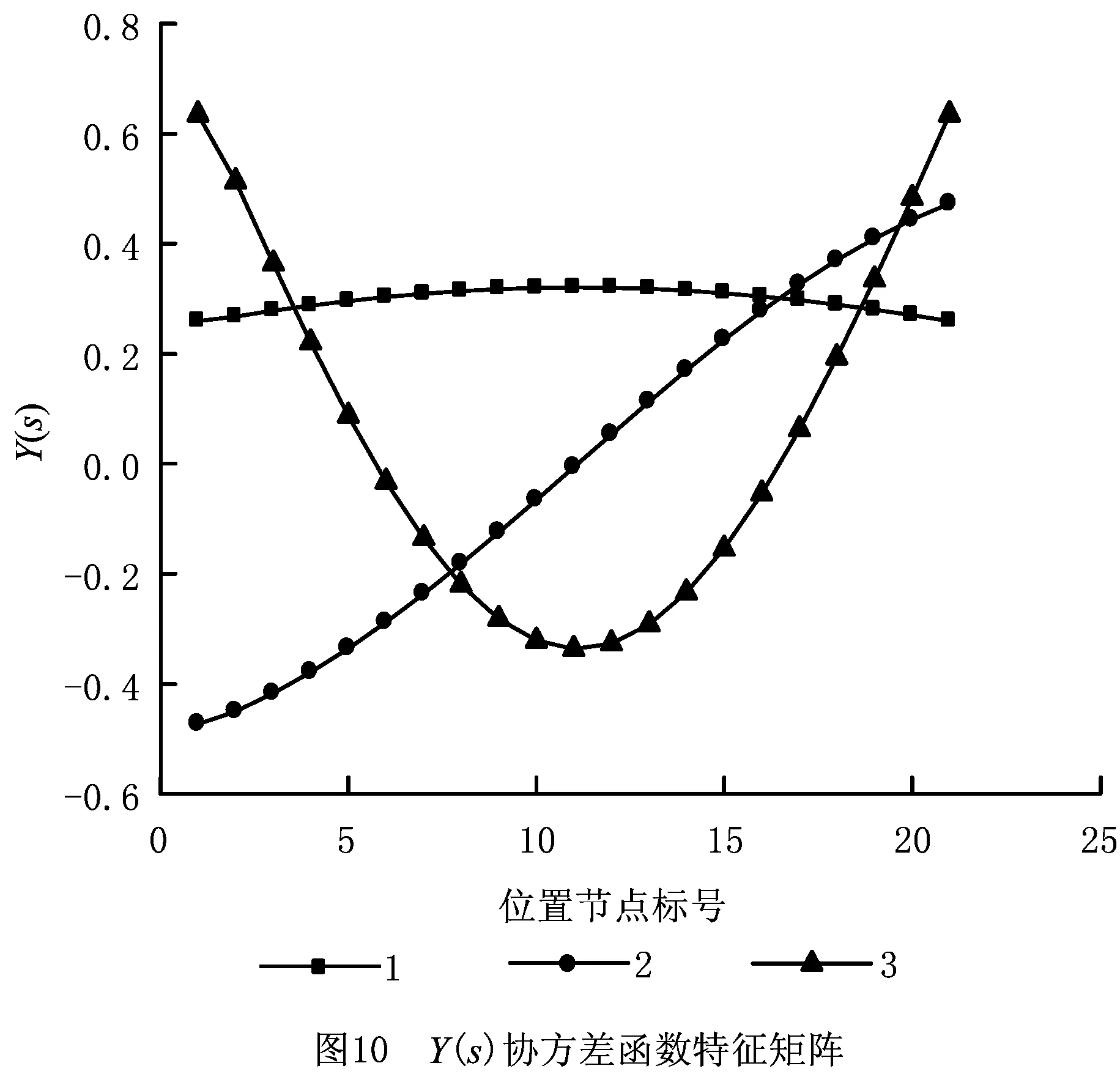
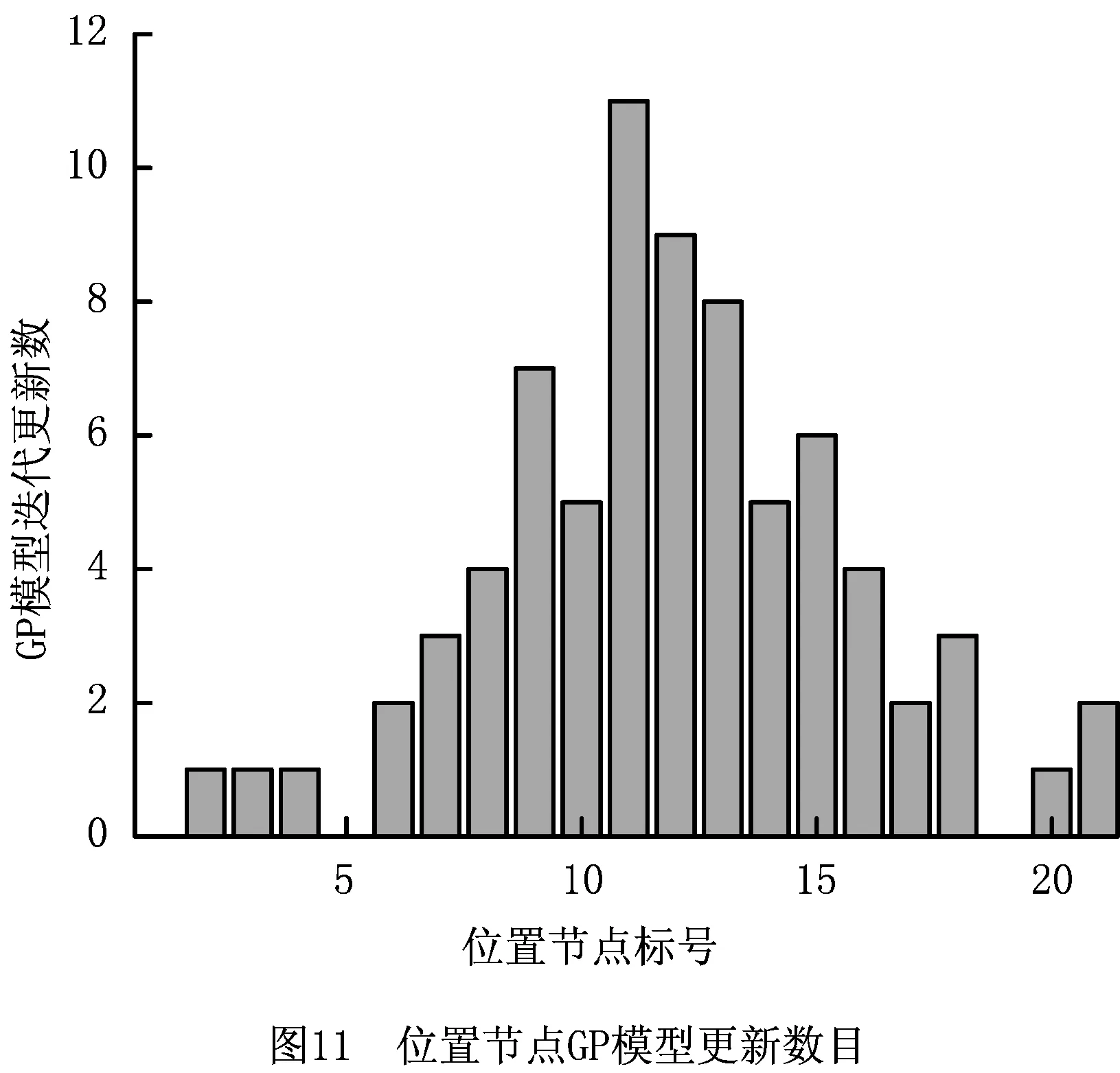
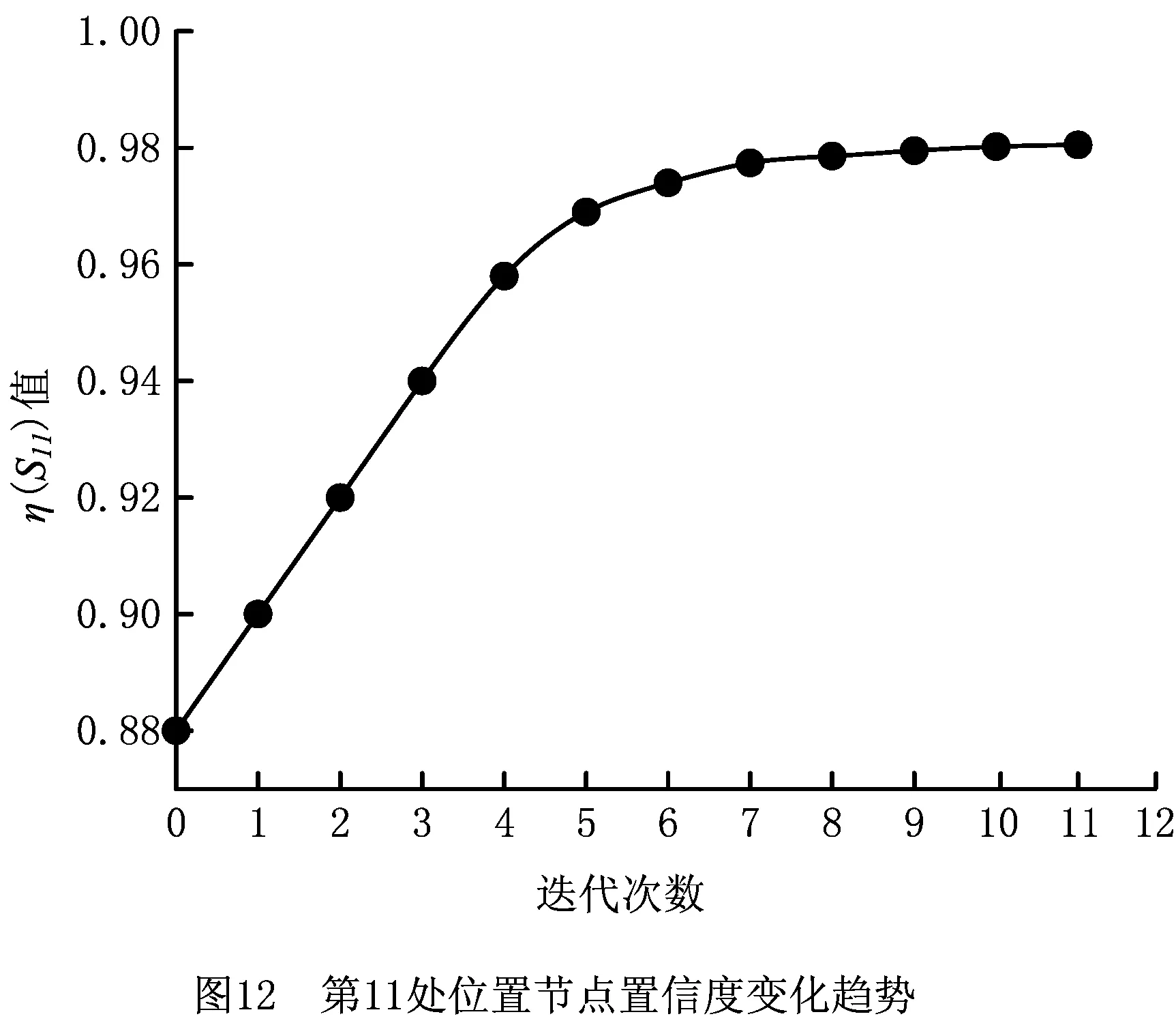
式中Z表示随机过程重构中的P个不相关的标准正态变量,Z=[Z1,…,ZP],且P (15) 式中临界阈值θ表示随机过程重构的精度阈值,一般设θ=0.95。 通过上述方法即可将随机过程Y(s)表示成P个带有相应权重的标准正态随机变量Z的线性求和,实现将带随机过程的输入[X,Y(s)]变换为[X,Z],Z=[Z1,Z2,…,ZP]。 刀触线上离散点超出精度阈值时,失效概率可表示为: Pf(0,S)=Pr(ge,S(X,Z,S)>0) (16) 为提高模型计算效率,通过构造一个位置节点GP代理模型来预测基于参数s的极限状态函数,并最终运用蒙特卡洛法来计算失效概率值Pf(0,S)。考虑预处理后模型输入均为随机变量,用W替代输入变量[X,Z],且W=[W1,W2,…,Wk,]。采用的相关函数如式(17)所示,其协方差可表示为Cov(i,j)=σ2C(i,j), C(i,j)=Corr(wi,wj)=exp (17) 式中au与bu是由高斯过程模型确定的参数值,且u=1,…,k。 假设当代理模型通过p个样本值时,其对数似然函数如式(18)所示: LGP=-1/2·[pln(2π)+plnσ2+ln|C|+1/(2σ2)· (G-Aμ)TC-1(G-Aμ)]。 (18) 式中:A表示p维的单位阵,G表示模型输入的训练观测值。 通过最大化对数似然函数来更新获取GP代理模型的超参数。并通过极大似然估计获得抽样数据下的GP模型,则可将新样本测试点w′的预测值表示为: gS(w′,si)=μ+rTC-1(G-Aμ)。 (19) 式中:μ为预测均值;r表示新样本测试点w′与训练样本输入值w=[w1,w2,…,wn]的相关向量,r(i)=corr(w′,wi)。 因此,节点处测试点预测值均方误差可以用式(20)表示: (20) 根据所构造GP代理模型以及式(19)获得设定样本预测值,第i个位置节点的指示函数如式(21)所示: (21) 计算模型可靠度值的精度取决于GP代理模型的精度,为实现少样本数据下获得精确的可靠度,通过设定代理模型精度指标以更新计算模型。由于模型预测的不确定性,将si节点上样本点wi正确预测的概率定义为Pc(wi,si),如式(22)所示: (22) 结合文献[25]将代理模型更新条件精度指标定义为节点上样本预测概率的期望,当输入m个有效样本时,如式(23)所示为节点si下代理模型精度指标。一般将η值设定为[0.95~1],其值越大表示模型精度越高。 (23) 同时,为了在连续迭代过程中获得有用的样本点来更新代理模型,将新样本点的重要性指标定义为φ(wi,si),如式(24)所示: (24) 在位置节点si处,通过最大化φ值可获得该位置节点处的有用样本点,如式(25)所示,用于更新代理模型,直至满足代理模型精度指标η(si)。 (25) 对于单个刀位下整条刀触线上的可靠度计算,其可靠度随直纹面参数v的变化而变化。设v=S,则该刀触线上可靠度可表示为 =E[I(w)|[0,S]]。 (26) 式中:I(w)|[0,S]表示n个位置节点上由相应的n个GP模型近似的预测响应值的指示函数,如式(27)所示: I(w)|[0,S]= (27) 式中gs(w,si),1≤i≤n表示si位置节点处n个由GP模型近似所得预测值。 当使用蒙特卡洛法进行N次抽样后即可求得在整条切触线上的可靠度值,即精度可靠度值R(0,S): (28) 根据以上分析,所提算法流程图如图5所示。 具体步骤如下: 步骤1初始化。采用输入位置表征S的范围值,初始化位置节点数s,置信度目标值η;对随机过程Y(s)进行K-L变换分解,输入用于构建GP模型的训练样本数,将随机过程Y(s)表示成P个带有相应权重的标准正态随机变量Z的线性求和。 步骤2根据已有数据集构建一个位置节点GP模型来预测基于s的极限状态函数。将刀触线按位置节点离散si,并对预处理后W变量采样n个样本点,计算每个离散节点上的响应值,构建所有位置节点的GP模型,等待训练点更新模型。 步骤3更新模型超参数。根据初始输入的样本点可获得初始超参数值,模型加入新样本点后对所有样本点的预测代理模型进行最大化对数似然函数,即可获得新的GP模型的超参数,从而更新预测模型。 步骤4GP代理模型精度计算。由于模型预测的不确定性,根据模型精度指标η更新代理模型;对于每个位置节点,通过最大化样本重要性指标φ(wi,si)的值来确定新样本点。并运用输入新样本点预测值更新GP模型超参,直到满足代理模型精度阈值,否则返回步骤2。 步骤5计算加工精度可靠度值。运用蒙特卡洛法进行N次抽样,计算获得GP代理模型预测值的指示函数I(w)|[0,S]的值,根据式(28)即可求得在整条切触线上的可靠度值R(0,S)。 基于LU400型五轴数控机床,通过建立侧铣加工精度可靠度模型,以文献[26]中设计曲面为例进行算法验证分析。根据曲面精度等级要求设定允许极限误差的均值和标准差分别为μ0=0.02,σ0=0.008。本算例采用直径为6 mm的立铣刀,非可展直纹面参数方程为: B0(u)=[u20.429 0], B1(u)=[u0.0382u233.995], u∈[0,23.014],v∈[0,1]。 取u=11.507处直母线,等分离散位置节点,节点数n=21。数值计算Pwi与Pti相应的坐标值,Pwi、Pti分别表示对应节点下的切触点与理想点理论坐标值,如表2所示。表3为求解切触线位置参数过程中的中间参数值。 表2 抽样切触点与理想点位置坐标值 表3 中间参数计算值 理想侧铣参数下切触点空间位置如图6所示,图中三维空间中的点即切触线上等分离散点在刀具坐标下的空间示意,具体数据如表2中Pti所示。由于引入不确定性项R、b,且迭代计算过程无法获得显式函数,以高斯随机过程Y(s)表征切触点坐标变化,用Pts(ptsx、ptsy、ptsz)表示刀具坐标系下x、y、z三个方向切触点预测坐标值。在实际工程中,可以获得刀具半径误差数据,参与铣削侧刃长度则应根据实测曲面参数确定。后者在实际过程中检测困难,本文由某企业代加工,并通过三坐标测量机检测获取训练与测试样本数据。为获得足够精确的预测数据,本算例2×104组训练数据来进行模型预测,为体现数据变化过程离散抽取实测数据中102数据样本作为测试数据,经数据分析后所选取的训练数据以及测试数据的样本量能满足预测要求。 为获得预测坐标值Pts的变化趋势,本文采用z-score标准化处理(正态标准化)对GP代理模型中随机过程变量Y(s)的测试与训练数据进行标准化处理,并采用零均值、平方指数核函数模型预测Pts坐标的变化,即ptsx、ptsy、ptsz三个输出量的变化,如图7~图9所示。图7中通过高斯随机过程Y(s)表征的切触点X轴坐标,即ptsx,通过100个测试样本点的预测响应值来表示,由图7可知,在设定目标置信度95%范围内,预测数据波动小,有效降低了训练数据中过大的幅值波动,剔除了数据获取随机性引起的部分失效数据,同时保证了后续样本点抽样的数据稳定。同理,图8与图9分别为利用高斯随机过程Y(s)表征的切触点Y轴与Z轴坐标,由图可知,ptsy与ptsz相较于ptsx在95%置信度范围下数据波动幅度更小,说明预测响应值更接近训练数据的变化趋势。 为尽可能覆盖随机过程Y(s)的变化过程,采用K-L变换来实现随机过程数据的重构与降维。当P=3时,对应特征向量的特征值为0.008 6,根据式(15)计算左侧式为0.961>0.95,故满足判断条件。将标准正态变量Z=[Z1,Z2,Z3]作为系数的3个最重要的特征函数包含在展开式中。如图10所示,不同图形节点的三条散点线依次表示数据重构后,带有随机权重的变量Z1、Z2、Z3的相应位置节点下的特征函数值。根据文献[24]中重构变量数P的确定方法,此时重构后变量Z的确定性函数能够捕捉到随机过程Y(s)的变化过程。通过特征函数简化带随机过程的输入[X,Y(s)],使后续分析模型输入变量均为随机变量输入。 上述步骤完成了对输入变量的预处理和数据重构。加工过程中引起的随机误差主要为驱动力误差,需作为后续可靠度计算的计算变量,为获得驱动力带来的误差,即由单个轴驱动产生的微小误差。本文算例中,LU400型数控机床规格参数如表4所示,数控机床的实际驱动误差分布如表5所示。为计算最终加工精度响应模型,两点偏置法下获得刀位数据后,根据现有运动学反变换公式求解获得各运动轴位置坐标如表6所示,且表中后3项为模型计算所需参数常量,根据实际加工坐标系设定条件确定。 表4 机床规格参数表 表5 驱动误差分布 表6 计算中间量参数 算法通过在位置节点建立GP模型并通过极大似然估计来获取重要样本点。获取一定数量新样本点后更新模型及模型参数,直至满足预测阈值η(si),本算例设定为0.98。图11表示在模型更新过程中不同位置节点GP模型迭代数目。图12以第11处位置节点为例,表示节点GP模型更新过程中模型精度指标η的变化趋势,当阈值连续大于0.98时更新结束,由图12可知当迭代次数到达10、11次时,连续大于0.98,则迭代结束。 最终运用指示函数通过蒙特卡洛法抽样计算最终可靠度值R(0,S)。根据本文算法求得侧铣加工精度可靠度如表7中所示,节点范围表示指定母线参数系数下的节点区间,表中Nc表示本文方法模型状态函数调用次数以及传统蒙特卡洛法模型状态函数调用次数,迭代数表示本文方法代理模型更新迭代数。分析表7可知,与传统蒙特卡洛法相比,所提出的方法在保证可靠度预测精确性同时,可明显提高计算效率。根据图13,在直母线参数为1的情况下,可知随着计算位置节点范围增大,失效概率先增大后渐趋于平缓,与传统方法变化一致,实现了在该侧铣策略下直纹面连续位置节点上加工精度可靠度的预测。 表7 加工精度可靠度对比 本文建立了考虑机床驱动误差与刀具参数不确定性的侧铣加工精度可靠度模型。以高斯随机过程表征切触点坐标变化,基于LU400型BC轴机床误差传递模型,利用多体系统理论获得了精度可靠度模型,为加工精度可靠性分析打下了基础。建立了基于GP模型的侧铣精度可靠度代理模型。运用K-L变换对随机过程变量预处理并建立了切触点位置节点GP代理模型,根据代理模型精度定义与模型精度阈值η更新获得了高精度代理模型。 基于更新后的高精度代理模型运用蒙特卡洛法计算加工精度可靠度,计算结果与传统蒙特卡洛法相比,有效预测了切触线上精度可靠度的变化趋势,在保证可靠度预测精确性的同时,可明显提高计算效率,为直纹面侧铣加工精度可靠度预测提供了有效的方法。当模型数据量少时,基于GP模型预测可提供有效精度分析方法,以此为基础,未来将拓展对机床加工精度预测的分析研究。
2.2 精度可靠度GP代理模型
2.3 代理模型更新及可靠度求解


3 算例研究








4 结束语

