局部稀疏函数型聚类及其在经济增长模式分析中的应用
方匡南,蒲 丹,张庆昭,1c,王呈斌
(1.厦门大学 a.经济学院,b.计量经济学教育部重点实验室,c.王亚南经济研究院,福建 厦门 361005;2.台州学院 浙江(台州)小微金融研究院,浙江 台州 318000)
一、引 言
国内生产总值(GDP)作为衡量一个国家或者地区经济发展水平的重要指标,对其进行分析和研究,一直是经济领域的热点问题。不同国家或者地区由于地理位置、资源优势、历史因素和地方政策等原因,经济发展水平参差不齐,经济发展模式也不尽相同。基于不同国家或地区的GDP数据进行聚类分析,将具有相同经济发展模式的国家和地区聚为一类,有利于人们对不同的经济发展模式进行研究,也有助于政府因地制宜制定经济政策,改善地区经济发展不平衡的现象,促进国家或地区经济健康持续快速发展。
不同于之前将观测值视作时间序列进行研究,函数型数据分析(Functional Data Analysis,简称FDA)以“化数为形”为基本特征,发掘原始统计数据所蕴含的函数规律和由函数规律引发的计算和分析活动[4]。FDA秉承“化零为整”的大数据分析思想,将在时间或者其他维度上观测的离散序列视为具有统一内在结构的连续平滑函数进行统计分析,不仅需要较少的假设条件,适用范围更广,而且能够挖掘出潜在的动态信息,这使其成为了近年来的研究热点[5]。不少学者将FDA应用于GDP数据,将历年的GDP数据视为具有函数性质的序列,对各个国家或地区进行聚类分析。程豪等通过函数型聚类方法对中国不同省份的GDP发展速度进行聚类,发现江苏、山东、广东三个省份的GDP最具发展潜力[6]。高桃璇等通过GDP等5个经济指标应用函数型数据聚类对中国31个省份进行了经济区域的划分,不仅打破传统的基于地理位置的划分,而且充分考虑了各省份的产业结构[7]。函数型聚类不仅适用于GDP数据,在金融学、气象学等领域也得到广泛的应用[8-9]。
函数型聚类方法大致分为三类[10]。第一类是两步法,即先通过基函数对函数降维,然后对基函数的系数应用传统的聚类方法。常用的基函数有B样条基函数、傅里叶基函数、高斯基函数、小波基函数和主成分基函数[11-14]。第二类是先定义准则用于衡量函数型数据之间的距离或者相似性,再应用传统的基于距离的聚类方法[15-16]。第三类是基于模型的聚类方法,即对基函数展开的系数或者主成分得分进行不同的模型假设。James和Sugar在处理稀疏不规则函数型数据时,假设B样条展开的系数服从随机效应模型[17]。Jacques和Preda在处理单变量和多变量函数型数据时均假设主成分得分服从高斯混合模型[18-19]。
在实际的函数型数据聚类分析中,可能部分区间的函数决定了聚类结果,而另外的区间对聚类的结果影响不大,甚至没有影响。因此,利用函数型聚类方法进行探索性分析时,除了关注聚类的结果,了解哪部分区间真正影响聚类结果,这有助于进一步分析。此外,使用噪音区间提供的信息不仅会影响到聚类结果的准确性,而且使聚类结果方差很大,导致聚类结果不可靠。因此,一些学者提出了局部稀疏的函数型聚类。局部稀疏的函数型聚类指在不牺牲聚类效果的情况下,在聚类时使用部分区间的信息而非全部区间的信息,即假设部分区间在聚类时作用很小,其提供的信息会干扰聚类的结果,降低聚类的质量。局部稀疏的函数型聚类在保证聚类效果的同时能有效区分稀疏区间和真正影响聚类结果的非稀疏区间,聚类结果的可解释性很强,更易于理解。目前关于局部稀疏的函数型聚类研究很少。
本文在稀疏K-means聚类的基础上,提出了局部稀疏函数型K-means聚类[20]。本文的创新主要有:第一,本文对函数型数据进行聚类,并同时实现稀疏区间的识别,不仅聚类效果好,而且结果具有更好的可解释性;第二,基于B样条对离散数据函数化,相比于Floriello和Vitelli提出的SFKmeans普适性更高,同时将基函数的稀疏性与子区间的稀疏性相互联系,方法直观形象[21];第三,将本文所提出的方法应用到中国31个省份1979—2018年的GDP数据中,将离散数据函数化,基于数据驱动的方式对各省份的经济增长模式进行研究。
二、局部稀疏函数型K-means聚类
函数型数据通常是连续函数在特定时点上的观测值,因此局部稀疏函数型K-means聚类的第一步是由离散的观测序列估计出潜在的函数形式。假设样本i(i=1,2,…,n)在时点{til∶l=1,2,…,Ti}对应Ti个观测值{yil∶l=1,2,…,Ti},观测值存在观测误差,潜在的函数形式为fi(t)(i=1,2,…,n)。因此,
yil=fi(til)+εil(l=1,2,…,Ti)
其中,εil(l=1,2,…,Ti)表示观测误差,彼此之间独立。本文允许不同函数在不同时点上观测取值,适用范围更广。为了估计出fi(t)的函数形式,通常假设fi(t)可由一组基函数展开。考虑到B样条基函数的灵活性和对于样本点敏感等诸多特性,本文选择B样条基函数作为基函数。假设B样条基函数定义在区间T=[a,b],a=e0
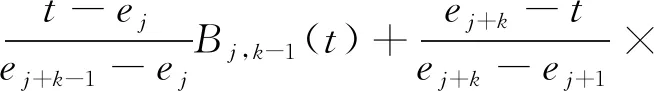
Bj+1,k-1(t)(k>1且k∈N)
给定节点序列τ和基函数的阶数m,即可确定一组B样条基函数。假设B样条基函数B(t)=(B1,m(t),B2,m(t),…,Bd+m,m(t))T,B样条系数βi=(βi,1,βi,2,,…,βi,d+m)T,则函数fi(t)可以表示为:
通过最小二乘的分析,βi的估计值为:
(1)
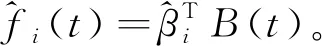
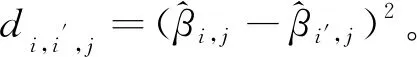
根据局部稀疏函数型聚类的定义,部分区间在聚类时作用很小。直观地理解,各个类在这部分区间上的函数取值或者形状差异很小,甚至没有差异。考虑到函数与B样条基函数的关系,这部分区间所对应的B样条基函数的观测值在各类之间差异也很小。因此基于Witten和Tibshirani提出的稀疏K-means聚类,本文对不同的基函数赋予不同的权重,使得加权后的组间距离之和(Weighted BCSS)最大,即同时寻找一个权重向量w=(w1,w2,…,wp)和一个样本的划分C={C1,C2,…,CK}极大化加权的组间距离之和,目标函数的具体形式如下:
s.t.‖w‖2≤1,‖w‖1≤s,wj≥0
j=1,2,…,p
(2)
其中s为超参数,wj表示第j个基函数在聚类时的权重。如果第j个基函数在聚类时很重要,则赋予的权重大;如果第j个基函数在聚类时作用不大,则权重很小甚至为0。
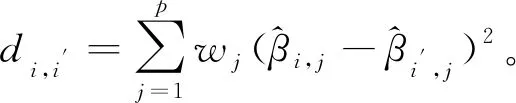
根据B样条基函数的定义,基函数Bj,m(t)(j=1,2,…,d+m)至多在m个子区间非负,在每一个子区间[ej,ej+1)上至多有m个阶数为m的基函数非零。因此,如果子区间[ej,ej+1)上所有非零基函数的权重都为零,那么该子区间权重为零,否则该子区间的权重非零。所有权重为零的子区间的集合即为稀疏区间的一个估计。
局部稀疏函数型K-means聚类算法步骤如下:
1.给定收敛精度、基函数阶数m和节点序列τ,确定基函数B(t)=(B1,m(t),B2,m(t),…,Bp,m(t))T;
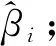
3.迭代求解式(2),得到样本划分C={C1,C2,…,CK}和权重w=(w1,w2,…,wp),具体为:
ii.固定权重w=(w1,w2,…,wp),求解样本划分C={C1,C2,…,CK};
iii.固定样本划分C={C1,C2,…,CK},求解权重w=(w1,w2,…,wp);
iv.重复步骤ii至iii直至收敛。
4.对于j=0,1,…,d,如果子区间[ej,ej+1)对应的非零基函数的权重均为零,则[ej,ej+1)属于稀疏子区间,否则不属于稀疏子区间。
通过以上算法求解,收敛得到的样本划分和所有稀疏子区间的集合即为最终的聚类结果和稀疏区间的估计。步骤3可用R语言中的sparcl包实现。步骤4可以预先设定一个很小的阈值,如果子区间[ej,ej+1)对应的非零基函数权重均小于给定阈值,则属于稀疏子区间,否则不属于稀疏子区间。
三、模拟分析
为了检验局部稀疏函数型K-means聚类的效果,本文进行了蒙特卡罗模拟分析,分别考虑了不同方差、不同分布、不同类别数以及不同类别的函数是否在多个子区间显著不同的情况。
(一)数据产生与设置
例1:本组模拟设置沿用了Floriello和Vitelli提出的模拟设置,共有两类曲线,每类曲线各生成100条[21]。由于SFKmeans方法的局限性,每条曲线均等距生成200个观测值。两类曲线分别由以下函数族生成,
f1(x)=[bsin(bπx)+a](a-4x)+c1,x∈[0,1]
f2(x)=
其中a~N(3,0.52),b~N(2,0.252),c1~N(0,0.52),c2~N(0.5,0.52)。d控制了两类曲线的重合比例。如果d越大,两类曲线重合的比例越高,局部稀疏性表现越明显。同时本组模拟考虑方差较大时各个方法的表现,设置a~N(3,0.52),b~N(2,0.52),c1~N(0,1),c2~N(0.5,1)。
例2:在例1的基础之上,本组模拟考虑三类曲线,每类曲线各生成100条。每类曲线分别由以下函数族生成,
f1(x)=[bsin(bπx)+a](a-4x)+c1,x∈[0,1]
f2(x)=
f3(x)=
其中a~N(3,0.52),b~N(2,0.252),c1~N(-0.5,0.52),c2~N(0.5,0.52)和c3~N(0,0.52)。在上述模拟设置的基础之上,本组模拟也考虑了方差较大时的情形,即a~N(3,0.52),b~N(2,0.52),c1~N(-0.5,1),c2~N(0.5,1),c3~N(0,1)。
例3:本组模拟考虑不同类别的函数在多个子区间上存在显著不同,分别考虑了类别数为两类和三类的情况。当类别数为两类时,每类曲线各生成100条,分别由以下函数族产生:
其中a1~N(1,0.752),b1~N(2,0.752),c1~N(1,1),a2~N(-1,0.752),b2~N(-2,0.752),c2~N(0,1),i1和i2控制了两类曲线重叠的比例。如果i1越小,i2越大,则两类曲线重叠的比例d=i2-i1越大。本文中i1依次设置为{0.05,0.15,0.25,0.35,0.45},i2对应设置为{0.95,0.85,0.75,0.65,0.55}。当类别数为三类时,每一类曲线由以下函数族产生:
x∈[0,1]
其中a1~N(1,0.752),b1~N(2,0.752),c1~N(1,1),a2~N(-1,0.752),b2~N(-2,0.752),c2~N(-0.5,1),c3~N(0,1)。
例4:在例3类别数为两类的模拟设置基础之上,本组模拟考虑ci为非正态分布的情况。模拟设置中假设c1和c2均服从自由度为3的t分布,其他设置与例3相同。
(二)模型评价和结果分析
为了验证本文方法的优劣,与不同的方法进行比较,分别为Floriello和Vitelli提出的SFKmeans、Abraham等提出的基于B样条基函数的函数型K-means聚类(Skmeans)、基于主成分得分的函数型K-means聚类(Pkmeans)、基于半度量距离的K-means聚类(SemiKmeans)与层次聚类(Semihclust)和Bouveyron和Jacques提出的funHDDC[21-22]。
B样条基函数由以下方式确定:在区间上等距选取71个节点,固定基函数的阶数为4阶。主成分的个数由累计方差贡献率大于90%决定。选择兰德指数(Rand index)和调整后兰德指数(adjusted Rand index)作为评价指标,用于衡量模拟估计的聚类结果和真实聚类结果的相似性。兰德指数在0到1之间取值,而调整后的兰德指数在-1到1之间取值。兰德指数和调整后兰德指数的值越大,表示估计聚类结果和真实聚类结果越相似。本文中每组模拟实验均进行100次模拟,然后分别计算两个指标的均值和标准差,部分结果如表1~4所示。
由表1~4可知,与其他非局部稀疏的方法相比,当曲线重叠比例d比较小时,本文提出的方法表现不逊于其他方法,而随着曲线重叠比例d逐渐增大,兰德指数和修正后的兰德指数逐渐下降,本文提出的方法逐渐优于其他非局部稀疏的方法。在例1和例2的设置下,当曲线重叠比例d=0.9时,本文提出的方法对应的兰德指数显著高于其他方法。这说明局部稀疏函数型K-means聚类在数据具有局部稀疏结构时表现很好。与局部稀疏的方法SFKmeans相比,本文提出的方法表现不逊于SFKmeans,兰德指数和修正后的兰德指数方差更小。综上所述,当数据具有局部稀疏结构时,本文方法的表现优于其他方法。
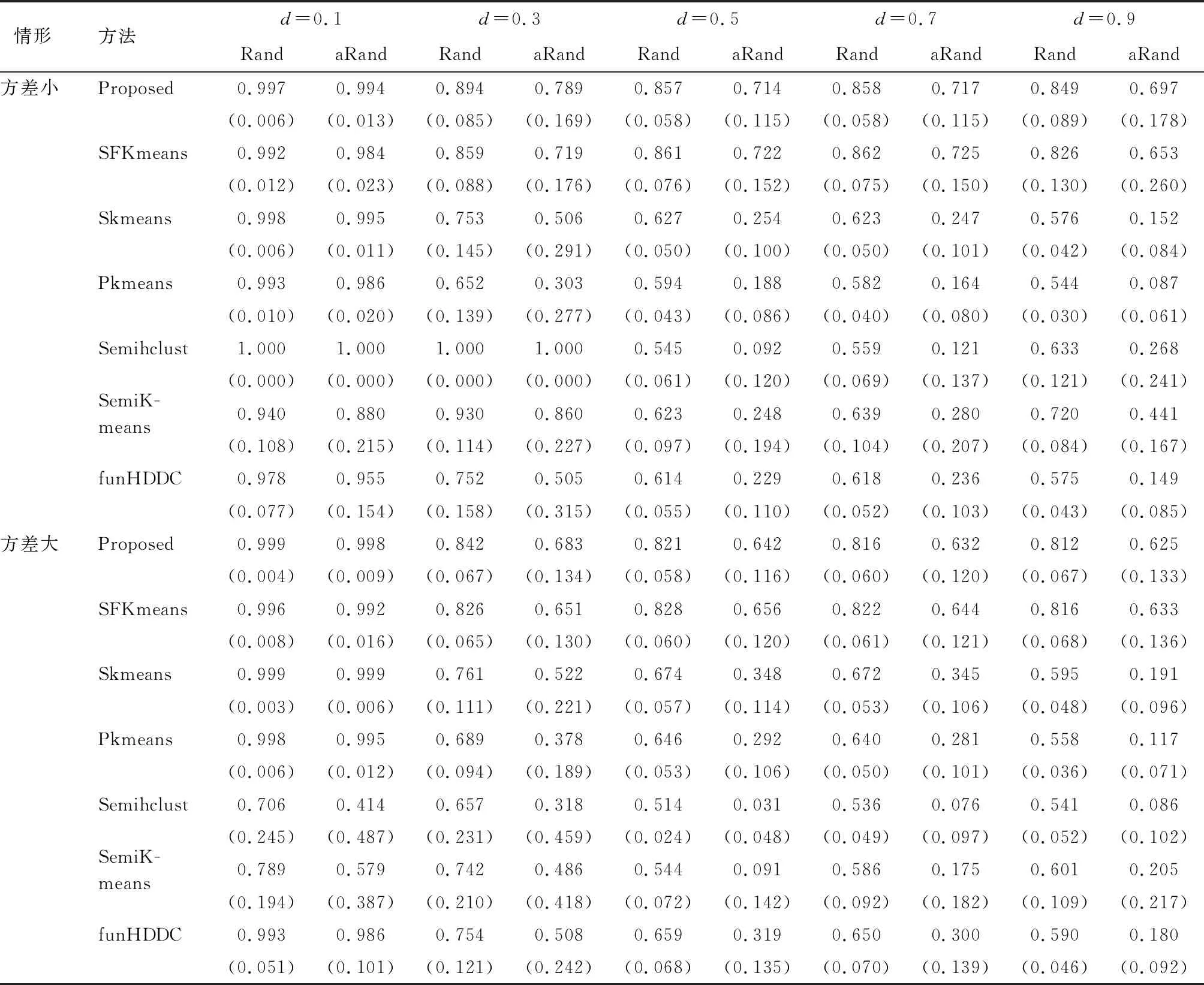
表1 模拟一的结果
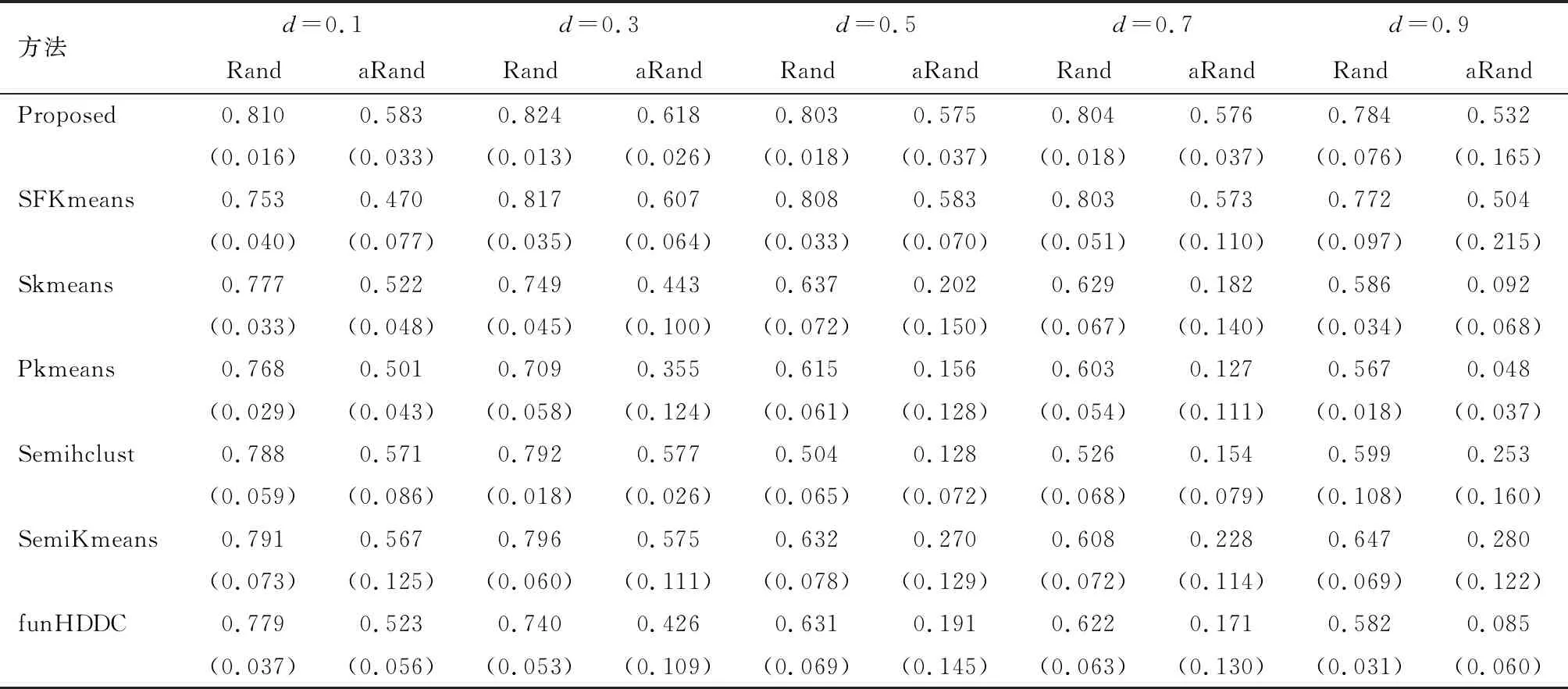
表2 模拟二的结果(方差小的情形)
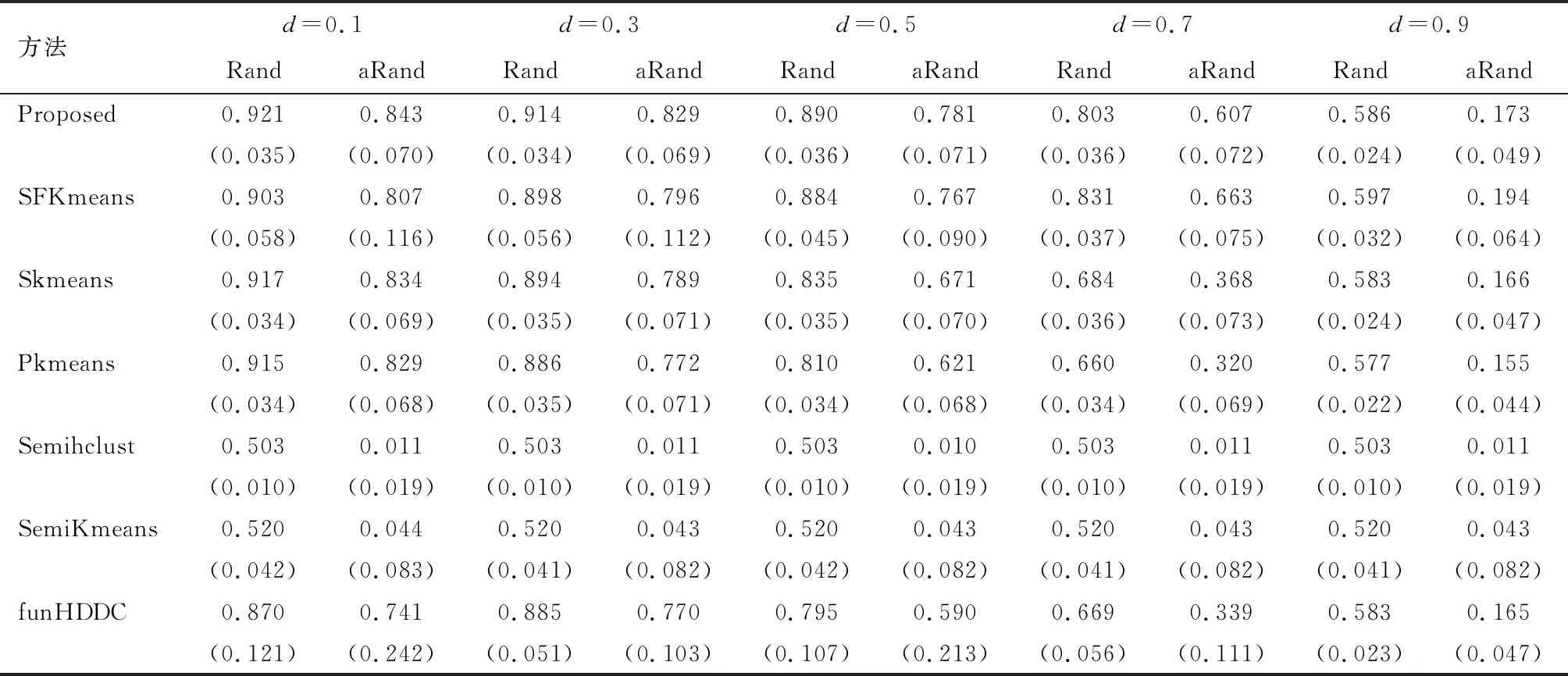
表3 模拟三的结果(类别数为两类的情形)

表4 模拟四的结果(ci服从t分布的情形)
四、实证分析
自1978年实行改革开放以来,中国经济高速增长,创造了举世瞩目的成绩,成为了世界第二大经济体。在经济发展的过程中,由于不同地区的地理位置、资源优势和政策支持的力度不同,各地区的经济发展情况千差万别,区域发展较为不平衡。沿海地区快速发展,人们的生活水平接近甚至达到了发达国家水平,而中西部的部分地区仍然较为落后,教育、医疗等资源缺乏,不同地区的经济发展情况存在着较大的差异。经济发展不平衡不仅会制约中国经济健康持续快速发展,而且会导致贫富差距加大,严重的甚至会激发社会矛盾,引起社会动荡。
中国各地区的经济发展情况差异巨大,经济增长模式也不尽相同。目前大多研究是从地域的角度对各区域的经济增长规律及模式进行定性分析,这存在许多不足。本文主要从定量的角度基于数据驱动对各省份的经济增长模式进行研究。GDP作为衡量地区经济发展水平的重要指标,对其进行深入的研究有助于发掘出不同地区的经济发展规律以及导致不同地区GDP出现较大差异的原因。因此,本文基于全国31个省份的GDP数据进行分析,探讨不同省份的经济增长模式,这在一定程度上可以促进各省份之间相互借鉴与学习,改善经济发展不平衡现象。
本文数据来源于Wind数据库,包含全国31个省份从1979—2018年的GDP数据(单位:亿元)。从图1(a)可以看出,随着时间的推移,各省份的GDP的增长越来越快,省份之间的差距不断增大,经济发展不平衡的现象逐渐加剧。为了探讨不同省份的经济增长模式,本文基于各省份每年的GDP增长率((当期GDP-上期GDP)/上期GDP)进行聚类分析。各省份的GDP增长率如图1(b)所示。在宏观经济环境下,各省份的GDP增长率波动趋势相近,但是在部分年份波动幅度又存在着鲜明的不同,适用于本文提出的局部稀疏的函数型K-means聚类。
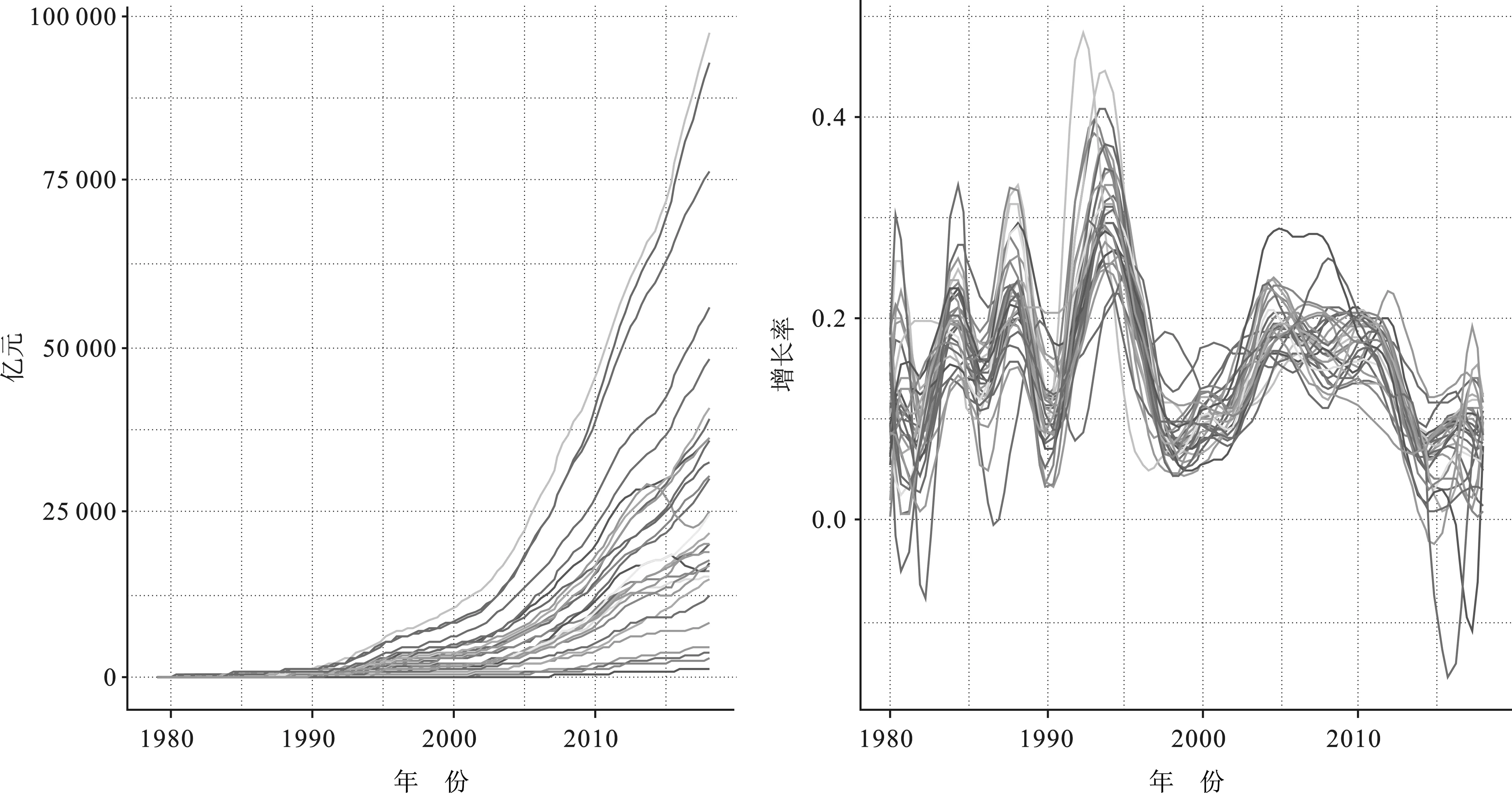
(a)1979—2018年31省份GDP曲线 (b)1979—2018年31省份GDP增长率曲线图1 1979—2018年31个省份的GDP曲线及增长率曲线
接下来对各省份的GDP增长率应用局部稀疏的函数型K-means聚类。在区间T=[1980,2018]上定义18个等距节点,基函数的阶数设置为4阶。聚类数目K的选择采用Jump统计量进行选择[23]。当聚类数目K=5时,Jump统计量最大,因此聚类数目为5类。
聚类的结果如表5所示,将全国31个省份按照不同的经济发展模式分为5类。从表中可以看出,大部分沿海地区的GDP增长速度较快,经济发展迅速,而中西部地区的GDP增长速度较慢。为了进一步分析聚类结果,本文展示了不同类别下的GDP增长率曲线及其均值曲线,如图2所示。第一类省份包含辽宁、吉林等工业大省,第二类省份以西部地区为主。比较第一类和第二类省份的均值曲线,第二类省份的GDP增长率略高于第一类省份,特别是1990年前后和2012年之后。2012年是西部大开发加速发展的初期,在国家政策大力支持引导下,西部地区的经济得到了快速发展。作为传统的工业大省,东北三省的GDP增长速度却较为缓慢。第三类省份包括海南省和江苏省,这两个省份的GDP增长率在1990年前后远远高于其他省份。20世纪90年代初,海南房地产市场开始火热,吸引了来自全国各地的炒房者,海南房价一路飙升,这使得海南经济高速发展,经济增长率达全国第一。随着国家对房地产行业实行了调控政策,房地产泡沫破灭,1995年海南经济增长率跌落至全国倒数。海南的经济因为一时兴起的房地产而高速发展,但没有实现长期的可持续发展。自20世纪90年代以来江苏省大量引入外资,借助地理优势不断扩大开放,发展外向型经济,经济快速发展,1992—1994年实现了连续3年 的高达30%的GDP增长率。第四类省份为浙江省、安徽省、福建省和广东省。借助于改革开放的东风,这四个省份经济增长速度较为相似,在1992—1995年经济发展较快,每年GDP增长率均在20%以上。凭借长期高速的经济发展,江苏省、广东省和浙江省成为了中国GDP的领头省份。第五类省份西藏由于其特殊的历史背景、地理位置和自然气候等原因,GDP增长速度不同于其他省份,被单独划分为一类。图2还展示了函数型稀疏K-means 聚类中各个基函数的权重。从基函数的权重图中可以看出,除倒数第3个基函数,后面11个基函数的权重均为0,这对应着T=[2002,2012]时各类之间无较大差异,在1990年前后存在着显著的差异,这与上述的分析结果一致。

表5 函数型稀疏K-means聚类的结果
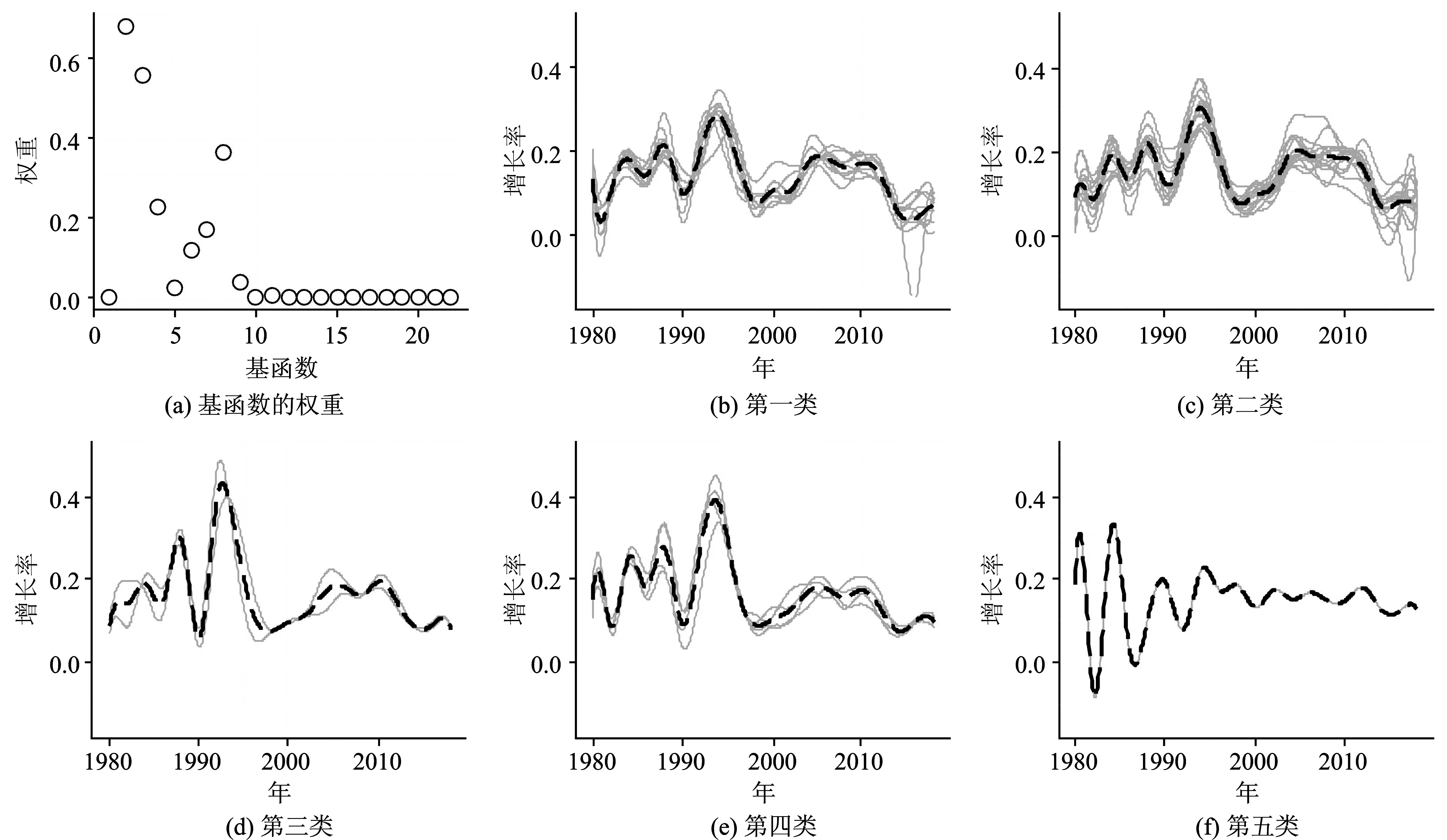
图2 基函数的权重和五类GDP增长率曲线及均值曲线
五、结 论
针对在区间上具有局部稀疏性的函数型数据,本文基于B样条提出了局部稀疏函数型K-means聚类,能同时达到聚类和识别稀疏区间的目的,并将该方法应用于中国31个省份的GDP数据分析中,基于各省份的GDP增长曲线对不同省份的经济增长模式进行聚类分析。
本文的结论有:第一,本文提出的局部稀疏函数型K-means聚类在对函数型数据聚类时考虑了函数区间的局部稀疏性,通过判断与子区间对应基函数的权重是否为零来确定各个子区间是否属于稀疏区间,该方法既能够对函数型数据进行聚类,又能够估计出稀疏区间与非稀疏区间,聚类结果具有很强的可解释性。与现有的SFKmeans相比,本文提出的方法易于理解,普适性更高。第二,根据蒙特卡罗模拟结果,当数据具有局部稀疏结构时,与其他非局部稀疏的方法相比,随着各类曲线重叠比例的增大,局部稀疏函数型K-means聚类的表现逐渐优于其他方法。与SFKmeans相比,本文提出的方法表现不逊于SFKmeans,兰德指数和修正后的兰德指数方差更小。第三,本文将局部稀疏函数型 K-means 聚类应用于中国31个省份的GDP数据分析中,对各省份的经济增长模式进行聚类。本文提出的方法将中国31个省份的经济增长模式聚为五类,各类的经济增长模式在2002—2012年无明显差异,在1990年前后存在着显著的差异。
综上所述,局部稀疏的函数型K-means聚类不仅易于理解,适用范围广泛,而且当数据具有局部稀疏性结构时表现很好,能同时达到聚类和识别稀疏区间的目的,聚类结果的可解释性很强。本文所提出的聚类分析不局限于GDP数据,也可以应用于其他具有局部稀疏结构的函数型数据。

