基于自适应下垂控制的直流微电网多储能SOC动态均衡策略
张 赟, 王 琛, 王 毅,, 韩 冰
(1.华北电力大学 河北省分布式储能与微网重点实验室,河北 保定 071003;2.华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
0 引 言
凭借低线路损耗、高可控性以及无需考虑相位和无功问题等优势,直流微电网成为未来供用电领域的一种重要形式[1-2]。为应对间歇式新能源出力以及负荷功率的随机波动,孤岛运行的直流微电网需增加一定容量的储能以维持系统功率平衡与电压稳定[3]。储能单元通常分布式并联接入直流母线以增大容量配置,然而由于负荷功率分配不合理、初始状态及控制精度差异等因素,多储能间会出现荷电状态(state of charge,SOC)不一致问题,过充或过放都将导致提前退出,继而影响系统的稳定运行[4]。
为解决多储能SOC不一致问题,国内外学者针对多储能功率交互及SOC均衡控制进行了深入研究。文献[5]将储能主导模式划分为6个子模式,考虑各储能单元的过充、过放实现功率交互控制,极限功率限值按照充放电比例分配,使临界单元荷电状态自动恢复至稳定工作区间。文献[6]引入虚拟额定功率概念以实现基于SOC的功率精确共享,但该控制方法需要通信,适用范围具有一定的局限性。此外,依赖下垂控制及其变式作为多储能SOC均衡控制方案已有一定研究。文献[7]将SOC和放电效率作为下垂控制与均衡控制的输入量以补偿系统功率缺额,并采用两段法优化其控制效果。文献[8]利用SOC的非线性对数形式提出了多储能设备SOC一致性控制策略,并通过加速因子实现在线优化。文献[9]在设计直流母线电压与SOC分段下垂关系的基础上,提出了考虑蓄电池SOC的多源协调控制策略。文献[10]设计了下垂系数与socn呈比例关系的SOC均衡方案,使不同储能单元之间功率得到合理分配,但其下垂系数过大或过小均可能会对系统稳定性造成不利影响。文献[11]提出了一种基于SOC的改进下垂控制策略,该策略使得系统抗负载变化能力增强,但其幂指数n仍受到直流母线电压跌落影响。
作为一种在直流系统中被广泛采用的分散控制方法,电压下垂控制可实现多个分布式储能单元之间的自动功率分配[12-13]。为解决SOC不一致问题,目前多数已有研究的核心思想是将SOC值实时引入下垂控制,通过改变下垂系数调节储能功率以达到均衡多储能SOC的目的。然而,这些研究没有考虑下垂系数限值问题,下垂系数随SOC变化时可能会超出允许的范围,进而威胁到系统的安全可靠运行。为了将下垂系数的变化限值考虑在内,本文利用反正切函数将下垂系数与SOC建立联系,从而可保证下垂系数随SOC动态变化时始终处于允许范围。
以含多个分布式储能单元的直流微电网为例,本文对多储能SOC的均衡控制方法展开研究。首先,给出多个储能单元分布式接入直流微电网的结构,并分析其孤岛运行状态。其次,为解决多储能SOC不一致问题同时将下垂系数限值考虑在内,提出一种基于自适应下垂的多储能SOC均衡控制策略,该策略利用反正切函数将下垂系数与SOC建立关联,并引入放大因子以加快SOC均衡速率。此外,对采用所提控制策略的直流微电网进行小信号建模,分析放大因子对系统稳定性的影响。最后,利用RT-LAB实时仿真机等搭建光储直流微电网硬件在环仿真(hardware-in-the-loop simulation,HILS)实验平台,对所提控制策略的有效性进行验证。
1 含多个分布式储能单元的直流微电网
本文研究的直流微电网如图1所示,主要由光伏、风机等新能源发电单元、交直流负荷、多个分布式储能单元以及并网接口构成。直流微电网通过并网接口可与交流大电网相连,此时处于联网状态,也可不与大电网相连,即处于孤岛状态,此时储能单元是系统的功率平衡节点。

图1 含多个分布式储能单元的直流微电网结构Fig.1 Structure of DC microgrid with multiple distributed energy storage units
2 基于自适应下垂的SOC均衡控制
同飞轮、超级电容等新兴储能技术相比,蓄电池具有成本低、技术成熟、应用方便等优势[14]。本文研究的储能单元以蓄电池为例,其荷电状态为剩余容量与总容量的比值,通常以百分数表示,比较常见的估算方法为安时积分法[15],表达式为
(1)
式中:soc0、soc(t)分别为初始t0时刻和当前t时刻蓄电池的荷电状态;CN为额定总容量;iB为充放电电流,处于放电状态时为正;η为充放电效率。
蓄电池的输出功率为
PB=iBuB
(2)
式中:PB在蓄电池放电时为正;uB为端口电压。
蓄电池侧变流器的电压下垂控制表达式为
(3)

2.1 SOC均衡机理
由式(1)、(2)可进一步得到荷电状态估计值
(4)
一般情况下uB变化较小,可看作常数[15],对式(4)两端求导可得
(5)
由式(5)可知,蓄电池放电功率越大,SOC下降速度越快,蓄电池充电功率越小,SOC上升速度越慢。因此,通过控制蓄电池的充放电功率即可实现对SOC变化速率的动态调节。
将式(3)带入式(5)荷电状态变化率进一步表示为
(6)
考虑到udc与uB可视为常数,由式(6)可知,改变下垂控制的参考电压或下垂系数即可调整SOC的变化速率。在放电状态下,荷电状态愈大储能SOC应下降愈快;在充电状态下,荷电状态愈大储能SOC应上升愈慢,以此达到均衡多储能SOC的目的。由于下垂参考电压应尽量控制在额定电压附近,调整范围不大,因此储能荷电状态均衡及其变化速率主要受下垂系数k控制。
2.2 下垂系数对SOC均衡的影响
以两个储能单元为例分析下垂系数对SOC均衡的影响,电压下垂控制表达式分别为
(7)
由于直流微电网的物理尺度较小,且分布式储能单元多并联在同一直流母线,可近似认为udc1≈udc2,根据式(7)可得
(8)
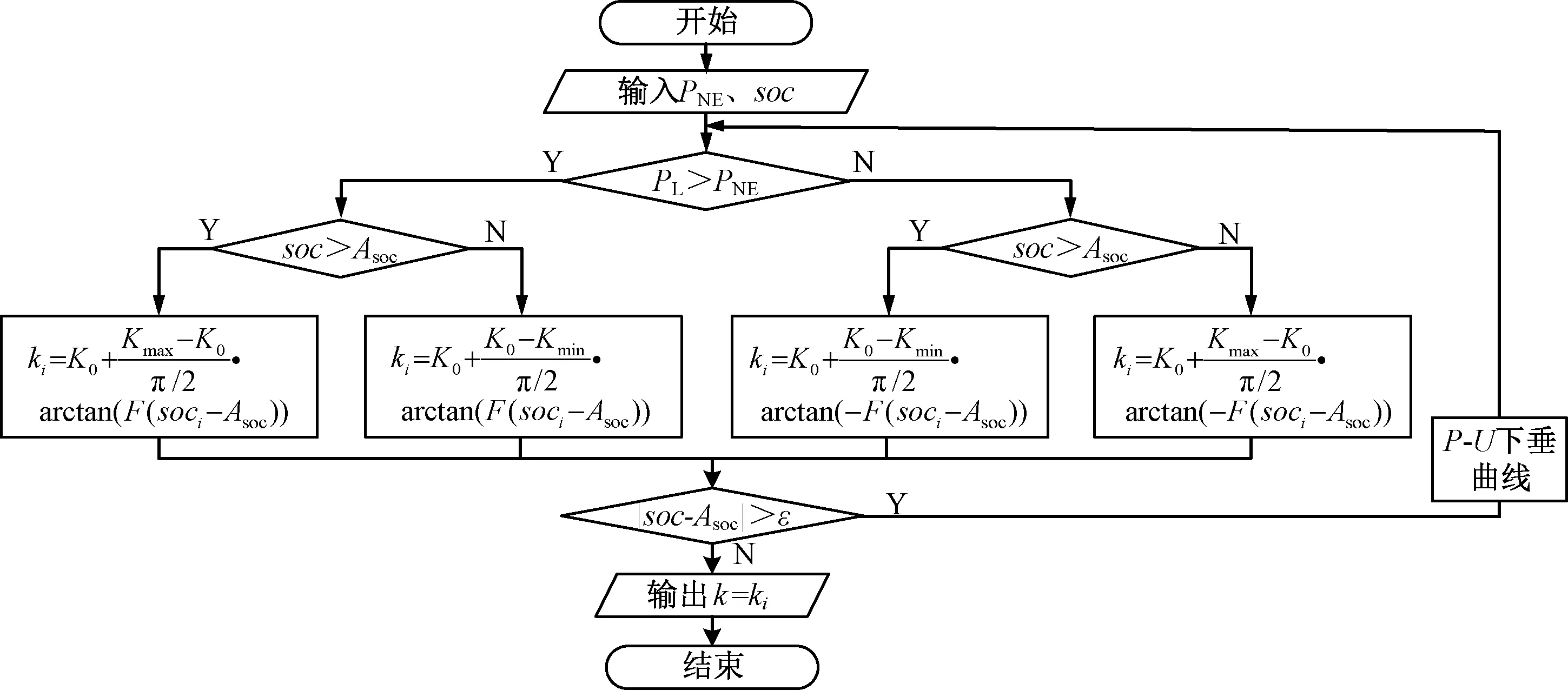
为了实现多储能SOC的均衡,储能单元承担的功率应根据荷电状态进行合理分配。当储能单元处于放电状态时,SOC较大的储能单元应输出功率较多,SOC较小的储能单元应输出功率较少;反之,当储能单元处于充电状态时,SOC较大的储能单元应吸收功率较少,SOC较小的储能单元应吸收功率较多。以soc1>soc2为例,放电状态下,P1应大于P2,故应使k1>k2;充电状态下,|P1|应小于|P2|,故应使k1 以上分析进一步验证了储能SOC的上升、下降速度与充电、放电功率大小有关,即与下垂系数有关。提高SOC均衡速度则应尽量增大储能单元下垂系数之间的差值。为了将下垂系数的变化范围考虑在内,并提高储能SOC的均衡速度,本文采用反正切函数建立下垂系数与SOC的关联。 由于储能SOC数值较小(0~1之间)且变化缓慢,本文引入放大因子F以进一步放大多储能SOC之间的差异。根据上述分析,当储能单元处于放电状态时,自适应下垂系数k设计为 (9) 式中:K0为初始下垂系数;Kmin、Kmax分别为允许的最小、最大下垂系数;Asoc为n个储能单元荷电状态的平均值,即Asoc=(soc1+…+socn)/n。通过调整放大因子F可控制多储能SOC的均衡速度。 当储能单元处于充电状态时,自适应下垂系数k设计为 (10) 以储能放电状态为例,式(9)表示的自适应下垂系数的变化曲线如图2所示,反正切函数的自身特性可使下垂系数始终保持在限值Kmin与Kmax之间,Kmin、Kmax可根据系统对直流电压的要求以及稳定性分析等因素确定。从图2可以看出,随着SOC不平衡程度的变化,下垂系数在允许的范围内自适应变化,在SOC均衡过程中下垂系数逐渐趋近于初始下垂系数K0。此外,不同储能单元SOC差异愈大,对应变流器控制中的下垂系数愈趋近于限值Kmin或Kmax,有利于增大不同储能单元之间分配功率的差距,进而加快多储能SOC的均衡速度。 图2 放电状态下自适应下垂系数变化曲线Fig.2 Variation curve of adaptive droop coefficient on discharged state 本文所提多储能SOC均衡控制策略的控制流程如图3所示,图中PL为负荷功率,PNE为新能源发电功率。根据系统源、荷功率的大小可判定储能的充放电状态,再通过比较单个储能SOC与系统SOC平均值即可确定每个储能自适应下垂系数的取值。考虑到实际监测中存在误差,当|soc-Asoc|小于误差因子ε时,即认为各soc相等,即各储能单元荷电状态达到均衡。 图3 多储能SOC均衡控制策略流程图Fig.3 Flow chart of the SOC balancing control strategy for multiple energy storage units 通过调节放大因子可以控制多储能SOC的均衡速度,为了给放大因子的取值提供参考,并研究放大因子对系统稳定性及动态特性的影响,接下来对所提控制策略进行稳定性分析。 以包含光伏、两端蓄电池以及负荷的直流微电网为研究对象,如图4所示,其中光伏运行在最大功率跟踪状态,交流负荷为恒功率型负荷,蓄电池作为系统平衡节点维持直流母线电压的稳定。PPV、PL、PB1、PB2分别表示光伏功率、负荷功率以及两端蓄电池功率,其中PB1、PB2以流向直流母线为正。蓄电池变流器B-DC1、B-DC2采用本文所提基于自适应下垂的多储能SOC均衡控制策略。 图4 光储直流微电网Fig.4 PV-battery-based DC microgrid (1)蓄电池变流器小信号建模 以放电状态为例,且假定蓄电池1的SOC较大,则B-DC1、B-DC2的自适应下垂系数为 (11) 图5为蓄电池变流器的小信号控制框图,其中GP、GI是PI控制器的比例系数和积分系数,D为占空比。 图5 蓄电池变流器小信号控制框图Fig.5 Small signal control block diagram of battery converter 根据蓄电池变流器的数学模型以及小信号分析框图,可得如下微分方程组 (12) 式中:LB为变流器的电感值;DP、DI分别表示占空比的比例和积分部分。这里将蓄电池看作理想电压源,UB取为常数。 将式(11)带入式(12),并在初始稳态值附近线性化,可得蓄电池变流器的小信号模型 (13) 式中:Δx=[ΔiB, ΔDI]T,Δy=[Δudc, Δsoc1];系数矩阵AB、BB见附录。 (2)微电网小信号建模 为简化分析,将光伏、负荷设为恒定功率源。各端经变流器连接至公共直流母线,并忽略线路阻抗,如图6所示。 图6 直流微电网简化电流关系图Fig.6 Simplified current relationship diagram of DC microgrid 根据KCL,可得关于直流母线电压的微分方程 (14) 式中:Cdc为直流母线电容;idc_PV、idc_B1、idc_B2、idc_L代表各端直流侧电流,各端电流可表示为 (15) 设蓄电池充放电效率为常数,由式(6)可得 (16) 联立式(14)、(16)并在初始稳态值附近线性化可得 (17) 式中:系数矩阵CB、DB见附录。结合式(13)、(17),可得直流微电网小信号模型为 (18) 式中:ΔxB=[Δx,Δy]T;系数矩阵Asys见附录。 根据式(18)可绘制放大因子变化时直流微电网系统的特征根轨迹,根据特征根轨迹结果,该系统共有四个特征根,图7显示了主导特征根的变化轨迹,其中放大因子F以10为步长,从10增大到1 000,其变化趋势为图中箭头所指方向。另外两个特征根是远离虚轴且变化范围较小的负实根,对系统稳定性影响不大,此处不作分析。 图7 放大因子变化时的特征根轨迹图Fig.7 Characteristic root locus diagram when magnification factor changes 观察图7可知,主导特征根s1、s2始终处于左半平面内,随着F的增大,该共轭复根按图中箭头所指趋势先向远离实轴的方向移动,再逐步靠近实轴,此过程系统处于欠阻尼状态,有一定的超调量,系统振荡先增大后减小;当放大因子F继续增大,s1、s2变为移动方向相反的负实根,系统处于过阻尼状态,且s1沿实轴逐步靠近零点方向,稳定裕度降低,所以放大因子不宜过大。综上,在选择放大因子时,应保证系统在多储能SOC达到快速均衡的同时兼具一定的动态性能与稳定裕度。 为验证所提多储能SOC均衡控制策略的有效性,本文搭建了包含两端蓄电池的光储直流微电网HILS实验平台,如图8所示。该HILS实验平台由RT-LAB实时仿真机、DSP控制器以及上位机PC等构成,本文所提与B-DC相关的控制策略部署在实际DSP中,实时仿真模型通过上位机下载到RT-LAB中。DSP产生的PWM脉冲经光电隔离模块传送至RT-LAB的脉冲输入端口,实验波形可通过RT-LAB前面板的min-BNC接口连接至示波记录仪上进行记录。直流微电网实时仿真模型与图4一致,相关参数见附录表1,本文取Kmin、Kmax分别为10和100。接下来对所提控制策略进行测试,测试结果中的PB1、PB2以流入直流母线为正。 图8 光储直流微电网HILS实验平台Fig.8 Experimental HILS platform of the PV-battery-based DC microgrid 蓄电池处于放电状态时的测试结果如图9所示,这里放大因子F取值为100。测试开始时,负荷功率为30 kW,光伏发电功率为10 kW,两个蓄电池的荷电状态soc1、soc2分别约为70%、68%,B-DC1、B-DC2采用常规下垂控制,放电功率PB1、PB2约为10 kW。第5 s时,B-DC1、B-DC2采用的控制策略切换为所提基于自适应下垂的SOC均衡控制策略,B-DC1的下垂系数k1由50增大至约75,放电功率PB1由10 kW增大至约14.5 kW,soc1下降速度加快;B-DC2的下垂系数k2由50减小至约30,放电功率PB2由10 kW减小至约5.5 kW,soc2的下降速度减缓。k1、k2随SOC变化时始终处于Kmin与Kmax之间,且随着soc1和soc2差异的减小而逐渐趋近于初始值。约22 s时,soc1、soc2与平均值之间的差值小于误差因子ε,即可认为soc1、soc2相等,k1、k2恢复至初始值50,PB1、PB2也随之相等,测试结果与理论分析一致。 图9 放电状态测试结果(F=100) Fig.9 Test results on discharged state (F=100) 蓄电池处于充电状态时的测试结果如图10所示,这里放大因子取值为100。测试开始时,负荷功率为10 kW,光伏发电功率为30 kW,两个蓄电池的荷电状态soc1、soc2分别约为70%、68%,B-DC1、B-DC2采用常规下垂控制,充电功率PB1、PB2约为10 kW。第5 s时,B-DC采用的控制策略由常规下垂控制切换至所提控制策路,下垂系数k1由50减小至约32,充电功率PB1由10 kW减小至约6 kW,soc1上升速度减缓;下垂系数k2由50增大至约76,充电功率PB2由10 kW增大至约14 kW,soc2的上升速度加快。约83 s时,soc1和soc2达到均衡状态。 图10 充电状态测试结果(F=100) Fig.10 Test results on charged state (F=100) 图9与图10的测试结果说明,在所提控制策略下,储能变流器的下垂系数随SOC在允许范围内变化,从而合理分配储能之间的充放电功率,SOC大的储能放电速度加快、充电速度减慢,SOC小的储能放电速度减慢、充电速度加快,因此可实现多储能SOC之间的动态均衡。 为验证所提控制策略中放大因子对SOC均衡速度的影响,图11给出了蓄电池处于放电状态时放大因子F取值为500的测试结果,测试初始条件与图9一致。在第5 s采用所提控制策略后,k1由50增大至约94,PB1由10 kW增大至约17.2 kW,k2由50减小至约15,PB2由10 kW减小至约2.8 kW,约13 s时,soc1、soc2即已达到均衡。与图9所示的测试结果相比,增大放大因子后,soc1的下降速度进一步加快,soc2的下降速度进一步减缓,soc1、soc2的均衡速度明显加快。因此,在满足系统稳定性的前提下,通过调节放大因子可对多储能SOC的均衡速度进行控制。 图11 放电状态测试结果(F=500) Fig.11 Test results on discharged state (F=500) (1)针对含多个分布式储能的直流微电网,本文提出了一种基于自适应下垂控制的多储能SOC动态均衡策略,该策略利用反正切函数使下垂系数与SOC建立联系,可保证下垂系数在允许范围内自适应地随SOC变化,进而实现多储能SOC的动态均衡。 (2)利用小信号建模分析了放大因子对系统稳定性的影响,通过调节放大因子可对多储能SOC均衡速度进行控制,合适的放大因子可在快速均衡多储能SOC的同时使得系统具备良好的动态性能。 (3)搭建的光储直流微电网HILS实验平台充分验证了所提控制策略的有效性,所提控制策略对于交流系统中多储能单元的SOC均衡问题亦具有一定的参考价值。2.3 自适应下垂系数设计

3 控制参数稳定性分析
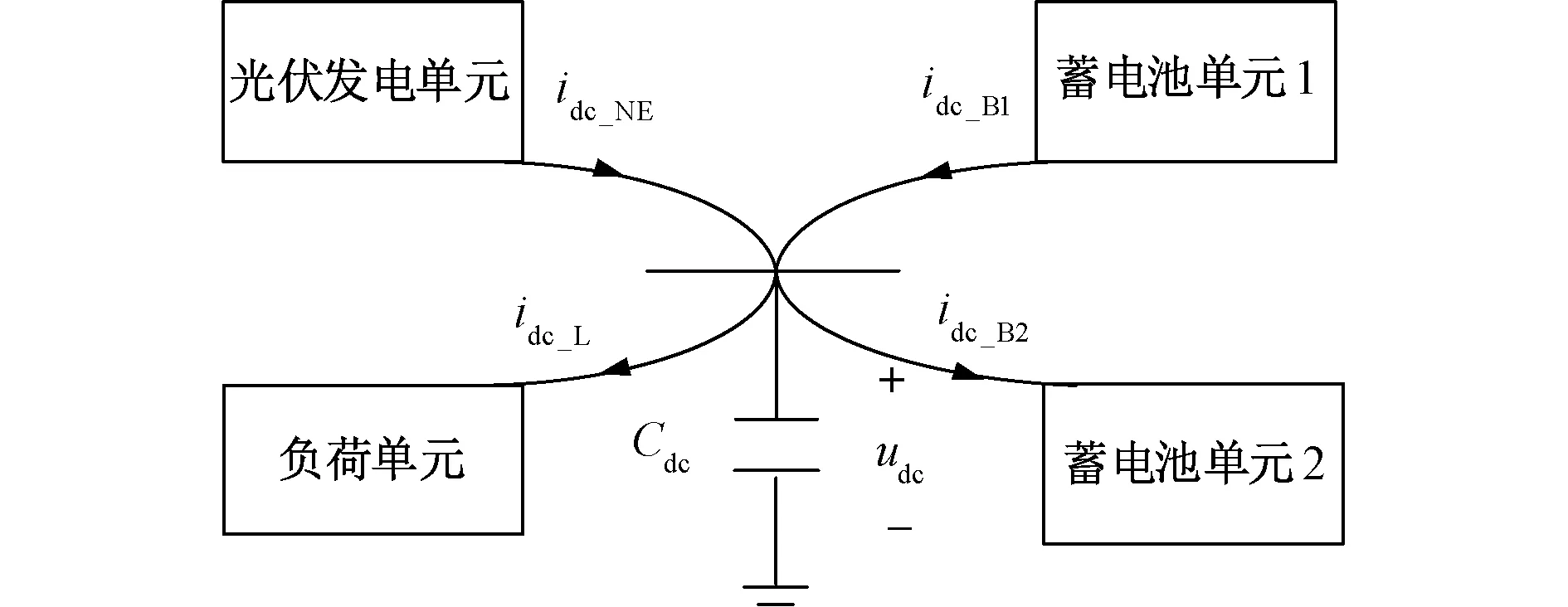
3.1 直流微电网小信号建模


3.2 稳定性分析

4 实验验证

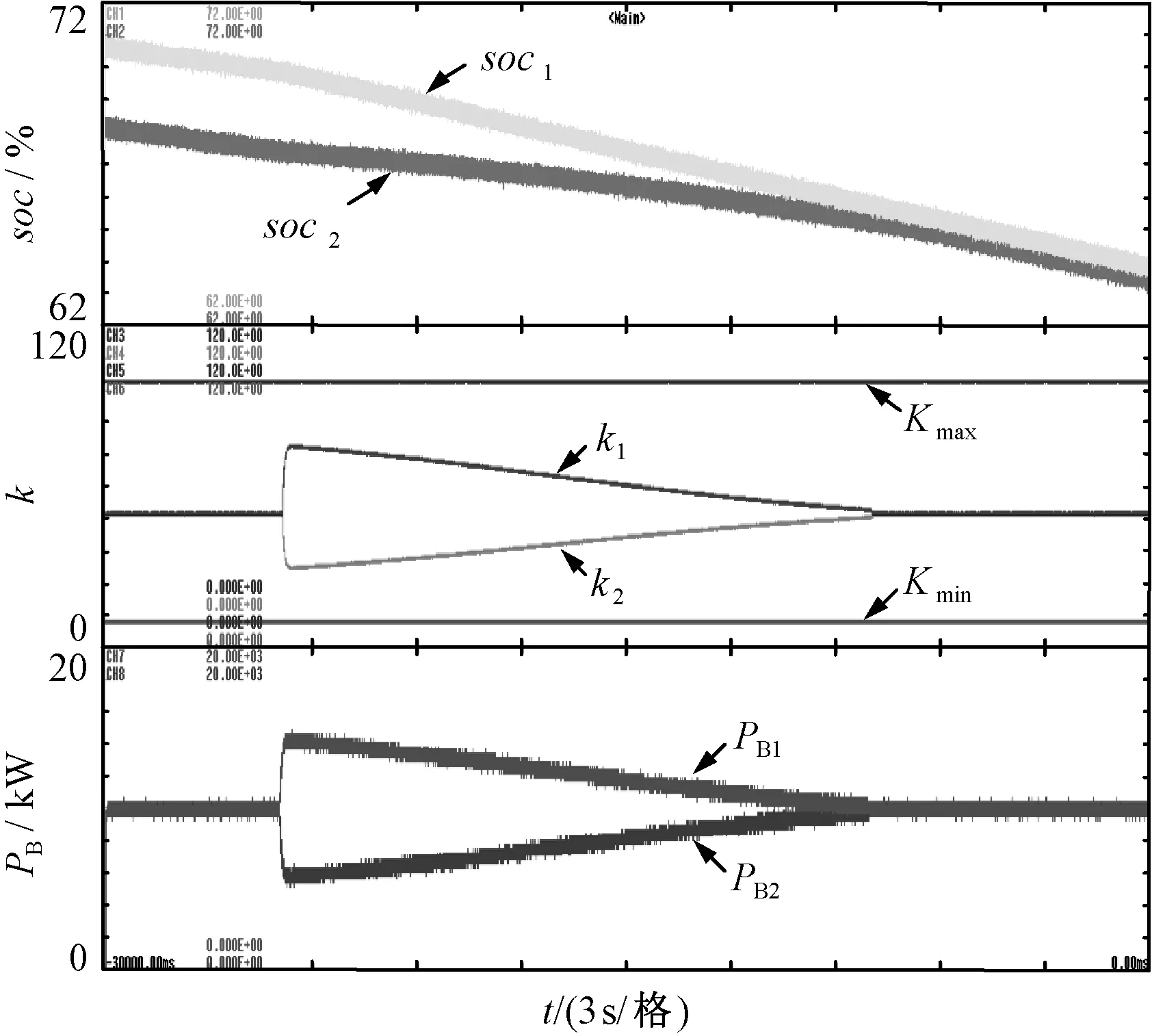
4.1 放电状态测试
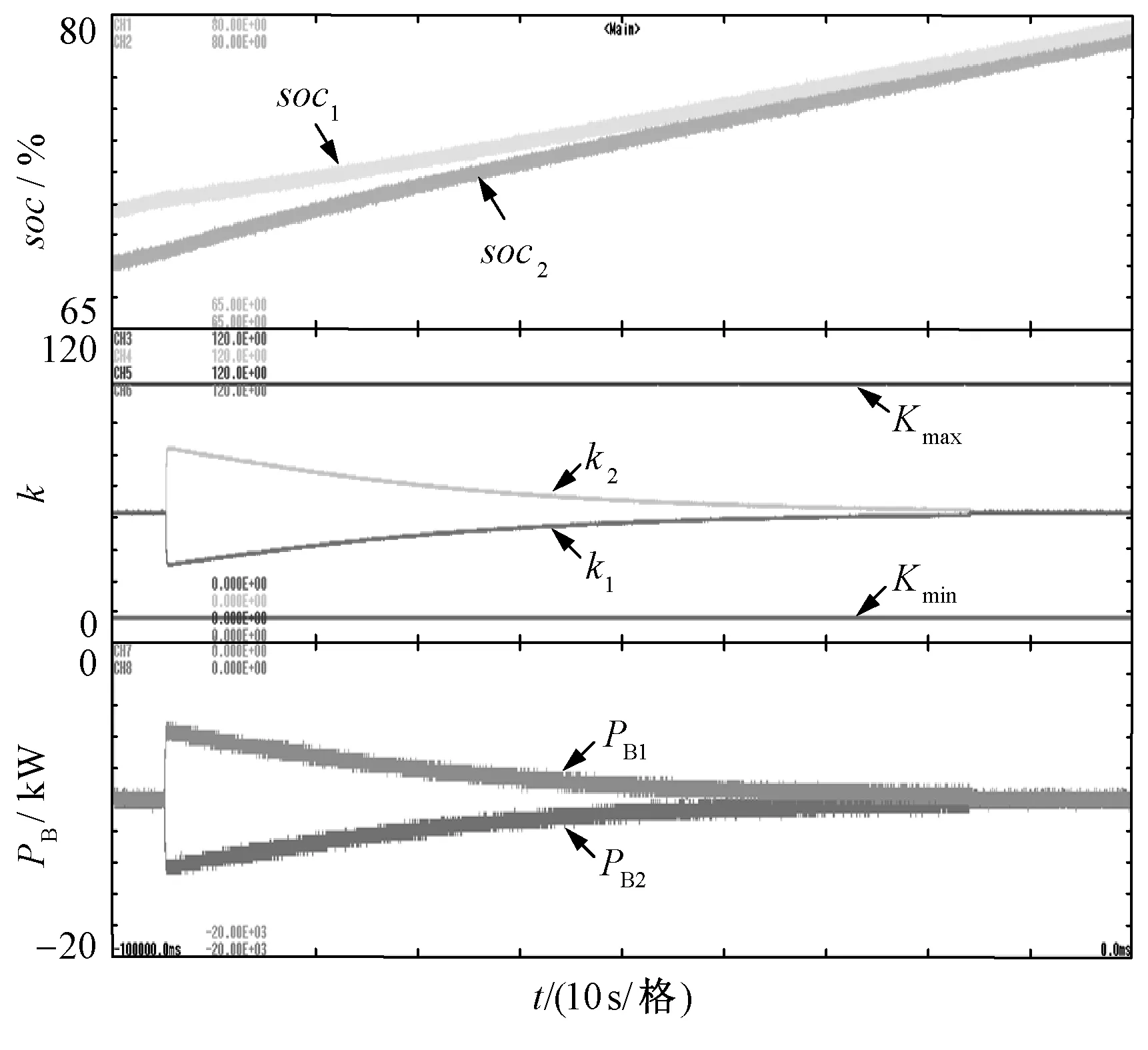
4.2 充电状态测试
4.3 SOC均衡速度测试

5 结 论

