基于最小二乘支持向量机的变压器故障诊断研究

高 洁，席先鹏

(1. 湖北宣恩洞坪水电有限责任公司，湖北 宣恩 445000；2. 国网利川市供电公司，湖北 利川 445400)

油侵式变压器是电力系统中的枢纽设备，是电力系统能否安全、有效运行的关键因数之一。长期运行之后变压器会出现一系列的故障，有显形的也有隐形的，显形故障容易发现而隐形故障不容易发现。因此能否快速、准确地检测出隐形故障对变压器的使用寿命以及安全运行有重大的意义。变压器非正常运行时，油中会产生许多故障气体，所以DGA技术应运而生。Disssolve Gasses Analysis(油中溶解气体分析)技术[1]是早期的故障诊断技术，也是十分重要的方法，对变压器故障诊断的发展具有重大意义。但由于DGA技术的故障编码不完全和编码界限模糊等原因，DGA法对变压器的诊断结果不是很准确，而且对于多重故障也无能为力。

经过专家学者多年研究，在DGA基础上提出了一系列人工智能算法。如：BP神经网络算法[2]、遗传算法等[1]。BP神经网络容易陷入局部最优而且收敛速度慢。遗传算法准确率相对BP神经网络有所提高但速度太慢。

Support Vector Machine(支持向量机)是一种新的学习模型，它主要用于问题的分类和回归分析。本文用于非线性分类，主要思想就是把低维不可分样本转换到高维空间中使其线性可分。Least Squares-Support Vector Machine采用松弛变量的平方作为修正量，将二次规划求解转化为求解线性方程组，不但增加了求解速度而且计算难易度也减小了。

本文以DGA气体数据为基础，采用LS-SVM对油侵式变压器进行故障诊断。

1 LS-SVM算法[3-5]

假设样本集P={xi,yi}(i=1,2,…,n)，xi是输入矢量；yi是输出矢量；n是样本总数。选择一个非线性映射Φ(x)将xi转换到高维的空间Γ(其中xi∈Rd，yi∈R)，在高维空间Γ下构造最优线性决策函数：

f(x)=sgn(ωφ(x)+b)

(1)

式中：ω是权值向量；b是误差常数。

在建立决策函数时，根据结构风险最小化原则找到ω和b就是最小化[6-7]：

J=‖ω‖2/2+C·Remp

(2)

式中：‖ω‖为控制模型的复杂度；C为惩罚因子；Remp为误差控制函数，也就是ξ不敏感损失函数。

选择不同的不敏感损失函数(Huber损失函数、线性ξ损失函数、二次ξ损失函数)可以建立不同类型的SVM。

而LS-SVM用ξ的二次方作为损失函数，所以优化目标为：

(3)

通过求解Largrange函数的鞍点[6-7]得到：

(4)

式中：a为拉格朗日乘子，根据库恩-塔克条件[8](∂L/∂ω=0，∂L/∂b=0，∂L/∂ξ=0，∂L/∂a=0)求导得：

(5)

由式(5)可得：

(6)

式中：Z=[φ(x1)Ty1,…,φ(xn)Tyn]，Y=[y1,…,yn]，L=[1,…,n]，ξ=[ξ1,…,ξn]。

式(6)消去ω和ξ可得：

(7)

式中：Ω=[φ(xk)T]Tφ(xi)，Y=[y1,…,yn]T，M=[1,…,n]T，ξ=[ξ1,…,ξn]，a=[a1,…,ai]。

对式(7)用最小二乘法求出a和b，得到分类决策函数[9]为：

(8)

式中，K(x,xi)为核函数。

2 和声搜索优化算法

和声搜索算法(Harmony search，HS)是一种新颖的智能算法，可以对不同测试方式进行优化处理，其原理为反复调整、选择及验证记忆库中的解变量，不断进行迭代运行，最终使函数值逐渐收敛，从而完成目标方法的优化。

2.1 和声搜索算法流程图

和声搜索算法流程见图1。

图1 和声搜索算法流程图

2.2 参数优化步骤

1)初始化各个参数：音高调整率PAR、记忆库大小HMS、和声记忆库保留率HMCR、算法终止条件(最大迭代次数)、变量数目、各个变量取值范围。

2)从各个变量的取值范围内随机选取步骤(1)中规定数目的解向量，并按照目标函数(式(8))值的正确率排序。

3)根据HMS、HMCR、PAR生成一个新的和声，具体如下：①在HMCR概率下各个变量取值来源于HM；②在1-HMCR概率下各个变量取值来源于非HM的值域其他值；③在a条件下有PAR概率对选取的变量进行微调，微调公式如下：

(9)

式中：bw为固定带宽；rand(-1,1)是-1到1之间的随机值。

重复上面的工作，直到达到最大的迭代次数，最后，从HMS中选取最小的那个解向量相应的f(x)，f(x)就是相应的最小值。

3 变压器故障诊断

3.1 样本气体选取

样本气体选取H2、CH4、C2H6、C2H4、C2H2五种故障气体作为输入。选取高温过热、高能放电、中温过热、正常、低温过热、低能放电、局部放电七种故障状态作为输出(见表1)。

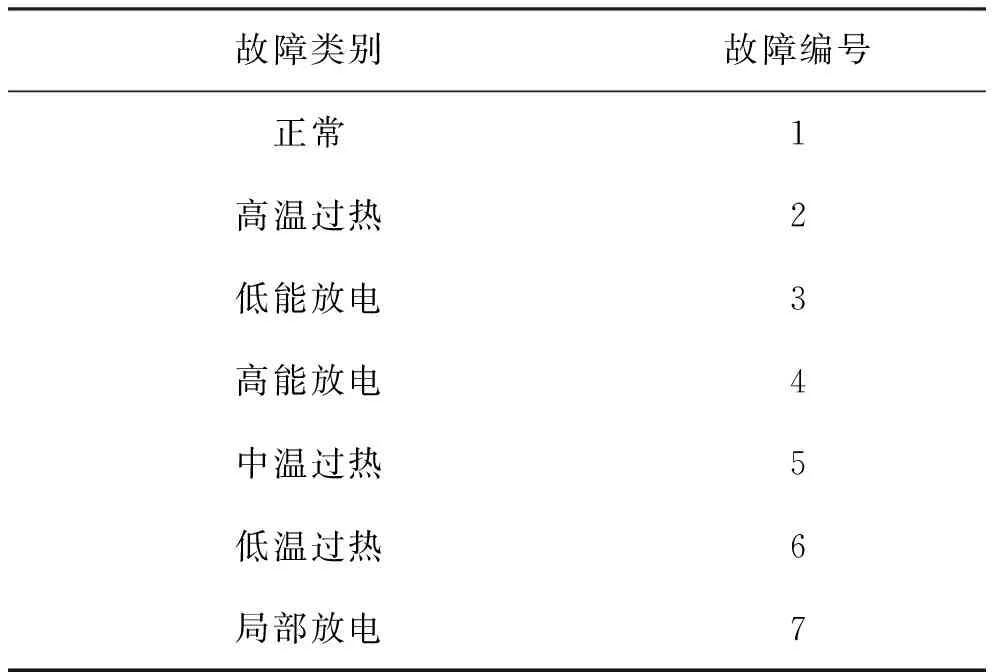
表1 故障的对应编码表

3.2 数据的归一化处理

油中的故障气体含量不可能都相差不大，有的数据可能相差比较大，如果不做处理代入程序中诊断误差可能非常大，如图2。因此，将样本数据根据以下公式进行转变，尽可能减小仿真误差。

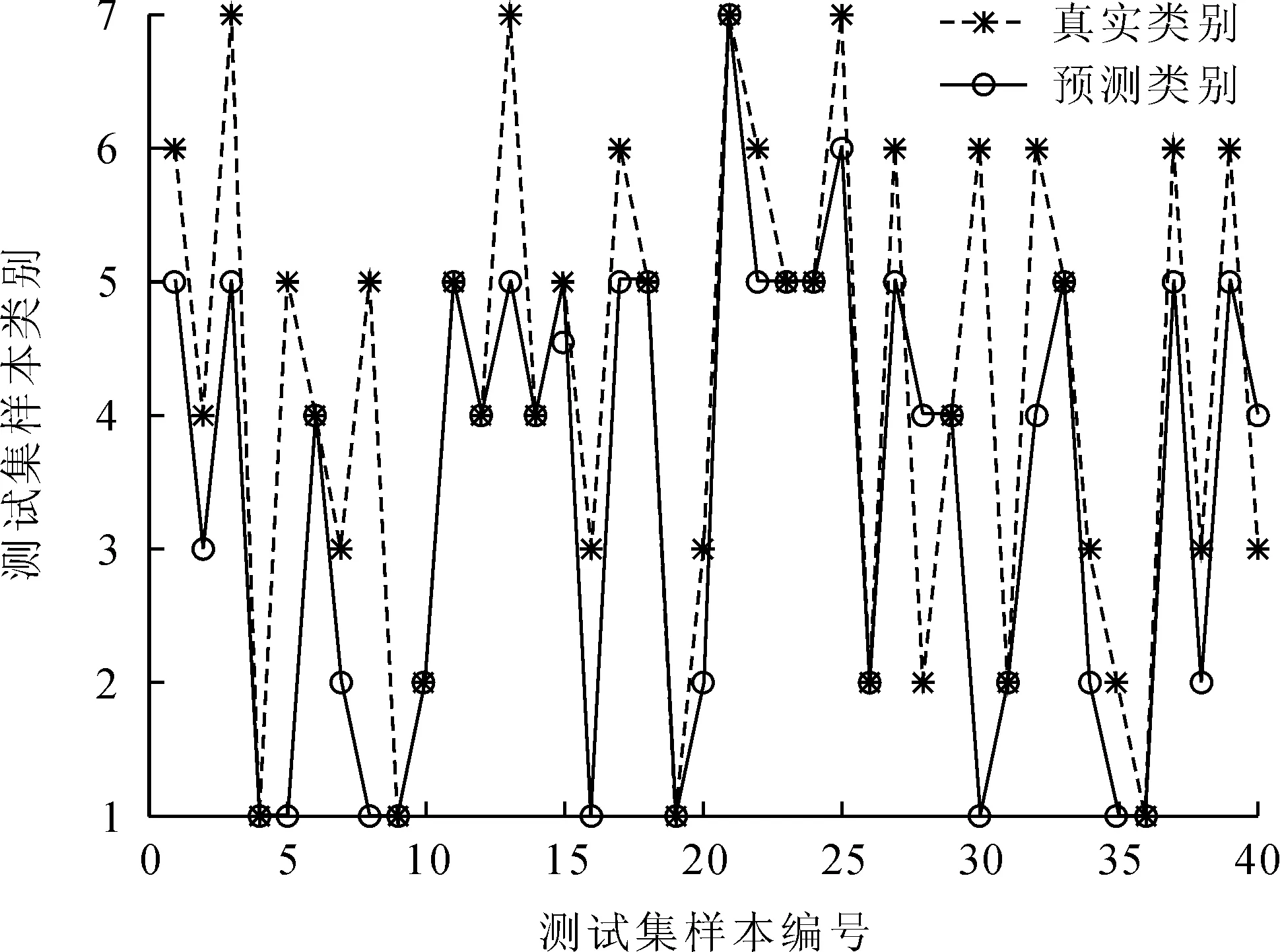
图2 无归一化诊断结果图

(10)

式中，ai为一种气体的体积。

3.3 核函数选取

目前，应用较多的核函数有：

1)d阶多项式核函数[9-10]

K(x,xi)=(xxi+1)d

(11)

2)Sigmoid核函数[10]

K(x,xi)=tanh(k(xxi)+θ)

(12)

3)径向基核函数(RBF)[11]

(13)

本文选用径向基核函数，因为RBF只有一个参数需要优化而且将数值限制在0和1之间。

3.4 诊断结果

本文选用160组样本数据进行故障仿真。其中训练样本120组，测试样本40组。由仿真测试结果表明优化后的LS-SVM诊断结果更准确(见图3、图4及表2)。

图3 未优化的LS-SVM预测结果图

图4 优化后的LS-SVM预测结果表

表2 无归一化、未优化、优化测试准确率对比表

由杨春玲等[11]的方法对比得知，本文利用和声搜索算法对LS-SVM算法进行优化，如表3所示相较于三比值法、ELMAN神经网络法及多层动态自适应优化参数法，具有较高准确性。

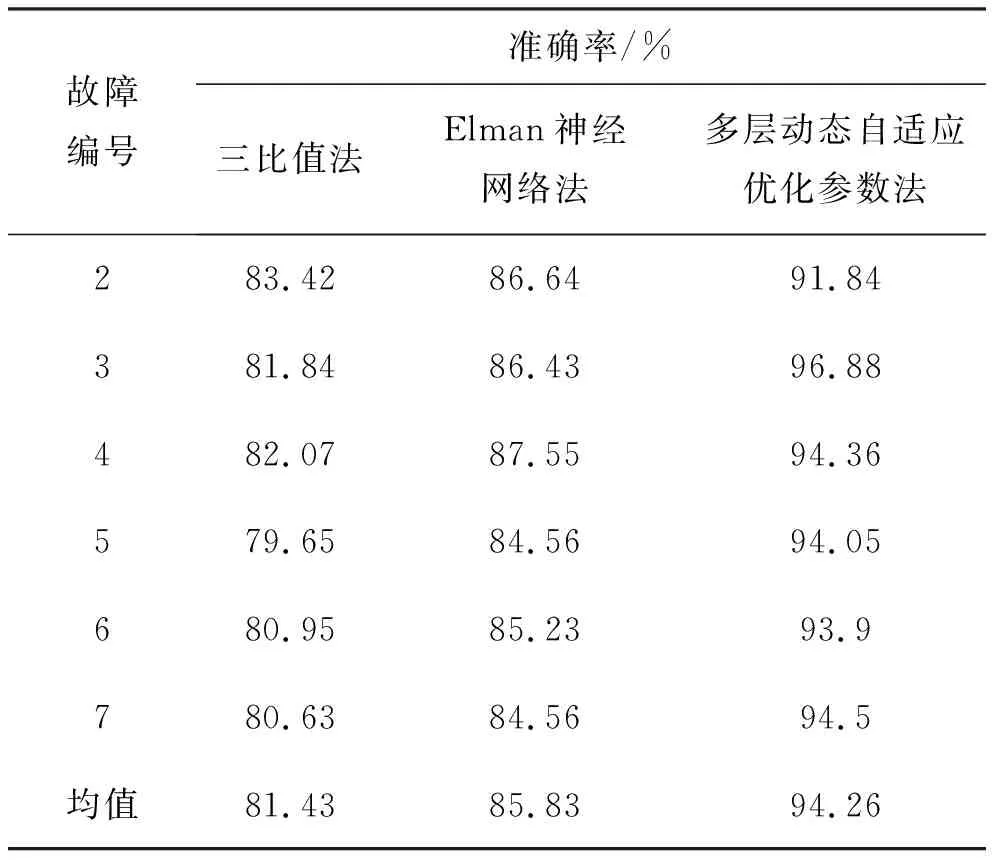
表3 三比值法、Elman神经网络法、多层动态自适应优化参数法准确率对比表

4 结 语

在LS-SVM算法基础上提出了用和声搜索算法对LS-SVM中的核函数参数和惩罚因子进行优化处理。和声搜索算法通过不断迭代运行，以寻找与目标值贴合的测试数据，能够较为准确的将所需解值定位。本文结果与其他方法进行对比分析，表现出结果数据的优化效果较为明显，在有限组样本条件下，一定程度上提高了LS-SVM算法的诊断准确度。