分布式驱动舰载机无杆式牵引车的驱动防滑

戚基艳，金嘉琦,付景顺

(沈阳工业大学 机械工程学院， 沈阳 110870)

无杆式舰载机牵引车能够更好地融合先进设计技术，操纵稳定性、灵活性更高，作为舰基保障的一种新型设备，在现代舰载机调运中广泛使用[1]，影响着舰载机的调运安全与效率[2-3]。舰载机的调运作业在很大程度上影响着舰载机的起降[4]，直接影响着航空母舰战斗力的发挥[5]，因此保证牵引车在狭窄拥挤的舰船甲板上行驶的稳定性至关重要。由于海浪运动带来的舰船摇摆运动，给舰载机牵引车的行驶带来了更多的不确定性因素。近年来，甲板作业自动化、智能化等一系列问题已经成为当前的研究热点[5-7]。

目前对于舰载机被稳定牵引地研究主要是基于一定算法进行的路径跟踪规划，从而保证运行工况的高效和稳定性[2-3,6]。研究背景大多是陆地环境，没有考虑复杂的舰载情况[7]。国外的研究主要集中在结构设计和产品研发上，对于行驶运动特性地研究比较少[8]。本文研究的一款遥控舰载机无杆式牵引车，在动力性能和结构方面具备明显优势[8-9]，研究其在舰船上行驶的驱动防滑控制策略。目标牵引车由轮毂电机驱动，具有驱动链短、传动效率高、转矩控制自由度和精确度高等诸多优点，非常适合控制受舰船运动影响的舰载机牵引车的复杂运行工况。驱动防滑作为车辆重要的主动安全技术之一[10]，能够通过实时调整轮毂电机的输出扭矩，使车辆在复杂的运行工况下保证加速过程的快速而稳定。

针对轮毂电机驱动的车辆驱动防滑控制算法主要集中在基于滑转率控制和基于电机输出转矩控制两种。其中基于滑转率控制算法不仅需要对车速和路面进行实时识别，而且需要辨识最优滑转率，实时、精确辨识这些参数是控制的难点[10]。舰载机无杆式牵引车主要运行在单一的舰船甲板面，也就是路面条件单一，但是对于甲板面附着条件相关文献研究较少。考虑到以上分析的原因，本文拟通过在不事先假定最优滑转率，也不估计舰面附着系数的情况下，通过在线自动寻找到最优的滑转率，通过控制轮毂电机的输出转矩，从而使轮胎力达到可利用的最大值，实现舰载机牵引车驱动防滑控制的目的。

1 舰载机无杆式牵引车系统

1.1 系统坐标与舰船运动

建立的系统动力学模型如图1所示[8]。On-xnynzn是惯性坐标系，质心是海平面某一点；Oj-xjyjzj是船体质心坐标系，坐标原点是舰船质心；Oi-xiyizi(i=1，2)为牵引车和舰载机的连体坐标系，坐标系原点是质心。坐标变换按照航向—纵摇—横摇的顺序[11-12]。

假设船体相对于质心运动，可将船体运动与欧拉角结合[13-14]，简化表示为:

ls=lo(ωPt+AP) (l=α、β、γ;p=1、2、3)

(1)

式中：ls(αs、βs、γs)分别为舰船的横摇、纵摇和垂荡运动规律，l0(α0、β0、γ0)分别为舰船的横摇、纵摇和垂荡的运动幅值；ωp(ω1、ω2、ω3)表示舰船遭遇频率；Ap(A1A2A3)表示初始相位角。

1.2 舰载机无杆式牵引车系统模型

根据文献对舰载机无杆式牵引车的纵向动力学分析[9]，假设舰船坐标系为平动非惯性系，目标牵引车由两后轮进行驱动，其运动学方程可以表示为：

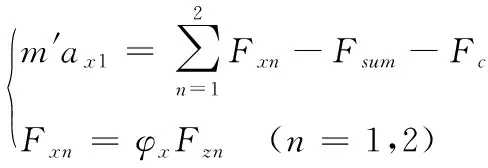
(2)

其中：

(3)

式中：m为舰载机无杆式牵引车的等效质量：结构设计时将舰载机作用于牵引车的重力作用点与两后驱动轮轴线中心点重合[15]，牵引车后轴大约承担10%的舰载机质量[16]；ax1是牵引车在舰船坐标系下的纵向行驶加速度，ax2是舰船在惯性坐标系下的纵向行驶加速度，舰船属于平动非惯性系。Fc是舰船提供的惯性力；Fsum牵引车行驶时所受的阻力之和；其中Ff1是牵引车所受的滚动阻力，Fw1是牵引车所受的空气阻力；Fgx1是牵引车自身重力的分力，Fqx1是假设舰载机与牵引车纵向速度和相对舰船夹角相等的情况下，舰载机所需的纵向牵引力，即牵引车提供给舰载机的力。Fxn是两后驱动轮的垂向载荷：n=1，2，代表两后驱动轮的轮胎序列号，后续文章n的代表意义相同；φx是甲板面附着系数，与普通汽车行驶工况不同，舰载机无杆式牵引车的行驶路面即舰船甲板面路况比较单一，附着系数相对固定，可以用双线性模型[17]简化表示牵引车纵向附着系数：

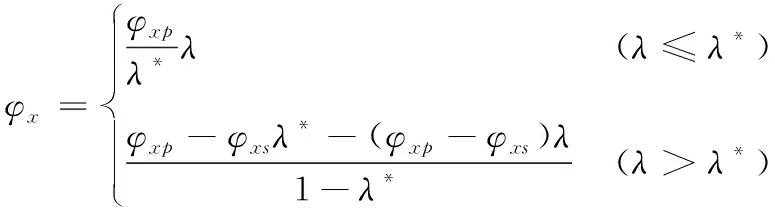
(4)

其中：

(5)

式中：φxp为甲板面峰值附着系数；φxs为甲板面滑动附着系数；λ*为甲板面峰值附着系数对应的最优滑转率；λ为牵引车的滑转率；rd为牵引车的车轮半径；vx1为牵引车的车身速度。

1.3 车轮运动学模型

将牵引车作为刚体质点系来考率，忽略牵引车行驶过程中的俯仰与侧倾，仅研究牵引车的纵向运动，轮毂电机驱动能够独立控制，故驱动轮的受力分析可采用单轮驱动模型，在牵引车自身坐标系下，可知目标牵引车的驱动轮的动力学方程为：

(6)

式中：Ttn是轮毂电机提供的驱动力矩；rd是车轮半径。

若不考虑牵引车旋转质量惯性阻力偶矩和滚动阻力偶矩，且牵引车行驶速度较慢，可以不考虑空气升力的影响。则牵引车两后驱动轮在连体坐标系下的垂向载荷可以表示为：

(6)

式中：d为牵引车两后轮的轮距；ay1是牵引车加速行驶时在舰船坐标系下的侧向加速度；l1是牵引车前轴距质心的距离；L是牵引车的轴距；hjc是牵引车质心距舰船质心的距离。

2 控制策略

针对分布式驱动汽车的牵引力驱动防滑控制，目前主要有3种方法，第1种是通过实时的滑转率跟随已知的最优目标滑转率的间接控制技术，由于汽车行驶路况的不同，最优滑转率的数值一直在变，固定的一个最优值很难实现多工况下的驱动力最优。第2种是通过提前预估路面的附着系数，从而根据附着系数控制滑转率，由于传感器的精确度和其标定、安装等因素限制，且紧急情况时，路面附着系数预估很难在短时间内精确完成，因此该种方法目前在汽车上还处于理论研究阶段，有诸多需改进的空间[10]；第3种则是在附着系数和最优滑转率均未知的情况下，在线寻找最优滑转率。舰载机无杆式牵引车主要在舰船的甲板上移动，指定舰船的舰面附着系数比较单一，但不同舰船的舰面附着系数由于制造工艺不同，又存在一定的差异性。目前对舰面附着系数的相关研究文献较少，最优滑转率和附着系数相关研究数据缺乏，大多集中在舰船甲板面的防滑摩擦因数的研究[18]。基于以上分析，考虑到复杂拥挤的舰面条件以及海洋的特殊环境，第3种驱动防滑控制方法更适合舰载机牵引车的驱动防滑控制。无论什么样的舰面条件(路面条件)，牵引车轮胎纵向力与轮胎滑转率的关系始终遵循先增后减的规律，因此满足滑模极值搜索算法(Extremum seeking control with sliding mode)的要求，能够自适应极值的漂移特性，快速准确地搜索到系统的最优值，即最大可用的轮胎纵向力。因此在线寻找最优滑转率的方法，不需要事先确定舰面最优滑转率和附着系数的前提下，对舰载机牵引车进行驱动防滑控制。而且针对具体的舰船舰面附着系数单一和不同舰面附着系数不同的情况，具有很强的适应性。

2.1 滑模极值搜索算法

滑模极值搜索算法是不考虑路面状况，根据轮胎纵向力—滑移率曲线先增后减的变化趋势始终保持不变的特性，在不依赖参考滑移率和最优附着系数的前提下，自适应甲板条件，通过不断搜寻曲线的极值点即最大可用的轮胎纵向力，快速搜索到曲线的最优值附近，从而实现提高牵引车驱动力的目的。控制程序如框图2所示：虚线框图部分是滑模极值搜索控制算法部分，驱动力矩Ttn是控制变量，牵引车驱动轮运动学模型根据式(6)创建，双线性模型根据实时滑转率的变化预估实时纵向附着系数，整车纵向运动学和动力学模型根据式(2)、式(3)以及文献(8)整合搭建。

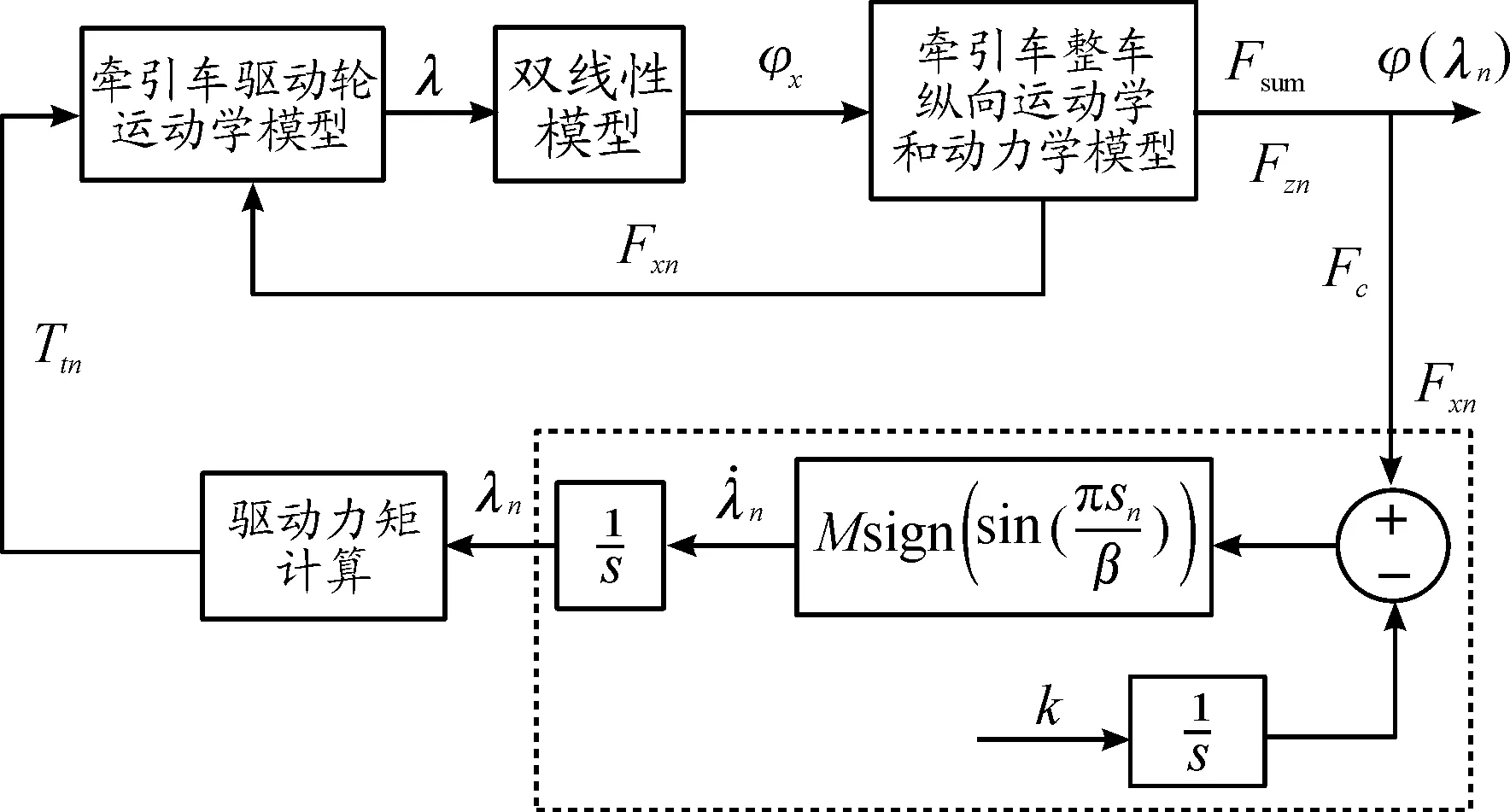
图2 滑模极值搜索算法控制程序框图

根据滑模极值搜索原理[19]，首先选择合适的滑模切换函数如下：

sn=Fxn(λn,αn)-kt

(8)

式中：Fxn是驱动轮轮胎的纵向力(n=1，2)；λn是驱动轮轮胎的滑转率；αn是驱动轮轮胎的侧偏角；k是一个常数值，决定了系统在滑模面上运动时的算法收敛速度。t代表时间参数。根据式(8)可知，通过滑模运动使得Fxn跟随线性递增时间函数kt的增长而增长，对sn求导可得：

(9)

(10)

M、β都是定值，且均大于零，sign(x)是符号函数。根据式(9)和式(10)可得：

(11)

与文献[20]证明类似，式(9)的滑模可到达条件为：

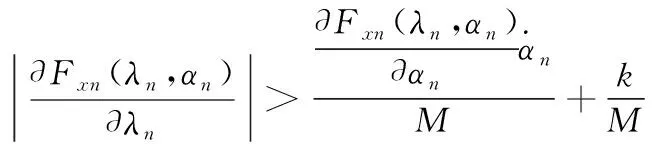
(12)

可以证明sn在任意初始值条件下，均收敛于滑模面θβ，其中θ是整数，θ=(0,±1,±2,…)，根据式(9)可得：

(13)

牵引车在甲板面上直线行驶时，根据式(13)可知，Fxn以斜率k的速率不断增大，在满足式(13)的前提下，不断搜寻驱动力的极值。牵引车行驶速度较低，假设忽略牵引车侧向运动，即αn=0，式(13)可以理解为：只要牵引力—滑移率的曲线斜率的值大于k/M，牵引力的值就会一直增加，直到接近极大值点，式(13)不再被满足，停止搜索。根据式(13)可知，系统存在多个滑模面，且滑模运动本身由于时间、空间滞后，系统惯性等诸多原因引起的抖振，使得滑模极值搜算法也具有稳态振荡这一难以避免的缺陷，算法产生稳态振荡的机理也较为复杂[19]。

2.2 驱动力矩计算

根据式(2)和式(6)可知:

(14)

(15)

将式(5)求导，并将式(14)和式(15)代入可得：

(16)

根据式(16)及式(10)可得控制后所需的稳定驱动力矩为：

Ttn=rd(Fxn+Fc/2)+

(17)

3 仿真实验

根据建立的理论模型，在Matlab/Simulink中建立轮毂电机驱动舰载机无杆式牵引车驱动防滑控制的仿真模型，对滑模极值搜索方法控制的驱动防滑效果进行了仿真验证。假设舰船在中等海况下[21]以10 m/s的速度匀速行驶，牵引车参数如表1所示。

表1 牵引车参数

为了能够与真实的舰面行驶条件更加接近，牵引车的峰值附着系数(φxp)和滑动附着系数(φxs)分别设置为0.75和0.95[22]，对目标牵引车驱动状态下的滑转率进行仿真。根据文献[8]分析可知，舰载机牵引车纵向行驶特性深受舰船运动规律的影响。为了更好地对比舰船运动对牵引车的影响，目标牵引车的未舰载情况通过将表示舰船运动的参数设置为0实现，即ls=[αsβsγs]=[0 0 0]。从而研究舰船运动对控制方法的有效性和牵引车滑转率的影响。图3所示是舰载未控制的牵引车的滑转率和滑模极值搜索算法控制的引车分别在舰载和未舰载情况下的滑转率。由于无杆式牵引车的等效质量包括一部分舰载机质量，因此数值较大，牵引车提供给舰载机的纵向牵引力也比较大[16]。基于以上原因的影响，舰载机牵引车的滑转率相对较小，这也在图3舰载未控制模型仿真中得到了验证。对比舰载和未舰载条件下的滑模极值搜索算法控制的牵引车滑转率，可以证明舰船运动对控制的时效性和稳定性都产生了明显的不利影响。

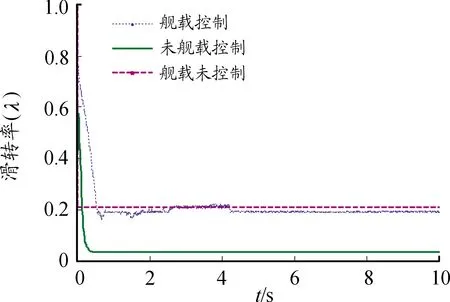
图3 高附着舰面驱动轮的滑转率曲线

考虑到低附着舰面能够更好地验证滑模极值搜索算法对牵引车驱动防滑控制的有效性，而且实际舰面也存在一定的磨损情况[22]，将峰值附着系数(φxp)和滑动附着系数(φxs)分别设置为0.55和0.75，使牵引车的滑转率达到一个较大的值。

图4是设置后的目标牵引车驱动轮滑转率曲线，在没有舰船运动的影响下，滑模极值搜索算法能够迅速达到最优滑转率附近。虽然受舰船运动的影响，控制算法的时效性受到一定的影响，但能够保证在5 s之内达到最优值附近，考虑到牵引车的行驶速度较慢，因此能够达到控制算法的时效性要求。

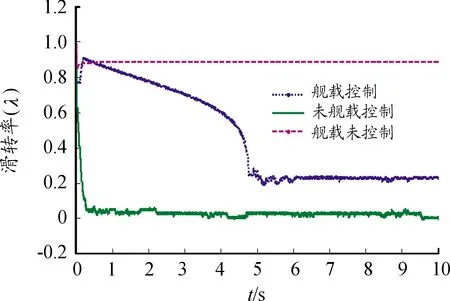
图4 低附着舰面牵引车滑转率曲线

图5反映了牵引车车身速度和驱动轮线速度，图6是舰船甲板面附着系数曲线。分析图5和图6可知：滑模极值搜索算法能够将车身速度控制在理想范围内，保证了滑转率在最优值附近，从而使得驱动轮能够获得较好的附着条件，达到最优的驱动力。滑模极值搜索算法控制下的牵引车在最优值附近存在稳态振荡问题，会导致轮毂电机电流变化频繁，影响电机的使用寿命。

图5 牵引车速度和驱动轮线速度曲线

图6 附着系数曲线

4 结论

由于舰船甲板面附着系数相对较大，舰载机牵引车行驶速度相对较慢，因此目标牵引车在完好的舰船甲板面上行驶时不会出现较大的滑转率。

舰船运动对牵引车纵向行驶的滑转率影响较大，使得驱动防滑控制的时效性以及鲁棒性变差。滑模极值搜索算法能够快速自动寻找到最优滑转率值的附近，不需要预先设置最优滑转率和识别舰面附着系数，能够保证舰载机无杆式牵引车的纵向行驶驱动力控制具有一定的鲁棒性和时效性。减轻算法的稳态振荡是该种算法未来改进的方向。