善用重要不等式解决最值问题

陈后万

(浙江省温州市洞头区第一中学 325700)

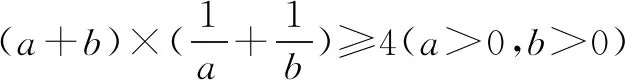
一 、条件易判断型

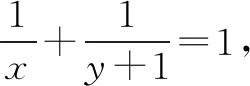
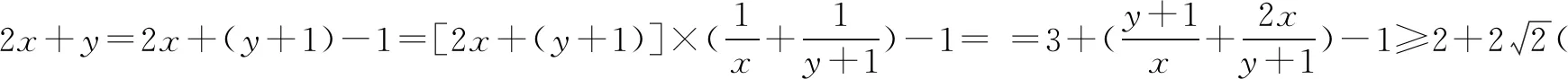
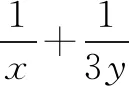
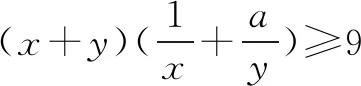
A.2 B.4 C.6 D.8

二、结构复杂化型

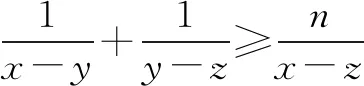
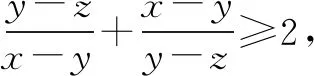
A.1 B.2 C.3 D.4

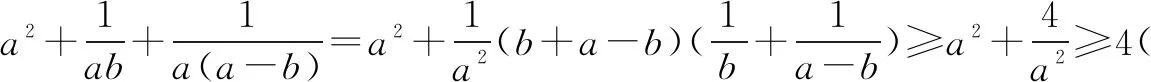
三、灵活巧变化型

例4(2012浙江卷)若正数x，y满足x+3y=5xy，则3x+4y的最小值是( ).

A. 245 B. 285 C. 5 D. 6

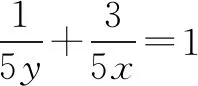
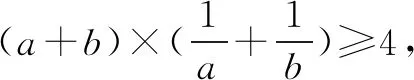
例5若正数x,y满足2xy+x-y-1=0，则2x+y的最小值为____.

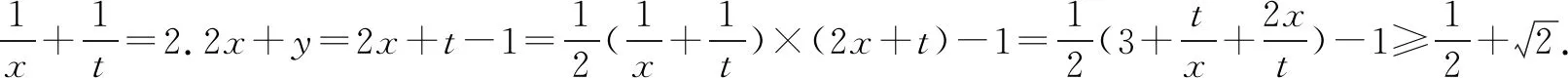
点评例5解法技巧性比较强，目的是为了消去常数，这样问题显然可以化归到例4类型问题处理.一般情况下，消元法、待定系数法、代换法可以解决此类问题，具体应用还要看题目本身的系数特点.

重要不等式在求函数最值(或值域)和证明不等式方面有着很多应用，极具简洁快捷功能.然而在实际运用过程中，同学们往往缺乏对基本不等式结构及其变形、变式的深入剖析，加上相关题目经常创新，更让学生一筹莫展、无从下手.为此,求解重要不等式问题的主要策略是善于总结、乐于总结，充分运用化归思想，抓住它的使用原则不放，构建基本不等式条件，高屋建瓴地使用重要不等式.