解数学题也要与时俱进

甘志国

(北京市丰台二中 100071)

新中国的第三代领导人江泽民(1926-)同志曾明确提出：“过去有许多做法和经验已经不适用了，要根据新的实践要求，重新学习，不断创新，与时俱进.”为了帮助教育者理解“与时俱进”的涵义，下面先介绍教育狂人陈忠联(1958-)在《陈忠联英豪教育报告会——将成功传给下一代》中讲述的故事《猫抓老鼠》：

有一天，一只猫在追一只老鼠，老鼠跑得很快，跑回老鼠洞去了，没有被猫抓住.其他的老鼠就很羡慕它：“哎呀！你到底是经过锻炼了的，连猫都抓不住你.”结果这只老鼠很得意.这个时候，这只猫在外面气得“喵、喵”直叫，……叫了半个小时以后它不叫了.老鼠又等了一个小时，外面一点声音都没有了，其他的老鼠就跟这只老鼠说：“诶，现在这只猫可能已经走掉了，我们可以出去了.”这只老鼠说：“不能出去，现在猫的技能也提高了，不能上当，得等一等！”又等了一个小时，狗在外面叫了.呃，这个时候，这只老鼠就跟其他老鼠说：“我们现在可以出去了！”那为什么说狗叫了就可以出去了呢？因为狗跟猫是不在一起玩的，“狗抓耗子多管闲事”.这个时候，这只老鼠就带领其他老鼠出洞了.结果刚刚一出老鼠洞，这只老鼠就被那只猫抓住了.这只老鼠想：反正我是已经死定了，已经被你抓到了，可是我要问一问这只猫是用什么计谋抓到我的？你看这只猫对老鼠怎么说哇：都什么年代了！21世纪了，我不换两招我哪有饭吃呀？我多学了一门外语，刚才这个狗叫是我学的！你看看，猫为了求生存，它都要转观念学狗叫，我们人的教育不与时俱进能行吗？你还是用传统的理念教现在的孩子显然是不行的！

笔者对与时俱进的理解是，与时俱进不是赶时髦，要不断学习(特别是新知识)，对旧的东西(也包括大家都感到习以为常的固定思维)要进行不断完善，甚至是革新，已达到最完美的地步.

题1(笔者所在学校某学期期末考试试题)在(2x-3y)15的展开式中，系数的绝对值最大的项是第几项？

参考答案(2x-3y)15展开式的通项

所以，当r=1,2,…,9时，trtr+2.得

t1t11>…>t16,

即(2x-3y)15的展开式中系数的绝对值最大的项是第10项.

一位学生的解法(2x-3y)15展开式的通项

所以，当r=1,2,…,9时，trtr+2.得

t1t11>…>t16.

即(2x-3y)15的展开式中系数的绝对值最大的项是第10项.

评分情况因为是学年期末统考，同校各班之间、同校与兄弟学校之间要比较成绩，所以笔者所在学校的高一、高二年级交叉阅卷，而这位阅卷老师只给了这位学生很少的分数，理由是“答案正确，理由不充分”.

实际上，“参考答案”的解法常规、流行(参见核心期刊发表的文章；当然，笔者在文献[2]中也给出了该类问题的完整结果)，但常规、流行的东西不一定是最完美的，有时也需要革新、完善，即与时俱进.

并且“参考答案”的解法还容易出错，这里顺便指出普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社，2009年第3版) (下简称《选修2-3》)第58页探究与发现《服从二项分布的随机变量取何值时概率最大》中的错误：

如果某射手每次射击击中目标的概率为0.8，每次射击的结果相互独立，那么他在10次射击中，最有可能击中目标几次？

设他在10次射击中，击中的次数为X.由于射击中每次射击的结果是相互独立的，因此X～B(10,0.8).于是恰好k次击中目标的概率为

从而

①

于是，有

当k<8.8时，P(X=k-1)8.8时，P(X=k-1)>P(X=k) .

②

由以上分析可知，他在10次射击中，最有可能8次击中目标.

以上叙述欠严谨，有两处应作改动：

下面再用上面“一位学生的解法”解答四道题(这四道题均出自文献[1])：

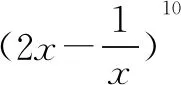
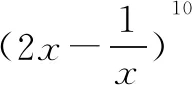
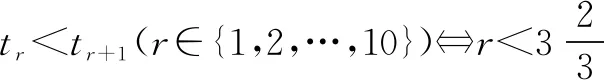
所以t1t5>…>t11.

tr

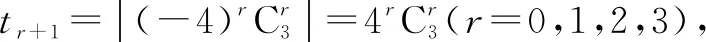
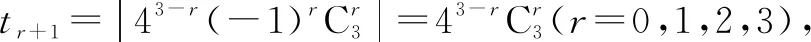
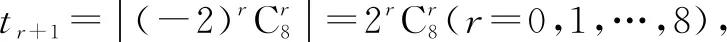
所以可得t1t8>t9.

下面再给出几个解数学题需要与时俱进的例子.

所以Sn=2n+1-3.

是不是这种类型的求和问题最后都可以统一成一个表达式，或者说这种问题毋须分类讨论！

证明以下证明也给出了此种题型毋须分类讨论的方法：

Sn=a1+a2+…+an=a1-f(1)+[f(1)+f(2)+…+f(n)]=a1-f(1)+Tn(n∈N*).

还可给出与定理1类似的结论：

题8已知数列{an}满足a1=1,an+1-an=n，求数列{an}的通项公式.

常规解法当n≥2时(因为下式中出现了an-1)，得

an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)

=1+[1+2+…+(n-1)]

巧妙解法约定a0=0，得

an=(a1-a0)+(a2-a1)+(a3-a2)+…+(an-an-1)

=1+[1+2+…+(n-1)]

常规解法当n≥2时(因为下式中出现了an-1，所以需要这样分类讨论)，得

再由a1=2，可得数列{an}的通项公式为an=2n.

数列{an}的通项公式为an=2n.

数列{an}的通项公式为an=n(n+1).

题11 求数列{(2n-1)·3n}的前n项和Sn.

解(错位相减法)

Sn=1·3+3·32+5·33+…+(2n-1)·3n,

③

3Sn=1·32+3·33+…+(2n-3)·3n+(2n-1)·3n+1.

④

③-④，得

-2Sn=3+2·32+2·33+…+2·3n-(2n-1)·3n+1,

⑤

-2Sn=3n+1-3-(2n-1)·3n+1-3,

Sn=(n-1)3n+1+3.

在该解答的④式中一定要列出(2n-3)·3n(否则③-④无法进行)，所以在④中n≥2；在⑤式中出现了2·32+2·33+…+2·3n，所以这里也需要n≥2的限制条件.也就是说，以上解答只适合n≥2的情形，即用错位相减法求数列前n项和时一般来说需要分类讨论.

本题若作如下改进，就不需要分类讨论了：

另解(错位相减法)Sn=1·3+3·32+5·33+…+(2n-1)·3n(n∈N*) ,

⑥

3Sn=1·32+3·33+…+(2n-3)·3n+(2n-1)·3n+1(n≥2,n∈N)

3Sn=-1·3+1·32+3·33+…+(2n-3)·3n+(2n-1)·3n+1+3(n∈N*) .

⑦

⑥-⑦，得-2Sn=2·3+2·32+2·33+…+2·3n-(2n-1)·3n+1-3,

-2Sn=3n+1-3-(2n-1)·3n+1-3,

Sn=(n-1)3n+1+3.

注普通高中课程标准实验教科书《数学5·必修·A版》(人民教育出版社，2007年第3版)第55页对等比数列(首项为a1公比为q)前n项和Sn公式的推导是正确的(无须分类讨论)：

Sn=a1+a1q+a1q2+…+a1qn-1,

⑧

qSn=a1q+a1q2+…+a1qn-1+a1qn⑨.

⑧-⑨，得(1-q)Sn=a1-a1qn.

在此推导的⑨式中，虽然出现了a1qn-1(n≥2)，但我们这样理解⑧-⑨就可以无须限定条件“n≥2”了：

(1-q)Sn=(a1+a1q+a1q2+…+a1qn-1)-(a1+a1q+a1q2+…+a1qn)+a1=a1-a1qn.