高观点下的高考函数试题探析

林松云

(福建省柘荣县第一中学 355300)

高等数学为背景的高考函数试题是高考中一道亮丽的风景线，内容、形式及解答上均有耳目一新的感觉.高等数学为背景的高考函数试题比传统题型有一些鲜明的特点：情景新颖、背景公平，设问方式灵活；能考查学生的创新能力和潜在的数学素质，体现“高考命题范围遵循教学大纲，又不拘泥于教学大纲”的改革精神.下面一起来欣赏高等数学为背景的高考函数试题.

一、以凸函数为背景

凸函数是高等数学非常重要的一类函数.自从导数引入高中数学教材后, 以凸函数为背景的考题备受命题者的青睐.

1.凸函数定义

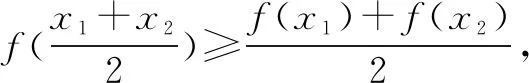
当定义中等号恒不成立时，我们称此函数在[a,b]上是严格上凸的(或严格下凸的).

2.凸函数的判断

(1)若在(a,b)内f″(x)<0，则f(x)在(a,b)为上凸；

(2)若在(a,b)内f″(x)>0，则f(x)在(a,b)为下凸.

3.高考试题分析

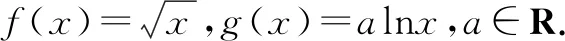
(1)若曲线f(x)与曲线g(x)相交，且在交点处有相同的切线，求a的值及该切线的方程；

(2)设函数h(x)=f(x)-g(x),当h(x)存在最小值时，求其最小值φ(a)的解析式；

(3)对(2)中的φ(a)和任意的a>0,b>0，证明：

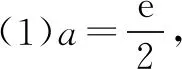
(2)φ(a)=2a(1-ln2a).

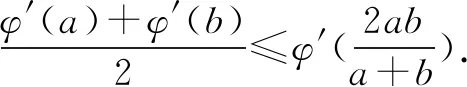
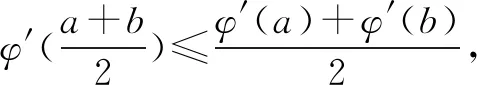
二、以极限为背景

极限是整个高等数学的基础，在高等数学中有很多重要的概念和方法都和极限有关系，并且在实际问题中极限也占有重要地位.因此对极限思想的考查也就成为重要内容之一.

1.函数在正无限处极限的定义

若对任意给定的ε>0，存在X>0，当x>X时总有|f(x)-A|<ε，就称常数A为f(x)在正无限远处的极限，或者称A是当x→+∞时f(x)的极限，记为：

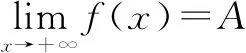
这时也称函数f(x)在正无限处极限存在.相仿地，可定义函数在负无限远处的极限.

2.高考试题分析

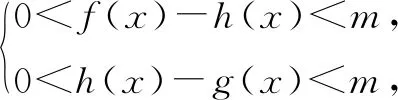
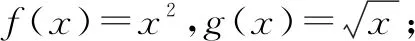
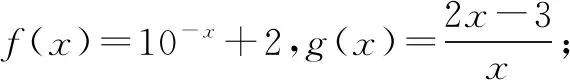
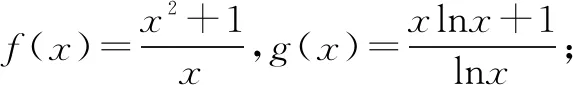
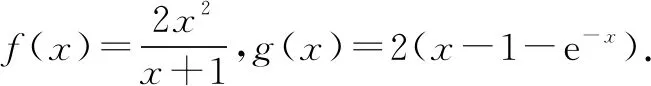
其中, 曲线y=f(x)和y=g(x)存在“分渐近线”的是( ).

A. ①④ B. ②③ C.②④ D.③④

答案：C.

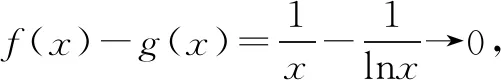
点评本题从大学函数在正无限处极限的定义出发，构造了分渐近线函数，目的是考查学生分析问题、解决问题的能力，考生需要抓住本质：若要存在分渐近线，则当x→∞时，有f(x)-g(x)→0且f(x)>h(x)>g(x).该题体现了极限思想，是高等数学中有限和无限思想的下放，是一道好题，思维灵活.

三、以微分学中的拉格朗日(中值)定理为背景

拉格朗日(中值)定理是几个微分中值定理中最重要的一个，是微分学应用的桥梁.在高等代数与数学分析中的一些理论推导中起着很重要的作用.

1.拉格朗日(中值)定理

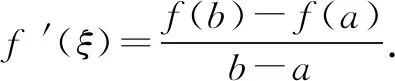
2.高考试题分析

例3(2017年高考全国卷2文科第21题)设函数f(x)=(1-x2)ex.

(1)讨论f(x)的单调性；

(2)当x≥0时，f(x)≤ax+1,求a的取值范围.

分析借助高数知识，能够巧妙地解决高考中难度较大的导数压轴题.

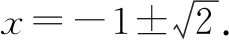
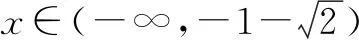
(2)首先，将x分成两类.

当x=0时，符合题意，所以a∈R；

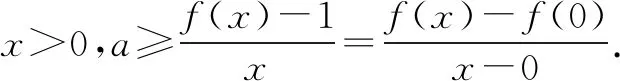
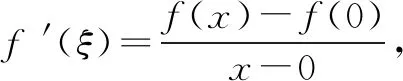
综上所述，a的取值范围为[1,+∞).

点评该题设计来源于微分学中的拉格朗日定理，用高等方法处理这题，还原了该题的命题思路，体现了初等数学与高等数学的“上联下靠”的关系，考查了中学数学的知识和方法，又考查了考生进入高等院校继续学习的潜能，是一道有特色鲜明的好题.

四、泰勒公式为背景的高考试题

1.泰勒公式

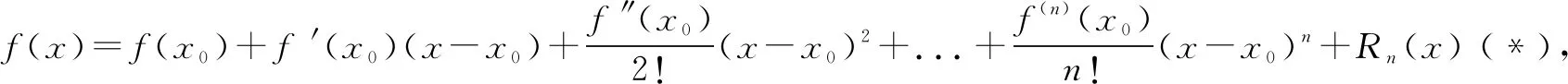
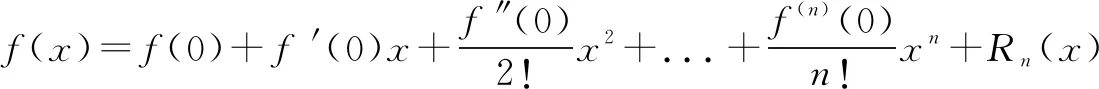
称此式为麦克劳林公式.

几个常见函数的泰勒展开式：

2.高考试题分析

例4(2017年高考全国卷Ⅲ理科第21题)已知函数f(x)=x-1-alnx.

(1)若f(x)≥0,求a的值；

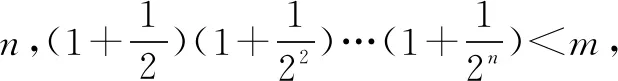
解析(1)略.

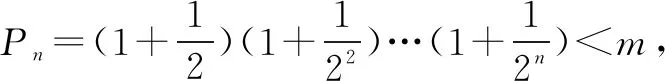
点评标准答案的解答是利用(1)的结论x-1-lnx≥0得出不等式ln(1+t)≤t，对Pn两边取对数，利用不等式ln(1+t)≤t得出m的最小值，转弯太多，考生不容易联想到，但直接用ex的泰勒展开式得出ex>1+x求解，简直就是秒杀.

例5(2014年全国新课标2理科第21题)设函数f(x)=ex-e-x-2x.

(1)讨论f(x)的单调性；

(2)设g(x)=f(2x)-4bf(x)，当x>0时，g(x)>0，求b的最大值；

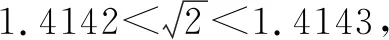
解析(1)(2)略.

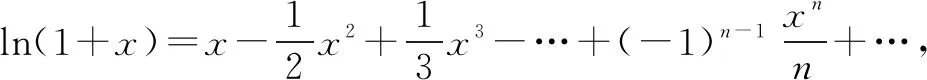
纵观近年的各地高考数学函数试题可知，以高等数学知识为背景的试题背景新，设问巧，既能考查中学数学的知识和数学思想方法，又能考查了考生进入高等院校继续学习的潜能，同时体现了高考的选拔功能，所以以高等数学知识为背景试题，成为每年高考题中的又一亮点、热点.教学中可适当让学生了解一些简单高等数学与初等数学结合的知识，既可以拓宽他们解题思路，提高分析问题，解决问题的能力，也可以为高等数学的学习打下良好的基础.