殊途同归求解一道2109年高考小题

杜海洋

(四川省成都经济技术开发区实验中学校 610100)

纵观近几年高考考查三角函数内容几乎都有一道涉及三角恒等变换的小题，一般属于容易或中档难度，这些小题往往题干简洁、精炼优美，内涵丰富，往往受到学生的喜爱而成为所谓的“网红”.三角变换是高中数学基本运算之一，但难点在于涉及公式多，角与角相互关系密切且错综复杂，解题时容易陷入方法无从选择的困境，有时思路不一样会导致解题长度不同，甚至进入泥潭不能自拔.下面笔者以一道高考试题为例，浅析三角变换常涉及到的处理策略，希望读者细细品味，在多种解法中，看看那些是由于公式选择不同造成的，那些是由切入点不同造成的，只有把这些问题弄清楚后才有助于我们去理解三角变换问题的解题精髓.

分析本题条件为正切形式，而结论是正弦形式，即已知角的函数名称与未知不同，则明显利用三角公式进行变换，消除两者的差异，那么思路方向不外乎常见的弦切互化.由于式子中存在两角的和与倍角关系，所以不难想到还要利用和角公式与倍角公式，这样就确定了解题的大方向.仔细推敲此题虽考查三角函数的求值，但渗透了逻辑推理和数学运算素养.采取转化法，涉及利用分类讨论和转化与化归思想解题.可见命题者对这道试题的独居用心.

【一招】弦化切

解法1由题意首先求得tanα的值，然后利用两角和差正余弦公式和二倍角公式将原问题转化为齐次式求值的问题，最后弦化切求得三角函数式的值即可.

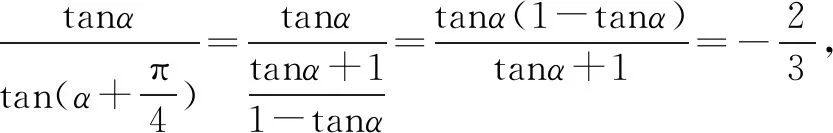
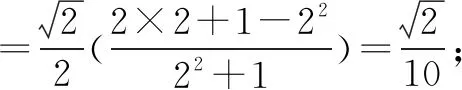
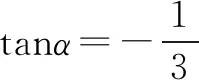
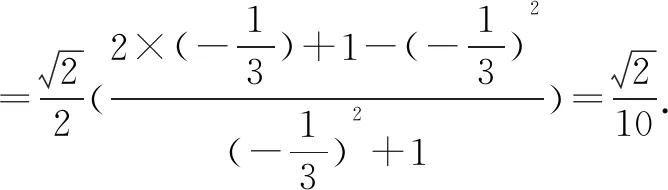
本解法充分利用了构成齐次式的思想，将2sinαcosα+cos2α-sin2α看成分母1=cos2α+sin2α是本法的关键之作，也是我们平时训练的常用的技巧之一.

解法2 万能公式1.

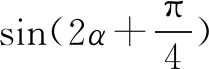
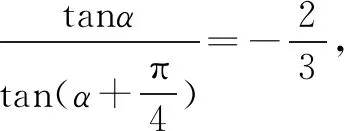
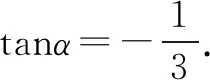
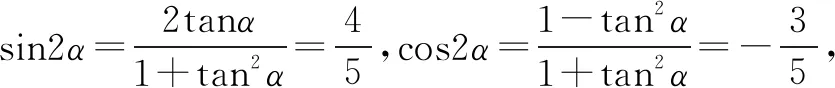
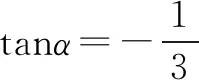
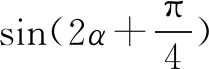
解法3 万能公式2.

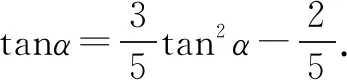
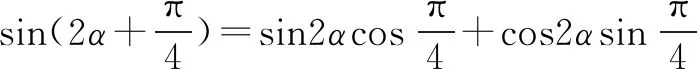
解法4 先将未知角向已知角进行变换，再进行“弦化切”.

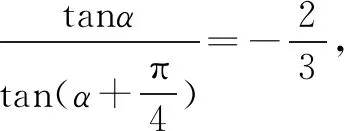
本法由题设和结论的角之间的关系，将未知角拆分向已知转化，这是角的变换最常见思路.

解法5 整体换元处理.

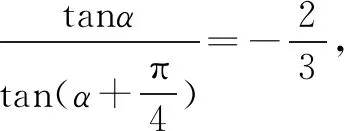
本法与法4一样，主要是在遇到式子结构复杂时，进行整体换元有助于简化运算，提高解题速度.

【二招】切化弦

解法6本法利用我们平时练的通性通法.出题者在设计上如用此法会产生分类讨论，可能在考场上因为简单的小题让考生久讨论产生心急的情绪，这也是命题者对考生全面考查的良苦之作.

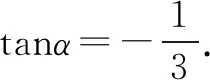
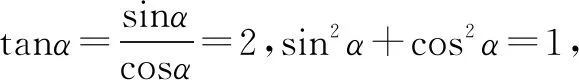
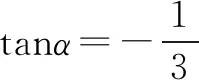
解法7 本法妙招在于直接通过切化弦，整理化简再合并得出结果，此法可称为妙

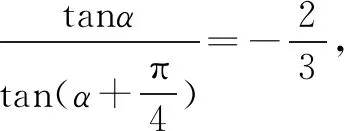
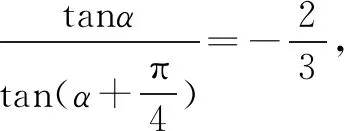
由(1)，(2)联立可得

此法妙招在于特殊角一般化，利用式子的结构特点，建立方程求解，思维难度较大.

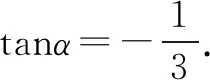
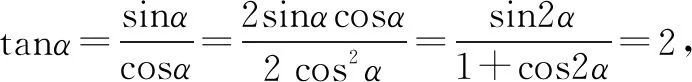
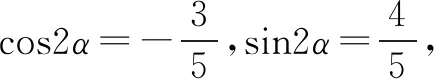
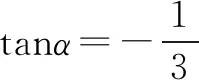
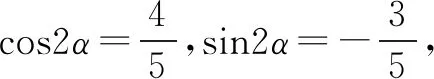
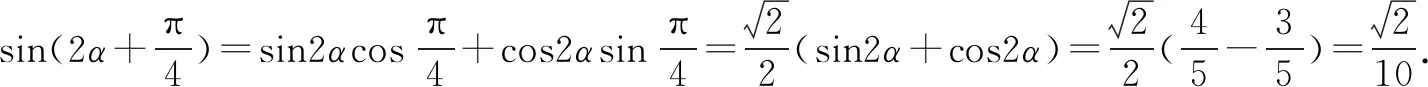
【三招】利用三角函数的定义

我们深知三角函数的定义是推导三角恒等变换的本源，所以从某种意义上讲，三角函数的定义功能更强大，也体现了数形结合的数学思想.

解法10 利用单位圆定义法.

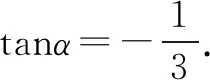
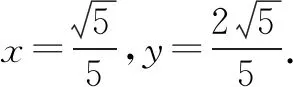
解法11 利用角的终边点定义法.

此法与角单位圆法类似.此处解法略，有兴趣的同学可做做.