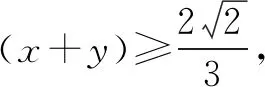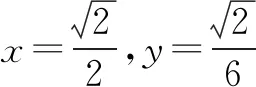差异分析巧妙转化——一道小题解题思路的探求

方仕友 王宝泉

(江苏省滨海中学 224500)

数学解题的过程可以看成是消除问题条件与解题目标之间的差异、消除所求解的问题与已知问题(已有知识)之间的差异的过程.为此，需要我们先找出差异，接下来，寻求二者之间的联系，在它们中间搭上一条解题的通道或者将所求解的问题转化为已知的问题从而解决它.这就需要我们针对具体的问题，不断地变换思维的视觉，纵横联系知识体系，全方位多角度地思考问题，以便“寻找差异、发现差异、消除差异”的解题方案快速形成.下面由一道小题来看数学解题思路探求中，如何应用“差异分析”，巧妙转化，形成解题的路径.

例若正数x,y满足x2+3xy=1，则x+y的最小值为____.

分析一注意到已知等式与要求最值的式中均含有两个变量x,y，与常见的一个变量的差异.可以考虑转化为一元最值问题.本题中的已知条件为关于x,y的等式，可以利用.于是有下面的解法一.

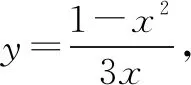
分析二等式x2+3xy=1为二次式，且为定值，欲求最值的x+y为一次式.与常有的“正数a,b满足ab=1，求a+b的最小值”类似.通过因式分解，尝试转化为基本不等式的应用问题.如下的解法二.

解法二因为x,y为正数，所以x+3y>0.

分析三注意到等式x2+3xy=1为二次式，且为定值，欲求最值的x+y为一次式.通过平方，消除两者间的差异，得到两个二次式.利用齐次式的关系及换元将问题转化为一元最值问题.利用导数求最值.

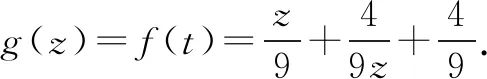
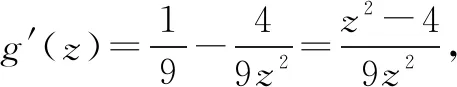
当1

当z>2时，g′(z)>0，g(z)单调递增.

分析五注意到已知等式与要求最值的式中均含有两个变量x,y，与解析几何中的直线与圆等二次曲线的位置关系问题的特点，以及方程组有解的要求，可以将其转化为方程组有解的问题.如下面的解法五.

消去y得，2x2-3tx+1=0有正数解.

由上面的分析与解法来看，数学解题分析的关键在于寻找差异、发现差异、合乎情理地分析差异、消除差异.