瓶中灌水时奇特发声的系列研究

李佳音 王 巍 钟 鸣 陆建隆

(1. 南京师范大学教师教育学院，江苏 南京 210000； 2. 南京师范大学物理科学与技术学院，江苏 南京 210000)

1 引言

在日常生活中，我们都会注意到这样一个现象——向热水瓶里灌水时，水流进入瓶中会发出声音，且这个声音是随着瓶中水量有规律地变化的.有经验的人甚至可以通过听声音判断出水瓶何时被灌满.还有一种现象，在很多公共场所的热水间里，水龙头出水口都会被裹上一段纱布，灌水时水流沿着纱布流入水杯，再沿杯壁流下，以防止热水喷溅导致烫伤.这种情况下就几乎听不到声音了.

针对这些现象，笔者进行了大量实验，并根据实际装置建立振动模型，将实验结果与理论计算结合，尝试回答以下4个问题： 瓶中灌水时，声音是如何产生的？是否有条件限制？在此过程中声音是否会发生变化？其变化规律是什么？

2 探究发声原理

2.1 实验设计

为方便模型的建立和单一变量的控制，笔者采用不同型号、形状规则的圆柱形量筒和一个可更换喷头的恒压水泵进行灌水实验，如图1，所用量筒筒壁上的刻度及其材料的透明度，都更有利于实验过程中的观察和即时数据的读取.实验过程中，将采音麦克风置于量筒口一侧，采集声音后将录音导入Adobe Audition进行音频分析.

图1 注水方式

当敲击一个灌有水的瓶子时，由于瓶身和瓶中水的振动，产生的声音频率与瓶中水量有关.那么灌水过程中的声音是由哪部分振动产生的呢？为此我们设计了一组预实验，将实验中所涉及的各个部分分开研究.通过向水位与筒口齐平的量筒继续灌水，就可以排除筒内空腔共振的干扰，改变量筒高度相当于改变了积水深度；通过向底部塞有吸水海绵的量筒内注水，可以排除下落水流进入积水层时产生声音的干扰，用线缠住海绵向上缓慢拉动，就可以连续改变量筒内空气柱的长度.此外，由于实验时量筒置于地面，考虑到地面振动的影响，可以在量筒底部垫上不同的材料，探究地面振动对本实验的干扰程度.

2.2 实验现象

在多次重复的灌水尝试之后，笔者发现声音的产生是需要一定条件的.若下落的水流较缓且呈稳定规则的柱状(可视作稳定层流)进入液面，如图2(a)，或者水流沿着瓶壁流下，则几乎没有声音，此时液面平静，水位均匀上升.只有当水流不稳定或间断性下落(可视作紊流)时，才会在水面上产生大量泡沫或单个大气泡，如图2(b)，并伴随有明显变化的声音.

图2 不同的水流形式

一次完整的灌水过程中，采集到声音频率在约为100～2000 Hz的范围内变化并逐渐升高，声音强度随水位升高而降低.

再根据实验设计将量筒内的积水与空气柱分开，实验发现仅改变积水深度时，声音频率没有明显变化，只有声音强度发生变化；而改变空气柱长度时，声音频率会随空气柱的缩短而升高，且这种频率的变化在水位靠近量筒口时更加明显.另外，在使用不同材质的量筒和地面实验时，声音特性的变化趋势不变，由此可知声音频率的变化主要和空气柱相关，声强大小和产生气泡相关.

2.3 原理分析

水在流动时几乎不产生声音，只有当水中有气泡产生、振动或破裂时，才会有声音产生.因此，瓶中灌水发声的必要条件就是，水流进入积水层时有气泡产生并振动.在研究这种气泡的水下振动时，我们根据Minneart理论建立了“单气泡振动模型”，把下落的水流视作大量连续的小水滴，单个水滴进入液面后夹带一部分空气，如图3.这个过程类似于向水中掷石子，关键在于让空气进入水中形成气泡.图4依次是实拍单个水滴滴入平静液面时水面凹陷、收缩、产生气泡、气泡破裂的过程.

图3 水下气泡产生示意图

图4 实拍水下气泡产生的过程

对单个水下气泡进行分析，可以通过弹簧球系统类推，其恢复力由气压与表面张力组成，惯性力由周围液体的有效质量引起.考虑半径不可忽略的球形振动气泡，其半径随时间的变化可设为

r(t)=r0+q(t)，

(1)

其中q(t)为半径随时间的扰动量，即弹簧球的振动量，可建立谐波振动线性模型方程

(2)

其中Fb为由液体压强而产生的外部压力，β为阻尼率，ω0为气泡谐振频率，mbrad=4πr03ρ为气泡有效振动质量.[1]

可见气泡振动频率与有效振动质量、液体阻尼、外部压力有关，分别对应气泡半径、液体种类、气泡位置.由于水流连续下落会在液面下产生大量半径不同、位置深浅不同的气泡.这些气泡振动、破裂所发出的声音频率混杂，没有明显的变化规律，所以气泡的振动幅度、密集程度直接决定了注水时声音的强度，对频率变化影响不显著.通过以上的实验和理论分析，笔者发现声音频率随水位上升而升高，是由于不同长度空气柱振动的固有频率不同，故水中气泡发生共振时，产生的声音与空气柱长度相关.

2.4 构建空气柱振动模型

若将实验所用玻璃量筒视为刚性容器，则空气柱仅发生纵向振动，且满足一般振动方程

ξ(t,x)=(Acoskx+Bsinkx)cos(ωt-φ)，

(3)

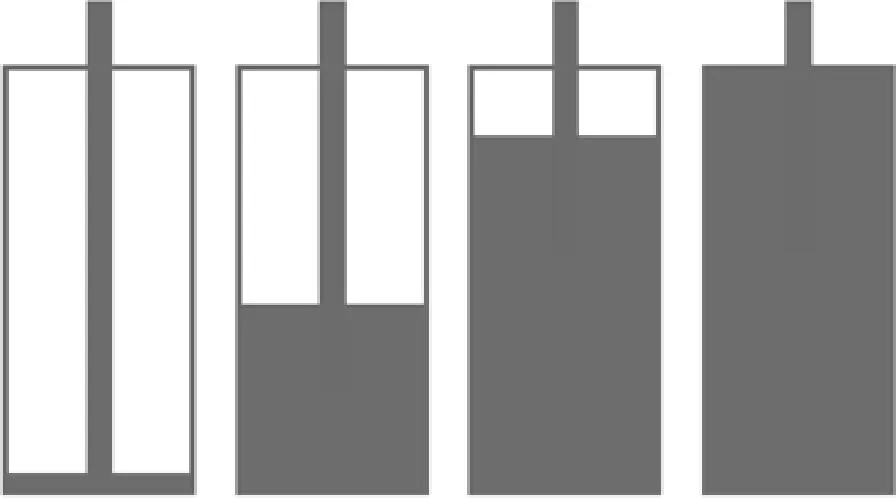
图5 空气腔共振示意图

(4)

解得空气柱振动的简正频率为

(5)

其中n=1,2,3,…且n=1时λ为基频波长.

考虑到空气柱振动同时还会向空间辐射声波，相当于在量筒内的空气柱上附加振动质量，故需将管长修正为l=l0+l=l0+1.7r.[3]

代入简正频率公式，取n=1时，可得空气柱振动基频为

(6)

因此当水位上升，即空气柱缩短时，声音频率会随时间升高，若n取不同的正整数，还会出现相似变化趋势的谐频，如图6，(a)亮条纹为实际测得数据曲线，(b)为根据计算结果绘出的曲线，其中曲线由下向上分别表示n=1，2，3，4 时，频率f随时间t的变化规律.另外，通过改变水流速度(流量Q)和瓶身尺寸(高度h和半径r)，也可以改变声音的频率.

图6 简正频率随时间的变化

3 控制变量实验

根据上述分析结论，笔者设计了一系列控制变量实验，分别改变水流流速(调节恒压阀挡位即可)、出水口尺寸(更换不同口径的出水口)、瓶身容量(采用不同型号的量筒)和瓶身形状(使用不同形状的等高玻璃瓶)，探究产生声音的声强和频率随时间的变化规律.

3.1 声音频率与水流速度的关系

注水过程中产生声音的频率随时间(水位升高)逐渐升高，且测得的声音频率会略高于理论值.这一现象在水位靠近量筒口时愈发明显，如图7，频率平缓升高时实验数据与计算值符合度高，而频率快速升高阶段实验采得的频率(散点)皆高于理论曲线.

图7 频率随时间变化曲线(声音特性与水流速度的关系)

由图可见，实验与理论存在误差，这部分误差的存在主要是两部分造成，一是水流流速较大，下落时会在液面产生大量气泡和泡沫，使得实际液面高度高于根据流量计算得到的液面高度，故实际空气柱长度偏小；二是当液面与量筒口十分接近时，计算空气柱长度的修正项(附加质量)误差渐大，同样使得实际振动的空气柱长度比代入计算时的长度短.

3.2 声强与水流速度的关系

注水过程中，同一时刻的水流流速越大，不仅频率越高，而且声强越大，如图8.

图8 声音特性与水流速度的关系

对完整过程进行快速傅立叶分析后，图像中声强尖峰出现在0～500 Hz之间，对应了频率随时间变化曲线中平缓升高部分的频率范围，这是声音在这一频率范围长时间累积出现的结果.

3.3 声音特性与出水口孔径关系

随着出水口孔径的增大水流截面半径，也增大水流下落后与液面的接触面积增大，同时在流速不变的前提下，流量增大，所以单位时间内产生的气泡数增多，声强增大，但声音频率不变，如图9.

图9 声音特性与水流半径的关系

3.4 声音特性与量筒尺寸关系

根据理论计算结果，增大量筒截面半径或量筒高度后，声音频率的变化趋势是相同的，所以实验中直接使用不同规格的玻璃量筒进行实验，即同时改变了半径和高度两个变量.

对完整注水过程作快速傅立叶分析，发现随着量筒容量变大，声音频率降低，声强增大，如图10.

图10 声音特性与瓶身尺寸的关系

3.5 声音特性与瓶身形状关系

在改变瓶身形状(控制玻璃瓶高度相等)时，时域图(频率随时间的变化曲线，颜色明暗表示声强大小，亮度越高声强越大)形状发生明显变化，基本频率变化规律不变，而谐频的变化趋势与瓶身形状有关，如图11.

我们认为这是由于不同形状的玻璃瓶使得共振腔的边界条件发生了改变，简正频率中的谐频随之改变(系数不再是2n-1)，但对基频变化规律没有影响.

探究结论：在一次完整的灌水过程中，随着水位的升高，空气柱缩短，声强随时间降低，频率随时间升高.声强与流速和出水口孔径正相关(流量和水流半径越大，产生的气泡越密集，振动幅度越大)；声音频率与瓶身尺寸(高度、半径)负相关.

图11 声音特性与瓶身形状的关系

4 总结与反思

通过实验和理论计算，我们得出填充瓶子时所发出的声音由气泡振动和空气柱振动两部分产生，水中有气泡产生是产生声音的必要条件.同时产生气泡的大小和密集程度决定了声强大小，而频率变化则主要是由空气柱共振体现.

本文的分析皆是建立在规则圆柱形刚性容器的基础上，而对于生活中常用的细颈瓶状容器或其他不规则容器，其发声基本原理相同，但计算频率时需要根据实际形状和尺寸设置边界条件.

另外，考虑到实际灌水时，由于下落水流的存在，空气柱不是严格的完整棒状.为此笔者补充了一组对照实验，在量筒中分别竖直插入1～5根细塑料圆棍，在此基础上进行灌水，声音频率不会出现明显变化.所以为简化模型，灌水时将量筒内的空气柱简化为棒振动是较为合理的.