物理化学课程教学中如何设置情境问题

林洁丽，李杰森，刘弋潞

（佛山科学技术学院，环境与化学工程学院，广东 佛山 528000）

《物理化学》课程属于高校理工科的基础课范畴，介于专业基础课和专业课程之间，其教学需要注重基本知识和基本能力的培养，为后继课程的教学打下坚实的理论基础。物理化学是四大化学的灵魂［1］。我们课题组对该课程提出了以学生为本的教学模式［2］和熏陶式主动型教学模式［3］，能够较大程度提高课堂学习和教学效率。物理化学关注物理量与化学反应规律的关系，通过对系统物理性质的研究探索化学变化的规律，所以在学习时特别要注意掌握公式的物理意义和使用条件，但该课程不仅跨学科多、理论性强、公式多且内容枯燥复杂，导致公式的物理意义和使用条件非常容易被学生混淆，因此我们以相变过程为例介绍如何掌握热力学公式的适用条件，使学生更好理解可逆过程的特点［4］。在加强教学实践学时的高校改革进程中［3］，物理化学因学时受限、教学进度变快，易造成学生听懂不会做的局面，在解题过程常遇到思维受阻的现象［5］。最近我们提出新的教学理念［6］，以热力学定律公式的应用为例介绍了创造情境、提出问题、等待顿悟的三步曲的教学改革，教学效果是令人满意的，不仅提高学习积极性和解题觉悟能力，而且激发培养了学生的创造性思维能力。本文结合这些教学理念以化学平衡为例介绍如何有效地设置情境问题，使学生更好地掌握相关知识。

1 设置问题遵守的原则

物理化学是一门两多 （概念多和公式多）和三强 （理论性强、系统性强和逻辑性强）的学科，其中公式的应用条件既严格又比较抽象，是使学生普遍感到困难较大的一门课程。加之在向应用型大学转型过程中，课程体系又压缩了其理论教学比重。例如我校化工类人才培养计划中物理化学的教学只有64学时。有限的教学学时与广泛的教学内容形成矛盾。教学内容包括化学热力学、多组分系统、化学平衡、相平衡、电化学、化学动力学、界面化学和胶体化学等。所以教学过程注重 “三基”教学（包括基础知识、基本理论、基本技能，化学平衡章节只有6学时，其 “三基”如表1所示），重点把 “三基”内容讲清楚，适当介绍原理公式在相关专业的应用，弱化公式、定理和理论推导证明的教学。即便如此，我们也是断不能采纳填鸭式教学，而是采取创造情境、提出问题、等待顿悟的三步曲的教学思路。这其中，问题的提出是最关键的，不仅要贴合情境还要吸引学生完成对知识的顿悟，而且还不能因复杂而占用过多时间。具体要求是：学生先遇到问题，再通过课堂听课或者自学来直接感知基础知识和基本理论，然后通过解决设置的问题和完成习题作业来体验基本技能，实现顿悟，最后达到既能清晰阐明知识结构又能梳理知识结构的目标。在他们学习过程我们需要不断给予提示情境内容，安排好学习解决问题的进度，举例说明相关的因素。

表1 化学平衡章节的 “三基”要求

2 设置情境问题的分类

物理化学是从研究化学现象和物理现象之间的相互联系入手再探索化学变化中具有普遍性的基本规律，目的是运用物理学的理论和方法对化学现象做出理论和定量的探讨。所以学习中设置的情境问题根据来源可以分为生活中案例、实验课程中问题、教材习题和例题。例如，在介绍多组分系统的化学势概念前可以设置 “在北方，冬天为什么在路上撒盐”的生活问题，该问题也是多组分系统依数性的应用；学习界面化学章节时，设置 “农民为什么要锄地”这样一个典型的生活案例，引出表面张力的应用。根据情境内容和学习目标，问题可以分为：引出概念问题、应用条件问题、综合应用问题。如在相平衡章节介绍重要概念焓和相变焓前可以让先学生解答 “某温度的水和冰混合后的温度”［6］的问题。

3 设置情境问题的举例

3.1 引出概念问题

化学平衡是用反应吉布斯函数值是否为零判断，平衡移动是借助反应的等温方程式以及平衡常数的计算来判断反应吉布斯函数的变化。化学热力学章节介绍了吉布斯函数概念，本章重要概念是摩尔反应吉布斯函数和标准平衡常数。教学思路包括情境、问题、顿悟，问题抛出前需提供一定的情境，即判据：对化学反应系统（其中B表示物质成分，νB表示化学计量系数），属于多组分系统，各物质的化学势μB满足 （1）时，系统处在平衡状态。

我们设置的问题是：我们为什么能够吃饱饭？这也属于典型的生活案例问题。

我们的食物基本从农作物而来，农作物需要肥料。氨可以制成氮肥，也可以作成化工原料，这问题转变为回答：氨能否由氮气和氢气合成？

由附录九得到常温标准态下各物质N2()g、H2()g、NH3（g）的摩尔生成吉布斯函数值分别是0、0、-16.45kJ·mol-1，所以：

这样就不但回答了问题 （因为有合成氨的反应），而且引出了标准摩尔反应吉布斯函数的概念。第二个概念是标准平衡常数。我们该设置什么问题呢？反应 （2）能发生，但是反应程度如何呢？用什么物理量衡量？

3.2 标准平衡常数的应用条件问题

已知反应ZnS(s)+H2(g) ＝Zn( s)+H2S(g)在1000K下的标准摩尔反应吉布斯函数［7］

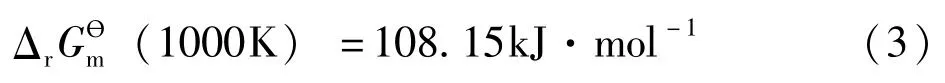
则当压力为常压p0的H2()g通过加热为1000K的ZnS()s时，H2S()g的分压为多少？

根据提供的情境内容可以得出该反应不能向右进行，不会生成H2S()g。如果H2S()g气压为0，则根据体系的标准平衡常数Kө表达式：

Kө应该等于0，这显然不合理。因此我们要回归到标准平衡常数Kө的定义式：

更科学的做法是把式 （3）代进式 （5）得到Kө＝2.242×10-6。假设平衡时H2S()g气压为pH2S，则H2()g气压为pH2＝ （p0-pH2S），再代进式 （4-2）得到：

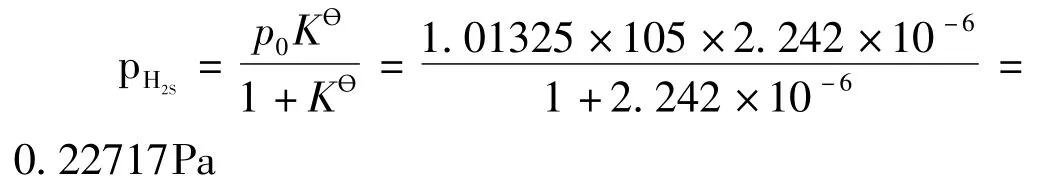
这样就说明了标准平衡常数的定义式 （5）和常用计算式 （4-1）的区别，并且总结：标准平衡常数是特征常数，与反应本性、温度相关，而与浓度、压力无关；可以延伸到这样的常识 “根据标准平衡常数的大小可以判断反应进行的完全程度”：

当Kө≥107时，反应完全进行；当Kө≤10-7时，反应几乎不可能发生；当10-7≤Kө≤10-7时，可以通过改变条件来促进反应进行。对于3.1节内容的式 （2）合成氨反应的标准平衡常数为6.636，属于第三种情形，需要改变条件促进氨的合成，常见的就是高温高压和添加催化剂，章节后面内容介绍升温可以提高标准平衡常数。

3.3 综合应用问题

化学平衡的主线是等温方程式的应用，延伸到真实气体的反应平衡移动问题和不同温度下的平衡移动问题。

3.3.1 延伸到真实气体的反应问题

关于真实气体的反应，我们设置教材的习题为问题。在某温度和某压力下反应达到平衡：

若压力提高两倍，则该反应会向哪边移动？

显然是考查压力对反应体系的影响。根据化学反应的等温方程式：

计算升压后ΔrGm的变化，若变为小于零，则反应向右移动；反之向左移动。对该问题，我们提供的情境内容除 （4-1）、（4-2）、（5）、（6）外还有用摩尔分数yB表示的经验平衡常数Ky：

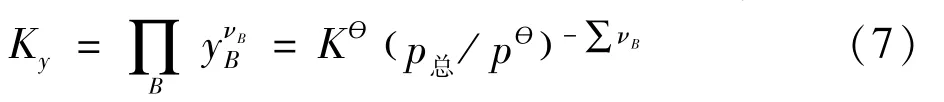
根据情境内容，因温度不变，说明标准平衡常数Kө也不变，同时不难发现由于该反应的∑ νB=0，因此压力发生变化时，不变的Kө使得Ky也不变，意味着系统的气体的组成不变，所以平衡不发生移动。

但是如果反应气体是真实气体，那么式 （7）还成立吗？成立，但不能直接用它判断真实气体的平衡移动，因为真实气体的标准平衡常数Kө＇表达式为：

与式 （4-1）比较，引入逸度因子φB后，真实气体和理想气体的标准平衡常数的关系为：

式 （9）的Kө也是理想气体的标准平衡常数，表达式中的物质压力对应平衡状态的值，温度不变时，真实气体的Kө＇不变，因此当气压增大时，若Kφ＞1时，要求变小，即向反应物方向移动；若Kφ=1时，不变，即平衡不移动；若Kφ＜1时，要求变大，即向生成物方向移动。或者把 （9）代进 （7）得到：

由式 （10），温度不变，总压力变化下，当Kφ＞1时，Ky变小，即向反应物方向移动；若Kφ=1时，Ky不变，即平衡不移动；若Kφ＜1时，Ky变大，即向生成物方向移动。结论与上面分析一致。

3.3.2 温度对标准平衡常数的影响问题

不同温度下的反应平衡问题，我们选择教材［7］的例题为设置的问题，即：

石灰石烧成生石灰的反应为：

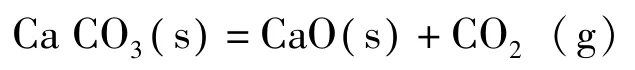
常温T1常压p1下，计算该反应的摩尔反应吉布斯函数：＝130.40kJ·mol-1＞0，该条件下是不能发生反应的。需要加热提高温度，使得该温度下产生的CO2（g）的压力达到环境压力，这时石灰石快速分解。求该分解的温度。

设置该问题前的情境内容除了式 （4-1）、（5）、（6）外，还有范特霍夫方程：

由题意可求常温下的Kө，假设分解反应的热容变化为零，则可把标准摩尔反应焓=178.32kJ·mol-1视为常数，对式 （11）进行定积分求解可以得到分解温度T2与两个不同温度下的标准平衡常数的关系式：

T2＝1110K（837℃）

解答后，引导学生对本章相关知识内容发生顿悟，归纳以下结论：温度对标准平衡常数有显著的影响，不仅能改变反应的平衡转化率，还能改变反应的方向。

4 结论

针对物理化学的课程特点和应用性专业学时数相对较少的现实情况，在教学中充分利用问题的预设思路，引导学生学会整合教材知识点并灵活运用它们来解决化学问题。以化学平衡为例，通过生活案例、习题、例题，以引出概念为目的，以灵活应用基本知识点为目标，让学生掌握 “三基”内容，顿悟解决化学平衡的物理化学基本知识点，提高解决实际问题的能力。