直流配电网线路故障测距新方法研究

谢紫汉

（国网湖南省电力公司郴州供电分公司，湖南 郴州 423000）

0 引 言

直流配电网是由直流母线直接给直流负荷进行供电，不需要通过逆变器进行转换供电，由于直流负荷线损率小、可靠性高、不需要变频控制器进行控制、可以与分布式电源进行兼容，可满足当前配电网络快速发展的需求。因此，近年来直流电网快速发展，广泛应用在电力系统中。直流配电网线路发生故障时，需要快速检测与恢复故障位置机械能，以免线路故障范围进一步扩大，造成严重的电力安全事故。因此，准确测量直流配电网线路故障的距离，对加快恢复直流配电网正常运行具有重要意义。目前，国外的直流线路故障测距方法大部分适合高压长距离的直流输电系统，不适合线路距离比较短的直流配电网系统，无法准确测量直流配电网故障的距离。行波测距法利用故障线路上波阻抗不连续节点的反射特点进行测量，由于故障暂态信号在网络经过多次发射，无法准确识别故障行波，需要多次进行采样，增加了测量成本[1]。因此，需要研究新型直流配电网线路故障测距方法，提高线路故障距离测量的准确性和及时性。

1 直流配电网线路故障测距常见方法

1.1 行波测距法

行波测距法是根据行波理论进行测距的方法，在故障发生线路初始端注入脉冲信号，根据脉冲信号在检测装置到故障点的往返时间测定距离。如果线路出现故障，故障点受到附近电源的影响，故障线路出现接近光速传播的电压和电流行波，根据初始点到达检测母线的时间和故障点的反射波确定到达检测母线的时间差、单端行波故障距离确定故障距离。线路故障行波测距的原理是利用最具鲁棒性的单端阻抗确定故障发生区段，再利用小波变换的电流行波法计算故障距离。鲁棒性指在有扰动和没有建立系统动力学的条件下，电力系统保持稳定性的能力。鲁棒性阻抗测距方法可以确定故障发生的范围，其计算误差不会超过线路总长度的10%，加之行波测距的精确定位，其误差范围不会超过1 km。

1.2 两端测距法

两端测距法是同时利用线路两端的电气量实现的故障测距法。由于这种算法是利用两端电流电压推算到故障点电压相等的条件获得故障位置信息，因此从原理上不存在过渡电阻和对侧系统阻抗影响的问题。在两端测距法中，因为必须借助通信技术获取对侧的数据信息，所以就产生了两端数据的同步问题。为解决两端数据同步问题，在测量过程中需要投入时钟同步设备，并设置专用的信息通道，确保测量两端的数据信息同步，在一定程度上增加了测距成本[2]。

1.3 人工神经网络测距法

人工神经网络测距方法是利用人工神经网络对线路故障点距离进行测量。人工神经网络模仿人脑神经元，构建一种简单的神经网络模型，按照不同的连接方式构建不同的网络，通过网络的变换和动力学行为获得并行分布式的信息处理能力。根据网络连接的神经元特点、网络连接的拓扑结构、学习类型可以构建不同的模型。人工神经网络本质上是一种运算模型，由大量节点（神经元）构成，网络中的每一个节点代表了一种特定输出函数，并按照一定的学习算法调整网络的权值矩阵。配电线路故障测距是单端故障电气量与故障点之间的对应关系，将人工神经网络运用在配电线路故障检测过程中，可以利用人工神经网络的非线性映射能，实现配电网线路故障测距功能。但是，人工神经网络测距方法需要利用大量已知的数据对神经网络进行训练，测距误差受样品大小的影响。此外，人工神经网络的模型与实际线路故障的数据有一定的误差，其误差可能影响最终测距误差[3]。

2 直流配电网线路故障测距新方法

通过分析发现，上述3种常见的直线配电网线路故障测距方法存在测量成本高、测距误差比较大的问题，因此需要研究一种新的直流配电网线路故障测距方法。本文提出一种离线注入测距法，这种测量方法是利用离线外接设备，也就是测距模块为直流配电网线路故障测距提供信号，如果直流配电网出现短路故障，断路器立即断开，故障区域内将测距模块的电容和电感与线路电阻等效为RLC串联电路。根据RLC串联电路零输入响应的特点，在电容电流峰值时，电流感应的瞬时电压为0的特性，列出t时间内的守恒方程，得出直流配电网线路故障距离和过度电阻。直流线路故障测距模块由电源电压、电容C、可调节电感L以及开关S1、S2等构成。为了得到比较精准的数据信息，测距模块可以重复测量电容电压和电流值，取多次测量的平均值[4]。

2.1 离散化处理

由于直流配电网线路的电容放电过程中电流曲线表现出非线性特征，直接将采样点带入计算公式中会产生一定的误差，因此需要对其离散化处理，对采用的数据进行调整，计算公式如下：

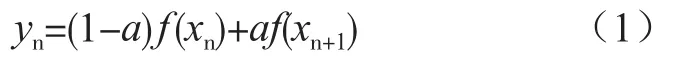
式（1）中，f(xn)表示第n次的采样结果，f(xn+1)表示第n+1次采样结果，yn表示调整后的第n次采样结果，a表示调整系数，取值范围为0＜a＜1。当0＜a＜0.5时，yn＜(xn+xn+1)/2；当a=0.5时，则yn=(xn+xn+1)/2；当0.5＜a＜1时，则yn＞(xn+xn+1)/2。因此，计算时可以调整系数，使yn=f[(xn+xn+1)/2]。

2.2 确定测距模块电感参数

本文采用RLC二阶电路零输入响应特点计算等效电阻，并通过能量守恒定律确定故障测距算法，所以测距模块的电容初始电压不会影响直流线路故障测距精度，电容值取值大的情况也不会影响测距结果。RLC电路等效电阻比较大时，二阶零输入相应的电流上升率比较快，测距模块电感则需要减少电容电流上升速度，降低系统采样频率。如果给定采样频率、电感参数设置不合理，则可能造成较大的误差，所以需要增加RLC网络等效电感量，降低采样频次。电感参数的确定步骤如下：首先给定任意一个电感值，计算出等效电阻值，根据等效电阻的数值和采样频率，确定下一个测量可采用的电感值；然后对测距电感数值进行调整，确保测距模块在采样频率比较低的情况下取得比较高的测距精度[5]。

2.3 线路故障测距流程

直流配电网线路的永久性故障可以分为正极短路故障、负极短路故障、双极短路故障3种。线路故障测距时，如果检测到直流配电网线路发生短路故障，则立即切断直流断路器，切断线路功率的传输。然后闭合断路器开关，测距模块的电压源向电容充电，充电结束后断开闭合开关，根据故障类别，确定闭合开关S1、S2的组合。如果是单级正极接地故障，则同时闭合开关S1到1端、S2到0端；如果是单级负极接地故障，则闭合开关S1到0端、S2到2端；如果是双极短路故障，则需要闭合开关S1到1端、S2到2端。最后采集电容放电过程中的最大值和电压值，根据RLC等效电阻，确调整测距模块的电感值。为了提高测距精度，需要多次测量线路故障的距离。

2.4 仿真验证

为了进一步验证离线注入测距方法的准确性和实用性，需要利用计算机仿真软件进行验证。在测距过程中，还要考虑线路分布电容、采样频率及接地短路故障对测量结果的影响。考虑直流配电线路分布电容对故障测距的影响，设置过渡电阻为100 Ω，故障线路全长为3 km，接地短路故障测距误差在分布电容范围在10～60 pF波动很校，分布电容对接地短路故障测距结果的影响几乎可以忽略不计；采样频率在10 kHz时，故障测量距离的误差比较大；采样频率超过20 kHz的时候，测量误差距离比较小，所以仿真试验采样频率设置为20～60 kHz，过渡电阻数值范围设置为0～120 Ω，在这个范围内的故障测量误差控制在0.7%以内，测量精度比较高。本文研究的新型直流线路故障测拒方法可以实现对故障点的精确定位，因此短路故障测距误差比较小，可以忽略不计。

仿真时，需在软件中构建双端直流配电网模型，将数据导入仿真软件进行验证，仿真参数如表1所示。

表1 仿真参数

2.5 对比验证

为了进一步验证离线注入测距法优劣，与行波测距法、两端测距法和人工网络测距法进行对比。行波测距法测量短距离配电网线路故障时，往往利用小波分析理论判断波头，再根据行波发送端在故障点之间往返一次的时间计算故障距离，但是其对采样频率要求比较高，仿真模型采用必须达到1 000 kHz，故障距离测量误差控制在2%以内；两端测距法对直流配电网进线路进行故障测距，采样频率设置为20 kHz，配电网线路故障测距误差控制在1%以内，适用于换流器的直流母线并联的大电容；人工神经网络测距方法需要采集大量的直流配电线路数据信息。同时，通过测距类型、采样频率和测距误差3个指标对比分析不同的测距方法，对比结果如表2所示。

表2 不同测距方法对比结果统计

通过表2可以看出，不考虑噪声、电磁感应等因素的影响，行波法和人工网络测距方法的误差在2%以内，但是采用的频率高于两端测距法和离心注入测距法。

3 结 论

离线注入测距法应用在直线配电网线故障测距过程中，测距模块简单，可以重复测量，测距可靠性和准确性比较高，采样频率低，成本比较低。与其他直流配电网故障测距方法相比，该方法采样频率要求比较低、测距精度高，在直线配电网线路故障测距中具有一定的应用价值。