肋环形加劲浅球壳缩尺模型的自振特性分析

高 展，贾冬云，刘健文，王 涛

(安徽工业大学建筑工程学院，安徽马鞍山243032)

冶金、石化等企业在生产运输过程中产生很多需要储存的气体，由此大容量储气柜得到越来越广泛的应用。储气柜顶盖常采用网壳和加劲壳，其属于大跨类壳结构，具有高柔的特点，对竖向地震作用敏感。郭小农等[1-2]认为矢跨比是影响铝合金板式节点网壳结构基频的主要因素；聂桂波等[3]认为单层球面网壳结构的频率较为密集，外界环境噪声对其频率的影响较大；李峰等[4]认为支座约束对结构自振频率影响较小，矢跨比与网壳厚度的影响较大；李可娜等[5]认为矢跨比对弦支穹顶结构的自振频率影响最大；Shen等[6]分析了矢跨比、截面尺寸等对单层柱面网壳结构动力响应的影响，并提出了一种修正的地震力系数法；吴长等[7]对单层球面网壳在冲击荷载下的动力响应进行了试验研究，结果表明随着环梁刚度增大，结构的动力响应减小；Choi等[8]采用能量方程通过瑞雷能量法得到了非匀质球壳的自振频率；Tatemichi等[9]对全尺寸薄壁穹顶结构进行了动力特性测试，结果表明该结构对竖向振动较为敏感；Lam等[10]采用快速贝叶斯FFT法快速有效地识别了模态参数的最可能值，该法是评估模态参数的重要工具。肋环形加劲浅球壳结构中，球壳与经向肋和环向肋形成的骨架共同受力，其承载力优于光壳和网壳结构。本课题组对肋环形加劲浅球壳结构的静力学性能进行了研究[11-12]，但对其抗震性能方面的研究较少涉及。鉴于此，文中采用模态试验与有限元分析的方法研究矢跨比、支座约束及顶壳厚度对肋环形加劲浅球壳结构自振特性的影响，探讨该结构的动力特性，所得结论可供类似工程设计参考。

1 模态试验

1.1 试验模型的制作

某圆筒型气柜顶盖的结构形式为肋环形加劲浅球壳(见图1)，直径45 m，曲率半径58.5 m，矢跨比1∶10。肋环形加劲浅球壳主骨架由型钢构成，顶壳为6 mm 的钢板拼接而成，材料均为Q235。主骨架中，24根经向主肋截面为槽钢[18a，经向次肋为角钢L75，7道环向主肋截面由内至外为槽钢[16a和[18a，内环梁与支座环梁为刚度较大的H形焊接截面。顶壳与骨架采用连续焊缝连接，经向主肋和环向主肋采用安装螺栓和现场焊缝连接。

图1 某圆筒形气柜顶盖结构Fig.1 Top cover structure of a cylindrical gasholder

根据实际顶盖结构设计两个1/15的肋环形浅球壳缩尺模型，两个模型除顶壳厚度不同外，骨架结构均相同，并忽略经向次肋。0.3 mm厚顶壳的模型为模型1，0.5 mm厚顶壳的的模型为模型2。模型仅在顶壳厚度上有区别，故文中仅展示模型1的具体结构，如图2。

图2 缩尺模型Fig.2 Scale model

模型曲率半径为3.9 m，跨度为3 m，矢高为0.3 m。内环梁为圆管，截面形状为矩形(厚8 mm，高30 mm)，外环梁为L型截面(板厚8 mm，竖板高100 mm，环板宽50 mm)，经向肋与环向肋为下扣的槽型截面(截面尺寸为10 mm×5 mm×0.5 mm)。实际工程中，顶壳与骨架宜采用连续焊缝连接，但缩尺模型的顶壳与骨架厚度较小，若采用连续焊缝将产生较大的变形且易焊穿顶壳，因此骨架之间以及顶壳与经向肋、内外环肋之间的连接均采用点焊，焊点间距20 mm；顶壳与环向肋之间采用铆钉连接，铆钉直径3 mm，间距25 mm。

1.2 试验结果与分析

将模型置于4个橡胶充气膜支座上模拟无约束状态，采用锤击方式对缩尺模型实施单点激励，采用拾振器采集各节点的振动衰减反应。将模型的测点依次编号为1～216 个节点号，见图3，锤击点为216 号节点。采用12 个加速度振动传感器测量模型各测点的加速度，将传感器布置在内环梁1，3，5，7，9，11，13，15，17，19，21，23号节点处，测量完毕依次移动传感器至2，4，6，8，10，12，14，16，18，20，22，24号节点处，再由内向外移动传感器至7道环肋和外环梁上，分18个批次进行测量。

每批次测试均锤击3次第216号节点，并采集各测点的加速度响应数据。应用DASP V10软件对采集的测点加速度响应数据进行Fourier变换，得各测点的自功率谱，再对其进行频率识别。选取模型1第194 号测点、模型2 第212 号测点的自功率谱如图4。

图3 缩尺模型的节点编号Fig.3 Node number of the scale model

图4 测点自功率谱Fig.4 Self-power spectrum of measuring point

由各测点自功率谱识别两个模型的自振频率fT1，fT2，其中前5 阶自振频率见表1。由表1 可知：模型的前5阶自振频率分布不密集，各阶振型相对独立；基频较高，表明结构刚度较好。

根据肋环形加劲浅球壳模型在无约束状态下的加速度响应数据生成两模型的前5 阶振型，振型识别可根据互功率谱与自功率谱之比确定，并考虑相位差确定振型，若相位差为0°，则振型位移同向；若相位差为180°，则振型位移反向。模型1和模型2的前5阶振型见图5。由图5可知：两缩尺模型的振型较相似，第1阶振型有4条节线，第2阶振型有6条节线，第3阶振型有8条节线，但由于模型的第5，6环带附近局部振动较明显，所以第3阶振型的节线不明显；第4，5阶振型均呈较明显的局部振动；两缩尺模型结构的起拱度较低，水平方向刚度较高，竖向刚度较低，因此两缩尺模型的前5阶振型均以竖向振动为主。由此表明，肋环形骨架与顶壳构成的加劲壳具明显的浅球壳振动特征。

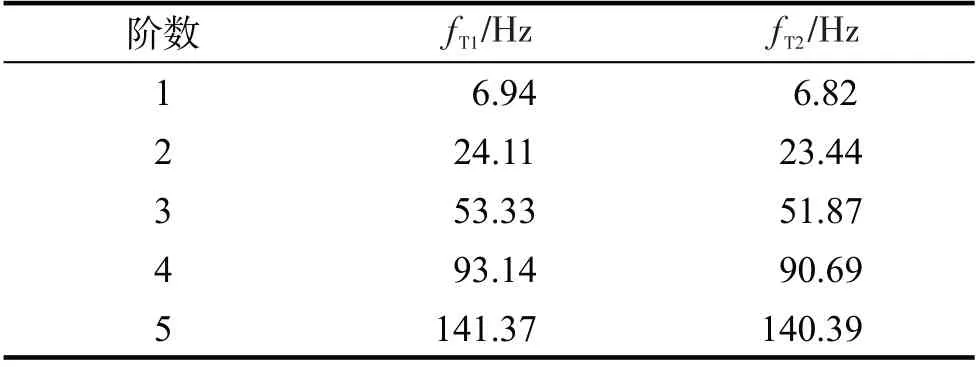
表1 两试验模型前5阶自振频率Tab.1 The first 5 natural frequencies of two test models

图5 两试验模型前5阶振型Fig.5 The first 5 order mode shapes of two test models

2 模态的有限元分析

2.1 有限元分析

根据两缩尺模型的结构和构件尺寸，应用有限元软件ANSYS 建立顶壳厚度为0.3 和0.5 mm 的有限元模型，两模型仅在顶壳厚度上有区别，因此仅展示模型1的有限元模型，如图6。采用beam188单元模拟经向肋与环向肋，采用shell181 单元模拟顶壳。材料为Q235 钢材，密度为7 850 kg/m3，弹性模量为206 GPa，泊松比为0.3。单元与单元之间通过共用节点建模，共9 504个节点，9 360个单元。底部支座处设置为各向无约束。

对两有限元模型进行模态分析，提取各自的自振频率fF1，fF1，前5 阶频率如表2，相应5 阶振型如图7。由表2 可知，两模型的同阶自振频率非常接近，模型1 的自振频率略小于模型2，说明顶壳厚度对自振频率有一定的影响。由图7 可知：两模型的同阶振型相似，第1 阶振型有4 条节线，第2 阶振型有6 条节线，第3 阶振型有8 条节线，第4 振型有10 条节线，第5 阶振型有12 条节线；两模型的振型均以竖向振动为主；无论是低阶振型还是高阶振型，两模型的振型向量最大值均出现在外环梁位置。

对比图5，7可知：前2阶实测振型与有限元模型计算振型吻合；对于第3阶振型，有限元计算得到的振型有8条节线，而实测模型的第5，6环带附近有较大局部振动，节线不明显；对于第4，5阶振型，实测振型显示顶壳局部振动明显。原因在于：缩尺试验模型各构件之间采用的点焊和铆钉连接与有限元模型连续连接有差别；薄壁构件和顶板均存在几何初始缺陷，导致实测过程中难以激发结构的高阶振型；采用的力锤较小，锤击时提供的能量难以激发高阶振型。

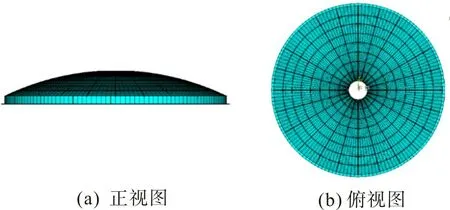
图6 有限元模型Fig.6 Finite element model

表2 两有限元模型前5阶自振频率Tab.2 The first 5 natural frequencies of two finite element models

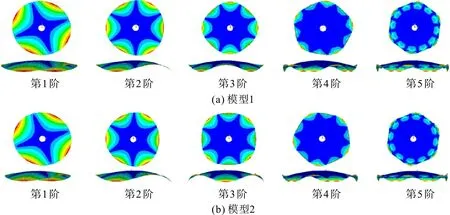
图7 两有限元模型前5阶振型Fig.7 The first 5 order mode shapes of two finite element models

2.2 试验结果与有限元分析结果比较

顶壳厚0.3和0.5 mm试验模型的自振频率实测值与有限元模型计算值见表3。由表3可知，第1阶自振频率的实测值与有限元计算值误差小于5%，其他各阶自振频率的相对误差也均在10%之内，试验结果与有限元计算结果吻合较好，由此表明建立的有限元模型可用于研究肋环形加劲浅球壳的自振特性。

表3 自振频率的实测值与有限元计算值对比Tab.3 Comparison of natural frequency of measured and finite element calculation value

3 自振特性的影响因素分析

采用有限元软件ANSYS分析矢跨比、约束形式、顶盖厚度等对肋环形加劲浅球壳结构自振特性的影响。

3.1 矢跨比的影响

矢跨比是影响浅球壳结构动力特性的重要因素。取有限元模型2，保持跨度为3 m，周边约束为固接，分析矢跨比对浅球壳结构基频的影响，结构矢跨比为1/6，1/7，1/8，1/9，1/10，1/11，1/12，1/13，1/14时，结构基频如图8。由图8 可知，随着矢跨比的减小，肋环形加劲浅球壳结构基频亦减小，即刚度减小。

3.2 支座约束的影响

取模型2，矢跨比为1/10、跨度为3 m、结构约束为周边固接与周边铰接时的前10 阶自振频率见表5。由表5可知，支座约束形式对肋环形加劲浅球壳结构的自振频率影响很小，可忽略不计。

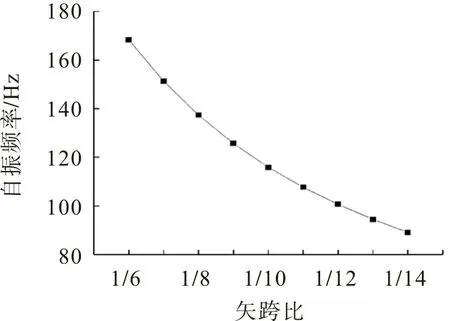
图8 结构基频随矢跨比变化的趋势曲线Fig.8 Variation curve of fundamental frequency with different rise-span ratios

表5 不同约束形式的结构前10阶自振频率Tab.5 The first 10 order natural frequency of structure with different restraints

3.3 顶壳厚度的影响

取模型2，改变顶壳厚度，周边约束为固接状态下的结构基频见图9。由图9可知，顶壳厚度对结构的基频影响较大，厚度从0.5 mm增加到4 mm时，结构基频先增加，之后增加速度逐渐变缓。因此对于肋环形加劲浅球壳，顶壳厚度有一个最佳值。

4 结 论

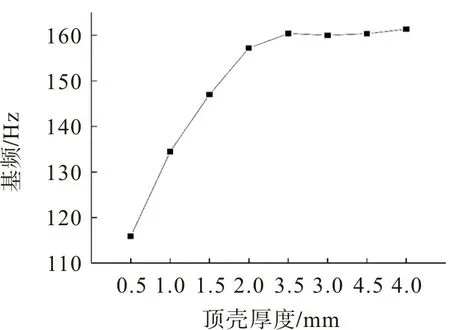
图9 结构基频随顶壳厚度变化的趋势曲线Fig.9 Variation curve of fundamental frequency with top shell thickness

1)肋环形加劲浅球壳结构的基频较高，结构刚度较好，属于刚性结构；结构以竖向振动为主，竖向刚度较弱。

2)对比模态试验结果与有限元分析结果可知，肋环形加劲浅球壳结构前2阶振型吻合较好、高阶振型吻合度较差；结构的前5阶自振频率偏差率均在10%以内，表明采用文中建立的有限元模型可用于肋环形加劲浅球壳结构自振特性分析。

3)有限元分析结果表明：肋环形加劲浅球壳结构的基频随矢跨比的减小而减小；支座约束形式对结构频率影响可忽略；结构基频随顶壳厚度的增加而增加，但增加速度逐渐减小。