固体发射药火炮身管热散失模拟研究

朱 磊,陆 欣

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

火炮发射药燃烧产生的能量除了分配在弹丸做直线和旋转运动外,大量的能量将被身管和弹丸热损失、火药燃气潜热和显热等无用功消耗掉,其中通过身管向外消耗能量占发射药总能量的10%～24%。在内弹道学中无用功常通过减小火药力和增大比热比等隐性方法来求解[1-2]。直接求解身管热散失需要明确火炮身管的温度分布,而火炮身管的温度分布与火炮的身管材料、射击频率、环境温度、换热系数等密切相关[3-7]。火炮身管的热散失将对火炮身管产生烧蚀,长时间将影响火炮的射击精度、首发命中能力和使用寿命[8-10]。

本文以30 mm小口径火炮为例,分析了火炮发射过程中的能量传递方式,使用传热学和内弹道理论明确了传热边界条件,建立计算模型,使用C语言编写程序对单发和连发射击过程中身管热散失的能量进行求解。通过对发射过程中火炮身管的温度场和热散失的研究为火炮身管的烧蚀和弹药保存的安全性提供依据。

1 物理模型

1.1 传热过程描述

火炮发射弹丸需要发射药燃烧产生大量高温、高压、高速流动的火药燃气来推动,这个过程伴随着大量的能量转换与传递。火炮发射过程分为内弹道阶段、后效期、射击间隔期。在内弹道阶段,弹丸在膛内运动,高温高压的火药燃气以极高的速度冲刷着身管内壁,此时内膛处于强制对流换热阶段;在弹丸离开膛口时,膛内的压力仍高于大气压力,火药燃气仍以极高的速度向膛外流动,火药燃气与身管内壁之间为强制对流换热;后效期结束到下一发弹丸发射的时间为射击间隔期,外界的气体进入膛内,与身管内壁进行自然对流换热。在整个身管传热过程中,身管温度沿径向的温度梯度是轴向温度梯度变化的1 000倍以上,因此只考虑径向的温度变化[11-13]。在发射过程中,膛内的火药燃气处于高温高压状态,且燃气的密度较高,具有高吸收系数,火药燃气辐射出的能量在抵达身管内壁之前已经被火药燃气吸收,因此传热忽略辐射所损耗的热量。

1.2 内弹道模型

1)基本假设。

①发射药燃烧遵循几何燃烧定律;

②弹丸摩擦、旋转、后坐等用次要功系数φ来修正;

③火药气体遵循诺贝尔-阿贝尔状态方程;

④假设弹带挤进膛线是瞬间完成的,以挤进压力p0表示弹丸的启动条件。

⑤发射药燃烧产生的能量为定值;

⑥使用火药力和比热比来修正热散失;

⑦膛内密封良好,不漏气。

2)内弹道方程组。

(1)

(2)

(3)

(4)

(5)

式中:χ,χs,λ,λs,μ为火药形状特征量;ψ为发射药已燃百分数;Z,Zk为发射药已燃相对厚度;u1为燃速系数;2e1为弧厚;v为弹丸速度;m为弹丸质量;f为火药力;mp为发射药质量;θ=k-1,k为绝热指数;S为炮膛横断面积。

1.3 身管传热模型

1)基本假设。

①火炮发射时身管内轴向温度梯度远小于径向温度梯度,故仅考虑身管一维径向传热效应;

②忽略火药燃气与膛壁的辐射换热。

2)控制方程。

三维身管导热微分方程:

(6)

式中:φ为柱坐标中任一点在xOy平面上投影与x轴的夹角。

根据假设可将火炮身管传热的控制方程简化为

(7)

式中:a=λ/(ρc),a为身管材料的导温系数,λ为身管热传导系数,ρ为身管密度,c为比热容;r为身管的半径,且r0≤r≤r1,其中,r0,r分别为火炮身管的内、外半径。

3)定解条件。

① 初始条件。

单发:T=T0,T0为环境温度,本文取T0=293 K。

连发:T=T(r),为上一发结束后,后一发初始时刻身管的温度。

② 边界条件。

内边界:

(8)

外边界:

(9)

式中:λ为身管的传热系数;h0,h1分别为火药燃气与身管内壁的强制对流换热系数和空气与身管外壁自然对流的换热系数;T,T0,Tg分别为身管内壁温度、环境温度和火药燃气温度。

2 传热简化模型

2.1 火药燃气温度

由内弹道方程组可以求得内弹道诸元。

1)内弹道阶段。

由能量守恒和内弹道知识可得:

Tv=f/R

(10)

内弹道时期膛内火药燃气的平均温度为

Tg=Tv-(θφmv2/2)/(mpR)

(11)

式中:Tv为发射药燃烧时产生的爆温,R为火药气体常数。

2)后效期阶段。

火药燃气的平均温度为[14]

Tg=Tvexp(-AtB)

(12)

式中:A,B为实验所得拟合指数,有

式中:Tk为内弹道结束时火药燃气的平均温度,Ta为后效期结束时火药燃气的平均温度,tn为内弹道持续时间,th为后效期持续时间。

2.2 换热系数

为了明确边界条件,需要求出内、外边界的换热系数,根据火炮的发射过程中不同时期火药燃气的流动状态和身管外壁实际的换热情况,使用合适的拟合公式来求取换热系数。

1)内弹道时期内边界。

内弹道时期膛内火药燃气处于旺盛的湍流状态,根据马蒙托夫假定和牛顿冷却公式,可推导出内弹道时期换热系数h0:h0=γρg,其中γ为火药燃气的比热比,火药燃气γ的取值范围为0.21～0.42 kW·m·kg-1·K-1,本文选取γ=0.3;其中ρg为火药燃气的密度,可根据公式p(1/ρg-α)=RT求得。

2)后效期阶段内边界。

后效期阶段膛内压力仍大于大气压力,火药燃气高速喷出膛外,此时膛内处于湍流,选取湍流关联式[15]:

Nu=0.08Re0.8Pr0.4,h0=Nu·λ/d0

式中:d0为身管内径。

3)发射间隔期内边界和外边界。

由于发射间隔期膛内处于自然对流,外边界身管由空气自然冷却,因此选取相同的自然对流关联式:Nu=0.52(Gr·Pr)0.25,h0=Nu·λ/d0,h1=Nu·λ/d1,d1为身管外径,h1为外边界换热系数。

2.3 方程离散

内节点的差分方程为

(13)

内边界:

(14)

外边界:

(15)

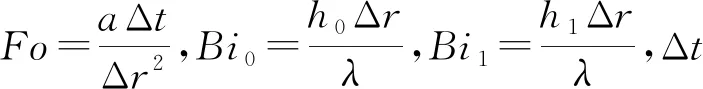
2.4 能量方程

内弹道时期火药燃气的温度比身管内壁的温度高,火药燃气通过身管向外传递能量。在后效期阶段火药燃气温度有一部分比身管内壁温度高,此时向身管传递热量;还有一段时间火药燃气的温度比身管壁温度低,此时身管向火药燃气传递热量达到冷却的目的。身管内壁的热量通过导热的方式向外壁传递。

假设内弹道时期的时间为t1,内弹道结束到后效期阶段火药燃气比身管壁温度高的时间为t2,整个射击时间为t。

内弹道和后效期火药气体与身管内壁的热流密度q0,q1,以及通过身管导热的热流密度qd分别为

q0=h0(Tg-T)

(16)

q1=h1(Tg-T)

(17)

(18)

火炮的身管热散失包括对流和导热两部分,则火药燃气通过身管壁向外传递的热量为

(19)

式中:S1为火药燃气与身管内壁的接触面积。

3 计算结果

为了研究通过身管的热损失,首先要研究身管的温度分布问题。根据上述模型,以30 mm小口径火炮为例,表1给出了内弹道初始参数计算火药燃气的温度。

表1 30 mm火炮内弹道初始参数

火炮的发射过程非常短暂,由图1可知,从发射到后效期结束时间为7 ms左右,火药燃气迅速升高至2 600 K。在内弹道阶段结束时,火药燃气降低到1 500 K,在后效期结束时火药燃气的温度急剧下降到350 K。

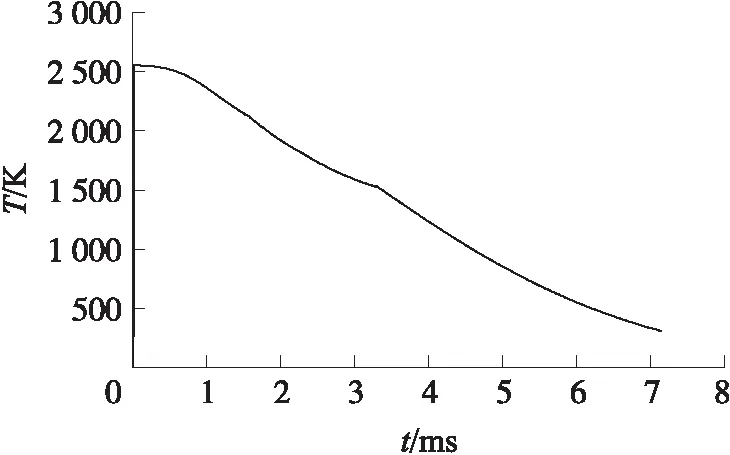
图1 火药燃气温度

表2为身管材料属性。

表2 身管材料属性

图2为3种不同网格情况下距离身管内壁1.4 mm处身管温度随时间变化情况,其中K为身管径向网格数。由图可见网格数K=350和K=500的身管温度分布几乎没有差异,本文选取网格数K=350,网格尺寸为0.1 mm,可以提高计算速度。

单发射击情况下身管的温度分布如图3所示。由图3可知,身管内壁在火药燃气的高速流动下进行对流换热,内壁温度升高到1 046 K,达到最高温度后通过身管向身管内部导热,在1 s时温度下降到421 K。

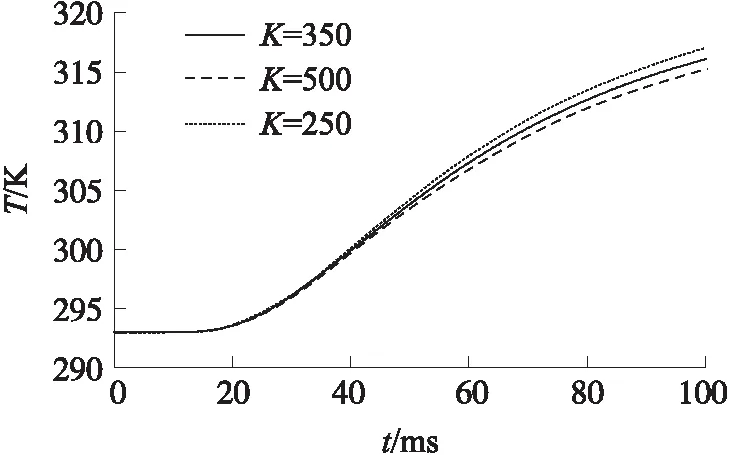
图2 不同网格数时距内壁1.4 mm处温度分布

图3 单发射击身管内壁温度分布

图4和图5分别为单发射击身管径向温度分布和身管三维温度分布。由图可知,沿着径向身管,温度在5 mm左右有变化,即在短时间内,火药燃气传递给身管的能量积蓄在身管的内部。单发射击火药燃气和身管内壁温度如图6所示。由图6可以得到,在内弹道和后效期的一部分时间内火药燃气向身管内壁传递内能,有一段时间火药燃气温度将低于内壁温度,达到冷却身管的作用。

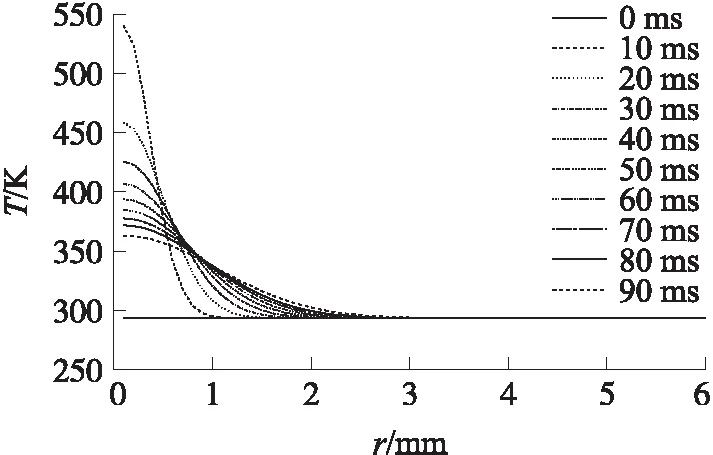
图4 单发射击不同时间情况下身管径向温度分布

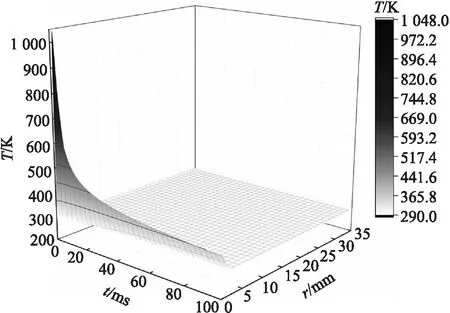
图5 单发射击身管三维温度分布

图6 单发射击火药燃气和身管内壁温度

在研究单发的基础上,对火炮进行10连发射击,射击的频率为600 min-1,结果如图7、图8所示。由图7和图8可以看出:身管内壁的温度与单发的升高趋势相同,并且具有周期性的升高和下降;相比单发,身管的内壁最高温度随着射击数的增加而增加,达到1 228 K,同时身管内壁的最低温度也随着发数的增加而增加到584 K。由连发射击身管温度分布三维图可以看出,随着时间的增加身管的温度和内壁温度一样都具有周期性的升高和下降,身管的温度从内壁到外壁呈下降趋势,而身管的温度只在10 mm范围内有变化,在短时间内,由于身管材料存在热阻,火药燃气传递给身管的热量积蓄在身管的内表面附近。

火药燃气向身管的热散失有对流、导热和辐射,由于辐射的热量都被火药燃气吸收,只考虑了对流和导热。由于身管武器的口径存在差异,身管的热散失也存在差异,其中身管热散失占发射药的总能量在10%～24%之间。在对火炮单发射击后内弹道、后效期和发射间隔期的身管温度分布进行研究的基础上,研究了火炮连发射击后身管的温度分布情况。由表3身管热散失可以看到:首发射击后身管热散失占发射药总能量的比例η=16.45%;随着射击数的增加,热散失占总能量的比例在降低,在第10发时热散失的占比降为13.81%。对表3的数据进行非线性拟合,得到热散失Q和射击数M之间的关系:Q=26.518 69M-0.075 52,与计算数据相比,线性相关度为0.991 37。分析认为,射击的频率较快,时间太短,火药燃气通过身管传递的热量聚集在身管内部,同时身管内壁与火药燃气的温差随着射击数的增加而减小,导致通过身管热散失消耗的能量降低。

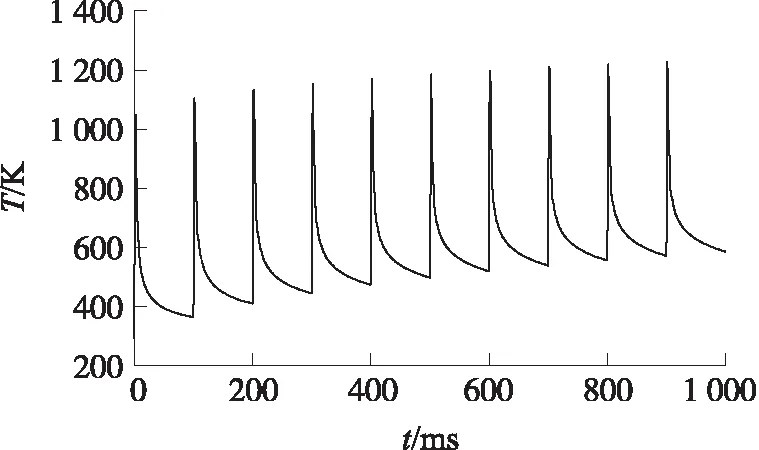
图7 连发射击身管内壁温度

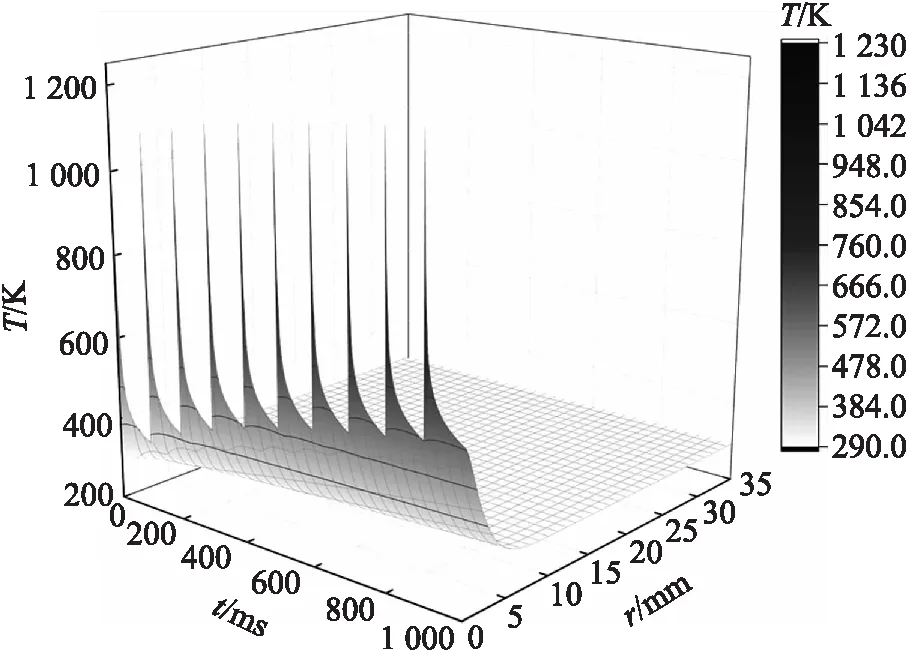
图8 连发射击身管三维温度分布

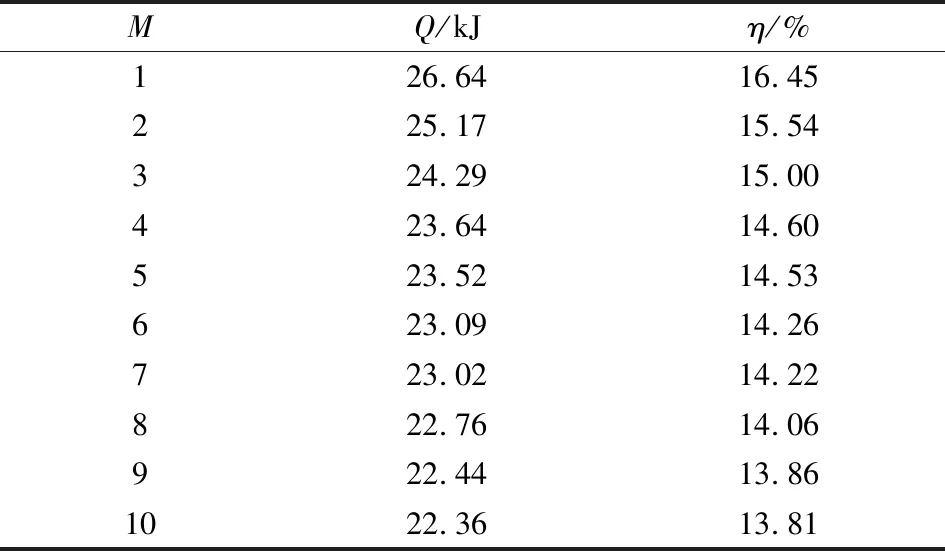
表3 连发射击身管热散失

4 结论

本文从理论上研究了火炮发射过程中的热散失,使用C语言编写程序计算了火炮发射过程中的温度场分布、火药燃气通过身管热散失消耗的能量,得出以下结论:

①单发射击工况下,身管内壁温度在短时间内迅速升高到1 046 K,然后热量向内壁传递导致温度下降到421 K;在连发射击情况下,身管内壁的温度升高和下降具有周期性,每一发射击时身管内壁所达到的最高温度和最低温度都比前一发的温度高。

②身管的整个温度场由内到外温度逐渐下降,在5～10 mm范围内有较大的温度梯度,表明热量聚集在身管的内壁附近。

③在十连发射击情况下,身管热散失占发射药总能量在13.81%～16.45%,后一发的热散失较上一发呈下降趋势,计算结果符合文献[1]中身管热散失占总能量10%～24%的结果。