重力输液器用作泵用输液器的输液精度影响

薛燕彬，高晶敏

（北京信息科技大学 自动化学院，北京 100192）

当前，在使用输液泵挤压输液器进行特殊药物输液的临床治疗中，输液精度引发的输液安全问题越来越被重视[1-3]，如急救药物（纳洛酮、善宁、醋酸奥曲肽等）、麻醉药物（氯胺酮、异丙酚、依托咪酯等）、化疗药物（阿片类药、止吐类药、皮质激素类药等）等药物的高精度静脉输液[4-7]。然而，除了输液泵自身的机械精度外，输液器的材料、弹性、壁厚均匀性、挤压耐疲劳性等也是影响输液精度的重要因素。各品牌输液泵的使用手册均强调了输液器耐疲劳性、壁厚均匀性对流速准确度存在显著的影响，并建议采用与输液泵兼容的泵用输液器。然而泵用输液器高昂的售价阻碍了其普及应用，各级医院使用普通重力输液器替代泵用输液器的现象非常普遍，从而导致输液精度不能可靠保证[8-9]。

近些年，针对重力输液器代替泵用输液器进行高精度、安全输液的研究一直在进行。文[8,10]中，为研究不同输液泵与输液器配合使用、输液泵挤压输液器时间对输液精度的影响，以贝朗Infusomat P 型输液泵和科力建元ZNB -XD输液泵为流速控制装置，以相关医用电气设备国家标准、输液泵对输液器标定标准说明为理论指导，以输液泵流速相对误差公式进行数据处理，对输液器进行试验测试。得出不同种类的输液泵、输液器组合，流速误差不同。同时建议每隔6～8 h 更换一次输液器被挤压位置。文[11]中，重力输液器的材料、弹性、内径等差异直接关系到输液泵的输液精度，并建议应对每一种输液器的流量特性、压力特性、疲劳特性等进行质控。文[12]指出不同溶液因其浓度和黏稠度不同对输液精度会构成影响。

总之，目前的研究指出了输液器耐疲劳性、壁厚均匀性等影响着输液精度，并建议输液前进行输液器标定、输液过程中人工及时更换输液器管路挤压位置等方式去减少输液流速误差过大带来的危害。但是，这些方法欠缺科学的理论指导依据，不能较好地保证输液精度，存在输液风险。

本文研究输液器壁厚偏差、输液器被挤压的耐疲劳性（即输液时间）对输液精度的影响问题，选择双对数模型对输液器壁厚偏差、输液时间、输液精度进行建模；设计了输液器壁厚偏差、输液精度试验系统，并通过对7 种样本输液器进行壁厚偏差、24 h 流速为1 mL/h 的流速测量试验，获得了壁厚偏差、输液时间、输液精度数据；使用所建模型对试验数据进行拟合回归辨识出模型中各项参数，得到了壁厚偏差、输液时间、输液精度回归方程，为标定输液器壁厚不均匀性引起的输液误差提供理论依据。

1 数学模型建立

1.1 输液流速误差因素分析

输液泵主要由微机系统、流量泵、监测装置、报警装置、输入及显示装置组成。流量泵是输液泵的液体动力源，主要通过凸轮轴的转速去控制液体流动速度。当前，指状蠕动泵是目前输液泵主流的液体动力泵结构[13]。指状蠕动泵挤压状态示意图如图1 所示。

图1 指状蠕动泵挤压状态示意图

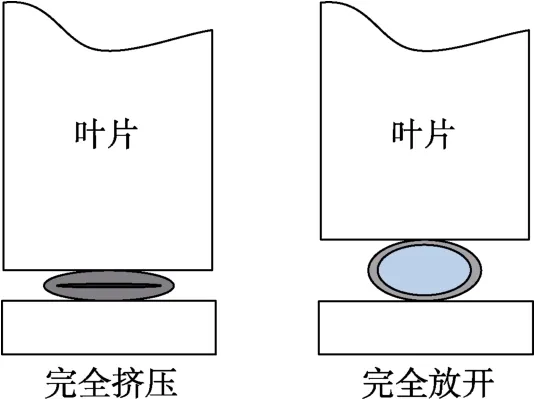
图2 叶片挤压输液管路示意图

如图1 所示，指状蠕动泵的凸轮轴由具有一定间隔的多个凸轮组成，其中各凸轮在轴线上都相差设定的角度。当步进电机驱动凸轮旋转时，凸轮驱使叶片按照一定顺序和规律垂直往复运动，如同波浪一样依次挤压输液器管路（如叶片挤压输液管路示意图2 所示），使输液器管路中的液体以一定的速度定向流动。

由图1 和2 分析可知，每一个叶片都会不断地对输液管路的同一位置进行垂直往复运动，随着时间的延长，输液管路的弹性容易被叶片损坏，使得管路不能恢复原有的管径，再次挤压时产生的形变不同，从而导致流速产生偏差（即输液器管路被挤压时间影响着输液精度）。

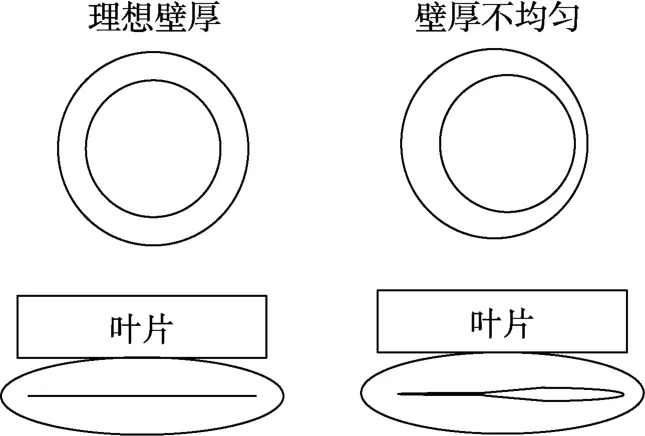
图3 理想壁厚与壁厚不均匀时输液器管路挤压效果图

由图3 分析可知，由于壁厚偏差的存在，在实际挤压输液器管路过程中，并不能完全挤压，总会存在相应的间隙，从而会有相应的流速偏差（即输液器壁厚偏差大小影响着输液精度）。因此，研究输液器壁厚偏差、输液时间与输液精度之间的关系，就必须进行数学建模。

1.2 输液精度模型建立

由 1.1 节分析可知，输液器壁厚偏差与输液时间是决定输液流速误差的重要因素。当前建立的多元回归模型有多元线性回归模型、多元非线性回归模型 2种。考虑到输液器管路在不同时间下实际挤压过程中的形变的非线性变化，将多元非线性双对数模型作为壁厚偏差、输液时间、输液流速误差之间的数学模型，如式（1）所示：

式（1）中，t、x分别代表输液时间、输液器壁厚偏差，y代表输液流速误差，a、b为系数，K为常数。

图4 输液精度模型建立与验证过程

本文模型建立与验证过程如图4 所示：（1）分析输液精度影响因素，并以此建立输液精度双对数数学模型[14-15]；（2）为辨识所建模型中的参数，设计了壁厚偏差测量、时间-输液精度测试试验系统，并通过试验获得了样本数据[16]；（3）将所有样本试验数据分为2 部分，一部分样本试验数据作为训练集，用于所建模型的参数辨识，得出回归方程式。同时，利用回归方程与试验数据分析壁厚偏差与输液精度、时间-输液精度之间的变化关系，另一部分样本试验数据作为测试集，通过模型回归方程的预测值与测试集实测值进行相对误差分析，从而验证模型的有效性、准确性。

2 试验系统及数据获取

为所建模型进行参数辨识提供壁厚偏差、输液精度测试数据，需设计2 个试验系统对样本输液器进行壁厚偏差、输液精度试验。

2.1 壁厚偏差测量试验系统

图5 是输液器壁厚测量专用设备实物图，为获取高精度的输液器壁厚偏差试验数据，采用二次元影像测量仪SMV2010（精度优于5 μm）对输液器管路横截面切段进行参数测量。其中，图5 左上角的铜板由36 个不同尺寸的空心圆桶构成，待测输液管片段插入尺寸合适的空心圆桶中进行固定，便于进行壁厚偏差参数测量。图5 右上角的黑色圆环是输液管片段的横截面影像。

图5 输液器壁厚测量专用设备实物图

2.1.1 试验方法

1）壁厚偏差参数测量试验标定。

为保证测量数据的高精度、可靠性，在进行壁厚偏差测量前需对二次元影像测量仪进行校准。本试验采用德卡精密量仪有限公司提供的校准方法对影像测量仪SMV2010 进行标定。

2）壁厚偏差参数测量方法。

在输液器管路上，每30 cm 取一段高度为0.5 cm的输液管片段，共取 4 段，利用 SMV2010 影像测量仪对每一个输液管片段的横截面外径、内径、圆心距进行测量。其中，为体现输液器管路的整体性，取平均壁厚偏差作为输液器壁厚偏差的衡量参数（平均壁厚偏差为4 个片段的壁厚偏差的平均值）。

3）壁厚偏差参数计算公式。

如图6 所示，输液管路壁厚不均匀主要是指在同一截面上壁厚最薄点、最厚点与名义壁厚偏差较大的现象, 其中图6(a)为壁厚均匀的输液管，而图6(b) 则出现Smax与Smin，即壁厚不均问题。

图6 壁厚均匀性示意图

壁厚偏差计算公式如下：

式中，Smax为输液管路截面上壁厚的最大尺寸,Smin为输液管路截面上壁厚的最小尺寸。

4）壁厚偏差参数测量试验步骤。

测量开始前，需获取4 个输液管片段，并将4 个片段插入尺寸合适的铜板空心圆桶中，同时，对二次元影像仪进行标定，有利于提高试验的科学性和可靠性。测试过程中，首先需调整合适的二次元影像测量仪光照强度、待测片段位置，便于进行输液器片段内外径圆环影像的绘制。其次，通过绘制的圆环，获取输液器内直径、外直径、圆心距等参数。最后，根据壁厚偏差计算公式、方法得到平均壁厚偏差参数。试验步骤详见图7。

图7 壁厚偏差参数测量试验流程

2.1.2 试验数据

输液器样本1、2 的壁厚偏差参数测试试验实物图如图8 所示。壁厚偏差测量数据如表1 所示。

图8 壁厚偏差参数测试试验实物图

2.2 时间-输液精度试验系统

为获得真实、准确的输液器被挤压的时间-流速误差试验数据，需设计一个严谨合理的流速误差测量系统，必须将外在干扰因素（如温度、输液液体受到的压力、液体种类、输液器与输液泵是否标定等）排除。因此，本文输液流速误差试验系统通过将干扰因素设为常数值，将输液壁厚偏差、输液时间作为变量进行试验。输液流速误差试验系统示意图、实物图如图 9和10 所示。

图9 中，加压装置（无油空气压缩机ZWB-36/8）、调压阀（SMC 型BLCH 百灵精密调压阀IR2000-02BG，可设定压强大小）结合使用可以提供稳定的气压（模拟重力输液时药液袋与输液泵之间高度差，本试验气压设定为1.105 个大气压，即模拟药液在1.5 m 进行重力输液），温箱提供恒定温度（试验统一设定为25 ℃），蒸馏水（模拟药液，全部试验均采用同种液体进行输液流速误差测试）在水箱内部压强、输液泵（北京来普LIFEPUM SA5 系列输液泵）蠕动挤压输液器管路的情况下实时地流入分析天平（梅特勒MS304TS 型分析天平，精确到0.000 1 g），同时分析天平将记录的实时数据保存到电脑中。通过图9 设计的输液流速误差试验系统，为下一步进行模型回归、数据分析提供数据支撑。

表1 各样本输液器壁厚偏差测量及其数据处理表

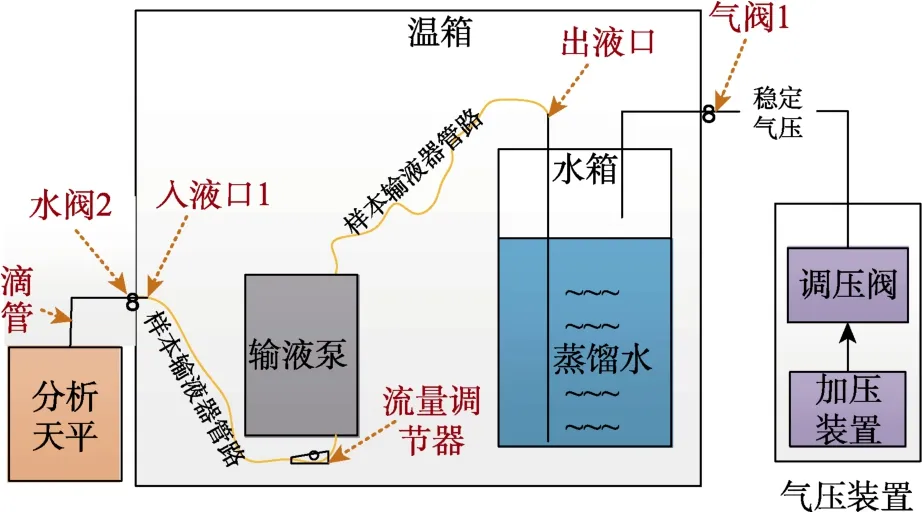
图9 输液流速误差试验系统示意图

图10 输液器流速误差测试试验系统实物图

2.2.1 试验方法

1）输液泵对输液器标定。

根据北京来普惠康医学技术有限公司提供的LIFEPUM SA5 系列输液泵标定方法，在每个时间-输液精度试验开始前对待测输液器进行标定[17]。

2）时间-输液精度测试方法。

使用LIFEPUM SA5 系列输液泵对每个样本输液器进行时间为24 h、流速为1 mL/h 下的输液精度测试。利用梅特勒 MS304TS 型分析天平（可设置数据输出的采样时间）记录并导出输液重量实时数据。

3）时间-流速误差计算公式。

其中，Vsum是从开始计算输液流速到当前时间的总流量是从开始计算输液流速到当前时间的总时间，是实际测量计算出来的流速是设定的流速，Δe是流速误差。

4）时间-输液精度试验步骤。

流速精度试验包含仪器、待测样品输液器、气路、液路等准备阶段和正式测试阶段。其中，仪器准备阶段主要负责各精密仪器的通电、开机、校准等，为试验数据的准确、可靠提供前提；待测样品准备阶段主要负责将待测样品进行处理，使其达到进行试验的要求。气路准备阶段主要负责提供稳定气压，模拟重力输液中吊瓶的高度，保证试验过程中压力的恒定；液路准备阶段负责去除输液管路、滴灌中多余的气泡，杜绝输液泵气泡报警对试验的影响，同时有利于输液流速的准确测量。正式测试阶段负责每个时间间隔获取一次输液数据，并将数据保存在 Excel 表中，便于后期对实时流速、输液误差等参数的计算与分析，如图11 所示。

2.2.2 试验数据

通过输液精度试验系统、试验方法进行时间-输液精度试验，获取时间-输液流速误差数据如表2 所示。

图11 流速精度试验流程

表2 各样本输液器输液误差测量及其数据处理表

表2 中，得到每个输液器样本的时间、流速误差数据，而表1 中，每个输液器样本对应着不同的壁厚偏差。因此，通过表 1、表2 可以进行对壁厚偏差与输液流速误差、时间与输液流速误差的数据分析。

3 模型参数辨识

3.1 试验数据分析

为验证壁厚偏差、输液时间、输液流速误差多变量模型的正确性、有效性，本节在试验数据的基础上，结合所建模型分别从壁厚偏差、输液时间对输液精度影响的角度进行数据分析。

3.1.1 壁厚偏差对输液精度影响分析

为研究壁厚偏差对输液精度的影响，需分析同一时间t的壁厚偏差x与输液流速误差y之间的关系，即把时间t看成常量、壁厚偏差x看成自变量、输液流速误差y看成因变量。因此，可将 1.2 节所建模型中的lnt视为常数。此外，由于为常数，可设常数即壁厚偏差与输液流速误差关系式可化为因此，可通过对试验数据进行回归分析。

将7 种样本输液器壁厚偏差值作为自变量，选择各样本对应的时间t为 9、10、11、12、13、14 h 时（也可以取其他特定时间）的输液流速误差数据作为因变量，并进行回归分析。壁厚偏差对输液精度影响回归分析结果如表3 所示。

表3 输液器管路壁厚偏差对输液精度影响回归分析结果表

其中，第14 h 壁厚偏差与输液精度单变量拟合曲线图如图 12 所示（曲线为拟合曲线，点为实测值）。

3.1.2 输液时间对输液精度影响分析

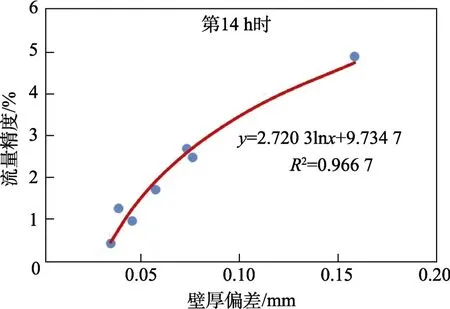
图12 壁厚偏差与输液精度单变量拟合曲线图

为研究输液时间对输液精度的影响，需分析同一壁厚偏差x的样本输液器的输液时间t与输液流速误差y之间的关系，即把壁厚偏差x看成常量、时间t看成自变量、输液流速误差y看成因变量。因此，可将1.2 节所建模型中的 lnx视为常数。此外，由于b、K为常数，可设常数即壁厚偏差与输液流速误差关系式可化为c。因此，可通过对试验数据进行回归分析。

将输液时间作为自变量，样本输液器（样本一、二、四、五、七）对应的各时间点的输液流速误差数据作为因变量，并进行回归分析。输液时间对输液精度影响回归分析结果如表4 所示。

表4 输液器管路输液时间与输液精度单变量模型参数辨识表

其中编号为样本七的输液器时间与流速误差曲线如图 13 所示（曲线为拟合曲线，点为 24个流速误差值）。

图13 输液器输液时间与流速误差拟合曲线图

3.2 模型参数辨识与有效性分析

表5 模型 参数辨识结果表

表5 模型 参数辨识结果表

样本源 样本一 样本二 样本四 样本五 样本七参数辨识 0.4419 1.106 3 2.450 5 a=b=K=回归指标结果均方差RMSE 0.378 7= ，相关系数 0.972 9 r=判定系数 2 0.946 6 R = ，卡方系数 hi quare 16.466 6 C-S =

图14 壁厚偏差、输液时间、流速误差模型回归拟合图

此外，由a、b的数值可知，壁厚偏差值比输液时间更能引起输液流速误差的变化。且在图14 中发现，随着壁厚偏差增大、输液时间的延长，输液器的流速误差会越来越大。

3.3 模型预测分析

将剩余样本（样本三、样本六）试验数据作为测试数据，与回归方程预测的数据进行误差分析（详见表6），从而验证模型的预测效果。其中预测值与实测数据的相对误差计算公式为

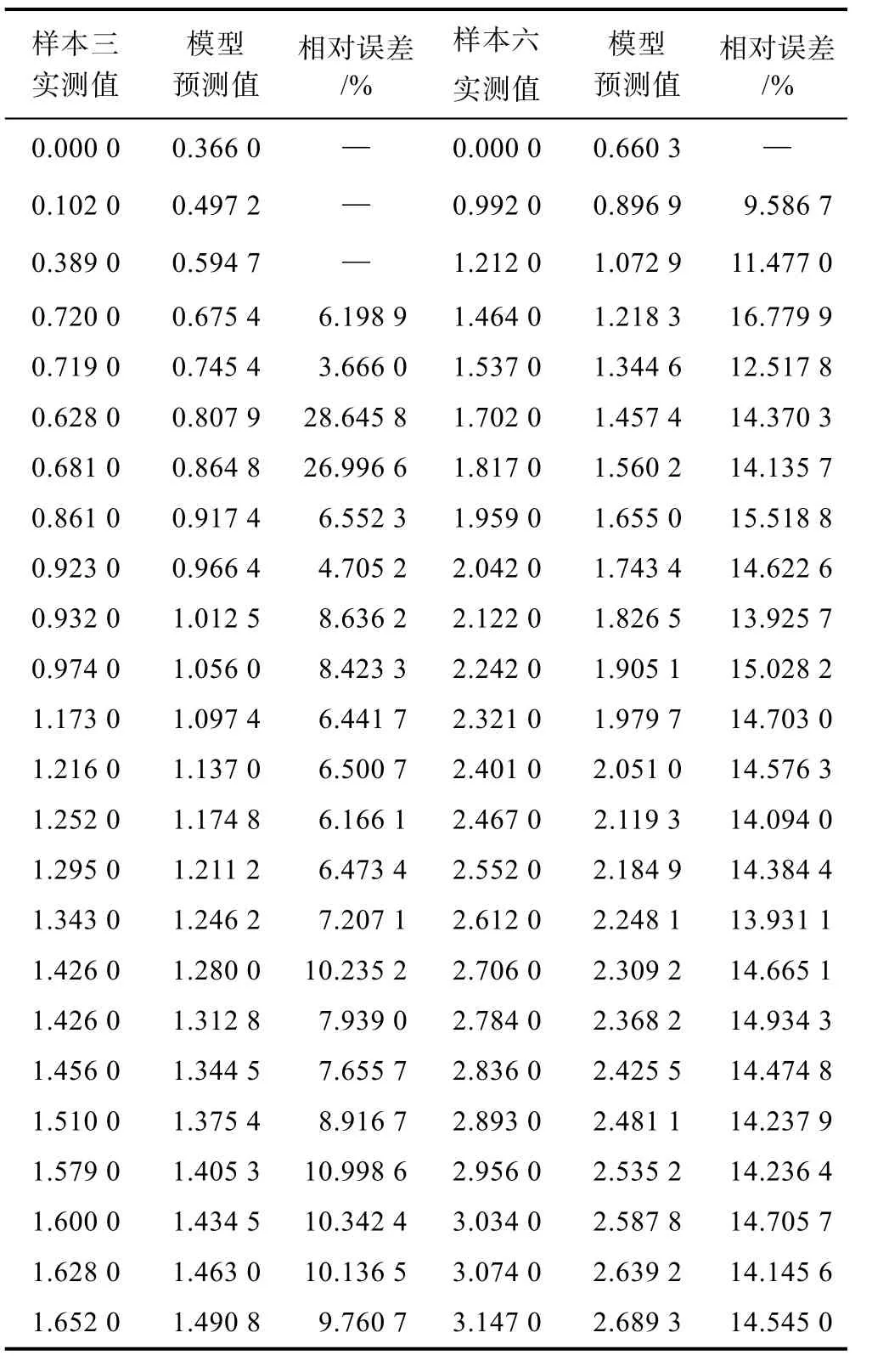
表6 壁厚偏差、输液时间、流速误差模型预测分析表

在表6 中，从壁厚偏差、输液时间、输液精度模型预测值与实测值的相对误差可知，相对误差百分比在10%左右，即模型预测精度高。

3.4 小结

本节首先分析了壁厚偏差、输液时间对输液精度的影响，验证了所建模型既适用于壁厚偏差对输液精度影响单变量分析，也适用于输液时间对输液精度影响单变量分析。其次，利用所建输液精度多变量模型对实测试验数据进行参数辨识。结果表明，该模型拟合优度高达0.946 6，自变量与因变量之间相关性高达0.972 9，且模型可接受概率为0.99，具有正确性、有效性。最后，通过该模型预测值与实测值的相对误差分析可知，该模型具有较高的准确性。

4 结论

本文为验证输液器壁厚不均匀对输液流速误差的影响，设计了壁厚偏差、流速误差测量试验系统，并进行了试验。同时建立了壁厚偏差、输液时间、输液精度多变量模型，并利用该模型对试验数据进行了参数辨识与有效性分析。本文研究结论如下：

（1）输液器壁厚偏差、输液时间是输液流速误差产生的主要原因，壁厚偏差、输液时间越大，输液流速误差也就越大，且壁厚偏差影响更大。

（2）输液器壁厚偏差、输液时间、输液流速误差之间的数学模型为该模型拟合相关系数即自变量（壁厚偏差、输液时间）与因变量（输液精度）之间存在明显相关性。拟合优度很高。此外，该模型卡方系数通过查卡方表可知，该模型接受检验P=0.99，具有正确性、有效性。

（3）当前，由于重力输液器壁厚不均匀，输液泵对重力输液器在标定后仍无法保证输液精度。本文所建壁厚偏差、输液时间、输液精度模型可为标定输液器壁厚不均匀性引起的输液误差提供理论依据。