Miner线性累积损伤理论在滚筒洗衣机轴承寿命计算中的应用

金胜秋 叶超 蒋哲昊

博西华电器（江苏）有限公司 江苏南京 210016

1 引言

轴承是滚筒洗衣机（以下简称洗衣机）的关键零件，其主要作用是：（1）支撑内桶在寿命周期内稳定旋转；（2）动静转承。在洗衣机研发阶段，轴承的选用主要依据便是轴承寿命的计算。因此，采用合理的轴承寿命计算方法对轴承寿命进行预测，在洗衣机研发阶段是非常重要的工作。目前，洗衣机轴承寿命的计算多基于ISO 281中的基本寿命计算公式进行。然而，洗衣机的工作载荷是典型的变幅循环载荷，ISO 281中的计算公式无法直接被应用在洗衣机轴承寿命计算中，需要将洗衣机的变幅循环载荷等效为某一等幅载荷后，再带入公式计算。因此，各个变幅载荷与等效载荷之间的转换对预测轴承寿命十分重要。

2 轴承寿命计算的基础理论

2.1 ISO 281

滚动轴承寿命的传统方法是建立在瑞典科学家伦德贝格和帕姆格伦的滚动接触疲劳理论（L-P理论）基础上的。由国际标准化组织将L-P理论确定为轴承寿命计算的基础，并编入现行ISO 281标准中。

式（1）中：

P——当量动载荷，N；

C——轴承额定动载荷，N；

e——球轴承e=3，滚子轴承e=10/3；

LT——轴承基本寿命，百万转。

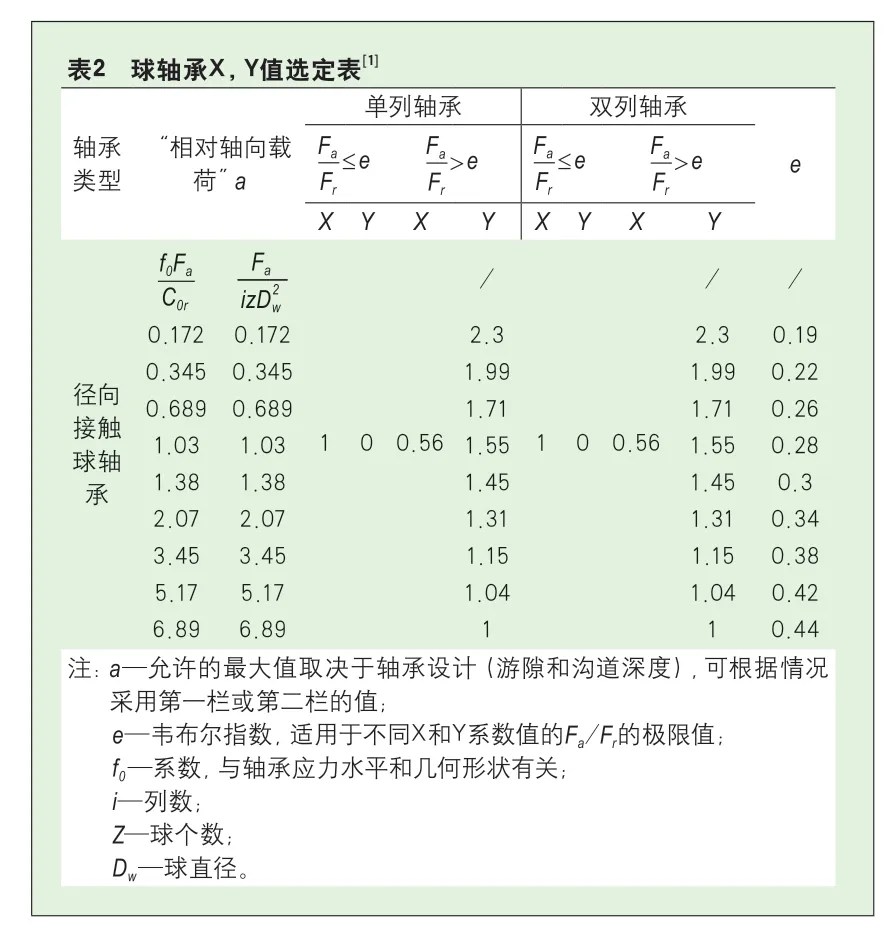
球轴承在工作过程中允许承受一定轴向力，其承受轴向力的能力与承受径向力的能力可以根据ISO 281有如下关系式[1]：

式（2）中：

Fr——径向载荷，N；

Fa——轴向载荷，N；

X——径向载荷贡献系数（可查表）；

Y——轴向载荷贡献系数（可查表）。

2.2 ISO 281在洗衣机轴承寿命计算中的应用

2.2.1 径向载荷Fr

根据滚筒洗衣机的工作原理可知，轴承主要承受径向载荷，简化受力模型如图1所示。

其中：

FAr——大轴承所受径向力，N；

F'Ar——大轴承作用在轴上的力，N；F'Ar=-FAr；

FBr——小轴承所受径向力，N；

F'Br——小轴承作用在轴上的力，N；F'Br=-FBr；

FBelt——皮带作用在轴上的力，N；

FU——偏心负载作用力，N；

FM——含水负载及旋转体自重产生的作用力，N；

M——旋转体质量，kg；

g——重力加速度，m/s2；

L1——轴承间距，mm；

L2——重心至大轴承的距离，mm；

L3——偏心至大轴承的距离，mm；

L4——皮带至小轴承的距离，mm；

R——内桶半径，mm。

洗衣机在工作过程中，主轴相对于轴承外圈，可近似看作围绕轴线的旋转运动，即：径向方向上相对静止。

皮带预紧力Fbelt作用在轴承上的力如图2所示。

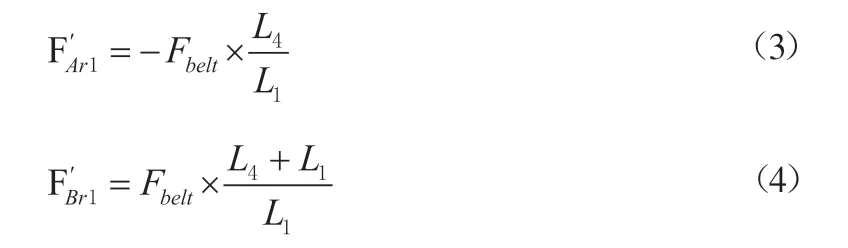
同理：

偏心力FU作用在轴承上的力：

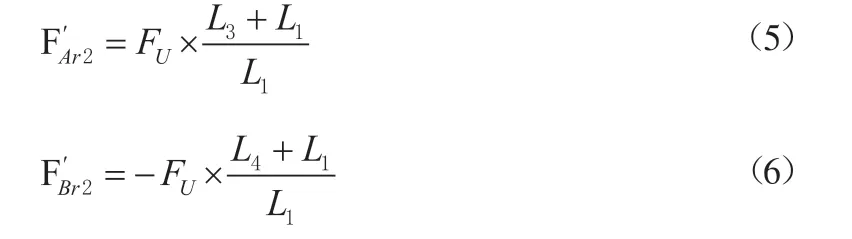
重力FM作用在轴承上的力：

图1 洗衣机简化受力模型

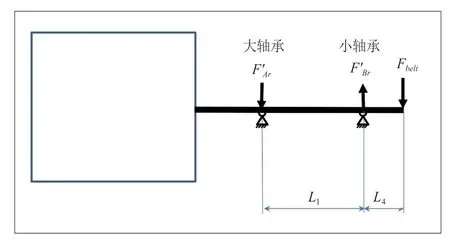
图2 皮带作用力示意图

2.2.2 轴向载荷Fa

对于洗衣机而言，作用在轴承内圈上的轴向力并不是必需的。通常是为了优化轴承的性能，调整轴承游隙，降低轴承噪音而进行设计增加的。根据系统需求不同，轴向力的大小会有差异，市面上也有一些没有对轴承施加轴向力的设计，因此，本文将不对此进行详细说明。

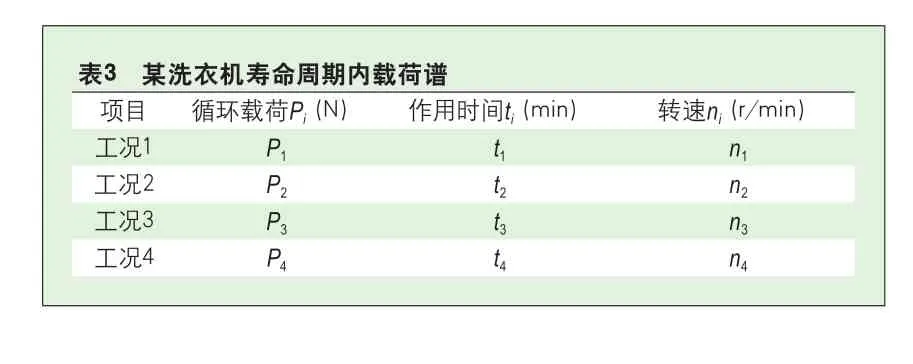
2.2.3 变幅循环载荷Pi

洗衣机在寿命周期内，其工作形式主要分为洗涤、脱水以及烘干（洗干一体机），几种形式往复循环，是典型的交变载荷。某机型工况如表1所示。

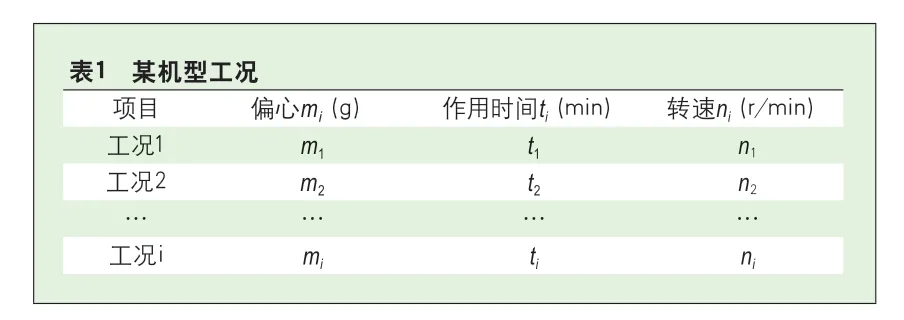
表1 某机型工况项目 偏心mi（g） 作用时间ti（min） 转速ni（r/min）工况1 m1 t1 n1工况2 m2 t2 n2…………工况i mi ti ni

images/BZ_114_582_731_1424_1625.png

images/BZ_114_582_1697_1424_1977.png

根据式（9）和式（10），可得每一个工况下轴承承受的径向力Fri。再根据式（2）有各个工况下轴承承受的循环载荷Pi：

其中，Xi，Yi可根据表2进行选取。

然而，在各个变幅循环载荷对轴承损伤贡献未明的情况下，无法直接应用公式（1）进行轴承基本寿命计算。因此，需要去探索相对合理的加权方法，将各个变幅循环载荷转化为总的当量动载荷，之后再运用公式（1）对轴承寿命进行计算。

3 平均当量动载荷P的计算

如前所述，洗衣机载荷谱由不同工况组成，每种工况对应一个变幅循环载荷Pi，如表3所示。基于受力工况可推知，轴承的损伤主要是疲劳累积造成的。损伤累积规律及损伤准则对于研究此类问题是非常关键的，而疲劳领域里的Miner线性累积损伤理论对这两个问题有很明确的说明。

3.1 Miner线性累积损伤理论

3.1.1 Miner线性累积损伤理论简介

Miner线性累积损伤理论是一种以线性方法来计算累积损伤的理论，其认为：a）在等幅循环载荷作用下，每一个循环对材料的损伤相同；b）在变幅循环载荷作用下，不同幅值的循环载荷对材料的损伤是相对独立的，与加载顺序无关；c）材料临界疲劳损伤为1。

具体的说，Miner理论假设一个循环造成的损伤为：

其中，N为对应载荷作用下的疲劳寿命。

因此，如载荷为等幅载荷，n个循环造成的损伤为：

当载荷由n种变幅载荷构成时，其每个循环包含数量为ki的等幅载荷Si，则1个循环造成的损伤为：

其中，Ni是对应载荷Si作用下的疲劳寿命。

3.1.2 Miner线性累积损伤理论的选用及评价

Miner线性累积损伤理论的成功之处在于大量的实验结果显示临界疲劳损伤的均值确实接近1，在工程上因其便利性被广泛应用，其他确定性方法则需要进行大量实验来拟合众多参数，精度并不比Miner理论更好。并且当零件受到随机载荷作用时，如果随机载荷系列中的疲劳载荷几乎都处于高周疲劳区，用Miner线性疲劳累积损伤理论就足够了[2]。但是，该理论本身也存在局限性：a）未考虑载荷状态对损伤的影响；b）损伤累积过程中未考虑载荷次序的影响；c）未考虑载荷间的相互作用。在应用时应充分考虑上述局限性，必要时需要通过采集大量实验数据进行对比，获得准确的计算精度。特别是对上述局限性敏感的领域，需要考虑进行有针对性的修正。

对洗衣机而言，轴承所承受的随机载荷几乎都分布在高周疲劳区域。因此，选用Miner理论已经足够了。

3.2 Miner理论在洗衣机轴承寿命计算中的应用——平均当量动载荷P

基于Miner理论，对洗衣机受力工况分析如表4所示。

则，轴承运行每转产生的损伤为：

由此，基于ISO 281与Miner线性累积损伤理论，推导出各工况循环负载与总负载的关系式，即平均当量动载荷P的表达式。将该表达式代入公式（1）中，可计算出洗衣机轴承基本寿命。

4 工程应用

目前，应用上述理论指导进行轴承选用，经我司的内部测试表明所选轴承能满足工程需求，技术方案已经在我司多个机型中应用。举例如下：

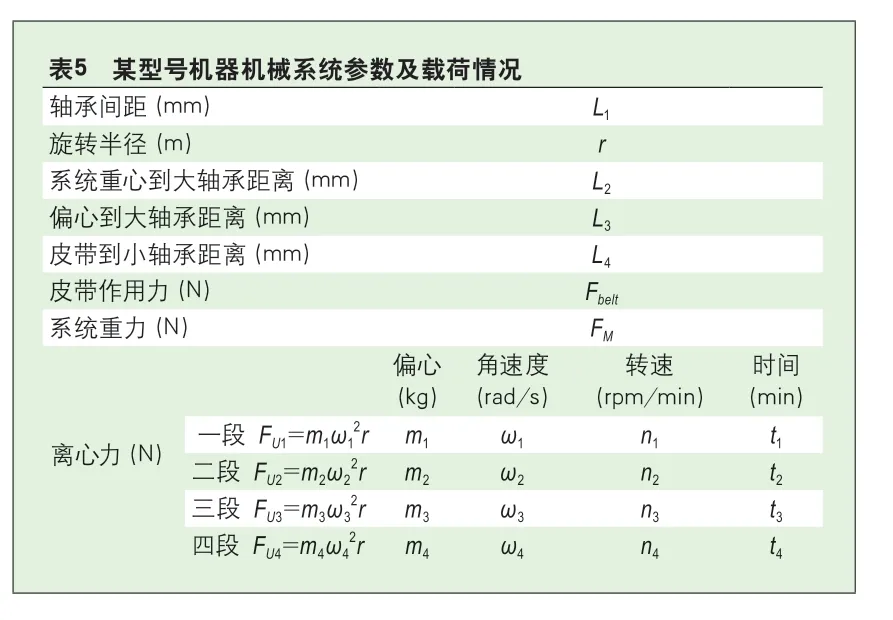
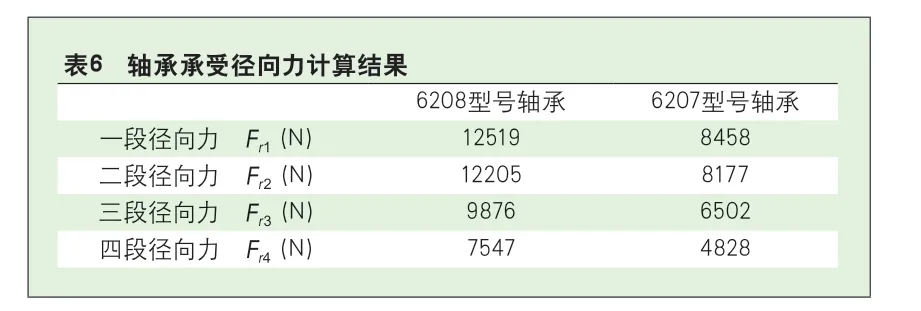
拟为我司某型号机器选用A厂家6208/6207型号的轴承，该机型机械系统参数及受力情况如表5所示。根据式（9）、（10）分别将参数带入，计算结果如表6所示。

该型号洗衣机轴承不承受轴向力，因此，6208型号轴承与6207型号轴承所承受轴向力均为0。根据式（11）有：

将计算结果及相关参数代入式（20）得：

images/BZ_115_1080_379_1922_692.png

images/BZ_115_1080_752_1922_1324.png

images/BZ_115_1080_1383_1922_1663.png

P6208= 9984 N

P6207= 7307 N

查询A厂家6208型号轴承与6207型号轴承的额定动载荷分别为30000 N与26000 N，根据公式（1）有：

6208型号轴承基本寿命：

L10=27.13×106转

6207型号轴承基本寿命：

L10= 45.05×106转

根据载荷谱，其平均转速nA：

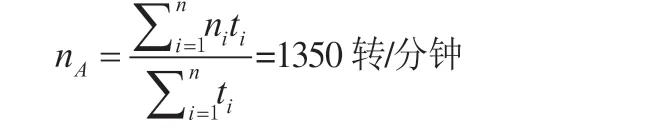
因此，6208型号轴承与6207型号轴承的基本寿命分别为335小时与556小时。

根据ISO 281，对其寿命进行修正计算，计算公式如式（22）[1]：

其中 ：

a1——基于可靠性的寿命修正系数，当可靠性为90%时取1，不同可靠性需求的该值选取详见参考文献[1]，第21页表12；

aISO——基于系统方法的寿命修正系数，详见参考文献[1]，第28页公式（31）～（33）。

基于选择轴承及油脂特性，代入计算可得6208型号轴承修正寿命：

L10m= 742小时

由于同一台机器上配置6208的基本寿命比6207的苛刻，因此针对6208进行理论计算与实验数据对比，如表7所示。

综上，通过对寿命实测值进行统计分析，得到其90%的单侧置信区间下限为609小时，即轴承在该载荷谱作用下，其工作时长达到609小时以上的概率为90%。根据理论计算，同等概率下，其工作时长约为742小时，理论计算与统计值相差18%。该误差需要结合实际情况进行分析：受工程应用时间限制，样本体量受限，统计数据可能存在一些偏差；根据我司多个机型的测试与计算结果比对，误差大约分布在15%～25%之间。因此，作为设计初期技术方案的选用依据，结合一定的余量设计，该精度是可以接受的，对早期方案评估及选用有实际意义。

5 结论

基于上述理论研究及应用测试，可得出以下结论：

（1）ISO 281中关于轴承基本寿命计算的理论，可以直接用于计算滚筒洗衣机在变幅载荷作用下的各个阶段变幅循环载荷的计算问题。

（2）对于洗衣机而言，应用Miner理论，在线性疲劳领域建立各个阶段的变幅循环载荷与总当量动载荷之间的关系，对早期方案评估及选用有指导意义，具有工程应用价值。

（3）本文的研究成果可以为其他领域内变幅载荷作用下的轴承寿命计算提供参考。但是当随机载荷分布在低周疲劳区域时，则需要考虑结合实验对其进行修正。