不同轴压比RCS梁柱组合件抗震性能分析

(华侨大学土木工程学院，福建厦门，361021)

钢筋混凝土柱-钢梁(RCS)组合框架结构具有优异的抗震性能，受到国内外学者的广泛关注，其中梁柱节点是形成结构整体的关键部件，但在地震作用下节点受力复杂，极易发生剪切脆性破坏。为解决混凝土柱-钢梁混合框架结构节点处连接问题，国内外学者针对RCS 节点提出不同的构造形式，并进行了大量试验。李贤等[1]提出了一种新型端板高强螺栓连接的狗骨式削弱钢梁-钢筋混凝土柱节点，并采用拟静力试验证明了此种形式可有效提高节点的刚度与延性；马辉等[2]对型钢再生混凝土柱-钢梁组合框架边节点进行拟静力试验，以轴压比为参数定量分析各项抗震指标，证明了该边节点在不同参数下具有较好的抗震性能；门进杰等[3]在RCS节点处将钢梁翼缘切除，并将腹板贯通混凝土柱，对此种构造形式的节点进行拟静力试验，发现此种构造形式可加强内外混凝土强度，有效提高节点受剪承载力和延性；马宏伟等[4]提出一种梁贯通式的蜂窝组合梁-复合螺旋箍混凝土柱节点，并进行循环加载试验，发现此种节点形式在延性和耗能方面性能优异；KHALOO等[5]以不同形式的刚性面板与剪切键组合，将钢梁与混凝土柱在节点处连接，并通过拟静力试验发现刚性面板及剪切键可有效减少节点处的剪切变形，提高节点抗剪能力；DELIMA 等[6]通过扩展RCS 节点处的端板接头，对不同参数下的RCS 组合件进行了拟静力试验，发现适当拓展端板接头，可有效提高RCS 组合件的抗震性能；BAKHSHAYESH等[7]通过搭接板将钢梁与RC柱在节点处连接，发现此种构造形式可大幅增强组合件的整体性，有效提高其耗能能力。以上这些构造形式虽能一定程度上提高RCS 组合件的抗震性能，但没有具体考虑部件制作、施工操作等成本，严重制约着RCS混合框架结构在实际工程的应用。

鉴于此，本文作者按“强柱弱梁、强节点弱构件”的设计原则，将节点区域复合焊接环式箍筋改为由钢板箍约束，操作简单，降低了设计难度，且钢板箍不仅能有效约束节点处的核心混凝土，提高节点区域的抗剪能力，而且可使节点处形成一个钢质耗能区，大幅提高节点的抗震性能，满足规范的设计要求。同时考虑到在地震作用下，RCS组合结构自身的竖向荷载所引起的二阶效应，往往是结构抗震不可忽略的因素，因此，有必要深入研究轴压比对此种节点构造形式的RCS 梁柱组合件抗震性能的影响，以便于本文研究的RCS梁柱组合件在工程中的应用。本次试验设计了6个比例为1/2 的蜂窝钢梁-RC 柱组合件，并通过ABAQUS 有限元软件进行扩大参数分析，更准确地研究轴压比对其各项抗震指标的影响规律。

1 试验简介

1.1 试验设计与制作

根据文献[8]，试验共设计6 个1/2 缩尺模型的RCS组合件，RC柱上下反弯点距离为1.8 m，蜂窝钢梁反弯点相距2.4 m，组合件分别命名为RCS-N1，RCS-N2，RCS-N3，RCS-N4，RCS-N5 和RCS-N6，试验轴压比设计参数见表1。试件中柱的截面长×宽为200 mm×200 mm，外伸端板长×宽×高分别为300 mm×20 mm×35 mm，蜂窝钢梁的梁高为165 mm，腹板厚度为10 mm，翼缘长为125 mm，厚度为10 mm。

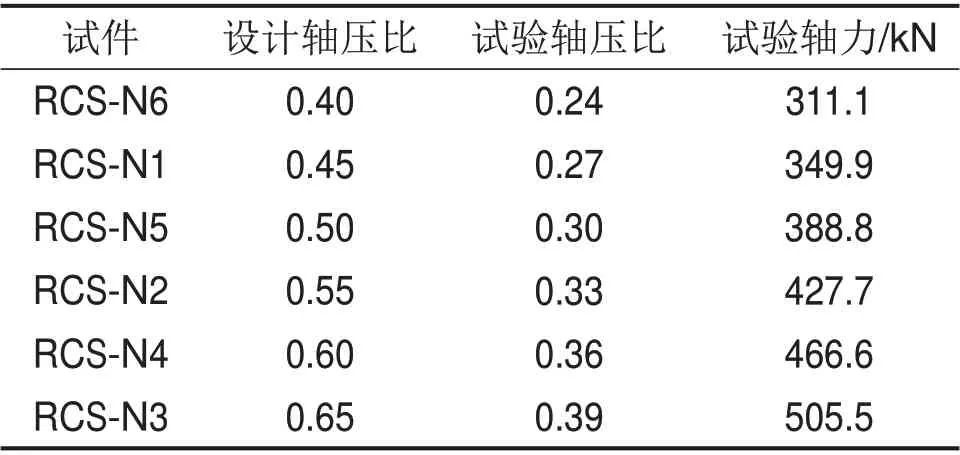
表1 试验设计参数表Table 1 Experimental design parameters

钢板箍作为组合件的核心部件，其尺寸设计应考虑节点处的弯矩和剪力。设计时首先进行节点处的正截面承载力和抗剪承载力验算，分别计算出钢板箍的最小厚度，取两者较大值为钢板箍的厚度；同时根据连接范围内弯矩和剪力的分布确定钢板箍高度。根据计算结果，确定的钢板箍具体参数如下：截面长×宽为200 mm×200 mm，壁厚为8 mm，高度与外伸端板均为350 mm。

本试验中RC柱节点区域采用钢板箍以代替复合环式箍筋，并在钢板箍上下各200 mm 的范围内，对RC 柱箍筋进行加密，具体如图1所示。钢梁与RC柱之间采用10.9级M20高强螺栓连接，防止在循环荷载作用下螺栓过早屈服，出现较大残余变形，影响试验结果。节点处的具体连接形式如图2所示。

制作模型具体步骤为：

1)首先将RC柱纵筋焊接于柱底的钢板上，绑扎箍筋，然后将钢板箍套入试件设计时相应位置并在对应的孔洞上插入栓杆，形成完整的钢筋骨架；

2)浇筑混凝土柱，经养护达到规定强度后拆模；

3)将端板移动至设计位置后焊接上钢梁，在从端板伸出的栓杆上套上螺帽，施加预紧力，为防止节点处各部件由于连接不牢而产生滑移，同时最大程度利用螺栓强度，通过计算[9]，将预紧力设为150 kN。

1.2 材性测试

试验拟配强度等级为C60的混凝土。在每次浇筑的同时，制作3个长×宽×高为150 mm×150 mm×150 mm的立方体混凝土标准试块，经标准养护后，测得的RCS-N1，RCS-N2，PRCC-3，RCS-N4，RCS-N5 和RCS-N6 试件平均混凝土抗压强度fcuk分比 为65.8，66.1，63.8，65.8，66.1 和63.8 MPa。试验所用钢材均采用Q345 钢，钢筋则采用HRB400 热轧钢筋，两者材性测试结果如表2所示。

图1 试件构造及配筋Fig.1 Specimen structure and reinforcement

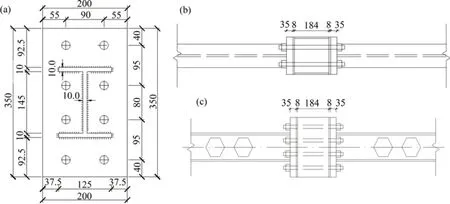
图2 节点处连接构造Fig.2 Connection structure at node

表2 钢材的力学性能Table 2 mechanical properties of steel

1.3 加载装置及加载制度

为保证柱竖向荷载在试验过程中稳定，试验通过可随上部小车滑动的千斤顶施加轴力，并在其前端配置球铰，允许柱顶转动，同时在上柱端施加水平位移，这些设置可有效模拟地震作用下组合件实际受力状态。钢梁端部与设有轴承的梁端拉压杆连接，试件可以左右移动。加载装置如图3所示。由图3可见：通过MTS作动头在柱顶施加水平位移，控制水平力，并按照文献[8]确定位移加载制度。试件屈服前，对每一级位移角进行一次循环；当从MTS 显示屏上观察到某一级滞回环明显增大时，可判断此位移角下试件已屈服，屈服后的位移角进行3次循环，具体加载制度如表3。当组合件水平荷载衰减至最大水平荷载的85%时，终止试验。

图3 加载装置Fig.3 Loading device

表3 加载制度Table 3 Loading program

1.4 测试内容及测点布置

试件测试内容主要包括：柱顶加载点与柱底的水平位移；梁端的弯曲变形、节点区的剪切变形以及钢梁与RC 柱的连接变形；RC 柱纵筋、箍筋、钢梁端部上翼缘、腹板以及钢板箍的应变。测试装置及测点布置如图4所示。

2 试验现象及破坏形态

2.1 试验现象

当试件RCS-N1，RCS-N2，RCS-N3和RCS-N6位移分别达到12.0，17.7，18.0 和11.9 mm 时，钢板箍下部150 mm区域内混凝土开裂，开裂荷载分别为54.9，68.0，69.0和53.8 kN，当继续加载至位移角(幅值)1/75(24.0 mm)时，试件中RC 柱侧裂缝增多并开始向内发展，此外，柱端也开始出现剪切斜裂缝，滞回环较前几次明显变大，此时试件都已屈服，屈服荷载分别为76.0，78.6，84.2 和72.2 kN。随着加载位移不断增大，在加载至位移角(幅值)1/35(51.4 mm)时，试件都已达到峰值荷载，分别为101.8，101.3，103.3 和96.2 kN，当位移分别加载至105.9，100.8，96.7和106.0 mm，此时荷载下降至峰值荷载的85%，分别为83.9，81.3，80.9 和82.2 kN，试件达到极限状态，钢梁蜂窝孔洞开裂严重，不宜继续加载，停止试验。试件破坏形态如图5所示。

当试件RCS-N4 和RCS-N5 位移分别达到17.8和17.7 mm 时，节点核心区下方出现第1 条裂缝，开裂荷载分别为62.0 kN 和61.1 kN，当位移角(幅值)1/75(24.0 mm)加载完毕后，发现滞回环明显增大，此时钢梁已经屈服，屈服荷载分别为86.2 kN和82.5 kN。随着继续加载，当加载位移分别为36.0 mm 和51.3 mm 时，试件达到峰值荷载，分别为94.1 kN 和87.8 kN。当试验进行至1/35(72.0 mm)位移角(幅值)的反向循环时，因焊缝突然开裂，试件RCS-N5 承载力骤降至63.0 kN，可判定试件破坏，遂终止加载，同样试件RCS-N4在正向加载至80.0 mm 时，承载力骤降至64.0 kN，已达到峰值荷载的65%，无法继续承载，停止试验。两者都是由于蜂窝钢梁与端板的连接焊缝断裂导致承载力突降，属于构造破坏。构造破坏形态如图6所示。

图4 测点布置Fig.4 Arrangement of measurement points

图5 钢梁屈曲及蜂窝洞开裂Fig.5 Steel beam buckling and honeycomb hole cracking

图6 钢梁与端板焊缝开裂Fig.6 Cracking of weld seam between steel beam and end plate

2.2 破坏形态分析

试件RCS-N1，RCS-N2，RCS-N3 和RCS-N6发生梁铰破坏，试件RCS-N4 和RCS-N5 发生构造破坏，根据各试件的破坏形式分析可得：

各试件节点由于钢板箍对核心混凝土约束较强，裂缝通常出现在节点上下区域处，且至试验结束，斜裂缝始终没有贯穿整个柱子截面，有效避免了普通RCS 梁柱节点的剪切脆性破坏，实现强节点的框架设计原则。

当试件发生梁铰破坏时，承载力衰减缓慢，延性较好，充分发挥钢梁的耗能作用，相比于梁铰破坏，构造破坏应该是工程应用中极力避免的，一旦发生构造破坏，节点承载力快速下降，抗震性能变差。

3 有限元建模

3.1 材料本构

采用ABAQUS对试验组合件进行有限元分析。混凝土使用塑性损伤本构模型[10]，钢筋和高强螺栓均采用普通双折线模型[11]。对于钢梁来说，试验中承受循环荷载作用，对其材性的定义需考虑随动强化特征，故选用二折线随动强化模型[12]。试验材料参数取自表2和表3。

3.2 单元选取与界面处理

根据模型变形及受力特点，混凝土、高强螺栓和Q345 钢材部件均采用C3D8R 实体单元，HRB400 钢筋采用T3D2 桁架单元；由于本试验组合件由多种材料组成，且在RCS 组合节点处构部件复杂交汇，因此，要有效模拟试件在反复荷载作用下(大位移、大变形并考虑损伤累积的非线性行为)的抗震性能，准确定义节点各部件之间关系是模拟的关键，采用面与面接触来建立各部分之间的接触关系，共建立5个接触对，其中，以螺栓表面与螺帽内侧面为接触面，外伸端板孔洞与外表面为目标面，同时外伸端板内表面与钢板箍外表面建立另一接触对；在试验过程中，并未发现钢板箍与混凝土柱出现滑移分离现象，钢板箍与柱面采用绑定关系；对于高强螺栓与混凝土柱之间，分别对内置、绑定和接触3 种关系进行试算，发现绑定与试验结果最相近，故采用此种方式定义两者关系。

3.3 单元划分与模型建立

选用试件尺寸进行仿真建模，组合件模型见图7(a)，各部件由于孔洞存在，为保证网格质量，先对各个部件进行分区，节点区域划分更细密，以便计算收敛。对于所有实体部件均采用扫略中性轴算法进行网格划分，由ABAQUS 生成相应网格，网格模型见图7(b)。

4 有限元结果验证

为验证有限元分析结果的正确性，以组合件RCS-N1，RCS-N2，RCS-N3 和RCS-N6 的各项参数为基础，建立模型，从滞回曲线、骨架曲线、破坏形态和峰值荷载方面，对比数值分析与试验结果，如图8～9和表4所示。

由图8可见：在循环往复加载过程中，钢梁梁端为主要受力构件且在加载结束后发生较明显的屈曲变形，这与试验结果(梁铰破坏)一致，达到了强柱弱梁的设计目标。由图9可见：模拟的滞回曲线与试验结果相比，刚度退化较试验略低，分析可知钢材本构采用较理想化的双折线随动强化模型，这与实际钢材力学性能有所区别。

由图9(e)～(h)可见：有限元计算的结果正反向荷载较对称，而试验曲线在反向加载时低于正向加载，可能原因为在正向加载过程中，混凝土柱受力两侧产生细微裂缝是不对称的，由于混凝土的力学特性，受拉侧混凝土裂缝更细密，在反向加载过程中，混凝土不可能完全拉压恢复，故导致反向加载时荷载变低，而在有限元分析过程中，柱只发生损伤却不产生裂缝，可进行完全拉压恢复，导致有限元结果正反荷载较为一致。在弹性阶段，RCS 梁柱节点试验骨架曲线较数值模拟来说，加载初始刚度略高，可能因为有限元模拟试件上下柱端都为铰接，而实际试验过程中各部件摩擦的存在，柱端并不完全铰接，表现出一定的刚接性质，导致试验初始刚度略高。

数值模拟峰值荷载与试验结果对比见表5，正向平均误差为4.8%，反向平均误差为10.6%，两者相差不大；在骨架曲线下降段两者强度衰减速率较一致。因此，有限元分析有较高可信度，可以反映组合件在不同参数下的抗震性能。

5 扩大参数分析

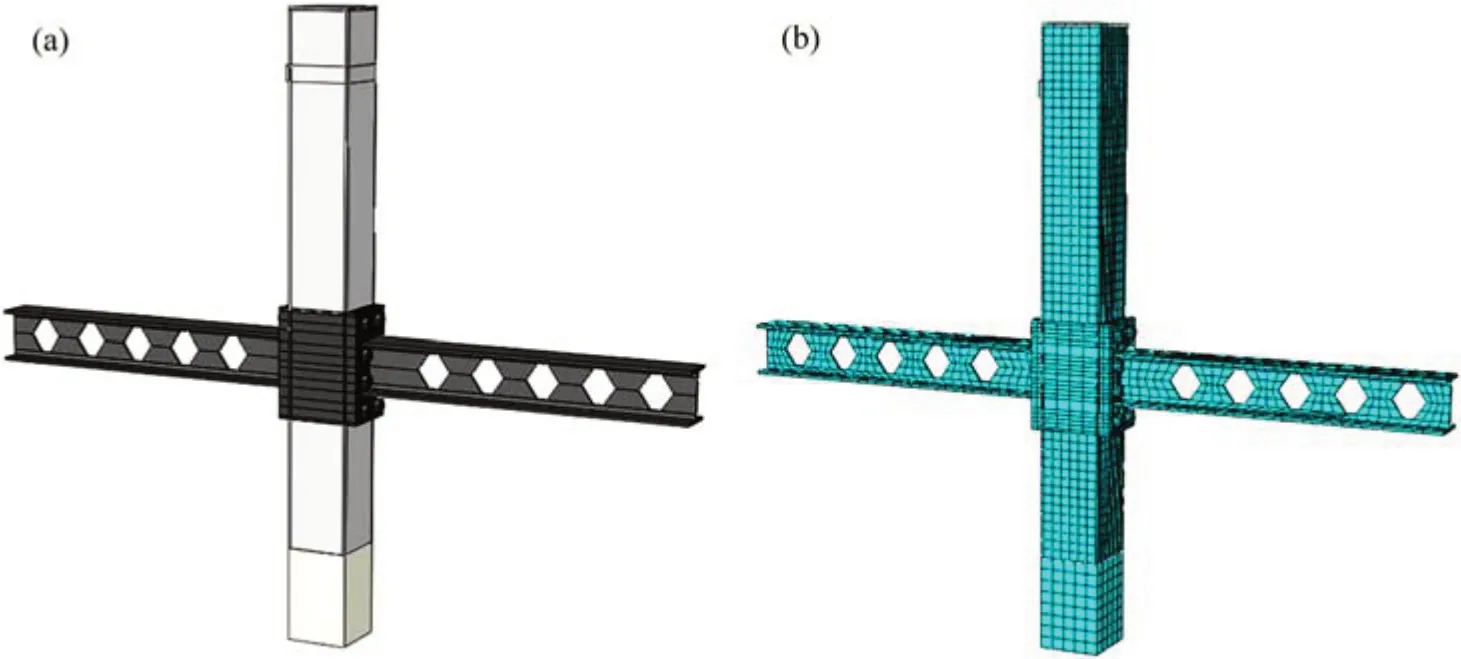
图7 有限元模型Fig.7 Finite element model

图8 破坏形态对比Fig.8 comparison of failure patterns

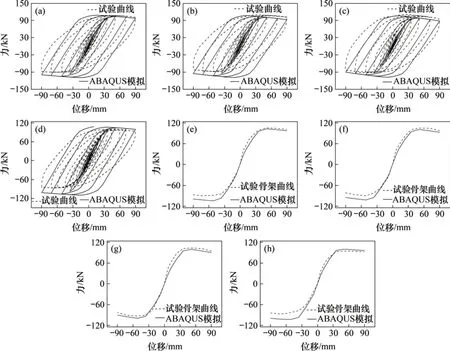
图9 RCS组合件试验与有限元模拟结果对比Fig.9 RCS assemblies test and finite element simulation results

表4 组合件承载力对比分析Table 4 Comparative analysis of bearing capacity of components kN

为保证试验结果与其所得结论的准确性，针对此种新型节点形式的RCS 梁柱组合件，通过ABAQUS软件进行扩大参数分析，以RCS-N1试件尺寸及各项材性实测结果为基础，把轴压比作为研究参数，分析7个有限元模型的抗震性能，组合件参数见表5。组合件模型不存在焊接质量及其他初始缺陷问题，为保证破坏荷载能够达到峰值荷载强度85%，采用位移控制加载制度，将加载级数增大，在现有试验加载位移角之后，再添加1/15(120 mm)位移角(幅值)，但为保持与试验一致，滞回曲线仍取前10级加载。

表5 模型设计参数Table 5 Model design parameters

6 抗震性能分析

6.1 滞回曲线

图10所示为有限元分析RCS 组合件滞回曲线，图11所示为试验RCS 组合件滞回曲线，由图10和11可见：

图10 有限元分析RCS组合件滞回曲线Fig.10 Finite element analysis of hysteresis curve of RCS assemblies

图11 试验RCS组合件滞回曲线Fig.11 Hysteresis curve of test RCS assemblies

1)试件未屈服前，加载与卸载段较为平直，滞回环面积较小，表现较为规则的四边形。试件屈服后，荷载位移曲线开始呈非线性变化，滞回环面积增大，但强度没有明显降低，而刚度退化幅度较大，说明梁铰机制形成，钢梁成为主要受力部件，又因为其良好的耗能能力，导致组合件的滞回曲线十分丰满。

2)对于发生梁铰破坏的试件RCS-N1，RCS-N2，RCS-N3 和RCS-N6 来说，当轴压比增大时，组合件的滞回曲线愈加丰满，原因可能为较高的轴压比限制柱的裂缝开展，减小混凝土柱的损伤，而且高轴压比提高了高强螺栓和钢板箍与柱子的摩擦力，节点区域变得更为刚性，减小滑移，导致滞回曲线表现出更为丰满的梭形。

发生梁铰破坏的试件，其具有十分饱满的滞回曲线，其在延性和耗能等抗震指标上均优于发生构造破坏的试件，钢梁的塑性变形能力得到了充分发挥。

在有限元计算初期，加载与卸载段大致重合，滞回环呈尖梭形；但在试件屈服后，曲线开始偏向位移轴，滞回环增大明显，耗能增强，这与试验结果变化历程一致。总体来说6个构件滞回曲线均呈纺锤形，且轴压比越大，滞回曲线越饱满。

图10和图11相比，两者滞回曲线存在一定的特征差异，除轴压比影响外，另一部分原因可能为在试验中，横向固定栓杆与混凝土孔洞存在着相互作用，在低周反复加载过程中，孔洞处出现一定的应力集中，此处混凝土损伤严重，导致螺栓不能稳定固定在设计位置，存在着一定的滑移，引起试验滞回曲线有一定程度的捏缩与倾斜，而有限元建模时各部件位置较准确，计算过程中由于栓杆与柱之间采用“Tie”命令耦合在一起，节点处各部件协同性较好。

6.2 骨架曲线

图12所示为试验组合件骨架曲线和有限元分析组合件骨架曲线。从图12(a)可知：对于试件RCS-N1，RCS-N2，RCS-N3 和RCS-N6，由于形成梁铰受力机制，在峰值荷载之后，强度衰减较慢，没有出现突然的荷载下降，抗震性能优于发生构造破坏的RCS-N4和RCS-N5。当轴压比由0.40增加至0.45 时，构件的峰值荷载由RCS-N6 的96.22 KN 变为RCS-N1 的101.79 KN，但随着轴压比继续增大，RCS-N1，RCS-N2和RCS-N3的峰值荷载分别为101.79，102.29 和103.17KN，增幅较小，说明增大轴压比有助于构件的承载力的提高，但影响程度逐渐减弱；分析试件RCS-N1，RCS-N2，RCS-N3和RCS-N6可知，轴压比越高，试件承载力衰减越快。

由图12(b)可知：在弹性阶段，RCS-N7～RCS-N13 骨架曲线基本一致；在强化阶段开始出现较为明显的分化，当轴压比增大时，屈服点与峰值点的连线斜率下降，水平力增长变缓，RCS-N7峰值荷载为96.96 KN，而RCS-N13 峰值荷载为89.45KN。因此，在高轴压比下，随着轴压比增加，节点极限承载力略有降低；在峰值荷载过后，骨架曲线下降变快。

6.3 刚度退化

采用环线刚度K表示刚度退化特性，其表达式为

式中：Fi为i级位移角3 次循环对应的最大水平荷载；Δi为i级位移角3次循环最大荷载所对应位移。

按式(1)确定的RCS 组合件刚度退化曲线见图13，根据图13可知：

1)各个试件初始刚度在5.52～6.93，加载结束时，刚度下降至1.03～1.22，各试件刚度退化明显。

2)对于梁铰破坏的试件，在加载初期，轴压比大的构件具有较大初始刚度，但在组合件屈服之后，刚度退化曲线出现差异，表现为轴压比越大，刚度退化速率越快，但总体上，在试件屈服后，所有试件刚度退化均缓慢，说明在加载后期，蜂窝钢梁开始成为主要受力部件，导致试件表现出良好的抗震性能。

图12 RCS组合件骨架曲线Fig.12 Skeleton curve of RCS assemblies

3)对于梁铰破坏的试件(如RCS-N1，RCS-N2，RCS-N3 和RCS-N6)来说，在加载过程中组合件整体刚度都大于发生构造破坏的试件(RCS-N4 和RCS-N5)的刚度，且试件若发生构造破坏，其刚度退化速率大于梁铰破坏的试件。

图13 各试件刚度退化曲线Fig.13 Stiffness degradation curve of each specimen

6.4 延性

采用位移延性系数u定量分析轴压比对试件延性的影响。

式中：Δu为极限位移，取最大水平力下降到85%时对应的位移；Δy为屈服位移，各构件的屈服位移采用等能量法[13]确定，具体计算方法如图14所示，将试验与有限元计算结果整理见表6和表7。

由表6可知：对于梁铰破坏的试件，随着轴压比提高，试件RCS-N6 的延性由5.25 降低到RCS-N3 的4.11，延性降低21.7%，说明轴压比越高，构件的延性越低，而且根据文献[14-15]，其延性普遍在2～4 之间，而本试验组合件延性都不低于4，说明钢板箍可有效提高节点耗能性能，大幅度降低节点核心区混凝土的损伤，增加其延性。分析表6可发现，高轴压比可有效延缓组合件开裂；对于构造破坏来说，由于焊缝断裂，未能充分利用钢梁的塑性变形能力，试件过早进入极限状态，工程中应对焊缝质量提出较高要求，避免出现构造破坏。

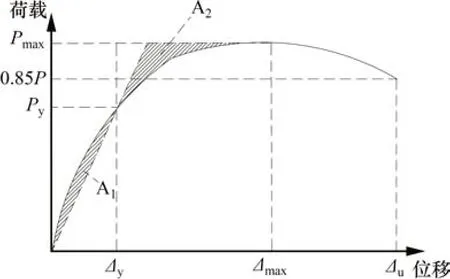
图14 能量等值法Fig.14 Energy equivalence method

对数值模拟结果分析可知，在高轴压比下，组合件的层间位移角仍可达到1/22 以上。一般来说，钢梁-混凝土柱组合件层间位移角为1/30～1/20[16-17]，说明此种组合件抗倾覆能力强，具有良好的抗震性能。在利用有限元分析中排除试验中各种干扰因素后可知，随着轴压比增大，组合件延性从RCS-N7 的3.24 变为RCS-N9 的2.64，延性降低，与试验结论一致。

6.5 耗能能力

采用等效黏滞系数he[18]定量分析在低周往复荷载作用下，轴压比对组合件耗能能力的影响，等效黏滞系数he计算简图如图15所示，表达式如下

式中：SEBF和SFDE之和表示某一加载级数下的滞回环面积，是组合件加载所需消耗的能量；SOBC和SODA表示某一加载级数下滞回环所对应的等效弹性结构，在正负方向加载所需消耗的能量。

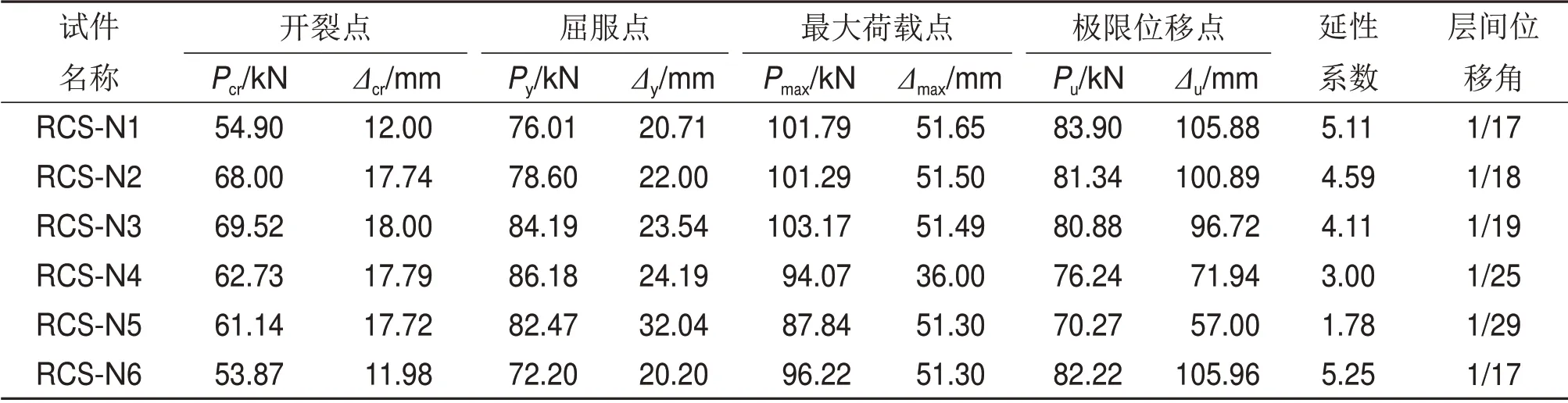
表6 试验RCS组合件骨架曲线特征点及延性系数Table 6 Characteristic points and ductility coefficient of skeleton curve of test RCS assemblies

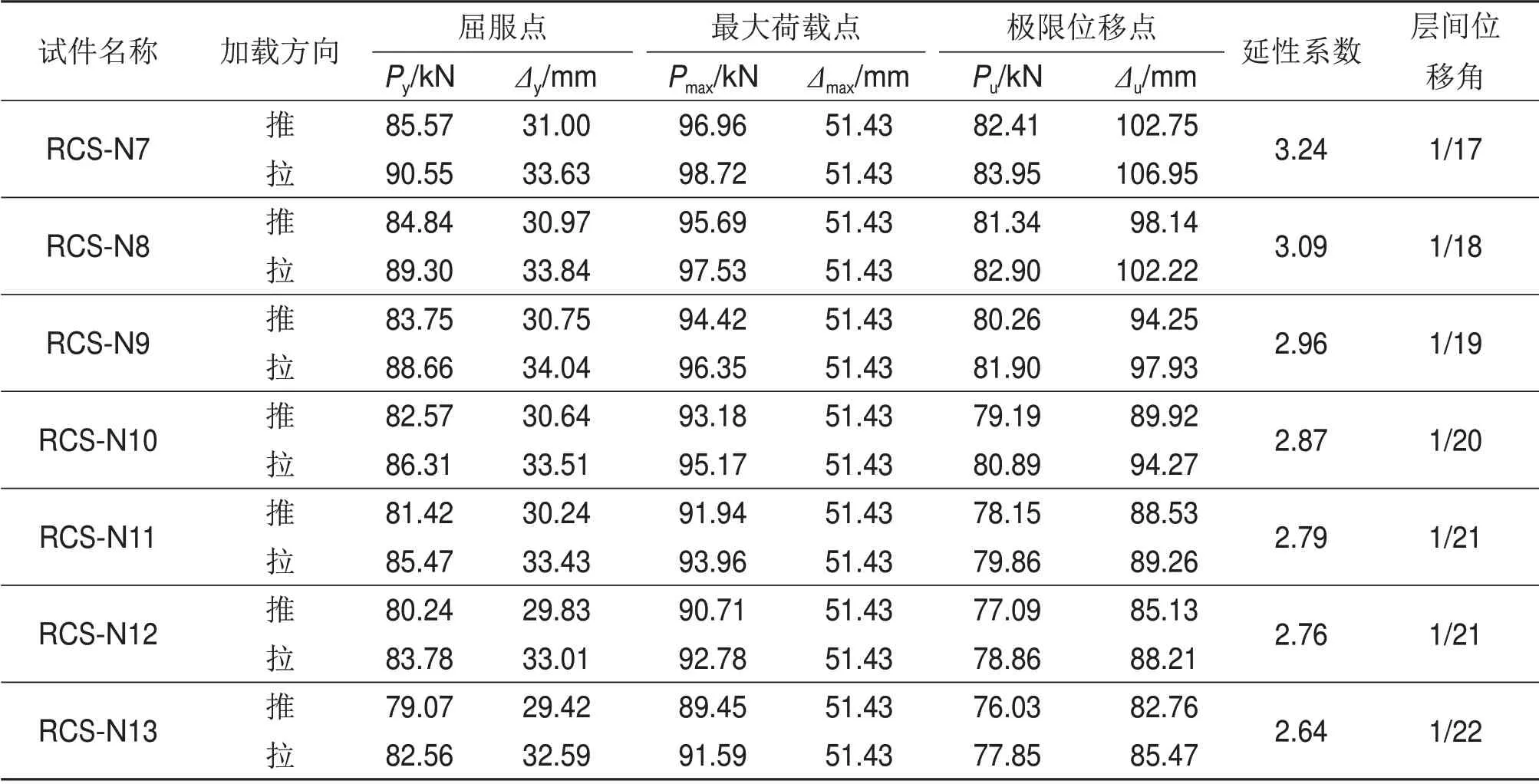
表7 有限元分析RCS组合件骨架曲线特征点计算结果Table.7 Finite element analysis of characteristic points of skeleton curve of RCS assemblies

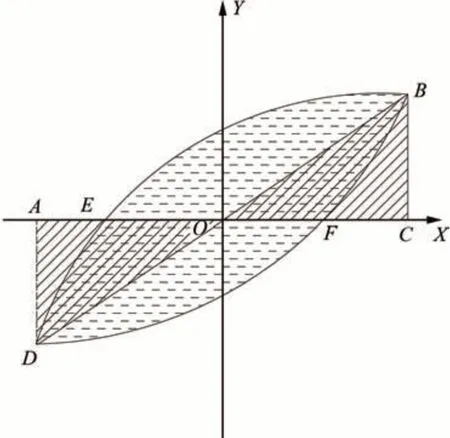
图15 等效黏滞阻尼系数的计算Fig.15 Calculative of equivalent viscous damping coefficient

选取各个试件屈服后的位移角(幅值)1/50(36.0 mm)，1/35(51.4 mm)，1/25(78.0 mm)和1/20(90.0 mm)下的滞回环面积计算相应的等效黏滞系数，构造破坏的组合件计算结果见表8，梁铰破坏的组合件及数值模拟结果如图16所示。

由图16(a)可知：对于梁铰破坏的组合件RCS-N1，RCS-N2，RCS-N3 和RCS-N6 来说，当轴压比从0.40 提高到0.65，组合件早期等效黏滞系数降低，但随着加载，轴压比大的组合件，等效黏滞系数增长较快，耗能能力有着显著增强，至加载结束，最大等效黏滞系数由0.474 提高到0.538，增大13.5%，这是因为在屈服早期，组合件耗能主要由柱端混凝土与钢梁共同承担，高轴压比下限制柱子裂缝开展，导致其塑性降低，引起弹性应变占比较大，但随着加载位移逐渐增大，梁铰机制的完全形成，钢材塑性应变占比变大，而高轴压比又引起节点区域连接紧密，减少节点区域各部件滑移，导致组合件耗能能力又显著增强。总的来说，轴压比升高，组合件早期耗能能力减弱，但随着加载，耗能能力增强。

表8 构造破坏试验RCS组合件等效黏滞系数heTable 8 Equivalent viscous coefficient he of structural failure test RCS assemblies

一般钢梁-RC 柱组合件最大等效黏滞系数为0.25～0.35[19-20]，本文组合件采用的节点形式在发生正常的梁铰破环时，最大等效黏滞系数可达到0.47，耗能能力增长34.3%以上，表明本文RCS梁柱组合件抗震性能优异。此类组合件若发生构造破坏，耗能能力则将发生大幅度下降，抗震性能变差。

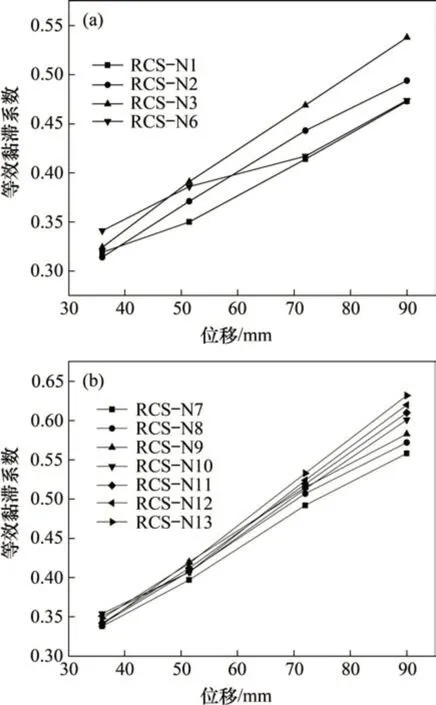
图16 RCS组合件等效黏滞系数Fig.16 Equivalent viscous coefficient of RCS assemblies

由图16(b)可知：高轴压比下，组合件刚达到屈服时，等效黏滞系数都在0.34 左右，但随着加载位移角增大，钢梁进入塑性发展阶段，组合件耗能能力快速增加，同时不同轴压比下各个组合件耗能能力出现明显差异，直至加载结束，RCS-N7和RCS-N13 最大等效黏滞系数分别为0.558 和0.632，可见随着轴压比增加，组合件耗能能力增强。

7 结论

1)以钢板箍约束节点核心混凝土的新型RCS组合件为基础，建立的有限元模型能够较好体现出其在循环往复荷载作用下的受力特点。

2)组合件的节点破坏形态符合“强柱弱梁、强节点弱构”的抗震设计原则，各项抗震指标表现良好，表明此种组合件节点形式有较好的受力性能。工程中应对节点处焊缝质量提出严格要求，避免出现构造破坏。

3)轴压比对此种梁柱节点抗震性能有着较为显著的影响。随着轴压比提高，构件滞回环变得丰满，延性降低，刚度退化速率加快，耗能能力有所提高。在一定范围内，较低轴压比有利于水平承载力的提高，但在高轴压比下，轴压比越大，水平承载力略有下降。