偏心环空中幂率流体层流流动特性数值模拟研究
Hicham Ferroudji, Ahmed Hadjadj, Titus N Ofei, Ahmed Haddad
(1. 布米尔达斯布加拉穆罕默德大学碳氢化合物与化学系, 石油装备可靠性与材料实验室, 布米尔达斯 35000;2. 马来西亚石油科技大学石油工程系,斯里依斯干达 32610;3. CRTI工业技术研究中心,阿尔及尔 16033)
1 Mathematical Model
1.1 Governing Equations
To study the impact of the inner pipe rotation and rheological parameters (yield stressτ0, consistency indexKand behavior indexn) on the axial and tangential velocity profiles of Herschel-Bulkley fluid in annular section, the flow is assumed to be fully developed,incompressible, steady and isothermal in laminar regime.
The continuity equation is expressed as:

where v is flow rate.
The momentum equation governing the flow in annulus is expressed in terms of τ in cylindrical coordinates (r,θ,z) for laminar regime as[10]:

wherevr,vθandvzare the velocity vector components (m/s), τrr, τθr, τzr, τθθ, τrθ, τzθ, τrz, τθzand τzzare the shear stress components(Pa),pis the pressure (Pa),ρis the density (kg/m3),gis the gravity(m/s2).
The rheological behavior of the non-Newtonian fluid is modeled as:

where τ is the shear stress(Pa),τ0is yield stress (Pa),Kis the flow consistency index (Pa·sn),nis the flow behavior index,is the shear rate (s–1).
1.2 Physical Description
In the present study, Herschel-Bulkley fluid flows through eccentric annulus (E=0.5) to simulate mud pattern during the drilling of horizontal well, in which the eccentricity is defined as:

whereEis eccentricity of the inner cylinder,eis the distance between the centers of the inner and outer pipes(m),Dois diameter of the outer cylinder(m),Diis diameter of the inner cylinder(m).
To predict the flow regime of yield power-law fluid in the annulus, Reynolds number is calculated using the relationship presented by K. Madlener et al[11]:
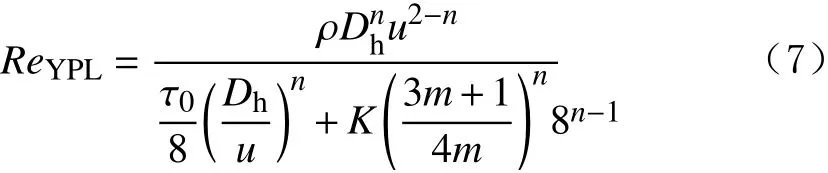
whereReYPLis the Reynolds number of yield power-law fluid,uis the bulk flow velocity(m/s),mis the local shear rate(s–1),Dhis the hydraulic diameter(m) which are calculated as:
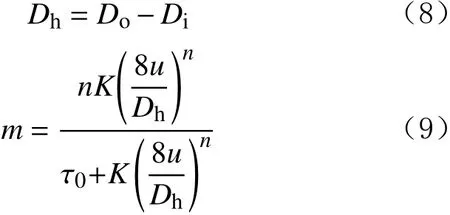
To prevent the entrance effects, the length of the cylinders is selected to be longer than hydrodynamic entry length, which is given as[12]:

whereLh,laminaris length of the hydrodynamic entry.
The rheological parameters of Herschel-Bulkley fluid and geometry characteristics are:K=16 Pa·sn,n=0.43, τ0=32 Pa,Do=65 mm,Di=40 mm.
1.3 Simulation Method
The domain of the fluid flow is meshed into 800 000 elements (20 radial divisions, 80 circumferential divisions and 500 axial divisions), where the number of elements is selected to ensure the results independence of mesh model used as well as keeping the number of elements as low as possible to save computational time,as shown in the Fig. 1 and Fig. 2. The commercial code ANSYS Fluent 17.0 based on finite volume method is used to solve the differential equations, where the flow equations are integrated over each control volume. The solution is assumed to be converged, when the convergence criteria 10–4is reached.

Fig.1 Computational grid and domain flow of the eccentric annulus

Fig.2 Mesh independence study
2 Results
2.1 Model Validation
Results obtained from the numerical model are compared to those of experimental work of C. Nouar et al[3]are shown in Fig. 3. The Simulation and experimental results are in good agreement in which the mean error are of 7.7% and 6.4% for dimensionless axial and tangential velocity, respectively.

Fig.3 Comparison of numerical and experimental velocity profiles
Comparison of the experimental and numerical results reveals the ability of numerical simulation to provide accurate results.
2.2 Axial Velocity
Fig. 4 exhibits that the increase of the inner pipe rotation from 100 to 400 r/min causes an increase of 120 %of the maximum axial velocity in the narrow region of the annulus, which could improve the well cleaning process by the transportation of cuttings from the lower side of the horizontal annulus preventing the formation of cuttings bed. However, the increase of the inner pipe rotation,induces a reduction of the velocity gradient (∂u/∂r) near the outer pipe in the wide region of the annulus. Similar to the conclusion reported by C. Nouar et al[3].

Fig.4 Axial and tangential velocity profiles for various inner pipe rotations (τ0=32 Pa, K=16 Pa·s n, n=0.32)
Fig. 5 shows that the increase of yield stress from 8 to 32 Pa causes a decrease of 6.1 % and 3.6 % of the maximum axial velocity in the wide and narrow regions,respectively.

Fig.5 Axial and tangential velocity profiles for various yield stresses (ω = 131.84 r/min, K=16 Pa·s n, n=0.43)
When the consistency index diminishes from 16 to 4 Pa·sn, the axial velocity profile becomes more flat in the wide region of the annulus, however, a negligible effect is observed for the narrow region, as exhibited in the Fig. 6.

Fig.6 Axial and tangential velocity profiles for various consistency indexes (ω = 131.84 r/min, τ0=32 Pa, n=0.43)
As the behavior indexndecreases from 0.8 to 0.2,the axial velocity profile becomes flat in the wide region of the eccentric annulus, as shown in the Fig. 7. While a negligible effect is observed in the narrow region except forn=0.8, where the negative values of the axial velocity profile could be attributed the rotation of the inner pipe which probably increase pressure drop in the annulus.
2.3 Tangential Velocity

Fig.7 Axial and tangential velocity profiles for various behavior indexes (ω = 131.84 r/min, τ0=32 Pa, K=16 Pa·s n)
For all range of the inner pipe rotation, the tangential velocity decreases dramatically near the inner pipe rotation in the wide region of the annulus. As the fluid moved away from the inner pipe, this decrease becomes gradual except forω=100 r/min, the decrease becomes more gradual in the center of annulus. After that, the tangential velocity begins to decease sharply again until the outer pipe, as presented in the Fig. 4.
As the yield stress diminishes, the tangential velocity decreases more gradually in the center of annulus in the wide region, while a similar variation is observed near the outer and inner pipes, as showed in the Fig. 5.
It can be seen from Fig. 7 that tangential velocity profile in the center of annulus of the wide region decreases more gradually as the behavior index decreases from 0.8 to 0.2 where the tangential velocity profile presents negative values from center of the annulus until the outer pipe. The negative values of the tangential velocity explained by the presence of a secondary flow(also called counter rotating swirl) which rotates in the opposite direction of the inner pipe. The appearance of the secondary flow could decrease carrying capacity of the drilling mud, which affects the whole cleaning process.
In the narrow region of the annulus, the tangential velocity profile decreases dramatically as the fluid moves away from the inner pipe. Fig. 4 to Fig. 7 show that the variation of the inner pipe rotation and rheological parameters have a slight effect on the tangential velocity.
2.4 Pressure Drop Gradient
As can be seen in Fig. 8, the increase of the inner pipe rotation from 0 r/min to 400 r/min causes a decrease of pressure drop gradient of yield power-law fluid, this decrease is estimated around 10% for all eccentric annulus (E=0.2, 0.4, 0.6 and 0.8). Since shear thinning phenomenon tends to reduce the pressure drop of yield power-law fluid, inertial effects induced by rotation of the inner pipe are dominated by shear thinning phenomenon in the annulus. This trend is also depicted by R. M. Ahmed et al[7].

Fig. 8 Effect of the pipe rotation on pressure drop gradient for different eccentricities (Re = 12.05, τ0 = 32 Pa,K = 16 Pa·s n, n = 0.43)
Fig. 9 depicts the effect of the yield stress of yield power-law fluid on pressure drop gradient, as shown in the figure, the increase of the yield stress from 8 Pa to 32 Pa induces an increment of 15% of pressure drop gradient for all eccentricities. This increase could be attributed to additional required stress on the fluid to initiate the flow which enhance inertial effects of yield power-law fluid in the annulus.

Fig.9 Effect of the yield stress on pressure drop gradient for different eccentricities (Re = 12.05~14.10, ω =200 r/min, K = 16 Pa·s n, n = 0.43).
Fig.10 displays variation of pressure drop gradient of yield power-law fluid in the annulus when the flow consistency index increases from 4 Pa·snto 16 Pa·sn. As seen in the figure, an increase of 150% of pressure drop gradient for all eccentricities caused by the increment of the flow consistency index. This considerable increase could be explained by the increase of the flow resistance in the annulus due to the increasing fluid viscosity.
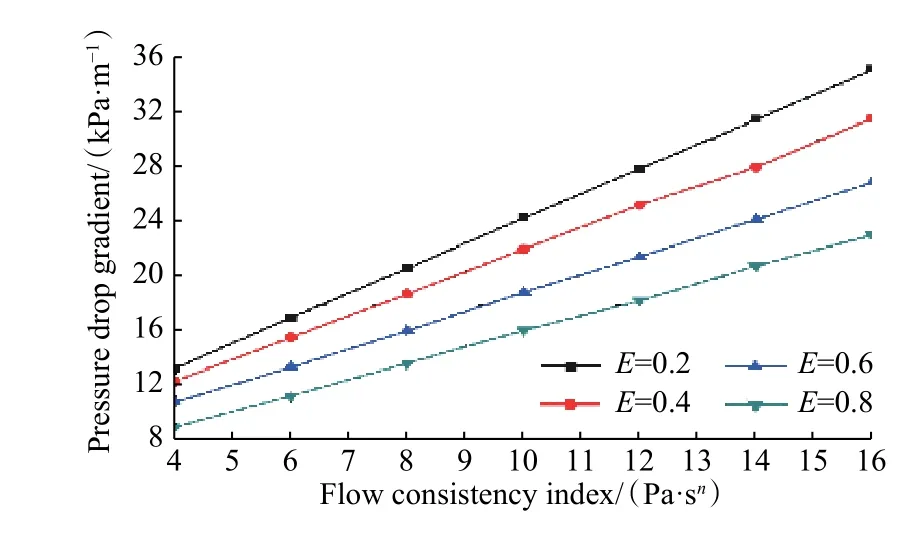
Fig.10 Effect of the flow consistency index on pressure drop gradient for different eccentricities (Re =12.05~30.66, ω = 200 r/min, τ0 = 32 Pa, n = 0.43).
Moreover, it can be stated that as the flow consistency index increases, the effect of the eccentricity of cylinders on pressure drop gradient becomes more pronounced.
Fig. 11 exhibits impact of the flow behavior index on pressure drop gradient of yield power-law fluid. As can be seen, an exponential increase of pressure drop gradient as the flow behavior index gets closer from Newtonian behavior where the fluid is less affected by shear thinning phenomenon, which makes inertial effects dominate the flow of yield power-law fluid in the annulus. It was also observed that for low values of the flow behavior index, the eccentricity of cylinders has a slight effect, however, as the flow behavior index gets greater, pressure drop gradient of yield power-law fluid decreases with the increase of the eccentricity.

Fig.11 Effect of the flow behavior index on pressure drop gradient for different eccentricities (Re = 1.48~37.54, ω = 200 r/min, τ0 = 32 Pa, K = 16 Pa·s n).
For all rheological parameters and inner pipe rotation, pressure drop gradient of yield power-law fluid decreases with the increase of the eccentricity.
3 Conclusions
1) The increase of the inner pipe rotation from 100 to 400 r/min increases the axial velocity in the narrow region of the eccentric annulus, which could enhance the cleaning process in the lower part of the eccentric annulus.However, a slight effect is observed for the maximum axial velocity in the wide region of the annulus.
2) For the behavior indexn=0.8, the fluid near the inner pipe in the narrow region of the annulus tends to flow in the opposite direction of the main flow, which increases the pressure drop in the annulus and diminishes the carrying capacity of the mud.
3) Low value of the behavior index (n=0.2) causes appearance of the secondary flow in the wide region of the annulus, which rotates in the opposite direction of inner pipe rotation, this could affect the whole cleaning process.
4) The variation of the inner pipe rotation and rheological parameters of the Herschel-Bulkley fluid have a negligible effect on the tangential velocity profile in the wide region for an annulus ofE=0.5.
5) The increase of the inner pipe rotation from 0 rpm to 400 rpm causes a decrease of 10% of pressure drop gradient of yield power-law fluid for all eccentric annulus(E=0.2, 0.4, 0.6 and 0.8).
6) As the flow behavior index gets closer from the Newtonian behavior, the eccentricity of cylinders pressure drop gradient of yield power-law fluid decreases with the increase of the eccentricity.
———动力工程系

