33 t轴重内燃机车方案及机车曲线黏着问题研究
曲天威, 罗世辉, 马卫华
(1. 西南交通大学 牵引动力国家重点实验室, 四川 成都 610031;2. 中车大连机车车辆有限公司, 辽宁 大连 116022)
2014年底我国第一条30 t轴重重载铁路(瓦日铁路,即原晋中南通道)建成通车,与之相适应的30 t轴重重载运输技术体系基本形成[1],该体系中的牵引机车轴重在27~33 t范围,均为电力牵引,若重载铁路电网因战争、极端自然灾害等不可控因素无法提供外部能源,则将对运输产生严重影响,因此开展30+3t轴重(通过配重实现30 t轴重和33 t轴重间的转换,以下简称“33 t轴重”)内燃机车技术方案研究及相应的动力学分析,对完善我国30 t轴重重载技术体系和内燃机车型谱具有重要意义。
我国30 t轴重电力机车HXD1F和HXD2F单节车均为Bo-Bo轴式,内燃机车因柴油机、主发电机、燃油箱等的集中质量大,单节车均为Co-Co轴式[2]。Co转向架轴距大,曲线黏降现象对机车牵引性能发挥影响显著,采用径向转向架是机车实现高黏着利用的重要措施且取得了极大成功[3],国内外对其机理的研究较多[4-6],我国在少量直流机车上也有应用[7-8]。
交流传动技术使机车功率显著提升,黏着成为机车充分发挥牵引能力的重要因素。国内外试验和理论研究[9-12]均表明,黏着达到饱和后黏着力总体随蠕滑率进一步增大呈下降趋势,且机车运行速度越高这一趋势越明显。过去的机车动力学研究和机车黏着研究都很少关注同一轮对左右侧车轮的黏着系数差异,也缺乏对曲线黏着的定量分析,本文基于提出的33 t轴重内燃机车方案,建立了发挥牵引力状态下的机车动力学模型并对此开展研究。
1 33 t轴重内燃机车总体技术方案
中车大连公司25 t轴重大功率交流传动内燃机车技术平台,是以HXN3型干线重载内燃机车研发为基础而搭建的,该型机车额定功率4 400 kW,最大起动牵引力620 kN,恒功率速度范围23~120 km/h,满足干线牵引5 000~6 000 t的要求[13]。
本文基于该技术平台,借鉴平台典型车型HXN3、HXN3B的特点,吸收国外大轴重内燃机车成功经验[3],确定33 t轴重内燃机车的初步方案。
1.1 机车总体布局与主要技术参数
33 t轴重重载内燃机车动力系统与HXN3相同,均采用电子喷射装置的16V265H型柴油机,高可靠性的架控交流传动系统,微机网络控制系统,高集成化的主辅发电机,以及计算机控制的空气制动系统等。车体采用独立的弹性隔振司机室、内走廊、整体承载、燃油箱与底架一体化的结构方式。
轴重增加部分主要由3部分组成,分别是转向架结构增强需要的质量,车体结构增强需要的质量,以及车体配重。车体配重用于实现机车30 t轴重与33 t轴重之间的转换。机车总体布局见图1,主要技术参数见表1。
新方案与HXN3机车除了轴重不同,还有以下不同之处:①牵引、制动特性的恒功率速度点更低;②转向架质量和悬挂参数不同,且为实现高黏着利用,提出了三轴传统转向架和三轴径向转向架2种方案进行比较;③关键承载部件强度设计要求不同。

图1 机车总体布局方案

表1 33 t轴重内燃机车主要技术参数
1.2 机车牵引与制动特性
相比25 t轴重机车,33 t轴重机车的黏着质量增大了32%,机车的起动牵引力和持续牵引力相应增加,在电机特性不变前提下,为匹配起动牵引力增大需降低恒功率速度点。据此构筑8档位牵引特性曲线(见图2)及制动特性曲线(见图3),机车持续制轮周牵引功率和电制动功率为3 700 kW。
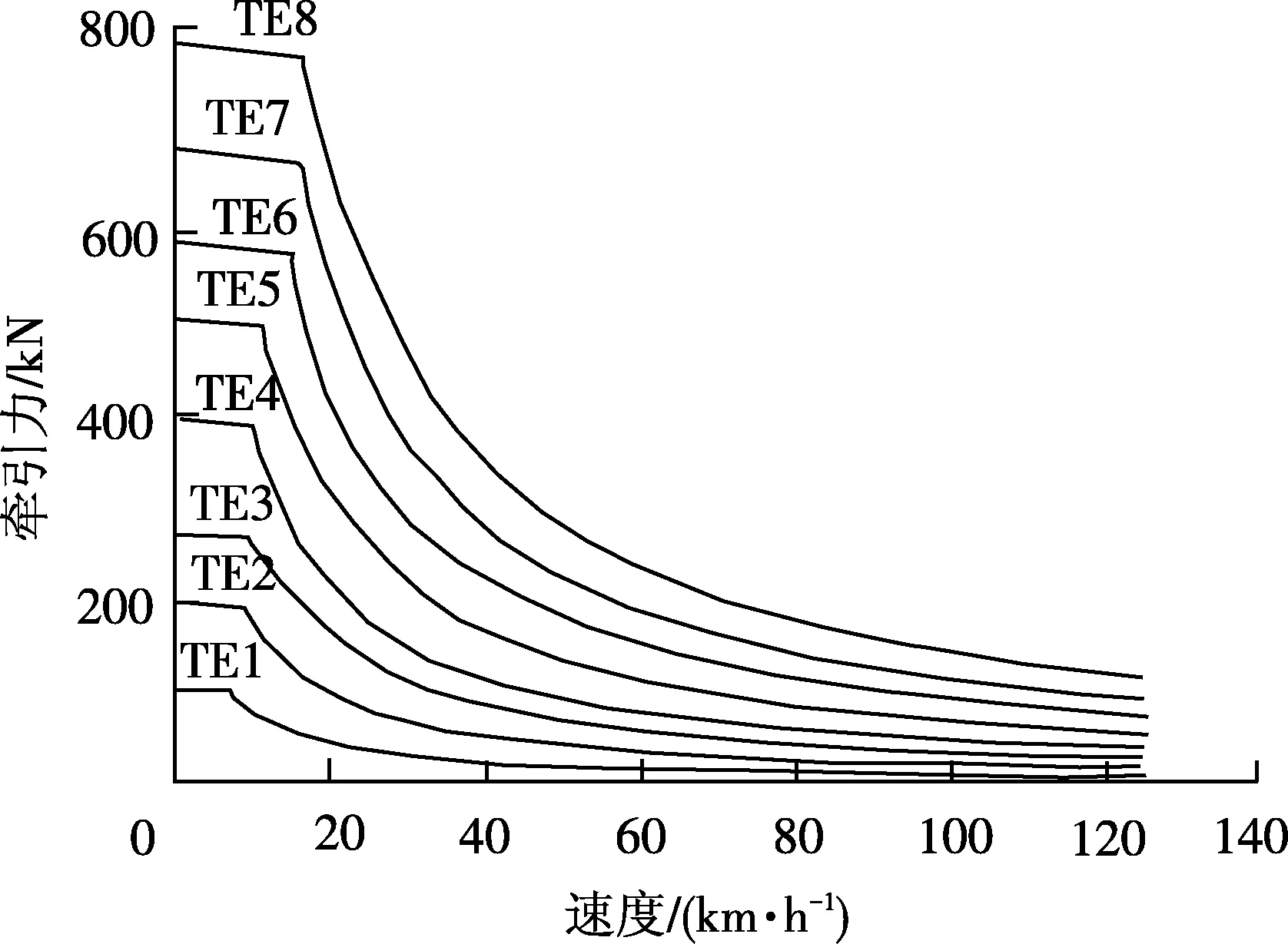
图2 牵引特性曲线

图3 制动特性曲线
2 重载转向架方案
大功率重载内燃机车均采用三轴转向架,三轴转向架又可分为传统转向架和径向转向架2种。其中径向转向架在美国EMD公司大轴重内燃机车上应用非常成功,对改善机车曲线通过性能、减小轮缘磨耗和减小曲线黏降效果显著。33 t轴重内燃机车总体方案中,这2种转向架方案均可作为选择。
2.1 三轴传统转向架方案
借鉴25 t轴重大功率内燃机车三轴传统转向架技术平台,可确定33 t轴重机车三轴转向架基本方案,见图4。

图4 三轴传统转向架基本方案
33 t轴重内燃机车采用的转向架总质量设为31.5 t,与25 t轴重HXN3型、HXN3B型内燃机车转向架总质量22.9、25 t相比分别提高了37.6%和26%,质量增加部分用于全面加强转向架的各承载结构。
在悬挂设计方面,依据120 km/h速度级货运机车特点,一、二系总静挠度约为125 mm,HXN3、HXN3B机车二系橡胶旁承静挠度超过15 mm,在运用中横向复位力较弱,此处取10 mm作为二系静挠度,取115 mm作为一系静挠度,总静挠度125 mm,再依据机车质量分配可确定转向架一、二系悬挂的垂向刚度,并通过单机惰行下的动力学参数优化,得到机车的最优动力学参数。
2.2 三轴径向转向架方案
径向转向架的原理是两端轮对能够产生一定的相互回转,使得各轮对都尽可能地靠近曲线半径方向。在图4传统转向架中增加图5所示径向调整机构,并进行适应性改动,可得到径向转向架方案,其动力学参数除端轴一系悬挂参数外,均保持不变。端轮对与导向机构(可相对构架绕铅垂轴转动的)导向梁通过轴箱拉杆相连,端轮对左右轴箱相对构架具有纵向运动自由度,因此端轮对轴箱的一系悬挂设计是径向转向架的关键,具体方案见图6。图中附加橡胶叠层弹簧在轮对相对构架发生横向和摇头运动时将发挥作用,提供足够的横向刚度和适当的摇头刚度,但不影响其径向调整,也是径向转向架端轴一系悬挂设计的关键。

图5 三轴径向转向架的径向调整机构

图6 径向转向架端轮对一系悬挂方案
2.3 33 t轴重机车的轮轨廓形
我国30 t轴重重载技术体系中钢轨采用75 N廓形[14],机车车轮采用JM3廓形,采用谐波法计算轮轨匹配等效锥度结果见图7,在7 mm以内横移振幅范围的接触等效锥度约为0.094。

图7 JM3/75N轮轨匹配等效锥度
3 牵引状态下的机车动力学建模
机车车辆是典型的多体系统,Kortüm[15]对车辆多体系统采用牛顿-欧拉法建立动力学普遍方程的过程进行了详细介绍。在多体动力学中采用通路矩阵或关联矩阵来表达系统的运动、力元等的拓扑构型,采用体矢量描述刚体上的质心,铰和力元连接点等特征点的位置、速度和加速度[16]。现今成熟的多体系统程序为机车车辆动力学分析提供了高效手段,本文采用Simpack程序进行建模和仿真。
3.1 牵引力的建模
根据第2节中的机车结构特点、动力学参数和轮轨廓形,可建立常规的单机动力学模型,见图8。其中电机及齿轮箱视为一个刚体,仅具有相对车轴的转动自由度,该刚体非车轴端通过吊杆悬吊于构架,模拟机车的轴悬式驱动装置。

图8 机车动力学模型(后转向架视图)
在此基础上,对每个轮对建立力元(Simpack中93号力元),由驱动装置向轮对施加扭矩。为避免瞬时冲击过大,扭矩值在一定时长内由零线性增至最大值并保持,最大值为牵引特性曲线(图2)中对应速度的牵引力和车轮半径的乘积,取正值。
3.2 牵引力的平衡
由于对每个轮对均施加有驱动扭矩,若不加以平衡,则机车将处于加速过程。为计算某速度下的曲线黏着系数,必须在加有牵引扭矩的模型中再增加车钩阻力,且车钩阻力始终与牵引力平衡。通过将具有长度的车钩一端与机车铰接,另一端与一个刚体(虚拟列车)铰接,且该刚体即虚拟列车的运动关系定义为沿轨道恒速前进(Simpack中9号铰,并取零自由度),实现任意线路上的牵引力平衡。
3.3 模型检验——轴重转移计算
机车采用传统转向架或径向转向架动力学模型的区别仅在于转向架端轴的水平定位不同,垂向特性一致,轴重转移计算可不做区别,但径向转向架可显著减小曲线通过时的冲角,因此曲线黏降与传统转向架存在显著差别。可以通过机车起动时的轴重转移计算检验模型的准确性。
轴重转移与牵引黏着系数有关,黏着系数越大轴重转移越大。取轮轨黏着系数为0.41[17],33 t轴重机车的单轴牵引力为133 kN,每个轮对的驱动扭矩约69 kN·m,起动计算速度取1 km/h,可得到各轮对轴重变化,其中机车前转向架一位轮对减载量最大,以此作为机车轴重转移衡量指标,见图9。结果显示对应0.41黏着系数的轴重转移为11.3%。

图9 最大起动牵引力下的轴重转移
美国GM公司径向转向架内燃机车通过试验得到0.35黏着系数时轴重转移约为10%,0.25黏着系数时轴重转移仅为7%[3],由图9可查出对应这2个黏着系数的轴重转移分别为9.7%和6.7%。差异的形成与牵引点高度、车钩高度、一系和二系悬挂刚度、轴距等诸多因素有关,但这两种同轴重等级的交流传动重载货运内燃机车的轴重转移指标具有可比性,可间接验证所建模型的合理性和准确性。建议应用本方法时,黏着系数取值大于实际允许值(如取0.45),以避免黏着不够引起的轮对空转。
4 曲线黏降现象及曲线黏着定性分析
4.1 导向轮对两侧车轮的横向蠕滑率
以曲线外轨侧(以下称为左侧)为例,轮轨接触斑的空间几何关系见图10。曲线上左右车轮的前进速度vl,r=v(1±b0/R),其中下标l, r表示左右侧轮,v为名义前进速度,b0为左右轮滚动圆间距之半,R为曲线半径,r为车轮滚动圆半径,ω为轮对转速,轮对连体坐标与参考坐标的名义几何夹角为β=l0/R,l0为端轴距之半,轮轨接触的相关角度见图10(a)。

图10 左侧车轮接触斑空间位置与速度
根据图10(b)的几何关系及纵向蠕滑率γ1和横向蠕滑率γ2定义,可得到导向轮对左右侧车轮横向蠕滑率(相对接触斑车轮坐标系)
( 1 )

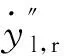
( 2 )
式中:Ω=v/R为轮对连体坐标系在投影面的旋转角速度,矢量方向沿Z″正方向;δxl,r为左右轮接触斑相对轮对中心的纵向偏离量,矢量方向分别沿X″正、负方向,偏离量由超前(落后)角确定
δxl,r=rl,rsinζl,r
( 3 )
将式( 3 )代入式( 2 ),得到
( 4 )
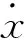
( 5 )
进一步考虑到在曲线上转向架后端轮对近似占据径向位置,转向架摇头角约为-β,对前轮对而言ψ≈-β,因此曲线上前轮对的冲角约为α≈-2β。有
( 6 )
式(6)表明到达曲线稳态位置时,轮对两侧车轮的横向蠕滑率由两部分组成:一部分与轴距和名义曲率成正比;另一部分与滚动圆半径、钢轨曲率、接触斑超前(落后)角和车轮接触角有关。式( 6 )证明曲线通过时内侧轮冲角αr始终超过外侧轮冲角αl,两者之差为

( 7 )
式( 6 )中车轮滚动圆半径显著小于端轴距,且超前(落后)角是一个较小量,说明曲线通过时由几何冲角引起的导向轮对左右轮的横向蠕滑率占主导,但两者因接触斑位置不同有较小差异。
4.2 曲线黏降
机车可用牵引黏着与纵向蠕滑率有关,但纵向和横向蠕滑率之间又相互影响。Frederich[18]忽略自旋蠕滑给出了下列拟合公式描述了纵、横向蠕滑系数fx、fy与纵、横向蠕滑率的关系
( 8 )
依据式( 8 )可得到图11,直观地体现横向、纵向蠕滑率对纵向、横向蠕滑系数的影响。

图11 蠕滑系数与蠕滑率的关系[18]
图11显示横向蠕滑率越大则纵向蠕滑特性曲线越低,意味着同样纵向蠕滑率下对应可得到的纵向牵引力越小,由于曲线上始终存在冲角引起的横向蠕滑率,因此曲线上的牵引黏着降低,这一现象称为曲线黏降。
4.3 曲线黏着定性分析
原理上摩擦发生在一个方向,只有一个总的蠕滑特性曲线,蠕滑力在横向、纵向的分量只是其坐标决定的。设总蠕滑率为ξ,总的摩擦力T=f(ξ)由蠕滑特性确定并与总蠕滑率ξ方向相反,其沿轮轨接触斑车轮坐标的分量为Tx、Ty,即纵、横向黏着力。总蠕滑率为纵、横向蠕滑率的合成
( 9 )
合成黏着力的2个分量满足
(10)
根据黏着系数的定义,由式( 9 )、式(10)并考虑式( 6 ),且仅考虑几何冲角效应,可得到适用于所有半径曲线的黏着公式
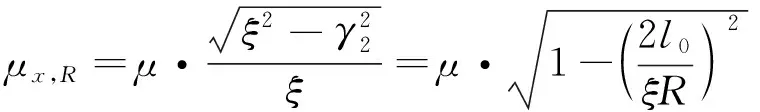
(11)
式中:μx,R为曲线可用黏着;μ为摩擦系数(即平直道纯纵向蠕滑下的可用黏着)。
以本文机车通过R300曲线为例,2l0=3 680 mm,得到μx,R=79%μ(取ξ=2%)、87%μ(取ξ=2.5%)或91%μ(取ξ=3%)。不同的总蠕滑率得到的结果不同。总蠕滑率的合理取值与实际的运行速度和轮轨蠕滑特性有关。
针对交直传动内燃机车,中国铁道科学研究院在0~30 km/h速度范围,试验得到了机车小半径曲线上的黏着系数与直线黏着系数的关系[19]
μx,R=μ·(0.805+0.000 355R)
(12)
依据式(12)得到R300曲线上μx,R=91%μ,与式(11)总蠕滑率取ξ=3%的结果相同。交直传动内燃机车的起动黏着系数仅取0.32,远低于高黏着机车0.41的黏着系数,不宜将式(12)用于高黏着机车。大量试验显示,在考虑另一方向蠕滑率时,纵、横向蠕滑率在达到1.5%~2%时均已越过特性曲线的零斜率点[20],两者同时达到1.5%~2%时的总蠕滑率为2.1%~2.8%,因此利用式(11)进行曲线黏着计算时,偏于保守,建议总蠕滑率ξ取2%~2.5%。
5 33 t轴重内燃机车曲线黏着计算
5.1 计算工况
依据图7,可将R300曲线视为典型的“小半径曲线”,其不考虑轮缘效应的纯滚线偏离线路中心线已超过轮轨间隙;将R1 000曲线视为典型的“大半径曲线”,其纯滚线偏离线路中心线略超过3 mm的轮轨关系线性化的横移振幅。在这2种曲线条件下,对机车采用2种不同转向架方案的曲线黏着进行对比。
大、小半径曲线均依次由直线段、进缓和曲线段、圆曲线段组成。曲线超高均为120 mm,对应大、小半径曲线的超高顺坡分别为1‰和2‰。
曲线起动计算时,机车速度取1 m/s低速,起动扭矩取最大扭矩(轴重转移计算中采用的每轴69 kN·m)的90%,扭矩在机车完全进入圆曲线时由零线性增至规定值。曲线通过计算时,未平衡离心加速度取0.6 m/s2,其对应R300曲线通过速度73 km/h,对应R1 000曲线通过速度134 km/h(该速度超过机车最大运用速度,仅为研究性计算取值)。参考图2中满功率手柄位(TE8),对应这2个速度的牵引力分别为200、100 kN(此值为推算值仅用作理论分析),对应向车轴施加的扭矩分别为17.5、8.75 kN·m。通过R300曲线的计算时长取30 s,通过R1 000曲线的计算时长取20 s,扭矩在0~5 s内由零线性增至规定值。根据文献[17]的牵引黏着系数推荐公式,起动计算时摩擦系数取0.41,曲线通过计算时摩擦系数均取0.31。用FASTSIM得到2种条件下的纵向最大可用黏着特性曲线,见图12。
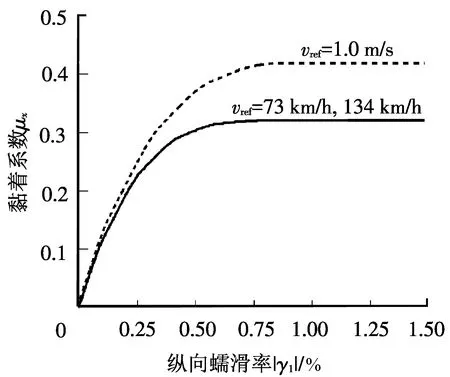
图12 2种条件下的纵向最大可用黏着特性
5.2 曲线起动过程中的曲线黏着
为判定轮轴是否能可靠发挥牵引力,本文以图12所示的特定黏着特性为前提,且该特性始终保持不变,以纵向蠕滑率1.25%(绝对值,实际方向与牵引力相反。下文中均指绝对值)作为机车仍能可靠发挥牵引力的极限值,轮对左右侧车轮纵向蠕滑率均超过此值时,即认为轮对失去黏着。该值仅因本文计算需要而设定,不是工程推荐值。
5.2.1 小半径曲线
在施加扭矩的过程中,同一时刻左侧轮纵向蠕滑率大于右侧,随扭矩增大,两者差异缩小,在小半径曲线上几乎在同时刻达到1.25%的纵向蠕滑率,见图13(a),在大半径曲线上左侧车轮先于右侧车轮达到1.25%,见图13(b)。只要一侧车轮保持黏着,整个轮对就不会失去黏着。

图13 车轮纵向蠕滑率时间历程
采用传统转向架时,机车最前端一位轮对左右侧车轮的纵向黏着系数-蠕滑率的结果见图14(a),两者在同一时刻达到1.25%的纵向蠕滑率限值,扭矩加载过程的左右轮牵引力见图14(b),扭矩从第80 s开始由零增长至90%×69 kN·m(消除10%轴重转移影响),达到极限时左右车轮的牵引力见图14(b)中标出的数值。右侧轮输出牵引力显著超过左侧轮,去除轴重转移因素(0.303黏着系数下对应轴重转移比0.41黏着下多计入了3%),曲线可用黏着为直线上的77%(0.303/0.41+3%),与第4.3节定性分析中总蠕滑率取ξ=2%所得79%的结果相近,由于式(11)中未计入式( 6 )中等式右边第2项次要因素的影响,因此得到的结果略大于数值仿真结果。

图14 机车一位轮对牵引力发挥(传统转向架)
保持同等计算条件,得到采用径向转向架的类似结果见图15,导向轮对左右两侧车轮在同一时刻达到1.25%的纵向蠕滑率限值,达到限值时左右车轮的牵引力见图15(b)中标出的数值。去除轴重转移因素,曲线可用黏着为直线上的87.1%(0.35/0.41+1.7%)。
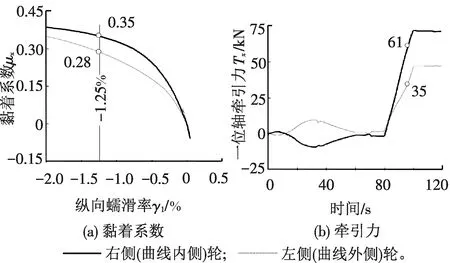
图15 机车一位轮对牵引力发挥(径向转向架)
5.2.2 大半径曲线
R1 000大半径曲线上起动计算结果见图16、图17,在达到大牵引力时2种转向架的结果基本相同。左侧车轮先于右侧车轮达到1.25%,并随扭矩增大继续增大,直至右侧车轮的纵向蠕滑率也达到1.25%时为止,此时左侧车轮纵向蠕滑率略超1.5%,对应左右车轮的牵引力见图16(b)和图17(b)中标出的数值。去除轴重转移因素,2种转向架曲线可用黏着为直线上的95.7%(0.39/0.41+0.6%),按式(11)得到的值为98.3%(取ξ=2%),略大于数值仿真结果。

图16 机车一位轮对牵引力发挥(传统转向架)

图17 机车一位轮对牵引力发挥(径向转向架)
在曲线起动过程中,由于径向调整机构的作用,2种转向架一位轮对左右侧车轮牵引力的时间历程表现出很大的差异。径向转向架在极低速度下通过曲线时,惰行或小牵引力下即能发挥有利作用,大牵引力时两者差别缩小,径向转向架对提高小半径曲线的起动黏着具有显著优势。
5.3 曲线通过过程的曲线黏着
5.3.1 较大欠超高通过
机车以0.6 m/s2未平衡离心加速度欠超高通过曲线且发挥相应牵引力时,一位轮对纵向蠕滑率时间历程见图18。图中大小半径曲线上纵向蠕滑率绝对值远低于1.25%极限值,机车工作在牵引黏着特性曲线的上升段(见图12),可正常发挥牵引力。图18还显示,径向转向架相比传统转向架在2种曲线上均有优势,体现在同样牵引能力下车轮的滑动量明显更小。

图18 欠超高通过曲线时的纵向蠕滑率
5.3.2 较低速度通过
当机车通过曲线的速度低于上述计算工况时,其输出牵引力将按恒功率曲线增大。由于摩擦系数在机车起动后随速度增加初期下降很快,达到0.32后再随速度降低的程度很缓慢,以0.32为可用黏着,计算机车以30~60 km/h速度通过2种曲线时一位轮对的纵向蠕滑率,结果见图19。图19(a)表明传统转向架在36 km/h以上的速度通过小半径曲线时可发挥100%牵引力,而径向转向架的相应速度可低至32 km/h;图19(b)表明,机车以30 km/h以上速度通过大半径曲线时,2种转向架均可发挥100%牵引力,径向转向架的车轮滑动量显著小于传统转向架。

图19 较低速度通过时的纵向蠕滑率
图19中还可看到,在35 km/h速度以下,牵引力随速度呈反比增大很快,且蠕滑率绝对量增长非常快,因此速度越低黏降影响越显著。
大半径曲线上转向架依靠蠕滑导向,左侧车轮纵向蠕滑率在牵引基础上增加导向部分,右侧车轮纵向蠕滑率在牵引基础上减去导向部分,因此左侧轮的纵向蠕滑率显著超过右侧车;随着曲线半径减小,不仅参与的横向蠕滑率增大,导向力矩也逐渐减小直至成为导向阻力矩,左右轮纵向蠕滑率差异减小,最终演变成图18(a)和图19(a)。
5.3.3 低速度通过
机车保持25 km/h速度通过曲线,通过降低驱动扭矩,观察机车一位轮对纵向蠕滑率,至少一侧轮的绝对值不应超过1.25%,得到对应的曲线黏着。
从图19可知,在小半径曲线、大牵引力下左侧轮滑动量略小于右侧轮,在大半径曲线、大牵引力下右侧轮滑动量小于左侧轮。此处计算中,考察滑动量更小的车轮,即小曲线用左侧轮,大曲线用右侧轮判别,结果见图20。
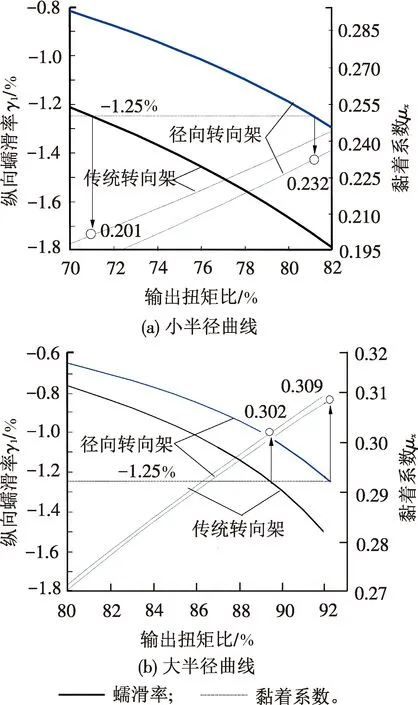
图20 低速通过曲线的蠕滑率与黏着系数
能达到的扭矩比即代表曲线上可用黏着相对于直线黏着的百分比。从图20(a)得到小曲线上传统和径向转向架能达到的扭矩比分别为71%和81%,实际对应的轴重转移分别为5.5%和6.3%,比0.32黏着下的8.8%分别多计入了3.3%和2.5%,得到2种转向架在小曲线上的可用黏着分别为直线上的74.3%和83.5%,径向转向架优势显著,2种转向架与起动时的曲线黏降相比都更严重。
从图20(b)得到大曲线上传统和径向转向架能达到的扭矩比分别为90%和92%,实际对应的轴重转移分别为8.3%和8.5%,比0.32黏着下的8.8%分别多计入了0.5%和0.3%,得到2种转向架在大曲线上的可用黏着分别为直线上的90.5%和92.3%,2种转向架与起动时的曲线黏降相比都更严重。
5.3.4 通过曲线的车轮横向磨耗
原理上转向架通过小半径曲线时依靠车轴横向力导向,通过大半径曲线时依靠蠕滑力导向,因此小半径曲线上外侧轨的车轮易发生轮缘磨耗。
采用不同转向架的前述机车以欠超高、过超高2种不同速度通过曲线,且发挥100%相应速度牵引力时的横向蠕滑率γ2、横向蠕滑力Ty、磨耗指数(Tyγ2值),见表2和表3。结果显示2种转向架都有如下横向磨耗特点:①欠超高通过时,外侧轮的横向磨耗比内侧轮大得多;②过超高通过时,两者趋于均匀;③外侧车轮磨耗点靠向轮缘,内侧车轮磨耗点远离轮缘,即对于钢轨而言外侧轨在轨距角附近产生磨耗,内侧轨在轨顶面产生磨耗;④内侧车轮的横向蠕滑率始终大于外侧车轮,验证了4.1节中的分析结论。虽然特点相同,但径向转向架的磨耗指数显著小于传统转向架,主要与横向蠕滑率的减小有关。2种转向架的运用对比表明,前者的轮缘磨耗和踏面磨耗分别仅为后者的16%和62%[7]。

表2 传统转向架导向轮对横向磨耗数据
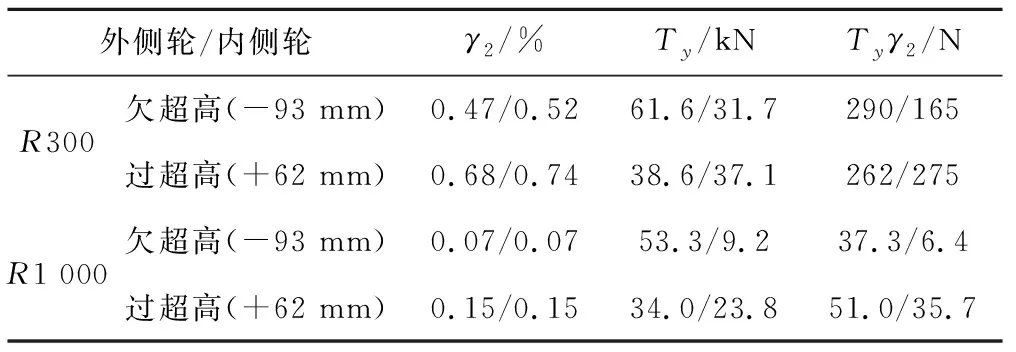
表3 径向转向架导向轮对横向磨耗数据
6 结论
本文提出了33 t轴重内燃机车的总体初步方案和技术参数选择依据,构筑了机车牵引特性、制动特性及总体主要技术参数;基于相同转向架平台和基本动力学参数,提出了三轴传统转向架和三轴径向转向架2种方案。针对所提出机车方案,建立了考虑机车牵引力发挥的多体动力学模型,通过轴重转移计算对模型进行了验证,机车在0.41起动黏着系数下机车轴重转移为11.3%,
从理论上证明了曲线通过时导向轮对内侧车轮冲角始终超过外侧车轮的特点,基于总蠕滑率的考虑提出了适用于所有曲线的机车曲线黏着公式。动力学计算结果表明,径向转向架相比传统转向架在提高机车曲线黏着利用、减小车轮滑动量、减轻机车导向车轮磨耗等方面具有显著优势。

