高中物理中三维运动的降维策略探讨①

陶兆宝 陈新华

(江苏省常州市第一中学，江苏 常州 213003)

1 问题的提出

在高中阶段，学生可以解决二维平面情景下的运动问题，如果将问题设计在三维空间情景下，学生往往会出现思维障碍，不能构建正确的三维空间运动模型，难以利用合适的物理规律和数学空间关系解决问题。所以要引导学生对三维空间中典型运动进行研究，理解其基本分析方法，从而培养学生的分析、解决问题的能力。[1]

2 三维运动的降维策略

2.1 应用数学方法将三维运动问题降至二维运动问题

例1：如图1所示，实心长方体木块长、宽、高分别是a、b、c，且a>c>b，有一个物体沿外表面从A至C1，求物体运动的最短路程。

图1

方法一：利用数形结合方法，将三维问题降至二维。

需要找出可能的运动路径，从A点出发可能由几个平面路径组合而成，将三维问题转化为二维问题，得出共有6种运动路径：ABCD→CC1D1D、ABB1A1→A1B1C1D1、AA1D1D→A1B1C1D1、ABCD→BB1C1C、ABB1A1→BB1C1C、AA1D1D→CC1D1D。

图2

图3

方法二：进行恰当的形体变化，利用平面旋转使三维问题降至二维。

图4

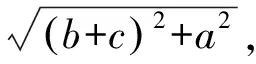
对于三维空间的运动，我们可以通过数学中的解析几何法和平面旋转法进行降维，将三维转化为二维，使研究更为直观简洁，应用数学工具进行有效降维是空间运动研究的基本策略。

2.2 基于运动独立性进行降维，透析三维空间背景下的二维平面问题

例2：如图5所示,正方体上下表面水平，其下表面在水平地面上,正方体的边长为L，将质量为m的小球从顶点A在∠BAD所在范围内(包括边界)分别沿不同的速度水平方向抛出,落点都在A1B1C1D1平面范围内(包括边界)。不计空气阻力，重力加速度为g。若小球轨迹与AC1线段相交，在交点处的速度方向与水平面的夹角为α，求tanα。

图5

将二维平面运动植入三维空间中，有利于学生由浅入深研究物体的空间运动。利用运动的独立性，将三维空间运动按特定方向的单维度独立进行分析，是研究三维空间问题的基本方法。通过这样的研究可以使学生初步掌握三维空间运动的数理关系，强化数学和物理的融合，形成正确的解决立体空间运动的思路，为应用物理规律解决三维复杂运动问题、寻找空间几何关系奠定坚实基础。

2.3 巧用运动的合成和分解方法，构建三维立体空间中的二维平面问题

例3：如图6所示,正方体上、下表面水平,空间有沿A→D方向的匀强电场，从A点沿AB方向分别以初速度v01、v02、v03水平抛出同一带电小球(可视为质点)，小球分别从D1C1的中点、C1点、BC1的中点射出，且射出时的动能分别为Ek1、Ek2、Ek3。不计空气阻力，重力加速度为g，求：

图6

(1) 三次沿AB方向分别抛出时的初速度之比v01∶v02∶v03；

(2) 三次射出时的动能之比Ek1∶Ek2∶Ek3。

解析：(1) 物体的运动性质取决于初速度和所受的外力，根据三次小球落点的位置，由运动的独立性，分别从空间的三个方向分析小球的初速度。小球在AB方向上不受力，沿AB方向做匀速直线运动；小球沿AD方向的初速为零，受到电场力作用，沿AD方向做初速为零的匀加速直线运动；小球沿AA1方向的初速为零，受到重力作用做自由落体运动。由于沿AD、AA1方向的加速度相同，且电场力与重力大小相等，所以加速度大小均为g。

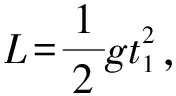
由运动的合成和分解出发，从运动学、动力学角度分析运动关系，将三维问题转化为二维问题，也是重要的问题解决方法。

2.4 利用等效替代方法，将三维立体问题转化为二维平面问题

将三维空间中的速度和受多个力的关系，转化为速度和等效力在二维平面中的关系，这种等效降维方法是将空间多力作用问题简单化的另一个重要思想方法。

2.5 巧用物理规律，将三维问题转化为两点状态关系问题

例3第(2)问与空间运动的功能关系相关，如果用前面的解法，思路与第(1)问类似，解答过程较为繁琐。可根据研究问题的特征，从功能关系入手，将三维立体空间问题转化为起、终两点状态关系问题，则解答过程会简洁、清晰。

物理观念是学生对物理概念和规律理解和应用的提炼升华，让学生形成正确的物理观念，根据物体运动的本质特征，将复杂的空间运动问题转化成状态关系问题，也是解决空间运动问题的重要方法。

3 结语

处理物体在三维空间运动的问题可以用数学方法进行有效降维，也可以通过运动的分解和合成以及力的等效处理进行有效降维，还可以根据物体运动的本质特性进行有效降维。从多种视角综合研判物体的空间运动，将物理、数学方法进行有效融合，可提高学生的综合分析和迁移能力，增强学生的创新意识，有效培养学生的关键能力。